Global tropical cyclone size and intensity reconstruction dataset for 1959–2022 based on IBTrACS and ERA5 data

Tropical cyclones (TCs) are powerful weather systems that can cause extreme disasters. The International Best Track Archive for Climate Stewardship (IBTrACS) dataset provides widely used data to estimate TC climatology. However, it has low data coverage, lacking intensity and outer-size data for more than half of all recorded storms, and is therefore insufficient as a reference for researchers and decision makers. To fill this data gap, we reconstruct a long-term TC dataset by integrating IBTrACS and European Centre for Medium-Range Weather Forecasts Reanalysis 5 (ERA5) data. This reconstructed dataset covers the period 1959–2022, with 3 h temporal resolution. Compared to the IBTrACS dataset, it contains approximately 3–4 times more data points per characteristic. We establish machine learning models to estimate the maximum sustained wind speed (V_max) and radius of maximum wind (R_max) in six basins for which TCs are generated, using ERA5-derived 10 m azimuthal mean azimuthal wind profiles as input, with V_max and R_max data from the IBTrACS dataset used as learning target data. Furthermore, we employ an empirical wind–pressure relationship and six wind profile models to estimate the minimum central pressure (P_min) and outer size of the TCs, respectively. Overall, this high-resolution TC reconstruction dataset demonstrates global consistency with observations, exhibiting mean biases of <1 % for V_max and 3 % for R_max and P_min in almost all basins. The dataset is publicly available from https://doi.org/10.5281/zenodo.13919874 (Xu et al., 2024) and substantially advances our understanding of TC climatology, thereby facilitating risk assessments and defenses against TC-related disasters.

1 Introduction

Tropical cyclones (TCs) are powerful weather systems accompanied by gale winds, heavy rainstorms, substantial waves, and severe storm surges, which cause extensive damage in affected regions (Gray, 1968). During the 2003–2022 period, the global average of TCs is 104 annually, resulting in estimated annual economic losses of USD 95.6 billion and affecting more than 3.2 million individuals (CRED, 2023; Geiger et al., 2018). Given the considerable scale and frequency of TC-related disasters, a comprehensive understanding of TC climatology is essential for effective risk assessment, emergency planning, and community resilience enhancement.

TCs are typically characterized according to their intensity, size, location, and translation speed (Weber et al., 2014). Many studies have reported increasing TC intensity at both the basin and global scale under global warming (e.g., Webster et al., 2005; Gualdi et al., 2008; Wu et al., 2022). Vincent et al. (2014) detect a 30 % increase in high-intensity TCs at the global scale. Mei and Xie (2016) demonstrate a significant correlation between TC intensification and increasing sea surface temperatures (SSTs) in east and southeast Asia. In addition, Walsh et al. (2016) observe significant increasing trends in TC intensity in the Atlantic basin over the past few decades. However, assessments of the response of TC intensity to climate change are subject to uncertainty, partly due to the challenging and costly process of collecting observational data (Gualdi et al., 2008; Knutson et al., 2019). Furthermore, the size of TCs may significantly influence their movement (Liu and Chan, 1999), further contributing to their destructive potential (Xu et al., 2020). Similarly, a significant increase in TC size is proportional to surface latent heat flux under warmer air and ocean temperatures (Hill and Lackmann, 2009; Radu et al., 2014). Xu et al. (2020) demonstrate that TC size increases with ocean warming, based on idealized experiments. Sun et al. (2013, 2014) discover that TC size increases significantly as SST increases through a modeling analysis. However, the conclusions of these case studies are necessarily limited, and the relationships between TC size and climatology factors remain unclear due to the lack of historical records (Xu et al., 2020).

The International Best Track Archive for Climate Stewardship (IBTrACS) dataset is one of the most commonly used sources for TC data; it contains location, intensity, and size data for all known tropical and subtropical cyclones at a resolution of 3 h (Knapp et al., 2010). This dataset utilizes maximum sustained wind speed (V_max) and minimum central pressure (P_min) to quantify TC intensity (Simpson, 1974; Chavas et al., 2017; Casas et al., 2023). Among the several metrics that are defined to measure TC size, one of the most widely recognized is the radius of maximum wind (R_max, Chavas et al., 2015; Ren et al., 2022). Radial distances from the cyclone center to locations where sustained wind speeds of 34, 50, and 64 kn (∼17, 26, and 33 m s⁻¹) are observed near the surface, i.e., R₃₄, R₅₀, and R₆₄, are also widely used metrics to estimate TC size (Pérez-Alarcón et al., 2021). However, reliable TC size and intensity estimates are available only from 1988 onwards (Demuth et al., 2006), and post-storm analyses of wind radii, including R₃₄, R₅₀, and R₆₄, have only commenced since 2004 (Gori et al., 2023). Furthermore, more than half of all recorded storms lack intensity and size data, often with only location data provided, even during periods when post-storm analyses are conducted. Thus, constructing a TC climatology is an arduous task due to low data coverage.

Previous studies have extensively used machine learning to reconstruct TC datasets. Yang et al. (2022) divide hurricane wind fields into symmetric and asymmetric components and propose a downscaling model based on the XGBoost software library to reconstruct TC structure; however, V_max and R_max are the model input variables. Zhuo and Tan (2023) apply deep learning algorithms to estimate reliable TC sizes over the western North Pacific during 1981–2017, based on a homogeneous satellite database. Li et al. (2024) propose a transfer-learning-based generative adversarial network framework to derive TC wind fields from synthetic aperture radar images. Eusebi et al. (2024) demonstrate that a physics-informed neural network can produce accurate reconstructions of TC wind and pressure fields by assimilating observations in a computationally efficient manner. Nevertheless, the datasets used in these studies are generally limited to several cases or specific regions of interest, and some are not publicly available.

By contrast, reanalysis datasets such as the fifth-generation European Centre for Medium-Range Weather Forecasts (ECMWF) Reanalysis 5 (ERA5) dataset (Hersbach et al., 2020), the Japanese 55-year Reanalysis (JRA-55; Kobayashi et al., 2015), and US National Centers for Environmental Prediction and National Centre for Atmospheric Research Reanalysis products (Kistler et al., 2001), which combine past observations and model results through data assimilation, have unique advantages in terms of data availability and spatiotemporal coverage. Schenkel et al. (2017) evaluate whether reanalysis datasets can be used to derive a long-term TC size dataset utilizing QuikSCAT data. Zick and Matyas (2015) explore the impact of satellite-derived precipitation over ocean on TCs in the North American Regional Reanalysis. Gori et al. (2023) use ERA5 reanalysis data to estimate the TCs outer size and a wind model to estimate the radius of maximum wind. Thompson et al. (2024) construct a tropical cyclone (TC) size dataset using the NCEP/NCAR Reanalysis I dataset for landfalling TCs along the US coastline from 1948 to 2022. Previous studies have suggested that ERA5 products are among the most promising reanalysis data sources in terms of representing TC outer size and structure, due to their relatively fine horizontal grid spacing (Bian et al., 2021; Pérez-Alarcón et al., 2021; Dulac et al., 2024). Yeasmin et al. (2023) demonstrate that the reconstruction of TC proxies using ERA5 is a viable approach. Nevertheless, due to horizontal resolution limits and conservative physics parameterizations, reanalysis products have exhibited large underestimation and overestimation of TC V_max and R_max values, respectively (Hatsushika et al., 2006; Schenkel and Hart, 2012). Thus, despite the substantial body of research reconstructing the outer sizes and proxies of TCs using ERA5 data (Bian et al., 2021; Gori et al., 2023; Pérez-Alarcón et al., 2021), studies that have employed it to derive relatively accurate TC intensity data are lacking.

In this study, we exploit the advantages of the IBTrACS and ERA5 datasets to generate a reconstructed TC dataset containing all characteristics of TCs. Given the high degree of accuracy demonstrated by the ERA5 data in capturing TC structures, we employ ERA5-derived azimuthal mean azimuthal wind profiles in conjunction with a machine learning model to reduce the bias observed in the V_max and R_max of TCs between the ERA5 and IBTrACS datasets. In addition, we model six TC radial wind profiles to compute R₃₄, R₅₀, and R₆₄. The resulting long-term TC reconstruction dataset covering the period 1959–2022 is anticipated to facilitate future TC climatology research. The generated dataset is approximately 3–4 times larger than the IBTrACS dataset in terms of the number of records per characteristic.

In the subsequent sections, we describe the IBTrACS and ERA5 datasets and the methodology used to create the novel TC reconstruction dataset. We report and discuss the findings in comparison with IBTrACS data according to a comprehensive set of statistical metrics. Finally, we consider the potential applications of the reconstructed TC dataset.

2 Data

2.1 IBTrACS data

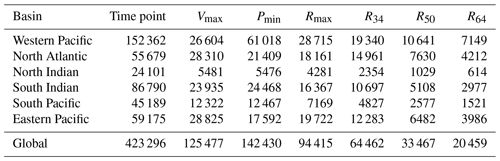
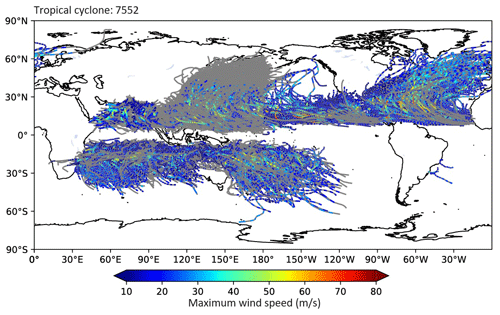
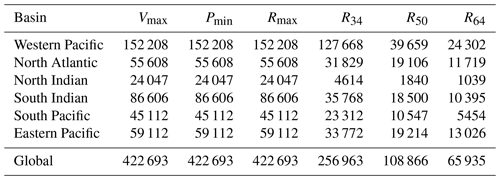
We obtain data on TC tracks, intensity, and size from the IBTrACS (version 4r01 in netCDF format), which is a unified dataset containing track estimates for all TC basins with a 3 h temporal resolution, based on data produced by tropical warning centers. As the TC R_max data from all main TC basins are accessible from US agencies (the National Oceanic and Atmospheric Administration's National Hurricane Center for the North Atlantic and east Pacific and the military's Joint Typhoon Warning Center for the remainder of the globe), we employ these data and exclude the irregular time steps. We use all TC events in all basins, except for those over the South Atlantic, where TC generation is insufficient. A comprehensive overview of the recorded TC characteristics is presented in Table 1. The IBTrACS dataset encompasses a total of 7552 TCs on a global scale, spanning the period 1959–2022, corresponding to 423 296 individual time points. However, IBTrACS only records 125 477 V_max, 142 430 P_min, and 94 415 R_max values. TC tracks and V_max data extracted from the IBTrACS dataset are presented in Fig. 1.

Table 1 Basic information on the number of recorded tropical cyclone characteristics from 1959 to 2022 recorded in IBTrACS.

Figure 1 Overview of the tracks and 10 m maximum wind speeds of tropical cyclones in the IBTrACS dataset. Grey lines represent the unrecorded wind speeds.

2.2 ERA5 data

ERA5 is the latest ECMWF reanalysis, following a decade of developments in model physics, core dynamics, and data assimilation (Hersbach et al., 2020). We utilize the main ERA5 dataset for the period 1959–2022 to estimate the track, intensity, and size of each TC. The spatial resolution of the ERA5 dataset is 0.25°×0.25°, with a temporal resolution of 3 h, aligning with that of the IBTrACS dataset. We exclude pre-1959 ERA5 back-extension data, as some TCs in these data exhibit unrealistically high levels of tension (Bell et al., 2021). Notably, despite the higher uncertainty associated with TC intensity data derived from ERA5 for the pre-satellite time period (1959–1978), comparisons of TC intensity pre- and post-1979 reveal similar climatological distributions for both TC groups in all basins (Fig. S1 in the Supplement). We employ 10 m surface meridional and latitudinal wind speeds to obtain 10 m azimuthal–mean azimuthal wind profiles for TCs. We utilize the sea level pressure (SLP) to provide environmental pressure data for computing the TC central pressure. We derive the parameters including the SLP; relative vorticity at 700, 850, and 925 hPa; and geopotential height at 700 and 850 hPa from the ERA5 data to identify TC centers.

3 Methodology

3.1 TC center identification and azimuthal wind profile estimation

We identify TC centers in the ERA5 data, based on the method of Schenkel et al. (2017). We initially ascertain the position of each TC within the reanalysis grid utilizing the IBTrACS position as a first guess. To remove uncertainties associated with TC centers in the reanalysis data, we obtain the centers of six reanalysis variables (SLP; relative vorticity at 700, 850, and 925 hPa; and geopotential height at 700 and 850 hPa) by calculating the centroids of positive relative vorticity values and negative other variables values over the grid near the first-guess position (±2°) using Python. Subsequently, we average the centers to adjust the position of the estimated reanalysis TC center.

We estimate azimuthal wind profiles based on the ERA5 data, as described by Chavas and Vigh (2014). First, we subtract estimated environment wind fields, which are calculated as 0.55 of the TC translation vectors rotated 20° counterclockwise (Lin and Chavas, 2012) from the meridional and latitudinal wind speeds. We determine TC translation vectors according to the TC positions at the next and current time points in the IBTrACS data. Next, we interpolate the 10 m surface meridional and latitudinal wind fields to a TC-centered polar coordinate. In contrast to the method of Chavas and Vigh, we do not exclude grid points over land to obtain the TC intensity after landfall. Then, we employ the parameter 𝒳, defined as the normalized average magnitude of all vectors from the TC center to each grid point included at a specified radius (Chavas and Vigh, 2014) to remove asymmetrical radial bins by excluding radial bins with 𝒳>0.5. Finally, we calculate the TC 10 m azimuthal–mean azimuthal wind profiles as changes in wind speed with distance from the TC center, with grid points spaced at 10 km intervals. We obtain the ERA5-derived TC V_max (V_{max_ERA5}) and R_max (R_{max_ERA5}) from the wind profiles.

3.2 Machine learning model for reconstructing TC V_max and R_max from ERA5 data

As shown in Fig. 2, there are discernible biases in all six TC basins between the ERA5- and IBTrACS-derived V_max and R_max values. The biases of V_max are less dependent on the basin, suggesting the systematic underestimation of V_max by the ERA5 data, partly due to the lower P_min and the underestimation of the TC wind–pressure relation described in ERA5 (Magnusson et al., 2021). Moreover, convective-scale processes substantially influence V_max, which cannot be adequately represented in global models, leading to an inherent tendency for underestimation. To further demonstrate the performance of ERA5-derived data, we select the Saffir–Simpson categories as the uniform scale for all the basins and analyze the differences between ERA5-derived and observed data across various wind speed ranges, following the methods in previous research (Wright, 2019; Bloemendaal et al., 2020; Mo et al., 2023). In contrast, biases are more pronounced for larger V_max values, with underestimation detected for wind speeds exceeding 20 and 30 m s⁻¹ for Saffir–Simpson categories 1–2 and 3–5, respectively, in all six basins. Notably, this bias even exceeds 40 m s⁻¹ for Saffir–Simpson categories 3–5 in the east Pacific basin. In addition, ERA5-derived results overestimate R_max by >15 km in all basins and by >80 km in the west Pacific (WP) basin. The large biases produced by ERA5 motivate us to establish a reconstructed TC dataset that is more consistent with observations.

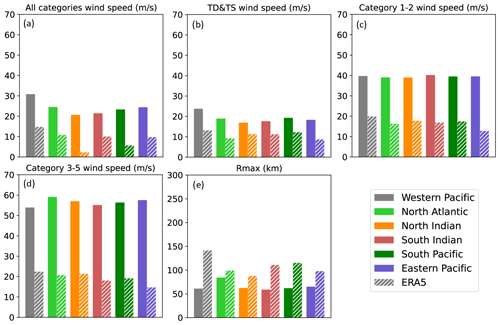
Figure 2 Bar charts for comparing the mean value of the 10 m maximum wind speeds and the radii to maximum winds. Each of the colors indicates a different basin. Solid and dashed bars represent IBTrACS- and ERA5-derived data.

Despite the discrepancy in TC intensity, Bian et al. (2021) demonstrate that ERA-5 accurately depicts TC structural alterations. Therefore, we use the TC 10 m azimuthal-mean wind speed at radial distances from 0 to 1000 km, at 10 km intervals, as a parameter to estimate V_max in each basin. The parameters also include the TC translation speed, given that the IBTrACS V_max data (V_{max_IB}) represent a combination of the environmental and TC wind fields. We optimize the machine learning models by randomized-search cross-validation, with the mean square error as the loss function, using Python. The models include a random forest (RF) algorithm, artificial neural network (ANN), convolutional neural network (CNN), support vector regressor (SVR), and multivariate linear regression (MLR), as detailed in Table 2. In the above-mentioned models, we incorporate data for the entire period (1959–2022) into the model training process. We randomly divide the dataset, made up of the input array and learning target, into two subsets, with 75 % allocated for training and the remaining 25 % for testing, following the methods of previous studies (e.g., Breiman, 2001; Guo et al., 2024). For a detailed account of the hyperparameter selections for each model, please refer to Sect. S1 in the Supplement. We find that RF provided the most robust predictions, as evidenced by higher correlations and smaller root mean square error (RMSE) values in most basins. Accordingly, we develop an RF regressor to predict reconstructed V_max (V_{max_RC}), as follows:

$$\begin{array}{}\text{(1)}& V_{\text{max\_RC}}=\text{RF}(V_{\mathrm{0}},V_{\mathrm{10}},V_{\mathrm{20}},\mathrm{\dots },V_{\mathrm{1000}},V_{\text{TS}}),\end{array}$$

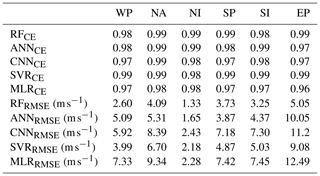
where RF and V_TS are the RF regressor and TC translation speed, respectively, and $V_{\mathrm{0}},V_{\mathrm{10}},V_{\mathrm{20}},\mathrm{\dots },V_{\mathrm{1000}}$ refer to the 10 m azimuthal mean azimuthal wind speeds at radial distances from 0 to 1000 km. To further assess the accuracy of the RF model, we define the error rate of the RF on the training data as the absolute relative errors between the predicted and observed V_max, normalized by the observations. The error rates are 0.11, 0.16, 0.09, 0.19, 0.16 and 0.20 for the WP, North Atlantic (NA), north Indian (NI), south Indian (SI), South Pacific (SP), and eastern Pacific (EP) basins, respectively.

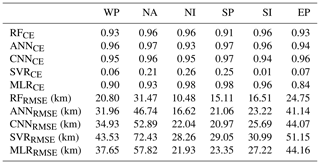
Table 2 Basic information on the comparison of the different model-derived with observed V_max in western Pacific (WP), North Atlantic (NA), north Indian (NI), south Indian (SI), South Pacific (SP) and eastern Pacific (EP). CE, correlation coefficient; RMSE, root mean square error. RF, random forecast; ANN, artificial neural network; CNN, convolutional neural network; SVR, support vector regressor; MLR, multivariate linear regression.

Similarly, we use variation in radial distance with azimuthal wind speed to estimate R_max in the six basins. We also test several machine learning models (Table 3). Although the ANN-derived R_max values exhibit stronger correlations with observations, the RMSE values of R_max derived by RF with observations are considerably smaller than those derived by other models. Therefore, we also utilize the RF regressor to predict the reconstructed R_max (R_{max_RC}), as follows:

$$\begin{array}{}\text{(2)}& R_{\text{max\_RC}}=\text{RF}(R_{\mathrm{0}},R_{\mathrm{0.01}},R_{\mathrm{0.02}},\mathrm{\dots },R_{\mathrm{1}}),\end{array}$$

where $R_{\mathrm{0}},R_{\mathrm{0.01}},R_{\mathrm{0.02}},\mathrm{\dots },R_{\mathrm{1}}$ represent the radial distances at which normalized wind speeds range from 0 to 1, at an interval of 0.01. In the RF models, the error rates are 0.19, 0.23, 0.14, 0.19, 0.15, and 0.23 for the WP, NA, NI, SI, SP, and EP basins, respectively. We further evaluate model performance by comparing the model-derived and observed V_max and R_max on the testing dataset in Sect. 4, using a comprehensive set of statistical metrics, including mean error, mean absolute error (MAE), RMSE, and Pearson correlation coefficients. We evaluate the statistical significance of Pearson correlation coefficients through the application of a t test.

Table 3 Similar to Table 2 but for R_max.

3.3 Empirical wind speed–pressure relationship for determining P_min

We model the conversion between V_max and P_min at a given time point during a TC using the empirical wind–pressure relationship (Atkinson and Holliday, 1977; Harper, 2002), as follows:

$$\begin{array}{}\text{(3)}& V_{\text{max}}=a(P_{\text{env}}-P_{\text{min}}{)}^b,\end{array}$$

where P_env is the environmental pressure obtained from the mean SLP for the TC center location 1–10 d earlier based on the ERA5 data, following the method of Bloemendaal et al. (2020). We estimate a and b in each basin using a nonlinear least-squares approach, based on V_max and the corresponding P_min of the IBTrACS dataset. V_{max_RC} is input into the fitted equation (Eq. 3) to obtain the reconstructed P_min (P_{min_RC}).

3.4 TC radial wind profile models for computing R₃₄, R₅₀, and R₆₄

Previous studies have developed TC radial wind profile models for estimating TC structures (e.g., Pérez-Alarcón et al., 2021). After obtaining the reconstructed V_max and R_max, we utilize six widely used wind field models (Holland, 1980; DeMaria, 1987; Willoughby et al., 2006; Emanuel and Rotunno, 2011; Frisius et al., 2013; Chavas et al., 2015) to estimate the reconstructed TC R₃₄, R₅₀, and R₆₄ (R_{34_RC}, R_{50_RC}, and R_{64_RC}). For a detailed description of the wind profile models, please refer to Sect. S2 in the Supplement.

We evaluate the performance of each profile model by comparing R₃₄, R₅₀, and R₆₄ estimates with those recorded in the IBTrACS dataset. Subsequently, we select the optimal model to generate reconstructed R₃₄, R₅₀, and R₆₄, as described in detail in Sect. 4.

3.5 Flowchart for optimal wind profile model selection

After identifying the TC center, we use an RF approach to estimate V_max and R_max based on the ERA5-derived TC 10 m azimuthal mean azimuthal wind profiles. We evaluate model performance by comparing the model-derived and observed V_max and R_max on the testing dataset, using a comprehensive set of statistical metrics. Next, we estimate the parameters of the empirical wind–pressure relationship and compute TC P_min values. Finally, we derive the TC R₃₄, R₅₀, and R₆₄ by selecting the optimal wind profile model from among the six widely used models. The overall methodology is illustrated in Fig. 3.

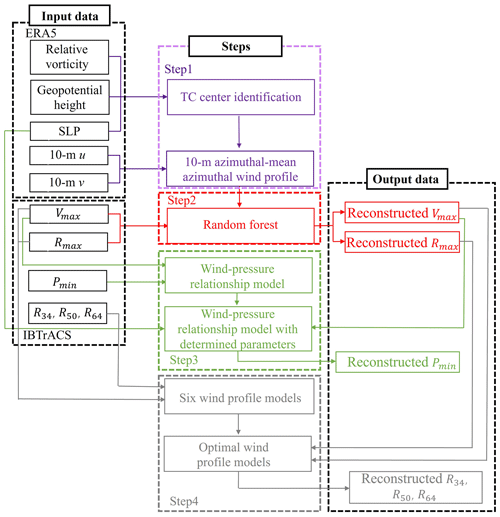
Figure 3 Flowchart with the tropical cyclone center identification and wind profiles extracted from ERA5 (Step 1; in purple), the 10 m maximum wind speeds and radii to maximum winds estimated by the random forest model (Step 2; in red), the minimum central pressure estimated by empirical wind–pressure relationship (Step 3; in green), and the out size estimated by wind profile models (Step 4; in grey).

4 Results and discussion

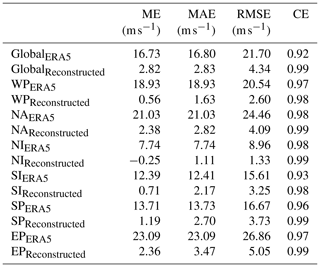
We evaluate the accuracy of the V_{max_RC} model results according to various statistical metrics based on the testing datasets (Fig. 4), as prescribed by Breiman (2001). The V_{max_RC} data are strongly correlated with observations, with correlation coefficients exceeding 0.98 for all six basins. The RMSE values for the WP, NA, NI, SI, SP, and EP basins are 2.60, 4.09, 1.33, 3.25, 3.73, and 5.05 m s⁻¹, respectively. Compared to V_{max_ERA5}, the reconstruction provides a reduction in the MAE of over 10 m s⁻¹ in most basins, with a further reduction of 19.62 m s⁻¹ in the east Pacific basin, as described in detail in Table 4. The model is more effective at reducing biases between ERA5-derived results and observations for larger V_max values. Furthermore, given the high influence of the El Niño–Southern Oscillation (ENSO) on TC intensity (Chu, 2004), we evaluate the accuracy of V_{max_RC} for moderate to strong El Niño and La Niña years (Figs. S2 and S3 in the Supplement). We also observe a high degree of correlation coefficients (>0.97) and low RMSE values (<5 m s⁻¹) between V_{max_RC} and V_max in all six basins during ENSO years. These metrics demonstrate the better accuracy of V_{max_RC} and its reduced bias compared to V_{max_ERA5}.

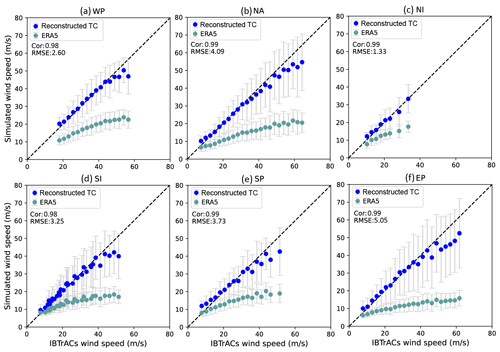
Figure 4 Comparison between value-averaged maximum wind speeds (V_max) from ERA5-derived and reconstructed (ERA5 + random forest) data and IBTrACS maximum wind speeds for tropical cyclones in the (a) western Pacific, (b) North Atlantic, (c) north Indian, (d) south Indian, (e) South Pacific, and (f) eastern Pacific basins. Grey lines represent the error bar, given as 1 standard deviation from the mean. The values with sample sizes less than 30 in IBTrACS are excluded.

Table 4 Basic information on the comparison of the ERA5-derived and reconstructed with observed V_max. ME, mean error; MAE, mean absolute error; RMSE, root mean square error; CE, correlation coefficient.

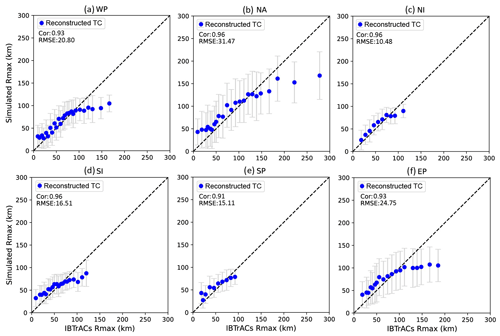
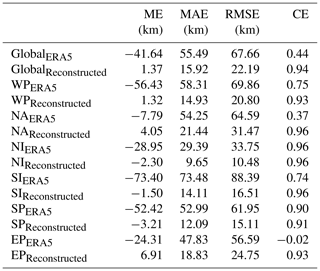
We similarly evaluate the accuracy of R_{max_RC} for the six basins based on the testing datasets (Fig. 5). Correlation coefficients between R_{max_RC} and R_max recorded in IBTrACS (R_{max_IB}) exceed 0.9, indicating strong correlation between the reconstructed results and observations. Moreover, the RMSEs for the WP, NA, NI, SI, SP, and EP basins are 20.80, 31.47 10.48, 16.51, 15.11, and 24.75 km, respectively. Importantly, R_{max_ERA5} exhibits a large deviation from observations, exceeding 300 km at very low R_{max_IB} values. Therefore, for clarity, the R_{max_ERA5} data are not shown with the reconstructed TC results in Fig. 5. The MAE exhibits a reduction of 39.57 km on a global scale, with a further reduction of over 59.37 km in the SI basin, as described in detail in Table 5. It is noteworthy that the error bars are larger for the NA and EP basins in comparison to the other basins. This may be attributed to the low correlations between R_max in IBTrACS and in ERA5 (NA: 0.37; EP: −0.02). Although the R_{max_RC} data slightly overestimate observations at low R_{max_IB} values and underestimate observations at high R_{max_IB} values, they greatly reduce biases compared to the R_{max_ERA5} data and thus produce better predictions for all six basins.

Figure 5 Similar to Fig. 4 but for radii to maximum winds (R_max).

Table 5 Similar to Table 4 but for R_max.

We compute P_{min_RC} based on an empirical wind–pressure relationship. We employ V_{max_IB} and the corresponding P_min recorded in IBTrACS (P_{min_IB}) in the reconstruction, and we obtain P_env from the ERA5 dataset, following the method of Bloemendaal et al. (2020). We estimate related parameters through nonlinear fitting; the results are shown in Fig. 6. For the WP, NA, NI, SI, SP, and EP basins, we use a values of 0.118, 0.051, 0.259, 0.184, 0.325, and 0.073 and b values of 1.67, 1.692, 1.402, 1.507, 1.371, and 1.651, respectively, in Eq. (3).

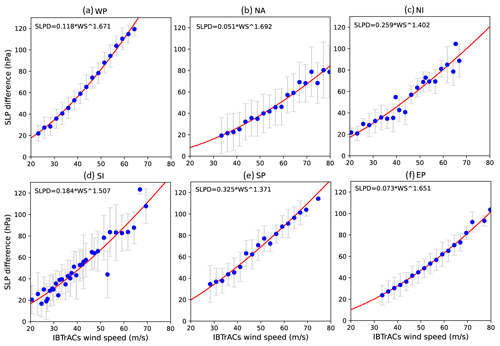
Figure 6 Similar to Fig. 4 but for nonlinear regression analyses between value-averaged IBTrACS maximum wind speeds and the difference between environmental pressure and typical cyclone minimum central pressure (sea level pressure difference, SLPD).

The mean and standard deviation values of various TC characteristics based on the testing datasets are plotted in Fig. 7 to compare the overall performance of the model in reconstructing TCs. Mean biases in R_max and P_min between the reconstructed TC and IBTrACS datasets are both <3 % in most basins, providing compelling evidence that the predictions are in good agreement with observations. In contrast to those over the sea, the reconstructed dataset overestimate and underestimate landfall TC V_max and R_max in most basins, respectively, likely due to the decay of TC wind speeds after landfall, which is not considered in the RF-based models. Despite these differences, biases remain within 5 % in most basins, indicating that the reconstructed landfall TC characteristics are closely aligned with those in the IBTrACS dataset.

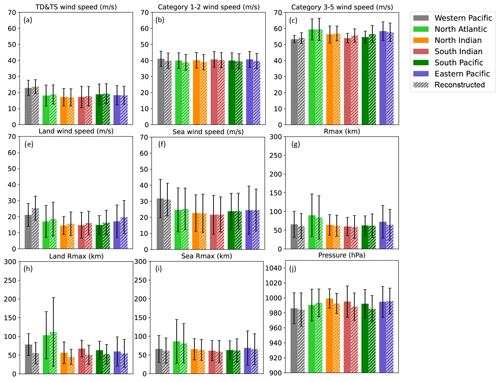
Figure 7 Bar charts for comparing the mean value of the different tropical cyclone characteristics. Each of the colors indicates a different basin. Solid and dashed bars represent IBTrACS and reconstructed tropical cyclone data, respectively.

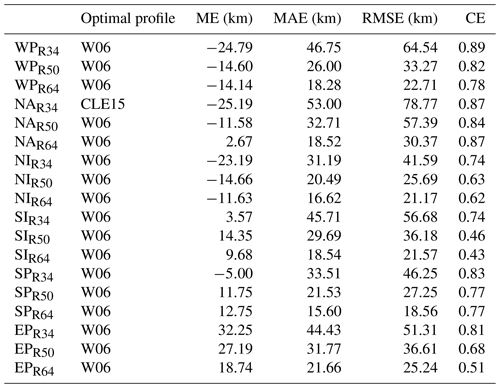
After obtaining the reconstructed TC intensity dataset, we use six widely used models to estimate R_{34_RC}, R_{50_RC}, and R_{64_RC}. We conduct a comparative analysis of the model-derived results and observations to determine which radial wind profile estimate more closely approximated the TC outer radius, based on various statistical metrics (Tables S1–S6 in the Supplement). In the WP basin, the W06 model demonstrates the strongest correlation (R₃₄: 0.89, R₅₀: 0.82, R₆₄: 0.78), achieving the lowest RMSE and MAE. In the NA basin, the CLE15 model outperforms others for R₃₄, with a correlation coefficient of 0.87, RMSE of 78.77 km, and MAE of 53 km, whereas the W06 model performs better for R₅₀ and R₆₄. For the NI and SI basins, all models except W06 show poor correlation with observations, some even exhibiting negative correlations. In the SP and EP basins, W06 substantially surpasses other models in terms of correlation coefficient. Although other models produce slightly smaller RMSE and MAE values for R₆₄ in the EP basin compared to W06, their correlation coefficients, which are <0.2, justify our choice of W06. Consequently, we select W06 to forecast R_{34_RC}, R_{50_RC}, and R_{64_RC} for the WP, NI, SI, SP, and EP basins, whereas for the NA basin, we use CLE15 to predict R_{34_RC} and W06 to predict R_{50_RC} and R_{64_RC}. The correlation coefficients are >0.75 for three outer-size metrics in most basins (Table 6).

Table 6 Basic information on the comparison of the reconstructed data with the observational data for R₃₄, R₅₀, and R₆₄. ME, mean error; MAE, mean absolute error; RMSE, root mean square error; CE, correlation coefficient. H80, D87, W06, E11, F13, and CLE15 refer to the wind field models proposed by Holland (1980), DeMaria (1987), Willoughby et al. (2006), Emanuel and Rotunno (2011), Frisius and Scgönemann (2013), and Chavas et al. (2015).

We use the ERA5 dataset to derive parameters characterizing TC intensity and size in creating the TC reconstruction dataset. Then, we subject these parameters to a machine learning algorithm to produce more accurate data. Notably, we acknowledge that the TC intensity and size reconstructions developed in this study may be influenced by the limitations and uncertainties inherent in the IBTrACS and ERA5 datasets. The RF models are unable to differentiate between landfall and offshore TCs due to the limited data available concerning landfall TCs in the IBTrACS dataset, which results in higher V_max and lower R_max values for landfall TCs. When employing this dataset for the purpose of examining the characteristics and impacts of TCs during their landfall, it is possible to overestimate their intensity while underestimating the scope of their influence. Additionally, we estimate R₃₄, R₅₀, and R₆₄ using wind profile models rather than RF models due to the paucity of relevant data, which results in a lower level of accuracy than for these TC characteristics. Moreover, there is some dependency between the reconstructed and IBTrACS-derived R_max values, likely due to the insufficient spatial resolution of the ERA5 dataset. Finally, TC positions in the IBTrACS data exhibit some degree of inaccuracy during the pre-satellite time period. Therefore, when assessing the impacts of TCs using this dataset, e.g., TC risk assessment, it is crucial to validate the results through observations from meteorological stations, buoys, and other relevant methods. Notwithstanding these limitations, the TC reconstruction dataset exhibits a markedly high degree of accuracy and extensive spatiotemporal coverage. Basic information on the reconstructed TC data is presented in Table 7.

Table 7 Basic information on the number of recorded tropical cyclone characteristics from 1959 to 2022 recorded in reconstructed data.

5 Code and data availability

All data have been published in the form of CSV files and are made publicly available through the Zenodo repository at https://doi.org/10.5281/zenodo.13919874 (Xu et al., 2024). ERA5 data are publicly accessible at https://doi.org/10.24381/cds.bd0915c6 (Hersbach et al., 2023b) and https://doi.org/10.24381/cds.adbb2d47 (Hersbach et al., 2023a). IBTrACS data are accessible at https://doi.org/10.25921/82ty-9e16 (Gahtan et al., 2024). The processing codes can be made available upon request to the corresponding author.

6 Conclusion

The considerable number of unrecorded TC characteristics in the IBTrACS dataset and large biases inherent in the ERA5 dataset prompt us to generate a long-term TC reconstruction dataset. We construct the dataset by integrating TC characteristics from the IBTrACS and ERA5 datasets using RF-based models, an empirical wind–pressure relationship, and six wind profiles for the period 1959–2022. The TC reconstruction dataset is approximately 3–4 times larger than the IBTrACS dataset in terms of data points per characteristic, with much higher data accuracy than shown for ERA5-derived results.

We examine six TC characteristics to evaluate the reconstructed dataset. A comparison of maximum sustained wind speeds between the IBTrACS and reconstructed TC datasets reveals that the latter underestimated observational data by approximately 2.82 m s⁻¹, which is a considerably smaller bias than that shown by the ERA5 dataset (16.73 m s⁻¹) on a global scale. For the radius of maximum wind (R_max), the mean error and RMSE decrease markedly, from −41.64 and 67.66 km (IBTrACS R_max – ERA5 R_max) to 1.37 and 22.19 km (IBTrACS R_max – reconstructed R_max), respectively. In addition, the correlation coefficient for R_max between the IBTrACS and ERA5 datasets is 0.44, which increased to 0.94 between the IBTrACS and TC reconstruction datasets. The mean bias in minimum central pressure between the IBTrACS and reconstructed TC datasets is <3 % in most basins. We use six wind profile models to compute the radii to locations with sustained wind speeds of 34, 50, and 64 kn (i.e., R₃₄, R₅₀, and R₆₄; ∼17, 26, and 33 m s⁻¹), and the selected wind profile models (CLE15 for R₃₄ in the North Atlantic, W06 for others) show good estimates for TC outer sizes, with correlation coefficients >0.75 for three outer-size metrics in most basins. Overall, the TC reconstruction dataset agrees closely with the IBTrACS data in terms of TC intensity and size.

In conclusion, the TC reconstruction dataset may prove invaluable for advancing our understanding of TC climatology, thereby facilitating risk assessments and defenses against TC-related disasters. The future availability of reanalysis data with finer spatial resolution and longer temporal coverage, such as the in-progress ERA6, will facilitate the creation of more accurate TC reconstructions with longer time spans using the methods presented in this study.