Global 1 km land surface parameters for kilometer-scale Earth system modeling

Earth system models (ESMs) are progressively advancing towards the kilometer scale (“k-scale”). However, the surface parameters for land surface models (LSMs) within ESMs running at the k-scale are typically derived from coarse-resolution and outdated datasets. This study aims to develop a new set of global land surface parameters with a resolution of 1 km for multiple years from 2001 to 2020, utilizing the latest and most accurate available datasets. Specifically, the datasets consist of parameters related to land use and land cover, vegetation, soil, and topography. Differences between the newly developed 1 km land surface parameters and conventional parameters emphasize their potential for higher accuracy due to the incorporation of the most advanced and latest data sources. To demonstrate the capability of these new parameters, we conducted 1 km resolution simulations using the E3SM Land Model version 2 (ELM2) over the contiguous United States. Our results demonstrate that land surface parameters contribute to significant spatial heterogeneity in ELM2 simulations of soil moisture, latent heat, emitted longwave radiation, and absorbed shortwave radiation. On average, about 31 % to 54 % of spatial information is lost by upscaling the 1 km ELM2 simulations to a 12 km resolution. Using eXplainable Machine Learning (XML) methods, the influential factors driving the spatial variability and spatial information loss of ELM2 simulations were identified, highlighting the substantial impact of the spatial variability and information loss of various land surface parameters, as well as the mean climate conditions. The comparison against four benchmark datasets indicates that ELM generally performs well in simulating soil moisture and surface energy fluxes. The new land surface parameters are tailored to meet the emerging needs of k-scale LSM and ESM modeling with significant implications for advancing our understanding of water, carbon, and energy cycles under global change. The 1 km land surface parameters are publicly available at https://doi.org/10.5281/zenodo.10815170 (Li et al., 2024).

1 Introduction

Aided by advancements in computing power, it has become increasingly feasible to run land surface models (LSMs) and Earth system models (ESMs) at the kilometer scale (k-scale) to improve our understanding of Earth system processes. The emergence of k-scale modeling has the potential to improve the accuracy of climate simulations significantly and allow for explicit modeling of physical processes that were previously poorly represented in climate models (Change, 2022), such as modeling of mesoscale convective systems in the atmosphere (Slingo et al., 2022) and mesoscale eddies in the ocean (Hewitt et al., 2022). Simultaneously, land modeling has also witnessed a surge of interest in hyper-resolution modeling, initially proposed by Wood et al. (2011), which aims to model land surface processes at a horizontal resolution of 1 km globally and 100 m or finer for continental or regional domains. The motivation behind hyper-resolution modeling is to address the requirements of operational forecasting, like extreme events, and to enhance our understanding of hydrological and biogeochemical cycling and land–atmosphere interactions. High-resolution LSMs have been increasingly applied in various fields, as demonstrated by recent examples, such as the 30 m soil moisture simulations over the contiguous United States (CONUS) (Vergopolan et al., 2020, 2021, 2022), 500 m hyper-resolution modeling of surface and root zone soil moisture over Oklahoma (Rouf et al., 2021), 1 km simulations over southwestern USA (Singh et al., 2015), 3 km simulations over eastern Tibetan Plateau to understand hydrological changes over mountainous regions (Yuan et al., 2018; Ji and Yuan, 2018), and 6 km simulations over China to reduce simulation errors of hydrological variables (Ji et al., 2023). High-resolution modeling can better capture the land surface heterogeneity and could improve simulations of terrestrial water and energy cycles (Giorgi and Avissar, 1997; Chaney et al., 2018; Xu et al., 2023), biogeochemical cycles (Chaney et al., 2018), and land–atmosphere coupling (Liu et al., 2017; Zhou et al., 2019; Bou-Zeid et al., 2020). For example, Singh et al. (2015) demonstrated that increasingly capturing topography and soil texture heterogeneity at finer resolutions (e.g., 1 km) improves land surface modeling of water and energy variables. Li et al. (2022) have shown that the spatial heterogeneities of land surface parameters (including land use and land cover (LULC) and topography) are essential for modeling the spatial variability of land surface energy and water partitioning. Hao et al. (2022) found that 1 km simulations with subgrid topographic configurations can better capture the topographic effects on surface fluxes.

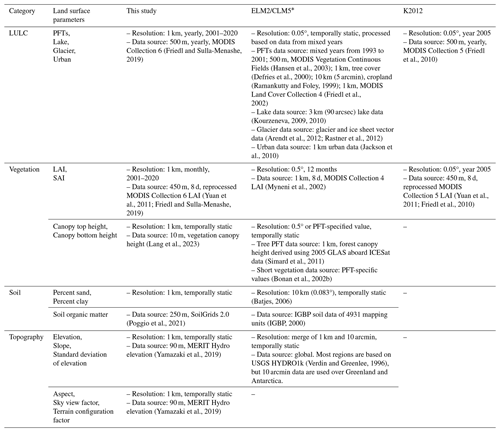
The parameters for LSMs within ESMs being run at the k-scale are typically derived from coarse-resolution datasets or outdated datasets. Consequently, k-scale modeling may not accurately represent fine-scale land surface heterogeneity unless high-resolution land surface parameters at the kilometer or finer scales are utilized. Publicly available land surface parameters are primarily provided at coarse resolutions and based on outdated datasets (see details in Table 1). For example, the Community Land Model version 5 (CLM5; Lawrence et al., 2019) typically relies on land surface parameters with spatial resolutions ranging from 1 km to 0.5° based on source datasets that were processed more than 10 years ago (see Table 1 for details). Although LULC-related parameters are available at a relatively high resolution of 0.05°, they are temporally static and were derived from a combination of data from different years spanning 1993 to 2012 (Table 1). Leaf area index (LAI) was derived from the now outdated products of Moderate Resolution Imaging Spectroradiometer (MODIS) Collection 4 (Myneni et al., 2002). The canopy height for tree plant functional types (PFTs) is based on forest canopy height data derived from the Geoscience Laser Altimeter System (GLAS) aboard ICESat, collected in 2005 (Simard et al., 2011). Canopy height for short vegetation is represented by PFT-specific values that remain invariant in space (Bonan et al., 2002a). Soil sand and clay contents were obtained from the International Geosphere-Biosphere Programme (IGBP) soil dataset (Global Soil Data Task 2000), consisting of 4931 soil mapping units (IGBP, 2000). These CLM5 land surface parameters have been widely utilized in the LSM and ESM communities, despite being developed over a decade ago. Subsequently, Ke et al. (2012; hereafter referred to as K2012) developed an updated set of LULC and vegetation-related land surface parameters for CLM4 at a resolution of 0.05°. These parameters were developed based on MODIS Collection 5 products or datasets derived from MODIS Collection 5 products, including PFTs and non-vegetation land cover, LAI, and stem area index (SAI). The dataset by K2012 has also been widely used by LSMs, including CLM (e.g., Leng et al., 2013; Ke et al., 2013; Singh et al., 2015; Xia et al., 2017) and the Energy Exascale Earth System Model (E3SM) Land Model (ELM) (e.g., Caldwell et al., 2019; Leung et al., 2020; Li et al., 2022). However, the CLM5 and K2012 datasets, with their relatively coarse resolution and reliance on outdated data from over a decade ago, may not fully meet the requirements for k-scale modeling. Additionally, these datasets include LULC, LAI, and SAI data that are year invariant. Consequently, they are inappropriate for studies involving LULC changes, such as urbanization. In addition, some recently developed land surface processes and their associated parameters are not included in previous datasets. For instance, Hao et al. (2022) introduced a subgrid topographic parameterization of solar radiation with five associated topographic factors in ELM, which have been found to significantly affect the surface energy budget.

Table 1 Comparison between new and previous land surface parameters.

^* ELM2 and CLM5 share the same default land surface parameters; detailed are descriptions available at https://escomp.github.io/ctsm-docs/versions/release-clm5.0/html/tech_note/index.html (last access: 6 June 2023; Lawrence et al., 2018).

High-resolution and up-to-date datasets at kilometer or finer resolutions are now widely available and can be utilized to derive more accurate land surface parameters for k-scale LSM simulations. For example, the MODIS Land Cover Type Collection 6 (MCD12Q1, denoted C6) data product provides global land cover types yearly from 2001 to the present (Friedl and Sulla-Menashe, 2019; Sulla-Menashe et al., 2019) at 500 m resolution. Compared to MODIS Collection 4 (used in CLM5 land surface parameters) and Collection 5 products (used in K2012 land surface parameters), the C6 data represent a significant advancement in algorithm improvements and the quality of land cover information. Despite the availability of high-resolution MODIS LAI products, such as the 500 m MCD15A2H (Myneni et al., 2021), they suffer from noise and gaps with spatially and temporally inconsistent values due to clouds, seasonal snow cover, instrument issues, and uncertainties in retrieval algorithms (Yuan et al., 2011). To address these limitations, Yuan et al. (2011) reprocessed MODIS LAI products and generated a more accurate and spatiotemporally continuous and consistent LAI dataset that is available continuously to the present period. Additional high-resolution and up-to-date datasets are available for preparing land surface parameters, such as soil texture and soil organic matter at 250 m resolution (Poggio et al., 2021) and vegetation height at 10 m resolution (Lang et al., 2023).

This study aims to develop a new set of global land surface parameters with a resolution of 1 km for multiple years, utilizing the latest and most accurate datasets. These parameters will be tailored to meet the needs of k-scale Earth system modeling. The newly developed land surface parameters include four categories: (1) LULC-related parameters, such as the spatial distributions of PFTs, lakes, wetlands, urban areas, and glaciers; (2) vegetation-related parameters, including PFTs' LAI and SAI for multiple years ranging from 2001 to 2021, and the canopy top and bottom heights; (3) soil-related parameters, such as soil textures and soil organic matter; and (4) topography-related parameters, such as elevation, slope, aspect, and subgrid topographic factors. We conducted a comparison of the new 1 km parameters against the K2012 and ELM2/CLM5 default parameters. Utilizing ELM version 2 (ELM2) as a test bed, we demonstrated the modeling capability enabled by the new high-resolution parameters through a 5-year simulation at 1 km resolution over CONUS. We performed a spatial scaling analysis on four ELM2-simulated variables, which included soil moisture, latent heat, emitted longwave radiation, and absorbed shortwave radiation, to underscore the significance of high-resolution land surface parameters on ELM2 simulations. We employed eXplainable Machine Learning (XML) methods to evaluate the most important factors of land surface parameters and climate conditions (e.g., mean temperature and precipitation) in driving the spatial variability and spatial information loss of ELM2 simulations.

2 Development of 1 km land surface parameters

In this study, all the land surface parameters were developed globally at a resolution of approximately 1 km (i.e., $\mathrm{1}/\mathrm{120}$°; Table 1). The LULC-related parameters (soil properties, canopy height, and elevation) were processed via Google Earth Engine (GEE; Gorelick et al., 2017). The LAI was processed using an area-weighted average from their original 450 m resolution obtained from Beijing Normal University (Yuan et al., 2011). All data sources utilized in this study have been rigorously validated in their respective original publications. The detailed methods for deriving these parameters are described below.

2.1 LULC-related parameters

In this study, the MODIS MCD12Q1 version 6 (Friedl and Sulla-Menashe, 2019) was employed to ascertain the plant functional types (PFT) as well as other non-vegetative land categories at a spatial resolution of 1 km spanning the years 2001 to 2020. The integrity of the MODIS land cover product has been established through a 10-fold cross-validation accuracy assessment using the Terrestrial Ecosystem Parameterization database (Sulla-Menashe et al., 2019). This land cover product offers richer and more flexible land cover data with higher accuracy and substantially less year-to-year stochastic variation in classification results (Sulla-Menashe et al., 2019). Being the sole operational global land cover product available with annual intervals, it addresses a significant gap in the realm of global change research.

The original MODIS land cover data were first resampled to 1 km from its original 500 m resolution using a majority resampling method in GEE. At such a high 1 km resolution, we did not consider the proportion of different land cover types within each grid. Instead, we assigned 100 % of a grid cell to the major land cover type. Specifically, the MCD12Q1 LC_Type 5 PFT classification layer was used to determine the distributions of the seven PFTs, as well as lake, urban, and glacier, following the method outlined in Ke et al. (2012) and summarized below:

• The seven PFTs include needleleaf evergreen trees, needleleaf deciduous trees, broadleaf evergreen trees, broadleaf deciduous trees, shrub, grass, and crop. These PFTs were further reclassified into 15 categories (Table S1 in the Supplement) that are typically used in LSMs based on the rules presented in Bonan et al. (2002a) with the assistance of 1 km precipitation and surface air temperature from WorldClim V1 (Hijmans et al., 2005).

• Grass was reclassified as C₃ and C₄ grass using the approach presented by Still et al. (2003), with the assistance of monthly LAI (processed in Sect. 2.2.1) and meteorological variables from WorldClim V1.

• The “non-vegetated land” was classified as the barren soil class.

• The “permanent snow and ice” was assigned as the glacier land unit.

• Global lakes were identified based on the classification of “water bodies” over the global land, constrained using the global land mask obtained from Natural Earth (https://www.naturalearthdata.com/, last access: 6 June 2023).

• The urban land unit was determined based on the MODIS “urban and built-up” classification. These urban grids were further classified into three urban classes, namely, tall building district (TBD), high density (HD), and medium density (MD), based on Jackson et al. (2010; hereinafter referred to as J2010). J2010 generated global urban extent maps for the TBD, HD, and MD classes at a spatial resolution of 1 km, based on rules of building height and vegetation coverage fraction (https://gdex.ucar.edu/dataset/188a_oleson/file.html, last access: 6 June 2023). However, the J2010 dataset is temporally static and cannot reflect changes in urban boundaries over time. Therefore, we reclassified the yearly MODIS urban land class as TBD, HD, and MD based on the J2010 dataset using the nearest-neighbor sampling method for each year.

After determining the distribution of 15 PFTs, bare soil, lake, glacier, and urban land, any remaining 1 km grids were assigned as ocean (Table S1). It should be noted that the wetland land unit was not explicitly classified in this study. This is because, instead of treating wetlands as an individual land unit, many LSMs (e.g., ELM2 and CLM5) integrate wetland functioning processes prognostically within other land units where a surface water storage component is implemented to represent wetland functioning.

2.2 Vegetation-related parameters

2.2.1 Monthly LAI and SAI

The monthly LAI parameters were obtained from Beijing Normal University (BNU_LAI; Yuan et al., 2011). BNU_LAI, an enhanced version of the MODIS LAI product, has been subjected to thorough quality control, incorporating multiple algorithms for improved accuracy (Yuan et al., 2011). Its validation involved an extensive array of LAI reference maps and employed the bottom-up approach advocated by the CEOS Land Product Validation Subgroup (Morisette et al., 2006). Compared to the original MODIS LAI, the BNU_LAI dataset exhibits superior performance, along with enhanced spatiotemporal continuity and consistency. The 8 d BNU_LAI product at a resolution of 15 s (∼450 m) over 2001–2020 was downloaded from http://globalchange.bnu.edu.cn/research/laiv061 (last access: 6 June 2023). Subsequently, the data were resampled to a resolution of 1 km using an area-weighted averaging method and averaged temporally for each month. The processed monthly LAI at 1 km resolution was subsequently assigned to each of the 15 PFTs described above at each grid. The monthly SAI was then calculated based on the processed monthly LAI using the methods and PFT parameters described in Zeng et al. (2002).

2.2.2 Vegetation canopy height

We leveraged a global vegetation canopy height dataset sourced from Lang et al. (2023). This dataset, derived using a probabilistic deep learning model, fuses Sentinel-2 images with Global Ecosystem Dynamics Investigation (GEDI) to retrieve canopy height. It stands out as the inaugural global canopy height dataset offering consistent, wall-to-wall coverage at a 10 m spatial resolution across all vegetation types. Assessments using hold-out GEDI reference data and comparisons with independent airborne lidar data demonstrate that the approach outlined by Lang et al. (2023) produces a meticulously quality-controlled, state-of-the-art global map product, accompanied by quantitative uncertainty estimates. The canopy height served as the canopy top height parameter. Canopy bottom height was calculated by multiplying PFT-based ratios derived from the ratio of ELM2's (same as CLM5) canopy top and bottom heights for different PFTs (Table S2).

2.3 Soil-related parameters

We obtained the SoilGrids 2.0 data with an original resolution of 250 m (Poggio et al., 2021) to prepare soil properties. SoilGrids 2.0 is generated using machine learning based on multiple data sources of soil profiles and remote sensing data (Hengl et al., 2017). The soil product underwent rigorous quantitative evaluation using a cross-validation method, which ensures alignment with established pedo-landscape features and provides spatial uncertainty to guide product users (Poggio et al., 2021). SoilGrids 2.0 provides percent clay, percent sand, and soil organic matter for six standard soil layers: 0–5, 5–15, 15–30, 30–60, 60–100, and 100–200 cm. The original SoilGrids 2.0 data obtained from GEE were processed at 1 km resolution with multiple layers using an area-weighted averaging method. To facilitate the demonstration, we restructured the six soil layers vertically into ELM2's 10 effective soil layers (0–1.8, 1.8–4.5, 4.5–9.1, 9.1–16.6, 16.6–28.9, 28.9–49.3, 49.3–82.9, 82.9–138.3, 138.3–229.6, and 229.6–380.2 cm) using the nearest-neighbor method. It should be noted that the lake module in ELM2 and CLM5 requires soil properties, but the SoilGrids 2.0 data may not provide coverage over water surfaces. To address this, we utilized the nearest-neighbor sampling method to map the 1 km soil properties onto the terrestrial water surface.

2.4 Topography-related parameters

We employed the digital elevation from the Multi-Error-Removed Improved-Terrain DEM (MERIT DEM; Yamazaki et al., 2019) to obtain topography-related parameters. The MERIT DEM provides globally consistent elevation data at 90 m resolution, distinguished by its exceptional vertical accuracy. This accuracy was rigorously validated against ICESat's lowest elevations in both forested and non-forested regions and was further benchmarked using the UK's premium airborne lidar DEM (Yamazaki et al., 2019). We first acquired the 1 km elevation and standard deviation of elevation using GEE based on the original 90 m elevation. Further, we calculated the slope, aspect, sky view factor, and terrain configuration factor from the 1 km elevation using the parallel computing tool developed by Dozier (2022). The sky view factor represents the proportion of visible sky limited by adjacent terrain, and the terrain configuration factor describes the proportion of adjacent terrain which is visible to the ground target. Finally, to drive the parameterization of subgrid topographical effects on solar radiation (Hao et al., 2022) in ELM2, we calculated the sin (slope)⋅sin (aspect) and sin (slope)⋅cos (aspect) for calculating the local solar incident angle, as well as two normalized angle-related factors, the sky view factor, and terrain configuration factor by cos (slope). It is important to note that the standard deviation of elevation calculated in this study is specific to the 1 km resolution simulation. For applications requiring coarser resolutions (e.g., 0.5°), the standard deviation should be recalculated directly from the 1 km elevation rather than averaging from the 1 km standard deviation of elevation.

2.5 Comparison between new and existing land surface parameters

In this study, since the data sources used to develop the 1 km global land surface parameters have already undergone rigorous validation, we do not perform additional evaluations against reference datasets (e.g., observations). Instead, our focus is on comparing the newly developed 1 km parameters with those from K2012 and the ELM2/CLM5 default parameters. The K2012 parameters were obtained through personal communication (refer to the “Data availability” section for details). The ELM2/CLM5 default parameters were sourced from the Community Earth System Model (CESM) input data repository (https://svn-ccsm-inputdata.cgd.ucar.edu/trunk/inputdata/, last access: 6 June 2023). Given the different resolutions of these datasets (our new parameters at 1 km, K2012 at 0.05°, and the ELM2/CLM5 defaults with varying resolutions), we adapt our comparison at different resolutions for different variables.

For PFT parameters, we aggregated both the 1 km new parameters and the 0.05° K2012 data to the 0.5° resolution of the ELM2/CLM5 default. For non-vegetated land units (i.e., urban, glacier, and lake), we upscaled the 1 km new parameters to a 0.05° resolution to align with the ELM2/CLM5 default. It is important to note that the urban parameter in K2012 is only available for the Northern Hemisphere, due to limitations in data acquisition.

When comparing LAI, we aggregated the 1 km new and K2012 LAI to 0.5° resolution, matching the ELM2/CLM5 default LAI/SAI resolution. We excluded the comparison of SAI from our analysis due to the limited availability of the global K2012 dataset, from which we only acquired coverage for North America. We have not included a comparison of vegetation canopy height (top and bottom parameters) in our study. This is because the K2012 dataset does not contain these parameters, and the ELM2/CLM5 default parameters in the CESM input data repository provide only tabular values for each PFT rather than spatially variable canopy heights for tree PFTs.

For soil and topography-related parameters, our comparison was limited to the 1 km new parameters and the ELM2/CLM5 default, as K2012 does not include these parameters. Specifically, for soil comparisons, we aggregated the new 1 km parameters to 0.083° resolution to match the ELM2/CLM5 default soil parameters. For topography, given that the ELM2/CLM5 default parameters is a combination of 1 km and 10 arcmin data sources, we simplify the comparison by aggregating both the new 1 km parameters and ELM2/CLM5 default to 0.5° resolution, including elevation and slope.

3 K-scale demonstration simulation over CONUS

3.1 Experiment design

To demonstrate the capability of 1 km datasets, we conducted ELM2 simulations over CONUS at the resolution of 1 km, using the newly developed 1 km land surface parameters for 2010. We used atmospheric forcing from the Global Soil Wetness Project Phase 3 (GSWP3; Kim, 2017) with a spatial resolution of 0.5° to drive ELM. The spatial homogeneity of atmospheric forcings within 0.5° grid cells guarantees that the spatial variability of the ELM-simulated variables (e.g., latent heat) within 0.5° grid cells is solely attributable to the heterogeneity of the 1 km land surface parameters. There are approximately 12 million effective grids over CONUS. We ran ELM for 5 years (2010–2014), and the last year's simulation was used for analysis. We specifically analyzed the annual mean of surface layer soil moisture (SM, m³ m⁻³), latent heat (LH, W m⁻²), emitted longwave radiation (ELR, W m⁻²), and absorbed shortwave radiation (ASR, W m⁻²).

3.2 Spatial scaling analysis

We conducted a spatial scaling analysis following the method described in Vergopolan et al. (2022) on the 1 km ELM simulation data to better understand how k-scale spatial heterogeneity in the four ELM-simulated variables (mentioned in Sect. 3.1) induced only by spatial heterogeneity of land surface parameters changes across spatial scales. First, we performed upscaling by averaging the 1 km ($\mathrm{1}/\mathrm{120}$°) land surface parameters and the four ELM-simulated variables to coarser spatial scales, i.e., λ_scale of $\mathrm{1}/\mathrm{60}$, $\mathrm{1}/\mathrm{40}$, $\mathrm{1}/\mathrm{30}$, $\mathrm{1}/\mathrm{24}$, $\mathrm{1}/\mathrm{20}$, and $\mathrm{1}/\mathrm{10}$°, and we calculated the spatial standard deviation (σ_scale) within each 0.5°×0.5° box at each spatial scale (Table 2). Second, we quantified the changes in spatial variability at different spatial scales compared to the original 1 km resolution by calculating the ratio of σ_scale to σ_1 km. Third, we fitted a $\log \left(\frac{{\mathit{\sigma }}_{\mathrm{scale}}}{{\mathit{\sigma }}_{\mathrm{1}\mathrm{km}}}\right)\propto \mathit{\beta }\times \log \left(\frac{{\mathit{\lambda }}_{\mathrm{scale}}}{{\mathit{\lambda }}_{\mathrm{1}\mathrm{km}}}\right)$ relationship, where β is an indicator to quantify data spatial variability persistence across scales (Hu et al., 1997). A more negative β indicates a larger dependency of data spatial variability on spatial scales, resulting in a higher information loss, denoted as ${\mathit{\gamma }}_{\mathrm{scale}}=(\mathrm{1}-{\mathit{\sigma }}_{\mathrm{scale}}/{\mathit{\sigma }}_{\mathrm{1}\mathrm{km}})\times \mathrm{100}$ %. In this study, we focus on information loss at a 12 km scale, denoted as γ_12 km. For simplicity in the subsequent discussion, γ_12 km will be referred to as γ in the results section. Given the possibility that β may not demonstrate significant temporal variation (Mälicke et al., 2020) and considering that our scaling analysis is intended for demonstration purposes, our spatial scaling analysis is based on the annual mean of ELM2 simulations.

Table 2 Spatial resolution and pixel number at different spatial scales.

It is crucial to clarify that the upscaled 1 km simulation results in the spatial scaling analysis are not equivalent to the results obtained from a coarse-resolution ELM conducted using upscaled parameters. The spatial scaling analysis is intended to emphasize the value of high-resolution modeling in capturing fine-scale spatial variabilities and to highlight the contributions of high-resolution land surface parameters on the simulated variables.

3.3 Attribution analysis utilizing XML methods

We conducted additional analysis to determine the primary land surface parameters that influence the spatial scaling of ELM simulations. We employed XML methods, specifically the eXtreme Gradient Boosting (XGBoost; Chen and Guestrin, 2016) machine learning (ML) algorithm and the game theoretic approach SHapley Additive exPlanations (SHAP; Lundberg and Lee, 2017; Lundberg et al., 2018, 2020). XML methods were utilized to assess the influence of land surface parameters on the spatial variability and information loss of ELM2 simulations across CONUS. Taking spatial variability as an example, we first computed the standard deviation (σ) within each 0.5°×0.5° grid for both 1 km resolution land surface parameters and simulations. Then, we train a machine learning model to predict the spatial variability of each simulated variable (i.e., SM, LH, ELR, ASR). We used the spatial variability (i.e., σ) and mean (μ) of the land surface parameters and μ of precipitation and temperature as predictor variables, and we use the simulated variable's σ as the target variable. After training the machine learning model, we used SHAP to quantify the relative importance and determine which factors were most important in driving the spatial variability of the simulations. Similarly, we used this approach to identify the most critical drivers of information loss.

3.4 Reference datasets for evaluating ELM simulation

We also performed a comparison of all four ELM-simulated variables against reference datasets. It is important to note that we used the default model parameters and did not perform any calibration (see Discussion section for details). For reference datasets, soil moisture was obtained from the Global Land Evaporation Amsterdam Model (GLEAM; Martens et al., 2017), latent heat flux data were from the MODIS product (Running et al., 2021), and both ELR and ASR data were processed from the land component of the fifth generation of the European ReAnalysis (ERA5_Land; Muñoz-Sabater et al., 2021). For the soil moisture evaluation, we compared the surface layer soil moisture from GLEAM (10 cm depth) with the weighted average of the first four-layer soil moisture from ELM (about 11 cm depth). To ensure comparability, we unified the spatial resolution of both reference datasets and ELM simulations to a 0.5° resolution and focused our analysis on the annual mean data for 2014.

4 Results

4.1 Demonstration of the global 1 km land surface parameters

LAI generally shows high values in humid and warm regions, such as tropical rainforests, southeastern USA, and southern Asia, and low values over arid or cold regions, such as central Australia, southwestern USA, the Middle East, central Asia, and northern Canada (Fig. 1a). At high resolution, the LAI dataset clearly reflects the detailed heterogeneity of vegetation distributions. In subregion R1 (Fig. 1b), a relatively small LAI is distributed over mountain ridges and zero LAI over water surfaces (e.g., lakes). In subregion R2 (Fig. 1c), the LAI pattern shows a large proportion of forest fragmentation caused by deforestation. In subregion R3 (Fig. 1d), the LAI shows the distribution of agricultural land along with the river, river mouth, and lakes under an arid climate. R4 shows how urbanization affects vegetation distributions (Fig. 1e).

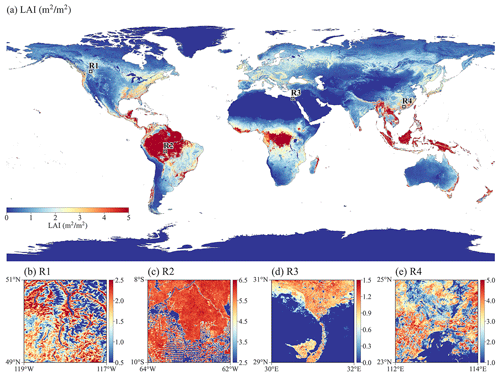
Figure 1 The spatial pattern of LAI (annual mean in 2010) over (a) global land and (b–e) four subregions R1–R4 within 2° boxes marked in (a). Subregions R1–R4 represent topography, deforestation, irrigations, and urbanization effects on LAI.

Figure 2 demonstrates the distribution of plant functional types and other non-vegetation land units. High-resolution LULC types over multiple years can benefit studies related to LULC changes like urbanization and deforestation. Canopy height generally follows a similar spatial pattern with LAI, with high values in humid and warm regions and low values over arid or cold regions (Fig. 3a). The percent clay shows high values over Southeast Asia, India, central Africa, and southeast South America and low content over northern Europe, southern Africa, and Alaska (Fig. 3b). The topography factors follow the elevation patterns (Fig. 3c and d), where there are large slopes and standard deviation of elevation over mountainous regions, such as the Rocky Mountains in North America, the Himalayas in Asia, and the Andes in South America.

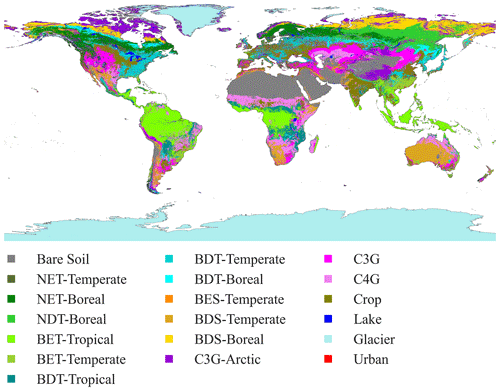
Figure 2 Global LULC distribution in the year 2010. PFT abbreviations include the following: bare soil (Bare Soil); needleleaf evergreen trees in temperate (NET-Temperate) and boreal (NET-Boreal) regions; needleleaf deciduous trees in boreal regions (NDT-Boreal); broadleaf evergreen trees in tropical (BET-Tropical) and temperate (BET-Temperate) regions; broadleaf deciduous trees in tropical (BDT-Tropical), temperate (BDT-Temperate), and boreal (BDT-Boreal) regions; broadleaf evergreen shrubs in temperate regions (BES-Temperate); deciduous shrubs in temperate (BDS-Temperate) and boreal (BDS-Boreal) regions; C₃ grass in arctic (C3G-Arctic) and general (C3G) varieties; C₄ grass (C4G); crops (Crop); lake (Lake); glacier (Glacier); and urban (Urban).

Figure 3 Demonstration of global 1 km datasets (a) canopy top height, (b) percent clay, (c) standard deviation of elevation, and (d) slope.

4.2 Comparison between new and existing land surface parameters

The global distributions of different PFTs show varying degrees of difference when comparing the new parameters with the K2012 and ELM2/CLM5 default parameters (Figs. 4 and S1–S16 in the Supplement). Predominant types such as bare soil, BET-Tropical tree, C₃ and C₄ grasses, and crop are found consistently across all datasets. Notable differences include less bare soil in the new parameters and K2012 compared to the ELM2/CLM5 default, especially in high-latitude North America, western USA, southern Africa, central Asia, and central Australia (Fig. S1). While the new NDT PFT shows larger coverage in Siberia than K2012 and ELM2/CLM5 (Fig. S4), the BET-Tropical PFT is more prevalent in the new parameters across Central and South America (Fig. S5). The BET-Temperate PFT has greater area coverage in southern China in the new parameters (Fig. S6). For BDT-Tropical, BDT-Temperate, and BDT-Boreal PFTs, both the new and ELM2/CLM5 default parameters surpass K2012 data in coverage (Figs. S7–S9). The coverage of the new BDS-Temperate PFT is smaller than K2012 but larger than the ELM2/CLM5 default (Fig. S11), and the new BDS-Boreal PFT is less extensive in the boreal Northern Hemisphere compared to both K2012 and the ELM2/CLM5 defaults (Fig. S12). The C₃-Arctic PFT shows larger areas in the new parameters, particularly in northern Canada, with the new C₄ grass PFT being similar to that of K2012 and larger than ELM2/CLM5 C₄ grass. The crop PFT is less extensive in the new parameters, particularly in southeastern China, Europe, South America, Africa, and Australia.

Figure 4 The global average area fractions of PFTs for three land surface parameter datasets. PFT abbreviations used on the x axis are displayed in Fig. 2.

The global distributions of non-vegetated land covers of lake, glacier, and urban areas vary among the datasets (Figs. S17–S19). The new dataset shows slightly less lake coverage than K2012, but both are smaller than the ELM2/CLM5 default, particularly in high-latitude North America (Fig. S17). Glacier coverage in the new parameter is around 0.7 % smaller than K2012, with noticeable differences in the Arctic North America, while the ELM2/CLM5 default shows more extensive glacier coverage in Antarctica (Fig. S18). Regarding urban areas, K2012 has the smallest urban coverage in the Northern Hemisphere compared to both the new dataset and the ELM2/CLM5 default (Fig. S19). Meanwhile, the ELM2/CLM5 default exhibits more expansive urban areas in India and China than the new dataset and K2012.

The global annual mean LAI exhibits similar spatial patterns among the new parameter, K2012, and ELM2/CLM5 (Fig. 5). The overall global mean LAI for the new parameter (1.28 m² m⁻²) is slightly higher than that of K2012 (1.14 m² m⁻²) and the ELM2/CLM5 default data (1.24 m² m⁻²). In terms of spatial pattern, the new LAI, relative to K2012 (Fig. S20a), shows lower values in the NET-Boreal PFT over the Northern Hemisphere but higher values in the BET-Tropical PFT over the tropics. Similarly, compared with the ELM2/CLM5 default LAI (Fig. S20b), the new LAI also presents smaller values in both the NET-Boreal and NDT PFTs over the Northern Hemisphere but larger values in the BET-Tropical PFT regions.

Figure 5 Comparison of global annual mean LAI for (a) new, (b) K2012, and (c) ELM2/CLM5 default parameters. The global average is indicated in the panel title.

Soil parameters exhibit significant differences between the new and ELM2/CLM5 default datasets (Figs. 6a–c, S21, and S22). The global mean absolute differences between the new and ELM2/CLM5 default for percent sand, percent clay, and organic matter are 14.1 %, 8.1 %, and 30.5 kg m⁻³, respectively. Generally, the new soil parameters are spatially distributed more smoothly than those from ELM2/CLM5 with more patchy patterns (Fig. 6a vs. Fig. 6b). Specifically, the new percent sand is higher in regions like Europe, Siberia, southern Africa, and southern Australia but lower in areas such as the lower Mississippi River basin, northern Africa, and central and southeastern Asia (Fig. 6c). The new percent clay shows larger values in the western USA, northern Africa, central Asia, and Australia but smaller values in Alaska and eastern Europe (Fig. S21). For organic matter, the new parameter indicates smaller values in the Northern Hemisphere but larger values in other global regions compared to the ELM2/CLM5 default (Fig. S22).

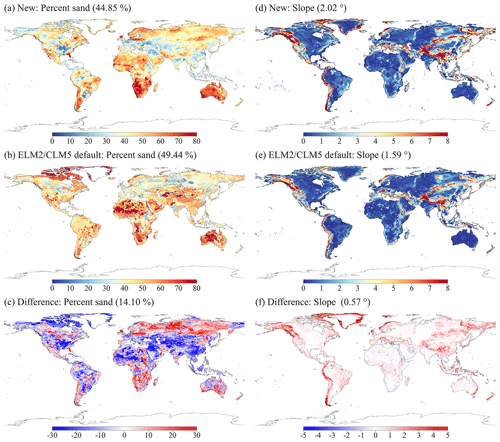
Figure 6 Comparisons of percent sand and slope. (a) New and (b) ELM2/CLM5 default percent sand, along with (c) their difference (new – ELM2/CLM5 default) for percent sand; (d) new, (e) ELM2/CLM5 default, and (f) their difference for slope. The global average is shown in the panel titles, with the global average of the absolute difference provided for (c) and (f).

Topography-related parameters exhibit broadly similar spatial patterns but with notable differences between the new and the ELM2/CLM5 default parameters, as seen in Figs. 6d–f and S23. The new slope parameter generally shows a larger slope relative to the ELM2/CLM5 default, particularly in mountainous regions (Fig. 6f). This could be attributed to the new 1 km slope being calculated from a finer 90 m resolution elevation. Differences in elevation between the new and ELM2/CLM5 parameters are more pronounced in areas such as various mountainous regions, Greenland, the Amazon Basin, the Tibetan Plateau, and Australia (Fig. S23).

4.3 Demonstration 1 km simulation over CONUS

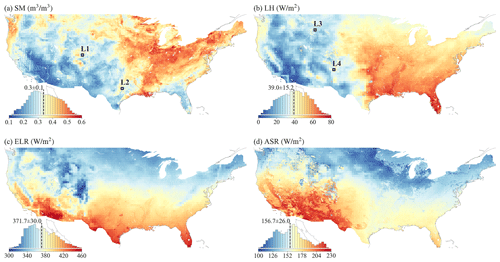
ELM simulations at a 1 km resolution display significant spatial heterogeneity over CONUS (Fig. 7). The values of SM, LH, ELR, and ASR across CONUS follow approximately normal distributions, with averages of 0.3 m³ m⁻³, 39.0, 371.7, and 156.7 W m⁻², respectively (as shown in the histogram plots in Fig. 7). SM shows drier conditions over the west and southwest and wetter conditions over the US Midwest, Corn Belt, Mississippi River basin, and US Northeast (Fig. 7a). LH shows high values over the central and southeast and lower values over the west and southwest (Fig. 7b). The ELR generally shows higher values over regions with high surface temperature in the south (Fig. 7c). The ASR shows higher values over the southwestern regions determined by incoming solar radiation and albedo (Fig. 7d). Despite the high-resolution heterogeneity shown at 1 km resolution, we can still see the spatial patterns distinguished at coarse resolution, i.e., 0.5°×0.5°. These coarser footprints are from the GSWP3 atmospheric forcing with 0.5° resolution. As concluded by Li et al. (2022), atmospheric forcing is one primary heterogeneity source for land surface modeling. Therefore, k-scale atmospheric forcing needs to be developed to further advance k-scale offline land surface modeling.

Figure 7 The annual mean of 1 km simulations of (a) SM, (b) LH, (c) ELR, and (d) ASR over CONUS. The 0.5°×0.5° boxes marked as L1, L2, L3, and L4 in (a) and (b) are selected to demonstrate the spatial scaling analysis. The inserted histogram plot illustrates the distribution of ELM2 simulations.

4.4 Demonstration of spatial scaling across scales

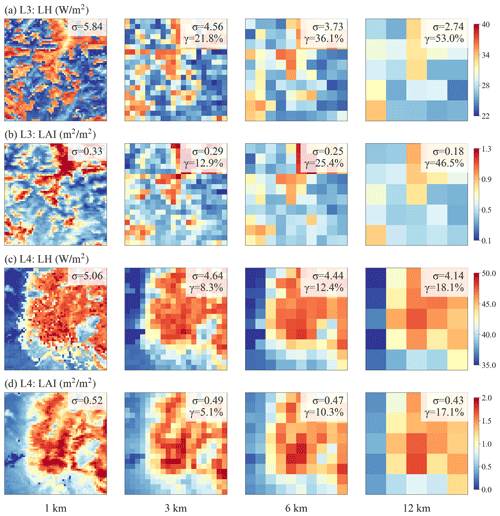
We next demonstrate the relationships between spatial variabilities and spatial scales for SM and LH. Four locations (in Fig. 8a and b) are specifically chosen to showcase varying levels of spatial information loss: L1 and L3 demonstrate a relatively large loss for SM and LH, respectively, while L2 and L4 represent a relatively small loss for SM and LH, respectively.

At location L1 (Fig. 8a), when the 1 km simulation is upscaled to coarser resolutions (i.e., larger spatial scale ratios), the spatial variability of SM decreases, resulting in a negative slope of β. As shown in Fig. 9a, compared to the original 1 km resolution, the information loss γ reaches up to 54.9 % at the 12 km spatial scale. The spatial pattern of SM is consistent with the spatial pattern of percent clay (Fig. 9a vs. Fig. 9b and Fig. 9c vs. Fig. 9d), indicating that soil texture contributes significantly to the spatial variability of SM. However, SM has a more negative β than the percent clay ($\mathit{\beta }=-\mathrm{0.28}$ vs. −0.19 at L1, as shown in Fig. 8a), suggesting that SM variability is amplified likely by other processes that are also influenced by soil texture. In contrast to location L1, location L2 exhibits less negative β values for both SM and percent clay, suggesting that their spatial variabilities exhibit less scale dependence (Figs. 8a and 9c, d). Both SM and percent clay at location L2 approximately maintain their spatial patterns of high values in the west and low values in the east across spatial scales (Fig. 9c and d).

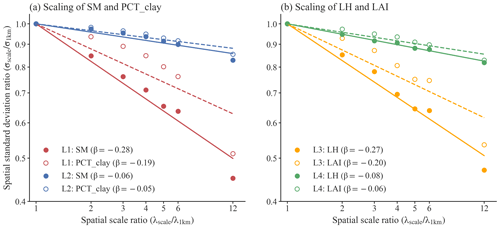
Figure 8 The scaling of spatial variabilities for (a) SM and percent clay and (b) LH and LAI. Both the x axis and y axis are in logarithmic scale. The slope of the linear regression line, β, quantifies the strength of the negative relationship between spatial scale and spatial variability. A more negative β value indicates a higher spatial-scale dependency and increased information loss at coarser spatial scales. Four 0.5°×0.5° boxes (displayed in Fig. 7), namely, L1 to L4, are chosen to contrast larger and smaller negative β values for SM and percent clay (L1 and L2) and for LH and LAI (L3 and L4).

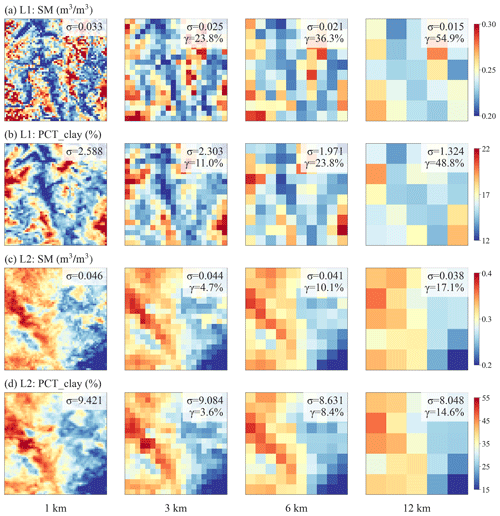
Figure 9 Comparison of SM and percent clay across spatial scales at locations L1 and L2 highlighted in Fig. 7. Each panel displays the spatial patterns of SM or percent clay within a 0.5°×0.5° box, with the σ and γ presented in the legend.

For LH, there is a more negative β value at location L3 than at location L4 ($\mathit{\beta }=-\mathrm{0.27}$ at L3 vs. −0.08 at L4, as shown in Fig. 8b), which indicates a larger decrease of spatial variability across spatial scales and lower variability persistence at location L3 than location L4 (Fig. 10). The spatial pattern of LH is consistent with the spatial pattern of LAI (Fig. 10a vs. Fig. 10b and Fig. 10c vs. Fig. 10d) at different spatial scales, suggesting that vegetation plays a significant role in the spatial variability of LH. Similar to comparison between SM and soil texture, LH has a more negative β than LAI (Fig. 8b).

Figure 10 Similar to Fig. 9, but for LH and LAI at locations L3 and L4.

4.5 The spatial variability of water and energy simulations and their drivers

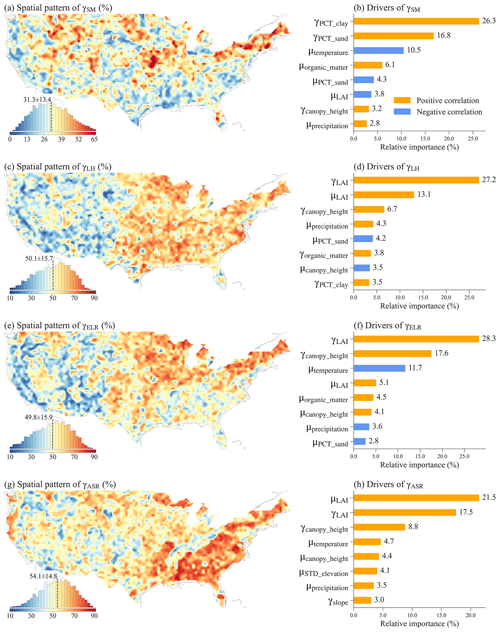
We quantified the spatial variability simulated at 1 km resolution using σ within each 0.5°×0.5° box across CONUS. Four ML models were built to explore the spatial relationships between σ and its potential drivers, including σ of the land surface parameters and the temperature and precipitation averaged over the grid box. Overall, the ML models performed well in predicting the σ of the simulated variables, with small root mean square error (RMSE) and large R² (see Fig. S24). SM shows larger spatial variability in the US Southern Coastal Plain, lower Mississippi River, US Northeast, US Southeast, and regions around the Great Lakes (Fig. 11a), which is roughly consistent with the spatial heterogeneity of the high-resolution SM simulation in Vergopolan et al. (2022). Based on the SHAP method, the spatial variability of SM across CONUS is driven by various factors, mainly including the spatial variabilities of percent sand and percent clay, mean precipitation, the σ and μ of soil organic matter, the σ of canopy height, and mean temperature (Fig. 11b). Mean precipitation and temperature reflect climate conditions (Fig. S26), which are related to the water supply and water demand of soil water content. The spatial heterogeneity of soil properties, such as texture and organic matter content, affects soil hydraulic properties and generate more spatially variable soil water content. Vegetation characteristics, such as canopy height and LAI, could influence SM spatial variability through their effect on roughness length and rooting depth.

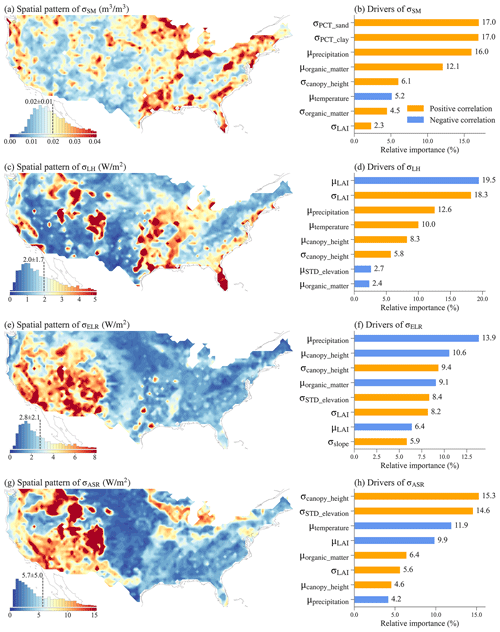
Figure 11 The spatial variability over each 0.5°×0.5° grid cell (a, c, e, g) and the top eight most important drivers (b, d, f, h) of the spatial variability for SM, LH, ELR, and ASR. The inserted histogram plot illustrates the probability distribution of the spatial variability across CONUS. The relative importance of each variable in determining the spatial variability is calculated as the ratio of the mean |SHAP value| of the variable to the sum of the mean |SHAP value| of all variables. Therefore, the sum of the relative importance of all variables is 100 %.

The spatial variability of LH is large in the southeastern, central, and western mountainous regions of the USA (Fig. 11c). Vegetation properties and climate conditions mainly drive the variability of LH (Fig. 11d). The μ and σ of LAI can affect transpiration and soil evaporation, while canopy height can influence surface roughness length and, in turn, evapotranspiration. Mean precipitation and temperature reflect the overall climate conditions related to the water and energy available for latent heat.

ELR and ASR exhibit large spatial variability mainly over the western USA, with ASR additionally showing significant spatial variability across northern USA (Fig. 11e and g). This variability is primarily driven by climate conditions such as mean precipitation and temperature, topographic features such as standard deviation of elevation and slope, and vegetation properties including LAI and canopy height (Fig. 11f and h). These factors are related to the radiation input and surface properties, such as albedo and roughness length, which impact the energy cycles and availability of ELR and ASR.

4.6 The information loss of water and energy simulations and their drivers

We also evaluated the information loss in simulations when upscaling from 1 to 12 km resolution and analyzed the drivers of their spatial patterns over CONUS. Four ML models were built to explore the relationships between the γ of the simulations and its drivers, including the γ of the land surface parameters and the mean temperature and precipitation averaged over the 0.5°×0.5° box. These ML models performed well in predicting the simulations' γ, with small RMSE and large R² (Fig. S25).

Significant information loss ranging from 31 % to 54 % with maximum values exceeding 90 % is observed for SM, LH, ELR, and ASR simulations (Fig. 12). Their spatial patterns and drivers show distinct variations; γ_SM is primarily driven by the information loss of percent clay and sand, mean soil organic matter, and mean temperature, which affects the soil hydraulic properties and soil water balance (Fig. 12a and b). γ_LH displays high values in the eastern USA and low values in the western USA (Fig. 12c). It is primarily contributed by the information loss of vegetation properties such as LAI and canopy height, as well as mean LAI, which influences the partitioning of LH and sensible heat, and the partitioning of transpiration and evaporation (Fig. 12d). γ_ELR exhibits high values in the central and eastern USA, particularly in the northeastern USA, while γ_ASR has high values almost all over the USA, especially in the eastern regions (Fig. 12e and g). γ_ELR and γ_ASR are largely driven by vegetation properties such as LAI and canopy height, which are associated with energy processes such as albedo (Fig. 12f and h). Additionally, topography factors of standard deviation of elevation and slope also slightly contribute to γ_ASR.

Figure 12 Same to Fig. 11 but for information loss.

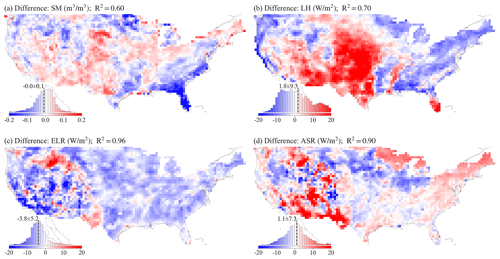
Figure 13 Annual mean bias between ELM-simulated variables and reference datasets over CONUS: (a) SM, (b) LH, (c) ELR, and (d) ASR. The negative values indicate lower ELM values compared to the reference data. The inserted histogram plot illustrates the distribution of grid values. For spatial patterns of the reference datasets, refer to Fig. S27. The correlation coefficient (R²) between the ELM simulation and the reference dataset is calculated and displayed in the title of each panel.

4.7 Comparison of ELM simulation against reference data

The average spatial biases between ELM and reference datasets across CONUS are relatively small, with SM bias at −0.01 m³ m⁻³, LH bias at 1.8 W m⁻², ELR bias at −3.8 W m⁻², and ASR bias at 1.1 W m⁻² (Figs. 13 and S27). The correlation coefficient (R²) between ELM and reference datasets was relatively high at 0.60 (for SM), 0.70 (for LH), 0.96 (for ELR), and 0.90 (for ASR). However, the spatial distribution of these biases exhibits variability, with some areas showing more pronounced biases than others. Specifically, in comparison with GLEAM SM, ELM tends to underestimate SM in the southeastern Texas and across the eastern and southeastern CONUS, while it overestimates SM in the western, central, and southwestern CONUS, including the central-eastern USA, which are primarily agricultural areas. For LH, ELM simulates higher values than the MODIS LH dataset in the western and central USA and Florida but lower values in regions such as the eastern and northeastern CONUS, the western US coastal areas, and the US Pacific Northwest. Regarding radiation variables, ELM generally underestimates ELR across nearly all of CONUS and tends to overestimate ASR, particularly in the southwestern, southern, eastern, northeastern, and northern regions of CONUS.

5 Discussion

The development of new 1 km land surface parameter datasets in this study marks a substantial improvement over commonly used land surface parameters such as CLM5 and K2012, leveraging the latest high-resolution data sources with rigorous validation, including MODIS PFTs, enhanced LAI and canopy height, soil properties, and topography factors. When compared with K2012 and ELM2/CLM5 default datasets, the new 1 km parameters exhibit notable differences, suggesting potential improvement due to the use of more advanced data sources. Distinct features of the new parameters include a reduction in bare soil compared to ELM2/CLM5, especially in regions like North America and Central Asia, and diverse coverage of specific PFTs such as NDT and BET-Tropical in areas like Siberia and South America. The LAI of the new parameters diverges from K2012 and ELM2/CLM5, showing lower values in NET-Boreal PFT of the Northern Hemisphere but higher BET-Tropical PFT in the tropics. The soil parameters, particularly in regions like Europe, Central Asia, and the western USA, show significant differences between the new and the ELM2/CLM5 defaults. Moreover, the new parameters indicate larger slopes in mountainous regions and more distinct elevation differences in areas such as Greenland and the Tibetan Plateau compared to ELM2/CLM5. These differences potentially highlight enhanced accuracy and sophistication of the new 1 km parameters. Their enhanced resolution and rigorous validation suggest a substantial capacity to improve ESM modeling. Additionally, the richness of multi-year data for LULC, LAI, and SAI in these datasets is especially valuable for examining land use and land cover changes, urbanization trends, deforestation impacts, and agricultural transformations.

The new 1 km land surface parameters can improve k-scale offline LSM modeling by better capturing spatial surface heterogeneity. As evidenced by the 1 km ELM simulation over CONUS, soil properties, vegetation properties, and topographic factors contribute a lot to the spatial heterogeneities of ELM water and energy simulations. Upscaling 1 km to a coarser 12 km resolution, we observe significant spatial information loss, with SM experiencing an average loss of 31 %, and LH, ELR, and ASR experiencing around 50 % information loss on average (Fig. 12). This conclusion is in line with the results of Vergopolan et al. (2022), who showed a substantial loss of spatial information in soil moisture when upscaling from 30 m to 1 km resolution, with an average loss of approximately 48 % and up to 80 % over the CONUS region. The XML analysis reveals that the spatial variability and information loss of ELM2 simulations are influenced by the spatial variability and information loss of the different variables of land surface parameters, as well as the mean precipitation and temperature (Figs. 11 and 12). Our findings highlight the critical role of land surface parameters in contributing to the spatial variability of water and energy in land surface simulations, showcasing the value of the developed high-resolution datasets. Another implementation example where our 1 km land surface parameters can be beneficial is in hillslope-scale simulations, which are fundamental for organizing water, energy, and biogeochemical processes (Fan et al., 2019). Krakauer et al. (2014) have highlighted the significance of between-cell groundwater flow, which becomes comparable in magnitude to recharge at grid spacings smaller than 10 km. Advancements have been made in ESMs to address hillslope-scale processes, including the representation of intra-hillslope lateral subsurface flow within grid cells in CLM5 (Swenson et al., 2019), the development of explicit lateral flow processes between grid cells (Qiu et al., 2024), and the incorporation of topographic radiation effects within and between grid cells (Hao et al., 2022). Another notable example is the integrated hydrology-land surface model ParFlow-CLM, which incorporates three-dimensional groundwater flow, two-dimensional overland flow, and land surface exchange processes (Maxwell, 2013). ParFlow-CLM has demonstrated remarkable reliability in reproducing hydrologic processes, such as its simulations at 3 km resolution for pan-European and 1 km resolution for CONUS (Naz et al., 2023; O'Neill et al., 2021). More recently, Fang et al. (2022) coupled ParFlow with ELM and the Functionally Assembled Terrestrial Ecosystem Simulator (FATES) to simulate carbon–hydrology interactions at hillslope scale. By incorporating our 1 km datasets and leveraging these advancements, we can improve simulations of hillslope-scale processes and enhance our understanding of water and energy dynamics within ESMs.

Additionally, the new land surface parameters are also a timely resource for supporting the emerging need for k-scale Earth system modeling, particularly in improving land-atmosphere interaction processes. Representing the impact of spatial heterogeneity on land-atmosphere interaction processes is a major challenge in Earth system modeling. Taking E3SM as an example, researchers have proposed three key approaches to enhance spatial heterogeneity representation to address this challenge. In line with these approaches, our newly developed 1 km land surface parameters offer promising opportunities for improving land-atmosphere coupling within ESMs. The first approach to enhance the representation of spatial heterogeneity is to directly conduct simulations at high resolution. For instance, the Simple Cloud-Resolving E3SM Atmosphere Model (SCREAM) has been used to perform global simulations at 3.25 km (Caldwell et al., 2021), although the land surface parameters were based on coarser-resolution datasets. By utilizing the new 1 km land surface parameters, we can enhance the representation of land surface heterogeneity within the ELM component of SCREAM, potentially improving modeling of land–atmosphere coupling. The second and third approaches focus on improving the representation of land surface heterogeneity within ESMs run at a coarse resolution while accounting for subgrid heterogeneity in two different ways. In the second approach, Cloud Layers Unified By Binormals (CLUBB) has been implemented in E3SM Atmosphere Model (EAM) version 1 (Rasch et al., 2019; Bogenschutz et al., 2013) to better account for subgrid atmospheric heterogeneity of turbulent mixing, shallow convection, and cloud macrophysics. Recently, Huang et al. (2022) developed a novel land-atmosphere coupling scheme in EAM that enables the communication of subgrid land surface heterogeneity information to the atmosphere model with CLUBB, significantly impacting boundary layer dynamics. The new 1 km datasets can provide more accurate land surface representations of the variability of individual patches and the inter-patch variability that were used in Huang et al. (2022). The third approach is the Multiple Atmosphere Multiple Land (MAML) approach used in the multiscale modeling framework (MMF) in which a cloud-resolving model (CRM) is embedded within each grid cell of the atmosphere (Baker et al., 2019; Lin et al., 2023; Lee et al., 2023). In the MAML approach, each CRM column within the atmosphere grid is coupled directly with its own independent land surface. This enables a more explicit representation of the impact of spatial heterogeneity on land-atmosphere interactions within each grid and has shown notable impacts on water and energy simulations (Baker et al., 2019; Lin et al., 2023). Lee et al. (2023) highlighted the limitation of the current MAML approach, which utilizes the same land surface characteristics for each land surface model interacting with the CRM column within the same grid, which could lead to a weak representation of land–atmosphere interactions. To address this limitation, incorporating the new 1 m land surface parameters within the MAML approach can provide more detailed information about land surface heterogeneity, enabling a more accurate capture of land–atmosphere interactions.

Evaluation of k-scale simulations, while essential, faces significant challenges as merely updating the land surface input data to the new 1 km parameters for k-scale simulations does not guarantee improved model performance. This is clearly evidenced in our ELM demonstration simulations, where, despite relatively low CONUS averaged biases for water and energy simulations, the spatial variation in these biases cannot be overlooked, with some regions exhibiting notably larger biases. It is important to emphasize that enhancing model performance requires not just updated input data but also appropriate calibration of model parameters and faithful model structures to represent various processes. First, LSMs and ESMs that have been adapted for simulations at coarser resolutions commensurate with the resolutions of previous land surface data require recalibration for effective high-resolution modeling. This necessity for recalibration is echoed by Ruiz-Vásquez et al. (2023), who noted that updating the ECMWF system with new land surface data did not inherently improve performance, but improvements were seen after recalibrating key soil and vegetation-related parameters. Second, high-resolution modeling requires the incorporation of new physical processes crucial at finer scales. For example, hillslope-scale processes like lateral flow and topography-radiation interactions are key to water and energy fluxes at high resolution (Qiu et al., 2024; Hao et al., 2022). With increased heterogeneity at higher resolutions, larger differences in land surface properties such as vegetation water use strategies requires more attention to plant hydraulics besides the traditional focus on soil hydraulics for a more accurate depiction of plant water use, as highlighted by Li et al. (2021). Third, the lack of high-resolution benchmarks for large-scale applications, like k-scale atmospheric forcing data, remains a challenge, despite the availability of relatively coarse-resolution global datasets such as ERA5_Land (Muñoz-Sabater et al., 2021) and MSWX (Beck et al., 2022). Additionally, using soil moisture as an example, multiple high-resolution datasets exhibit significantly different performance when compared to in situ measurements (Beck et al., 2022). Lastly, when evaluating simulations against benchmarks, it is crucial not only to assess absolute differences using metrics like bias and root mean square error but also to examine other metrics, such as the relationships between physical variables (e.g., rainfall vs. runoff; soil moisture vs. evapotranspiration), information loss, and the tail quantiles of the probability distribution functions for simulations (e.g., extreme events; Li et al., 2020).

There are certain opportunities for future development of 1 km parameters. The urban extension may vary based on data sources, urban definitions, and the algorithms employed, such as those derived from harmonized nighttime lights (Zhao et al., 2022), global artificial impervious area (GAIA; Li et al., 2020b; Gong et al., 2020), and urban expansion (Liu et al., 2020; Kuang et al., 2021), necessitating careful consideration in specific modeling applications. Additionally, urban classification in J2010, based on global building height data, is limited by the lack of a consistent and publicly accessible global dataset, despite available regional data for Europe (Frantz et al., 2021), the USA (Li et al., 2020a), and China (Cao and Huang, 2021; Yang and Zhao, 2022), thus posing challenges to future urban classification enhancements. Incorporating local climate zones offers a promising approach for urban classification and modeling (Huang et al., 2023). Moreover, the multiple-year high-resolution PFT maps like the ones developed by the European Space Agency's Climate Change Initiative could be used to further extend this dataset for a longer period (Harper et al., 2023). Soil color, crucial for soil albedo and surface energy balance, lacks extensive global datasets for ESM modeling, but the global soil color map derived by Rizzo et al. (2023) offers potential for further kilometer-scale ESM and LSM modeling.

The strategic aggregation of high-resolution parameters to coarser resolutions is crucial to maintain accuracy and effectiveness in modeling applications. For instance, in soil properties, the basic parameters (e.g., percent sand) are often utilized to derive secondary parameters (e.g., saturated water content). This aggregation procedure, whether performed before or after deriving secondary parameters – known as “aggregating first” and “aggregating after” – is influenced by the nonlinear relationships between basic and derived parameters, with the latter method generally preferred (Shangguan et al., 2014; Dai et al., 2019). Our study's initial approach in upscaling soil- and topography-related parameters follows the aggregate first approach, aligning with the structure of models like ELM2 and CLM5. Conversely, models such as Common Land Model (CoLM; Dai et al., 2003) and community Noah with multi-parameterization options (Noah-MP; He et al., 2023; Niu et al., 2011; Yang et al., 2011) integrate secondary derived soil related parameters directly as inputs, effectively demonstrating the advantages of the aggregating after approach. By leveraging secondary derived parameters from comprehensive databases such as SoilGrids (Hengl et al., 2017) and GSDE (Shangguan et al., 2014), these models provide a valuable framework for future development of models like ELM2 and CLM5 by directly integrating secondary derived parameters.

6 Data availability

The 1 km land surface parameters are publicly available at Zenodo: https://doi.org/10.5281/zenodo.10815170 (Li et al., 2024).

7 Conclusions

We developed 1 km global land surface parameters using the latest available datasets covering multiple years from 2001 to 2020. These parameters comprise four categories: LULC of PFTs and non-vegetative land cover, vegetation properties, soil properties, and topographic factors. The new 1 km parameters, when compared to the K2012 and ELM2/CLM5 default datasets, display significant differences, indicating their potential superiority stemming from the utilization of the latest and more advanced data sources. The 1 km resolution ELM simulations conducted over CONUS demonstrate the valuable capabilities of the new datasets in enabling k-scale land surface modeling. Through scaling analysis of the 1 km resolution simulations within 0.5°×0.5° boxes where spatial heterogeneity of the simulations is induced only by spatial heterogeneity of the land surface parameters, we revealed the significant impact of land surface parameters on the spatial variability of water and energy simulations. The spatial information loss of these simulations over CONUS is significant when upscaling from 1 km to a coarser 12 km resolution, with an average ranging from 31 % to 54 % and up to more than 90 %. The XML analysis reveals that the spatial variability and spatial information loss of ELM2 simulations are primarily impacted by the spatial variability and information loss of soil properties, vegetation properties, and topography factors, as well as the mean climate conditions of precipitation and temperature. Furthermore, the spatial variability of water and energy in the 1 km simulations is not dominated by the spatial heterogeneity of any land surface parameters, suggesting the usefulness of the multi-parameter high-resolution land surface parameter dataset. Furthermore, the comparison against four benchmark datasets indicates that ELM generally performs well in simulating soil moisture and surface energy fluxes. The availability of 1 km land surface parameters is a valuable resource that addresses the emerging needs of k-scale LSM and ESM modeling. By providing accurate and precise information, these 1 km land surface parameters will significantly enhance our understanding of the water, carbon, and energy cycles under global change.