A global map of root biomass across the world's forests

As a key component of the Earth system, roots play a key role in linking Earth's lithosphere, hydrosphere, biosphere and atmosphere. Here we combine 10 307 field measurements of forest root biomass worldwide with global observations of forest structure, climatic conditions, topography, land management and soil characteristics to derive a spatially explicit global high-resolution (∼ 1 km) root biomass dataset, including fine and coarse roots. In total, 142 ± 25 (95 % CI) Pg of live dry-matter biomass is stored belowground, representing a global average root : shoot biomass ratio of 0.25 ± 0.10. Earlier studies (Jackson et al., 1997; Robinson, 2007; Saugier et al., 2001) are 44 %–226 % larger than our estimations of the total root biomass in tropical, temperate and boreal forests. The total global forest root biomass from a recent estimate (Spawn et al., 2020) is 24 % larger than this study. The smaller estimation from this study is attributable to the updated forest area, spatially explicit aboveground biomass density used to predict the patterns of root biomass, new root measurements and the upscaling methodology. We show specifically that the root shoot allometry is one underlying driver that has led to methodological overestimation of root biomass in previous estimations. Raw datasets and global maps generated in this study are deposited at the open-access repository Figshare (https://doi.org/10.6084/m9.figshare.12199637.v1; Huang et al., 2020).

1 Introduction

Roots act as a hub that connects complex feedbacks among biomes, soil, water, air, rocks and nutrients. Roots mediate nutrient and water uptake by plants, belowground organic carbon decomposition, the flow of carbohydrates to mycorrhizae, species competition, soil stabilization and plant resistance to windfall (Warren et al., 2015). The global distribution of root biomass is related to how much photosynthate plants must invest belowground to obtain water, nitrogen and phosphorus for sustaining photosynthesis, leaf area and growth. Root biomass and activity also control the land surface energy budget through plant transpiration (Wang et al., 2016; Warren et al., 2015). While Earth observation data combined with field data enable the derivation of spatially explicit estimates of aboveground biomass with a spatial resolution of up to 30 m over the whole globe (Santoro, 2018b), the global carbon stock and spatial details of the distribution of belowground root biomass (fine + coarse) have so far relied on sparse measurements and coarse extrapolation, thus remaining highly uncertain.

More than 20 years ago, Jackson et al. (1996, 1997) provided estimates of the average biomass density (weight per unit area) and vertical distribution of roots for 10 terrestrial biomes. Multiplying their average root biomass density with the area of each biome results in a global root biomass pool of 292 Pg, with forests accounting for ∼ 68 %. Saugier et al. (2001) estimated global root biomass to be 320 Pg by multiplying biome average root to shoot ratios (R:S) by shoot biomass density and the land area of each biome. Mokany et al. (2006) argued that the use of mean R:S values at the biome scale is a source of error because root biomass measurements are performed at small scales but root distributions are highly spatially heterogeneous and their size distribution spans several orders of magnitude, with fine roots being particularly difficult to sample (Jackson et al., 1996; Taylor et al., 2013). With an updated R:S and broader vegetation classes, Mokany et al. (2006) gave a higher global root biomass of 482 Pg. Robinson (2007) further suggested that R:S was underestimated by 60 %, which translated into an even higher global root biomass of 540–560 Pg. These studies provided a first-order estimation of the root biomass for different biomes but not of its spatial details. Further, it is worth noting that estimations of the total global root biomass have increased with time, likely associated with improved methods in excavating roots that reduce under-sampling.

An alternative approach to estimating root biomass is through allometric scaling, dating back to West et al. (1997, 1999) and Enquist and Niklas (2002). The allometric scaling theory assumes that biological attributes scale with body mass, and in the case of roots, an allometric equation verified by data takes the form of R∝S^β, where R is the root mass, S the shoot mass and β a scaling exponent. In contrast to the studies listed above that assume the R:S ratio to be uniform, this equation implies that the R:S ratio varies with shoot size when β is not equal to 1 (Cairns et al., 1997; Enquist and Niklas, 2002; Jiang and Wang, 2017; McCarthy and Enquist, 2007; Niklas, 2005; Robinson, 2004; Zens and Webb, 2002). Allometric equations also predict that smaller trees generally have a larger R:S with β<1, which is well supported by measurement of trees of different sizes (Cairns et al., 1997; Jiang and Wang, 2017; Niklas, 2005; Robinson, 2004; Zens and Webb, 2002). The allometric equation approach was applied to various forest types, and the scaling exponent β was observed to differ across sites (Luo et al., 2018); species (Cheng and Niklas, 2007); age (Cairns et al., 1997); leaf characteristics (Luo et al., 2012); elevation (Moser et al., 2011); management status (Ledo et al., 2018); and climatic conditions, such as temperature (Reich et al., 2014), soil moisture and climatic water deficit (Ledo et al., 2018), as well as soil nutrient content and texture (Jiang and Wang, 2017). Despite the successful application of allometric equations to site- and species-specific studies (Luo et al., 2018), their use to predict global root biomass patterns appears to be limited and challenging.

2 Methods

2.1 Overview

We use a new approach to upscale root biomass of trees at the global scale (Supplement, Fig. S1) based on machine learning algorithms trained by a large dataset of in situ measurements (n=10 307) of root and shoot biomass for individual woody plants (see Methods, “Field measurements”; Supplement), covering 465 species across 10 biomes defined by The Nature Conservancy (Olson and Dinerstein, 2002) (Supplement, Fig. S2). We compared the results of allometric upscaling to those of three machine learning techniques (the random forest, artificial neural networks and multiple adaptive regression splines), through a pool of 47 predictor variables that include shoot biomass and other vegetation, edaphic, topographic, anthropogenic and climatic variables (Supplement, Table S1). After comparing the results of all three machine learning techniques and the allometric upscaling, we chose the random forest (RF) model because it performed best on cross-validation samples (see section “Building predictive models” below and Supplement, Table S8), and we only used the RF for subsequent mapping and analysis. Using this RF model, we mapped the root biomass of an average tree over an area of ∼ 1 km × 1 km across the globe using as predictors gridded maps of shoot biomass (weight per area) (Santoro et al., 2021, 2018), tree height (Simard et al., 2011), soil nitrogen (Wang et al., 2014), pH (Wang et al., 2014), bulk density (Wang et al., 2014), clay content (Wang et al., 2014), sand content (Wang et al., 2014), base saturation (Wang et al., 2014), cation exchange capacity (Wang et al., 2014), water vapor pressure (Fick and Hijmans, 2017), mean annual precipitation (Fick and Hijmans, 2017), mean annual temperature (Fick and Hijmans, 2017), aridity (Trabucco and Zomer, 2019) and water table depth (Fan et al., 2013) (Supplement, Figs. S10–S12). Combining our map of root biomass per tree with the tree density (number of trees per area) (Crowther et al., 2015b) at the global scale, we quantified the global forest root biomass.

2.2 Field measurements

Our dataset (Huang et al., 2020) was compiled from the literature and existing forest biomass structure or allometry databases (Falster et al., 2015; Ledo et al., 2018; Schepaschenko et al., 2018, 2017). We included studies and databases that reported georeferenced location, root biomass and shoot biomass. Note here that we focus on studies that measured biomass of individual trees instead of stand-level biomass. We included studies that measured biomass directly, instead of those that estimated it indirectly via allometric equations. For example, the study of Poorter et al. (2015) is not included due to lack of georeferenced location and the study of Iversen et al. (2017) is not used as we also need measurements of other plant compartments like shoot biomass. Repeated entries from existing databases were removed. One of the databases (Falster et al., 2015) reported data on woody plants which also include shrub species. We kept the shrub data partly because the remote sensing products we used to generate our root map do not clearly separate trees from shrubs. Around 82 % of the extracted entries also recorded plant height and management status. Height was identified as an important predictor in our model assessment, and entries were discarded when height was missing (18 % of data). As woody plant age was reported in 19 % of the entries only, the values of this variable were determined from another source of information, i.e., from a composite global map introduced in the next section. Species names were systematically reported, but biotic, climatic, topographic and soil information was missing for a substantial proportion of entries, and values of these variables were thus extracted from independent observation-driven global maps as explained in the next section. Our final dataset includes biomass measurements collected in 494 different locations from 10 307 individual plants, which cover 465 species across 10 biomes as defined by The Nature Conservancy (Olson and Dinerstein, 2002) (Supplement, Fig. S2).

2.3 Preparing predictor variables

We used 47 predictors that broadly cover five categories: vegetative, edaphic, climatic, topographic and anthropogenic (Supplement, Table S1). These variables are chosen due to their relevance to root dynamics based on field studies and their availability at the global scale. Vegetative variables include shoot biomass, height, age, maximum rooting depth, biome class and species. Edaphic predictors cover soil bulk density, organic carbon, pH, sand content, clay content, total nitrogen, total phosphorus, Bray phosphorus, total potassium, exchangeable aluminum, cation exchange capacity, base saturation (BS), soil moisture and water table depth (WT). Climatic predictors are mean annual temperature (MAT), mean annual precipitation (MAP), the aridity index that represents the ratio between precipitation and the reference evapotranspiration, solar radiation, potential evapotranspiration (PET), vapor pressure, cumulative water deficit (CWD = PET − MAP), wind speed, mean diurnal range of temperature (BIO2, BIO is the abbreviation for WorldClim bioclimatic indicators), isothermality (BIO2 $/$ BIO7) (BIO3), temperature seasonality (BIO4), max temperature of the warmest month (BIO5), min temperature of the coldest month (BIO6), temperature annual range (BIO7), mean temperature of the wettest quarter (BIO8), mean temperature of the driest quarter (BIO9), mean temperature of the warmest quarter (BIO10), mean temperature of the coldest quarter (BIO11), precipitation of the wettest month (BIO13), precipitation of the driest month (BIO14), precipitation seasonality (BIO15), precipitation of the wettest quarter (BIO16), precipitation of the driest quarter (BIO17), precipitation of the warmest quarter (BIO18), and precipitation of the coldest quarter (BIO19). The topographic variable is elevation. We take the management status (managed or not) as the anthropogenic predictor. All references are given in the Supplement, Table S1. For each variable, we collected multiple datasets whenever possible for uncertainty quantification. For the “central” estimate, we stick to only one set of these predictors considering the quality and coverage of the databases. We favored the database that is known to have higher-quality data or covered more predictors that are relevant to our study for consistency. For example, we used the GSDE soil database (Wang et al., 2014) for the central estimate instead of SoilGrids 2.0 (Poggio et al., 2021) as the latter does not have the whole set of soil property variables needed in this study.

As in situ field measurements of aboveground biomass (AGB) do not offer a full global coverage, gridded shoot biomass data were derived from satellite AGB products to predict root biomass at the global scale with a 1 km by 1 km spatial resolution. The gridded global shoot biomass dataset used in our study has been extensively calibrated with in situ observations and is currently the most reliable source of information on shoot biomass offering global coverage (Santoro et al., 2021, 2018; Spawn et al., 2020). To derive the shoot or AGB per tree (in units of weight per tree) to generate spatially explicit global root biomass, we combined the GlobBiomass AGB satellite data product (Santoro et al., 2021, 2018) (in units of weight per unit area) with a tree density map (number of trees per unit area) (Crowther et al., 2015b). The GlobBiomass dataset was based on multiple remote sensing products (radar, optical, lidar) and a large pool of in situ observations of forest variables (Santoro et al., 2015, 2021; Santoro, 2018). The original GlobBiomass AGB map was generated at a 100 m spatial resolution; for this study, the map was averaged into a 1 km pixel by considering only those pixels that were labeled as forest (Santoro, 2018). A pixel was labeled as forest when the tree canopy density was larger than 15 % according to the dataset of Hansen et al. (2013; hereafter Hansen2013) averaged at 100 m. The 1 km resolution global tree density map was constructed through upscaling 429 775 ground-based tree density measurements with a predictive regression model for forests in each biome (Crowther et al., 2015b). The forest canopy height map took advantage of the Geoscience Laser Altimeter System (GLAS) aboard ICESat (Ice, Cloud, and land Elevation Satellite) (Simard et al., 2011). Forest definitions are slightly different among these three maps. Forest area of the tree density map was based on a global consensus land cover dataset that merged four land cover products (Tuanmu and Jetz, 2014). Crowther et al. (2015b) showed the total tree count from a tree density map based on the Tuanmu and Jetz (2014) land cover is the same as from the Hansen2013 land cover product. The canopy height map used the GlobCover land cover map (Hagolle et al., 2005) as a reference to define forest land. We approximated the missing values in tree density and height (due to mismatches in forest cover) by the mean of a 5×5 window that is centered on the corresponding pixel. We quantified the potential impact of mismatches in the forest definition by looking into two different thresholds: 0 % and 30 %.

We merged several regional age maps to generate a global forest age map. The base age map was derived from biomass through the age–biomass curve similarly to the method conducted in tropical regions in Poulter et al. (2019). This age map does not cover the northern region beyond 35^∘ N. We filled in the missing northern region with a North American age map (Pan et al., 2011) and a second age map covering China (Zhang et al., 2017). The North American age map represents the year around 2003, and as a coarse approximation, we added 7 years to represent the year 2010. The China age map was derived for the period 2009–2013. We took it to approximate age values in China around 2010. Remaining missing pixels were further filled with the age map derived from MODIS disturbance observations. For the final step, we filled the remaining pixels with the GFAD V1.1 age map (Poulter et al., 2019). GFAD V1.1 has 15 age classes and 4 plant functional types (PFTs). GFAD V1.1 represents the 2000–2010 era. As a coarse approximation, we chose the middle value of each age class and estimated the age as the average among different PFTs.

Detailed information of all ancillary variables is listed in the Supplement, Table S1. To stay coherent, we re-gridded each map to a common 1 km × 1 km grid through the nearest-neighborhood method.

2.4 Building predictive models

We investigated the performance of the allometric scaling and three non-parametric models: the random forest (RF), artificial neural networks (ANNs) and multiple adaptive regression splines (MARSs). Allometric upscaling relates root biomass to shoot biomass in the form of R∝S^β. We assume that one universal allometric equation (Enquist and Niklas, 2002) governs biomass partitioning across species without stratifying the data by species. RF is an ensemble machine learning method that builds a number of decision trees through training samples (Breiman, 2001). A decision tree is a flow-chart-like structure, where each internal (non-leaf) node denotes a binary test on a predictor variable, each branch represents the outcome of a test and each leaf (or terminal) node holds a predicted target variable. With a combination of learning trees (models), RF generally increases the overall prediction performance and reduces over-fitting. An ANN computes through an interconnected group of nodes, inspired by a simplification of neurons in a brain. A MARS is a non-parametric regression method that builds multiple linear regression models across a range of predictors.

Tree shoot biomass from the in situ observation data spans a wider range than shoot biomass per plant derived from global maps ($\mathrm{1}\times {\mathrm{10}}^{-\mathrm{7}}$ to 8800 vs. $\mathrm{7.9}\times {\mathrm{10}}^{-\mathrm{5}}$ to 933 kg/plant). To reduce potential mapping errors, we selected training samples with shoot biomass between $\mathrm{5}\times {\mathrm{10}}^{-\mathrm{5}}$ and 1000 kg/plant. The medians and means of shoot biomass, root biomass and R:S from the selected training samples are similar to those from the entire database. Also, to reduce the potential impact of outliers, we analyzed samples with R:S falling between the 1st and 99th percentiles, which consist of 9589 samples with R:S ranging from 0.05 to 2.47 and a mean of 0.47 and a median of 0.36. Sample filtering slightly deteriorated model performance and had a minor impact on the final global root biomass prediction (145 from whole samples vs. 142 Pg from filtered data). We chose root biomass as our target variable instead of R:S because big and small trees contribute equally to R:S, while big trees are relatively more important in biomass quantification. In our observation database, we have more samples that are small woody plants (Supplement, Fig. S6). We furthermore split the in situ-measured shoot biomass into three groups, namely measurements with shoot biomass smaller than 0.1, between 0.1 and 10, and larger than 10 kg/plant, and trained a specific model for each class. The rationale behind this splitting is (1) to remove the bias of small plants from the distribution of in situ-measured woody shoot biomass (Supplement, Fig. S6), (2) to account for the shift of root shoot allometry with tree size (Poorter et al., 2015; Ledo et al., 2018; Zens and Webb, 2002), (3) to improve the performance of independent validation through numerous combinations of splitting trials, and (4) because tests through weighting samples or resampling samples (e.g., over-sampling using the synthetic minority over-sampling technique) showed no better performance.

Model performances were assessed by 4-fold cross-validation using two criteria: the mean absolute error (MAE) and the R-squared value (R²). MAE quantifies the overall error, while R² estimates the proportion of variance in root biomass that is captured by the predictive model. We favored the model with the smallest MAE and the highest R². For models with comparable MAE and R², we favored the model with the minimum number of predictors. For non-parametric models, starting from a model with all 47 predictors, we sequentially excluded predictors that did not improve model performance one after another. The order of removing predictors was random. After a combination of trials, the best model was from RF (Supplement, Table S8) and the final set of predictors included shoot biomass, height, soil nitrogen, pH, bulk density, clay content, sand content, base saturation, cation exchange capacity, vapor pressure, mean annual precipitation, mean annual temperature, aridity and water table depth. Note the maximum rooting depth had a minor impact on model performance and was not selected in the final model. The depth to which roots inhabit soil varies among species and environment. Our model predictions are therefore not specific to a certain soil depth.

2.5 Generation of the global root biomass map

Over an area of 1 km × 1 km, we assumed a tree with an average shoot biomass follows the RF model trained above. Building upon a large set of samples with each field measurement being an outcome of complex local interactions (including within-vegetation competition), we implicitly accounted for some sub-pixel variability (e.g., resource competition and responses to environmental conditions) in root biomass. Our RF model was built upon individual woody trees. We combined the RF model with global maps of selected predictor variables to produce the map of root biomass for an average woody tree which has a unit of weight per tree. This map was multiplied by tree density (number of woody trees per area) (Crowther et al., 2015a) at a 1 km resolution to obtain the final root biomass map with a unit of weight per area (Supplement, Fig. S1).

2.6 Uncertainty quantification

We estimated the overall uncertainty in the root biomass estimates through quantifying errors caused by predicting root biomass at the 1 km resolution (η_pred) and converting root biomass per tree to root biomass per unit area (η_con). We quantified the prediction uncertainty through an ensemble of predictions. We collected eight additional global predictor datasets (three shoot biomass, two soil and three climate datasets) (Supplement, Table S2) and carried out 8×4 (4 folds) sets of additional predictions replacing the predictors by each of these additional data maps. We calculated the standard deviation among 36 predictions for each pixel (Supplement, Fig. S4a). Converting root biomass from per tree to per area is performed through the tree density (Crowther et al., 2015b). We assumed the coefficient of variation (CV, i.e., the ratio of the standard deviation to the mean) in tree density mapping caused the same relative uncertainty in our per-unit-area root biomass. The CV in tree density mapping at the biome scale was derived from Crowther et al. (2015b) through dividing uncertainties in quantifying total tree numbers by the total tree numbers. η_con in terms of standard deviation is therefore equal to the product of CV and the mean root biomass at each pixel (Supplement, Fig. S4b). At last we propagated these two sources of uncertainty assuming these errors were random and independent. Note that we did not account for uncertainties in in situ root biomass measurements used in training the RF model. The overall uncertainty (standard deviation) at the pixel level was calculated through

$$\begin{array}{}\text{(1)}& {\mathit{\eta }}_{\mathrm{root}}=\sqrt{{\mathit{\eta }}_{\mathrm{pred}}^{\mathrm{2}}+{\mathit{\eta }}_{\mathrm{con}}^{\mathrm{2}}}.\end{array}$$

At the biome and global scales, we obtained total root biomass for each of the 36 predictions and estimated the standard deviations of the total root biomass. η_con was estimated by multiplying the CV by biome- or global-level root biomass. We propagated these two sources of uncertainty through Eq. (1). Note that the semivariogram of the random forest prediction errors does not show a clear autocorrelation pattern (Supplement, Fig. S10).

2.7 Relative importance of predictor variables

The impact of predictors on predicting R:S was estimated through Spearman's rank-order correlation at both the global and the biome scales. We log-transformed the R:S and shoot biomass before standardizing these datasets. Partial dependence plots (Hastie et al., 2009) show the marginal effect that one predictor has on root biomass from a machine learning model and serves as a supplement to the Spearman correlation.

3 Results

We estimated a total global root biomass of 142±25 (95 % CI) Pg (see Methods for uncertainty estimation and the Supplement, Figs. S3 and S4) for forests when forest is defined as all areas with tree cover larger than 15 % from the Hansen et al. (2013) tree cover map. Note here that we reported values in units of petagrams of dry biomass instead of petagrams of C. The corresponding global weighted mean R:S is 0.25 ± 0.10. The root biomass spatial distribution generally follows the pattern of shoot biomass, but there are significant local and regional deviations as shown by Fig. 1. Of the global tree root biomass, 51 % comes from tropical moist forest; 14 % from boreal forest; 12 % from temperate broadleaf forest; and 10 % from woody plants in tropical and subtropical grasslands, savanna, and shrublands (Supplement, Table S3). Given our use of a tree cover threshold of 15 % at a 100 m resolution, our estimate ignores the roots of isolated woody plants present in arid or cold regions (Staver et al., 2011), as well as heterogeneous (e.g., urban or agriculture) landscapes and is possibly an underestimate. Total root biomass decreases from 151 to 134 Pg when the canopy cover threshold used to define forest land is increased from 0 % to 30 %. The root biomass density per unit of forest area is the highest in tropical moist forest, followed by temperate coniferous and Mediterranean forest (Fig. 1; Supplement, Table S3). Cross-validation showed a good match between predictions from our RF model and in situ observations (Fig. 2e, all data; Supplement, Fig. S7, for each biome; Supplement, Fig. S8, for three tree size classes; Supplement, Fig. S9, for each continent), with an overall coefficient of determination R² of 0.85, a mean absolute error (MAE) of 2.18 kg and a median R:S similar to validation samples (0.35 from in situ observation vs. 0.38 from prediction). RF shows better performance than the other two machine learning algorithms and the allometric fitting, as shown in the Supplement, Table S8. By continents, the performance of RF is worst in Africa (R²=0.6; MAE = 44 kg) partly due to limited observations (Supplement, Fig. S9). Root biomass of tropical, temperate and boreal forests together from earlier studies is 44 %–226 % higher than in this study (Tables 1, S5; see Supplement, “Comparison with published results”).

Table 1 Comparison between studies quantifying root biomass in tropical, temperate and boreal forests.

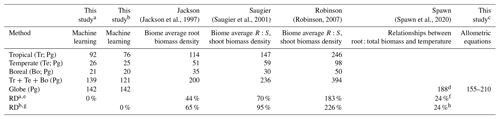
^a Tropical moist forest (Biome 1), tropical dry forest (Biome 6), tropical/subtropical coniferous forest (Biome 11) and forest in tropical/subtropical grasslands/savannas and shrublands (Biome 3) are aggregated to represent tropical systems (Tr). Temperate broadleaf/mixed forest (Biome 4), temperate coniferous forest (Biome 5) and forest in temperate grasslands/savannas and shrublands (Biome 8) are merged together as temperate systems (Te). Boreal forest (Biome 2) and woody plants in tundra regions (Biome 7) are aggregated as boreal forest (Bo). Biome classification is from The Nature Conservancy (Olson and Dinerstein, 2002) and is shown in the Supplement, Fig. S2. ^b Tropical systems (Tr): biomes 1, 6, 11; temperate systems (Te): biomes 4, 5; boreal systems (Bo): Biome 2. ^c Estimation based on allometric equations and the global aboveground biomass dataset from Santoro et al. (2021) and Santoro (2018). See the Supplement, Table S7, for details. ^d This value is converted from 94 Pg C to 188 Pg of biomass assuming a 50 % carbon content of tree biomass. ^e RD^a, the relative difference in Tr + Te + Bo between this study (^a) and previous quantifications. RD^a= (previous study − this study) $/$ this study ×100 %. For example, in the column with the heading Jackson, RD${}^{\mathrm{a}}=(\mathrm{200}-\mathrm{139})/\mathrm{139}\times \mathrm{100}$ % = 44 %. ^f,h Relative to our machine learning estimate with 0 % tree cover threshold as the forest definition, i.e., 151 Pg of root biomass globally. ^g RD^b, the same as RD^a but with the ^b definition of tropical, temperate and boreal systems.

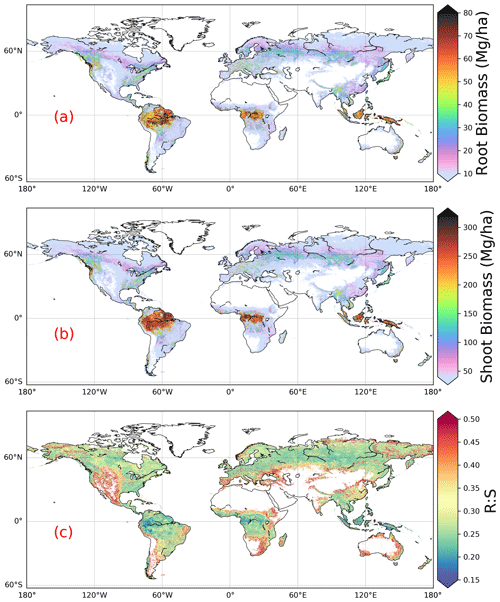
Figure 1 Global maps of forest root biomass generated through the random forest model (a), shoot biomass from GlobBiomass AGB (Santoro et al., 2021; Santoro, 2018) (b) and R:S (c). Forest is defined as an area with canopy cover > 15 % from the Hansen et al. (2013) tree cover map.

Figure 2 Root biomass and root shoot ratio (R:S). Panels (a) and (b) show as violin plots the distribution of root and shoot biomass (in units of kilograms per plant) and R:S ratios in the raw data used for upscaling. Panels (c) and (d) are the distributions of model-predicted root biomass from this study, aboveground biomass used for the prediction, and modeled R:S ratios at the global and biome scales. Panel (e) is a heat plot of observed vs. predicted root biomass in kilograms of root per individual woody plant (see the Supplement, Figs. 7–9, for cross-validation at biome, tree size class and continental scales). Panel (f) shows the mean (purple) and median (grey) R:S as a function of shoot biomass from observations. A shift of the shoot biomass towards a larger size (a, c) results in a smaller predicted mean R:S at the global scale (b, d) (see the Supplement, Table S4, for exact values) as the mean R:S is size dependent. R² is the coefficient of determination; MAE is the mean absolute error; and N is the number of samples. TropMoist: tropical moist forest; Boreal: boreal forest/taiga; TempBroad: temperate broadleaf and mixed forest; TempConif: temperate coniferous forest; Mediterran: Mediterranean forests, woodlands and scrub; TropConif: tropical and subtropical coniferous forest; and Mangrove: mangrove forest. Note that the scales of the y axes are different between (a) and (c) and between (b) and (d). Model training and prediction were conducted on filtered data with R:S falling between the 1st and 99th percentiles and shoot biomass matching the range derived from GlobBiomass AGB (Santoro et al., 2021; Santoro, 2018) to reduce impacts from outliers.

We then analyzed the dominant factors explaining spatial variations in root biomass and R:S (see Methods). Broadly speaking, locations with small trees, low precipitation, strong aridity, deep water table depth, high acidity, low bulk density, low base saturation and low cation exchange capacity are more likely to have higher fractional root biomass (Fig. 3). In line with the allometric theory, shoot biomass emerged as the most important predictor of R:S and root biomass, as given by the Spearman correlation analysis shown in Fig. 3 and partial importance plots (Supplement, Figs. S11–S13). Water-related variables (precipitation, water table depth, aridity and vapor pressure) also emerged as important predictors in explaining R:S patterns (Fig. 3) (Ledo et al., 2018), with trees and woody plants in dry regions generally having higher R:S (Supplement, Tables S3 and S4) and with stronger dependence on precipitation especially when precipitation is low and on water table depth when the water table is deep. Temperature is slightly negatively correlated with R:S at the global scale, in line with Reich et al. (2014). However, the relationship between temperature and belowground biomass is not consistent among biomes (Fig. 3) and biomass size groups (Supplement, Figs. S11–S13).

Figure 3 Spearman rank correlations between predictor variables and log-transferred R:S. Spearman coefficients are shown at both the global and the biome scales for LogAGB, the logarithm of shoot biomass with base 10; HEIGHT, plant height; MAT, mean annual temperature; MAP, mean annual precipitation; WT, water table depth; ARIDITY, the aridity index; VAPR, water vapor pressure; N, soil nitrogen content; BD, soil bulk density; BS, soil base saturation; CEC, soil cation exchange capacity; CLAY, soil clay content; SAND, soil sand content; and pH, soil pH. From left to right, biomes are ordered by decreasing forest areas (Supplement, Fig. S2).

The relationship between total soil nitrogen and root biomass is negative when soil nitrogen content is below 0.1 %–0.2 % (Supplement, Figs. S11–S13). Root biomass and R:S generally increase with soil alkalinity (Figs. 3, S11–S13). Low pH is toxic to biological activities and roots, especially as fine roots are sensitive to soil acidification, as revealed by a recent meta-analysis (Meng et al., 2019). Our results also indicate overall positive correlations between CEC, BS and R:S, but the processes that may account for these correlations are less clear from the literature. Age has been shown to be important for R:S (Schepaschenko et al., 2018). How age regulates R:S remains elusive, with studies showing both a positive (Waring and Powers, 2017) and a slightly negative (Mokany et al., 2006) relationship between R:S and age. Including forest age (see Methods, “Preparing predictor variables”) as a predictor only marginally improved our model prediction (see the Supplement for details). It is likely that shoot biomass partially accounts for age information, and the quality of the global forest age data might also affect the power of this variable in improving root biomass predictions.

4 Data availability

Raw datasets and global maps generated in this study are deposited at the open-access repository Figshare (https://doi.org/10.6084/m9.figshare.12199637.v1; Huang et al., 2020). The source data and code underlying Figs. 1–3 and S2–S17 are also provided at Figshare.

5 Code availability

Calculations were conducted through Python 2.7.15 and Ferret 6.72. The code is deposited at the open-access repository Figshare (https://doi.org/10.6084/m9.figshare.12199637.v1; Huang et al., 2020).

6 Discussion

Our lower estimation of root biomass compared to earlier studies is attributable to differences in forest area (Supplement, Table S5), aboveground biomass density (Supplement, Table S5), root biomass measurement and upscaling methodology. For example, the forest area in temperate zones used in Jackson et al. (1997) was about one-third higher than in this study. Using the root biomass density (Supplement, Table S5) and estimation method from Jackson et al. (1997) but the updated forest area map from this study, we estimated total root biomass of tropical, temperate and boreal forests to be 147 Pg (or 184 Pg if sparse forests in tropical/subtropical/temperate grasslands/savannas and shrublands and tundra regions are accounted for, S1 biome definition in Table 1). This value is smaller than the 200 Pg from Jackson et al. (1997) but still larger than the 121 Pg (or 139 Pg) (Table 1) from our machine learning approach. Our lower values of root biomass compared to Saugier et al. (2001), Mokany et al. (2006) and Robinson (2007) are caused mainly by our lower aboveground biomass density and R:S (Supplement, Table S5). Shoot or aboveground biomass (AGB) density of tropical zones is 70 % lower in our study than in Robinson (2007), who used sparse plot data collected more than a decade ago (Supplement, Table S5, case S2), and this lower AGB explains 27 %–46 % of our lower root biomass (Supplement, Tables S5 and S6). On the other hand, lower biome average R:S explains 41 %–48 % of our underestimation compared to Robinson (2007). To elucidate this difference, we calculated weighted biome average R:S ratios through dividing total biome-level shoot biomass by root biomass (i.e., weighted mean R:S). These weighted mean R:S values, ranging between 0.19 and 0.31 across biomes (Supplement, Table S3), are generally smaller than the R:S values reported in previous studies, which were based on average ratios obtained from sparser data (Supplement, Table S5). Note that the arithmetic mean R:S values (without weighting by biomass) from woody plants located in tropical, temperate and boreal zones (Supplement, Table S4) from our database are close to those from Robinson (2007) (Supplement, Table S5). And our predicted patterns of relatively large R:S in regions such as dry forests, savannas and boreal tundra woodlands (Fig. 1c) are in line with data compiled from Mokany et al. (2006) and the 2019 IPCC refinement (IPCC, 2019). Spawn et al. (2020) estimated root biomass from shoot biomass and the correlation between root : total biomass and temperature. Among previous studies, the recent study from Spawn et al. (2020) shows the smallest difference from our study. Compared to our estimation with the 0 % tree cover threshold for forest definition (i.e., 151 Pg of root biomass), the 24 % higher estimation from Spawn et al. (2020) is most likely linked to the upscaling methodology, in addition to the slight difference in the definition of forest (woody) area especially in Africa and tundra.

The common practice of estimating root biomass through an average R:S without considering the spatial variability in biomass and this ratio is a source of systematic error, leading to overestimating the global root biomass for two reasons. Firstly, upscaling ratios through arithmetic averages (possibly weighted by the number of trees or area but not accounting for the fine-grained distribution of biomass) systematically overestimates the true mean R:S because R:S is a convex negative function of S given by $R:S\propto S^{\mathit{\beta }-\mathrm{1}}$, with β taking typical values of about 0.9 (Mokany et al., 2006; West et al., 1997, 1999) (see also the Supplement, “Arithmetic mean R:S” section). This explains why high-resolution S data used to diagnose weighted mean R:S ratios in our approach give generally smaller values than using arithmetic means across grid cells at the biome level (Weighted R:S Ratio in the Supplement, Table S3, vs. Mean (Gridded) in the Supplement, Table S4). Multiplying this biome-level arithmetic mean R:S by the average biome-level shoot biomass (Supplement, Table S3) yielded a global forest root biomass of 155 Pg, larger than 142 Pg. Secondly, available measurements tend to sample more small woody plants than big trees compared to real-world distributions because small plants are easier to excavate for measuring roots (see Fig. 2a, c), but smaller plants tend to have larger R:S (Fig. 2e; see also Enquist and Niklas, 2002, and Zens and Webb, 2002). This sampling bias shifts the R:S towards larger values. If we use the biome-level mean R:S from our in situ database (Mean (Obs) in the Supplement, Table S4), multiplying the shoot biomass (Supplement, Table S3) yields a global value of 233 Pg, larger than using the mean R:S across grid cells through RF (155 Pg). Our RF approach uses in situ data for training, but in the upscaling, it accounts for realistic distributions of plant size (Supplement, Fig. S5; Supplement, Table S4). We further verified that our upscaled R:S ratios are robust to sub-sampling the training data in observed distributions so that the bias of training data towards small plants does not translate into a bias of upscaled results (see Method and the Supplement, Fig. S8).

The upscaling approach using allometric equations should also tend to overestimate (see the Supplement, “Allometric upscaling” section) the global root biomass due to the curvature of these allometric functions (Enquist and Niklas, 2002; Zens and Webb, 2002). The global forest root biomass ranged between 154–210 Pg when root biomass was upscaled through different allometric equations collected from the literature and fitted to our database (Supplement, Table S7), which is generally larger than from the RF mapping. The global root biomass is likely to be smaller than when applying the allometric equation to the spatial average of shoot biomass (Supplement, Figs. S14–S17). Thus, future in situ characterization of the distribution of tree sizes across the world's forests (see the Supplement, “Allometric upscaling” section) would greatly improve root biomass quantification. Note that how well our global estimate reflects the real root biomass is conditioned upon the accuracy of the in situ root measurement database used to train our RF model. Under-sampling is a common issue in many root studies due to the fractal distribution of root systems in soils and the difficulty of implementing an efficient sampling strategy (Taylor et al., 2013), especially for large trees. We did not quantify the uncertainty in our estimates associated with in situ root measurements due to lack of reliable information.

An accurate spatially explicit global map of root biomass helps to improve our understanding of Earth system dynamics by facilitating fundamental studies on resource allocation, carbon storage, plant water uptake, nutrient acquisition and other aspects of biogeochemical cycles. For example, the close correlation (correlation coefficient of 0.8) between root biomass and rooting depth (Fan et al., 2017) at the global scale and the importance of roots for plant water uptake and transpiration reflect close interactions between vegetation and hydrological cycles. The quest for drivers that affect allocation and consumption of photosynthetic production is a major focus of comparative plant ecology and evolution, as well as the basis of plant life history, ecological dynamics and global changes (McCarthy and Enquist, 2007). Turnover time and allocation are two key aspects that contribute to large uncertainties in current terrestrial biosphere model predictions (Bloom et al., 2016; Friend et al., 2014). Our root biomass map does not provide data on turnover or allocation but provides an outcome on their aggregated effects. Future studies combining the root biomass map with upscaled root turnover data could shed light on the allocation puzzle. The growth of the fast-turnover part of roots, mostly fine roots, and leaves are highly linked. If we assume an annual turnover of leaves and fine roots, a preliminary estimation of average forest fine root biomass (from leaf biomass) reaches 6.7–7.7 Pg (see the Supplement, “Preliminary estimation of fine root biomass”). Despite being a small portion of total plant biomass and highly uncertain, fine roots are temporally variable and functionally critical in ecosystem dynamics. Future studies on global distribution and temporal dynamics of fine roots are valuable. Considering specific biomes, tropical savannas would benefit from better root biomass estimation due to their large land area, and in tropical dry forests, field measurements of root and shoot biomass are needed to refine root biomass quantifications.