European topsoil bulk density and organic carbon stock database (0–20 cm) using machine-learning-based pedotransfer functions

Soil bulk density (BD) serves as a fundamental indicator of soil health and quality, exerting a significant influence on critical factors such as plant growth, nutrient availability, and water retention. Due to its limited availability in soil databases, the application of pedotransfer functions (PTFs) has emerged as a potent tool for predicting BD using other easily measurable soil properties, while the impact of these PTFs' performance on soil organic carbon (SOC) stock calculation has been rarely explored. In this study, we proposed an innovative local modeling approach for predicting BD of fine earth (BD_fine) across Europe using the recently released BD_fine data from the LUCAS Soil (Land Use and Coverage Area Frame Survey Soil) 2018 (0–20 cm) and relevant predictors. Our approach involved a combination of neighbor sample search, forward recursive feature selection (FRFS), and random forest (RF) models (local-RF_FRFS). The results showed that local-RF_FRFS had a good performance in predicting BD_fine (R² of 0.58, root mean square error (RMSE) of 0.19 g cm⁻³, relative error (RE) of 16.27 %), surpassing the earlier-published PTFs (R² of 0.40–0.45, RMSE of 0.22 g cm⁻³, RE of 19.11 %–21.18 %) and global PTFs using RF models with and without FRFS (R² of 0.56–0.57, RMSE of 0.19 g cm⁻³, RE of 16.47 %–16.74 %). Interestingly, we found that the best earlier-published PTF (R² = 0.84, RMSE = 1.39 kg m⁻², RE of 17.57 %) performed close to the local-RF_FRFS (R² = 0.85, RMSE = 1.32 kg m⁻², RE of 15.01 %) in SOC stock calculation using BD_fine predictions. However, the local-RF_FRFS still performed better (ΔR² > 0.2) for soil samples with low SOC stocks (< 3 kg m⁻²). Therefore, we suggest that the local-RF_FRFS is a promising method for BD_fine prediction, while earlier-published PTFs would be more efficient when BD_fine is subsequently utilized for calculating SOC stock. Finally, we produced two topsoil BD_fine and SOC stock datasets (18 945 and 15 389 soil samples) at 0–20 cm for LUCAS Soil 2018 using the best earlier-published PTF and local-RF_FRFS, respectively. This dataset is archived on the Zenodo platform at https://doi.org/10.5281/zenodo.10211884 (S. Chen et al., 2023). The outcomes of this study present a meaningful advancement in enhancing the predictive accuracy of BD_fine, and the resultant BD_fine and SOC stock datasets for topsoil across the Europe enable more precise soil hydrological and biological modeling.

1 Introduction

Soil plays a pivotal role in supporting ecosystems and sustaining life on our planet (Rabot et al., 2018). Its physical properties are crucial for various disciplines such as agriculture, environmental science, and land management. Among these properties, soil bulk density (BD) holds particular significance as it serves as a fundamental indicator of soil health, structure, and water-holding capacity. BD directly influences vital factors like plant growth, nutrient availability, and overall soil quality (Dam et al., 2005; Chen et al., 2018; Schillaci et al., 2021). Additionally, BD plays a crucial role in computing the stock of water, chemical elements (e.g., soil organic carbon, SOC), or compounds by soil surface unit or soil volume unit, making it even more essential in soil studies. Nonetheless, the uncertainty in SOC stock estimates arises due to the variations in methods used to substitute for missing BD data (Benites et al., 2007; Dawson and Smith, 2007; Wiesmeier et al., 2012; Z. Chen et al., 2023). It is important to acknowledge that BD in topsoil exhibits considerable variations across different geographical regions due to factors like diverse soil types, climate conditions, vegetation cover, and land cover patterns (Hollis et al., 2012; Lark et al., 2014; Li et al., 2019). These regional disparities underscore the need for a comprehensive understanding of BD in soil research and its implications for various aspects of ecosystem functioning and management.

Characterizing the spatial distribution of BD across a diverse and extensive continent like Europe presents a complex challenge (Chen et al., 2018; Nasta et al., 2020; Palladino et al., 2022; Panagos et al., 2024). Conventional soil sampling and laboratory analyses are time-consuming, costly, and impractical at a broad scale (Makovníková et al., 2017). In response to this challenge, the development of pedotransfer functions (PTFs) has emerged as a powerful approach (Van Looy et al., 2017). PTFs are mathematical models that estimate soil properties, such as BD, based on readily available and easily measurable soil data (e.g., SOC, clay, silt, and sand). These functions serve as invaluable tools for predicting soil properties at unvisited locations, facilitating regional soil mapping, and enhancing our understanding of soil dynamics across vast areas (Chen et al., 2018; Schillaci et al., 2021; Palladino et al., 2022). Furthermore, the incorporation of globally available predictor variables, such as topography and land cover, showed promise in enhancing the effectiveness and applicability of PTFs for gap-filling of BD data (Ramcharan et al., 2017; Bondi et al., 2018; Patton et al., 2019).

Table 1 Summary of previous studies on using PTFs for BD prediction across scales. R² indicates the determination coefficient.

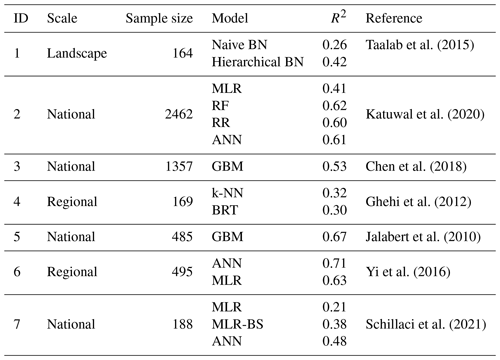
MLR is for multiple linear regression, RF is for random forest, RR is for regression rule, ANN is for artificial neural network, GBM is for generalized boosted model, BRT is for boosted regression tree, BN is for Bayesian network, k-NN is for k nearest neighbor, and MLR-BS is for multiple linear regression (stepwise variable selection).

In the early stage, PTFs predominantly employed regression techniques due to their simplicity (Gupta and Larson, 1979; Rawls and Brakensiek, 1985). However, with advancements in science and technology, a wide range of models have been developed for deriving PTFs, particularly for continuous predicted variables. These methods encompass linear regression, generalized linear models, generalized additive models, regression trees, artificial neural networks, support vector machines, gradient boosted models, and random forests (RFs) (Van Looy et al., 2017; Chen et al., 2018). The utilization of these advanced techniques has substantially improved the accuracy of BD prediction (Table 1).

PTFs have emerged as an alternative approach to address the scarcity of BD data (Van Looy et al., 2017). They have been implemented and tested in diverse regions and countries, providing a practical and cost-effective means for predicting BD using readily available soil properties. However, it is noteworthy that the majority of previous studies utilizing machine learning (ML) and PTFs for BD prediction have been conducted at regional or national scales, with limited research focusing on the intercontinental scale (Taalab et al., 2015; Shiri et al., 2017; Katuwal et al., 2020). Despite the accomplishments of PTFs in BD estimation, a gap emerges when transitioning to global modeling (a fixed model to predict all the unknown samples) endeavors. The reliance on global models, while useful in capturing broad patterns, often faces constraints in delivering accurate predictions at finer scales (Gupta et al., 2018). These global models may fail to account for the nuanced spatial and environmental variations that play a pivotal role in determining BD across different landscapes. While numerous studies have harnessed ML-based PTFs (ML-PTFs) to improve the model performance of BD at national and regional levels, the expansion of these methodologies to encompass continental contexts remains relatively limited (Nasta et al., 2020; Schillaci et al., 2021; Palladino et al., 2022). This gap underscores the need for a modeling approach that bridges the gap between broad-scale global modeling and the context-specific requirements of diverse regions and ecosystems (Wang et al., 2024). This is where the concept of local modeling steps in. The local model adopts a dynamic modeling strategy: it firstly selects a part of similar samples close to each unknown sample in the predictor space, and then it fits a predictive model using the selected similar samples (not the entirety of the data). Since the selected similar samples vary for each unknown sample, the corresponding local model is different from others. A local modeling strategy enables the consideration of environmental relevance by clustering data under similar environmental conditions (i.e., in the present case, similar predictors feature space, including soil properties, elevation, land cover, and climate conditions), which aids in constructing specialized PTFs that capture soil–environment relationships (Nocita et al., 2014; Chen et al., 2018). Thus, there is a compelling need for further investigations of and developments in local modeling techniques to improve BD predictions. Furthermore, despite the wide use of PTFs in predicting BD in SOC stock calculations from continental to global scales, how the performances (e.g., R², root mean square error, relative error) of PTF-based BD prediction impact the quality of SOC stock remains poorly explored (Cotrufo et al., 2019; Augusto and Boča, 2022; Wang et al., 2022; De Rosa et al., 2023).

To address the aforementioned issues, we investigated an RF model in combination with variable selection and a local modeling strategy to evaluate the potential of different PTFs in BD prediction, as well as in SOC stock calculation. The main objectives of this study are as follows:

1. to compare the performances of earlier-published PTFs and ML-PTFs for BD prediction

2. to evaluate the potential of local modeling strategies for BD prediction

3. to investigate the impact of PTF-based BD prediction on the accuracy of SOC stock calculation.

Figure 1 Spatial distribution of 5163 topsoil samples with estimated BD_fine from LUCAS Soil 2018. The colors represent six BD_fine levels, and the histogram represents the relevant percentages for these BD_fine levels.

2 Materials and methods

2.1 Soil data

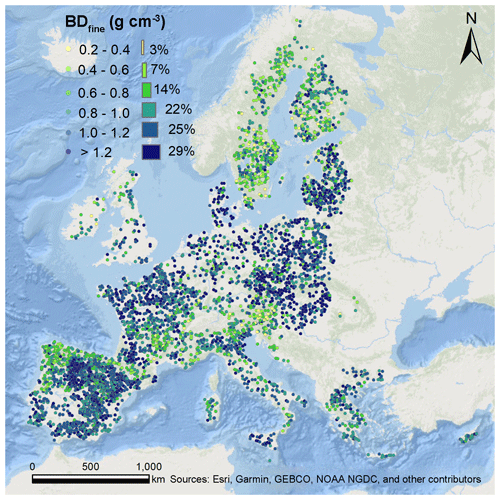
The soil data were compiled from the Land Use and Coverage Area Frame Survey Soil (LUCAS Soil) campaigns conducted in 2009, 2015, and 2018 (Fernández-Ugalde et al., 2022; Panagos et al., 2022). The survey encompassed a stratified random sampling approach, which identified approximately 20 000 topsoil sampling locations across the European Union (EU) and the United Kingdom (UK) for each campaign. At each sampling site (circle of 4 m diameter plot), five topsoil samples (0–20 cm) were collected after the removal of the litter layer, and the land cover (LC) was recorded. These samples were then combined into a bulked composite topsoil sample for analysis. Subsequently, all topsoil samples underwent air-drying and sieving to less than 2 mm. Standard laboratory analysis was conducted in an accredited laboratory (Kecskemét, Hungary), including particle size fractions (clay content, silt content, sand content, %), coarse fragments (mass fraction, %/100), BD (whole mass, g cm⁻³), pH (in water), SOC content (g kg⁻¹), carbonates (CaCO₃, g kg⁻¹), total nitrogen (N, g kg⁻¹), extractable potassium (K, mg kg⁻¹), and cation exchange capacity (CEC, $\mathrm{cmol}(+){\mathrm{kg}}^{-\mathrm{1}}$). For more comprehensive information about LUCAS Soil 2009/2015/2018, we refer the reader to Orgiazzi et al. (2022). In the LUCAS Soil 2018 survey, topsoil sampling was conducted across all EU Member States and the UK, employing the identical set of 25 947 locations that were targeted during the 2015 survey (Fernández-Ugalde et al., 2022). However, due to the absence of particle size fractions in LUCAS Soil 2018, we resorted to using the data from LUCAS Soil 2009/2015 according to the unique identifier soil ID (Panagos et al., 2022). To ensure the reliability of the data, we excluded samples with soil particle fractions recorded as 0. Finally, 5163 topsoil samples were retained for further analysis (Fig. 1). In the following parts of the article, we define BD_sample as the whole soil mass : volume ratio and BD_fine as the fine-earth mass : volume ratio.

Since BD_sample was measured for the whole mass and CF was measured as a mass fraction (CF_massfraction) in part of the topsoil samples of the LUCAS Soil 2015/2018, they cannot be used directly to accurately calculate SOC stock. Note that, if the mass of the fine fraction has been measured and recorded (as the total volume of the sample is known), the SOC stock can be calculated directly (Poeplau et al., 2017). However, in numerous locations, neither the mass of the fine fraction nor BD_sample was measured. This is why we needed to estimate and use BD_fine and CF_{volumefraction} in order to calculate SOC stocks where BD_sample was missing (Poeplau et al., 2017). To this aim, we used a recently released dataset for BD_fine and CF_{volumefraction} by Pacini et al. (2023) based on BD_sample and CF_massfraction from LUCAS Soil 2018.

2.2 Predictor variables related to relief, climate, and land cover

The elevation (ELE) was derived from the Shuttle Radar Topography Mission (SRTM) 1 km digital elevation model (Farr et al., 2007). Climatic data, including mean annual precipitation (MAP) and mean annual temperature (MAT), were acquired from the WorldClim version 2 at 1 km resolution (Fick and Hijmans, 2017). The Global-PET dataset at 1 km resolution was used to extract potential evapotranspiration (PET) and aridity index (AI) (Zomer et al., 2022). The land cover (LC) was directly derived from the records of LUCAS Soil 2018 during the soil sampling campaign.

Table 2 Summary of four earlier-published PTFs defined in the literature.

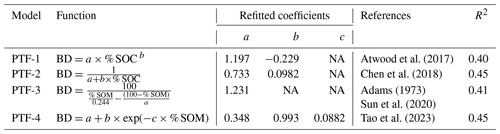
BD is for bulk density; depending on the authors cited in references, BD has been considered to be the BD of the fine fraction (BD_fine) or the BD of the whole sample (BD_sample) (both expressed in g cm⁻³); here, the refitted coefficients correspond to BD_fine. SOM is for soil organic matter content (% in soil mass). SOC is for soil organic carbon content (% in soil mass). NA: not available.

2.3 Earlier-published PTFs

We evaluated four earlier-published PTFs that have been widely used to estimate BD_sample or BD_fine in previous studies at both local and broad scales (Adams, 1973; Atwood et al., 2017; Chen et al., 2018; Sun et al., 2020; Tao et al., 2023). For PTF-3 and PTF-4, soil organic matter (SOM) content was determined by the conversion factor of 1.724 using SOC content. In the present study, we used these PTFs to estimate BD_fine. The parameters in these PTFs were refitted by the Levenberg–Marquardt nonlinear least-square method available in the minpack.lm R package based on our data (Bates and Watts, 1988; Zhu et al., 1997; Elzhov et al., 2015). These refitted parameters of PTFs are present in Table 2.

Table 3 The variables used in RF_Full and RF_FRFS. For RF_FRFS; the order of the variables is by descending importance. RF_Full uses all potential predictors, even if they may be redundant of multi-collinear (typical case of the use of clay, silt, and sand contents together). RF_FRFS applies FRFS, thus eliminating both multi-collinearity and irrelevant predictor variables (e.g., one particle size fraction (sand content) is left out). The abbreviations are detailed as follows: SOC is for soil organic carbon content, CEC is for cation exchange capacity, AI is for aridity index, PET is for potential evapotranspiration, MAP is for mean annual precipitation, MAT is for mean annual temperature, ELE is for elevation, and LC is for land cover. Clay, silt, sand, and CaCO₃ are expressed in %; pH is pH in a 1:2.5 soil:water mixture.

2.4 Global ML-PTFs

To compare with earlier-published PTFs, we used a random forest (RF) model to construct global ML-PTFs for predicting BD_fine. RF is an ensemble learning method that aggregates predictions from multiple decision trees to obtain the final estimates of the target variable. In growing a decision tree, a random subsample of data is selected from the verification dataset, and a set of random predictor variables is used for splitting the subsampled data. Two parameters, ntree and mtry, were optimized by 10-fold cross-validation. Here, 15 predictor variables, such as sand content, silt content, clay content, SOC content, and ELE (Table 3), were used to build the global RF model.

Furthermore, we adopted a recently proposed variable selection method, namely forward recursive feature selection (FRFS), to reduce the number of predictor variables while not losing model performance (Xiao et al., 2022a; Zhang et al., 2023). FRFS employs a forward selection strategy, involving the following sequential steps: (1) initially, an RF model is fitted using all the n predictors, and their variable importance is calculated; (2) the most important predictor (only one) is selected to create an initial model, and its performance is assessed using 10-fold cross-validation with a single predictor in the pool; (3) subsequently, a series of models are constructed using two predictors, where the first predictor is chosen from the pool, and the second predictor is selected from the remaining predictors. The model performances are evaluated, and the model with the best performance is recorded; (4) the pool of predictors is then updated based on the predictors from the best-performing model in the previous step; (5) the process is iteratively repeated, progressively increasing the number of predictors from 3 to n. Ultimately, the predictors used in the model with the best performance are selected to form the final predictive model, as detailed in the work of Xiao et al. (2022a). The R script for implementing FRFS is accessible at https://doi.org/10.5281/zenodo.7141020 (Xiao et al., 2022b). In this study, FRFS was applied to select the most relevant predictors constructing the predictive models (Table 3).

For clarity, in global modeling, we refer to the RF model using the full variables as global-RF_FULL and the combination of the RF model with FRFS as global-RF_FRFS.

2.5 Local ML-PTFs

The development of local ML-PTFs consists of four steps: (1) use the Mahalanobis distance to calculate the distances of predictor variables between each sample to be predicted and all the samples in the database; (2) select k nearest-neighbor samples to fit an RF model for each unknown sample; (3) predict the BD_fine for each unknown sample using relevant RF models. Since the number of nearest-neighbor samples (k) is an important parameter in the local model, we evaluated its effect on the model performance by testing k from 20 to 700 (20, 40, 60, 80, 100, 150, 200, 250, 300, 350, 400, 450, 500, 550, 600, 650, 700).

For clarity, we refer to the local modeling using the full variables as local-RF_FULL, and we refer to the combined use of the RF model and variables selected by global-RF_FRFS as local-RF_FRFS.

2.6 Model evaluation

Due to the large sample size, a single random split is stable compared to k-fold cross-validation or a repeated random split (Chen et al., 2021). Therefore, we used a random split (80 % for calibration and 20 % for validation) to assess the model performance of earlier-published PTFs and ML-PTFs. It is important to note that the same validation set was used to evaluate earlier-published PTFs and ML-PTFs. The root mean square error (RMSE), determination coefficient (R²), and relative error (RE) were used as performance indicators in the validation set (Chen et al., 2022). These indices are defined following Eq. (1), (2), and (3):

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }\mathrm{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{n}}{\sum }_{i=\mathrm{1}}^n(O_i-P_i{)}^{\mathrm{2}}},\text{(2)}& {\displaystyle }& {\displaystyle }{R}^{\mathrm{2}}=\mathrm{1}-{\displaystyle \frac{{\sum }_i^n(O_i-P_i{)}^{\mathrm{2}}}{{\sum }_i^n{\left(O_i-\stackrel{\mathrm{‾}}{O}\right)}^{\mathrm{2}}}},\text{(3)}& {\displaystyle }& {\displaystyle }\mathrm{RE}={\displaystyle \frac{\mathrm{1}}{n}}\sum _{i=\mathrm{1}}^n{\displaystyle \frac{\left|O_i-P_i\right|}{O_i}}\times \mathrm{100}\mathit{\%},\end{array}$$

where n represents the number of observations, O_i and P_i are the observed and predicted BD_fine for observation i, and $\stackrel{\mathrm{‾}}{o}$ is the mean of the observed BD_fine. A good model has an RMSE and RE close to 0 and also higher R² close to 1.

2.7 The build-up of extended BD_fine and SOC stock datasets for topsoil in Europe

Since only part of LUCAS 2015/2018 had soil particle fractions and CaCO₃, we used the unique sample ID to link the missing soil particle fractions and CaCO₃ using LUCAS Soil 2009 for the same sampling sites. This operation is reasonable since soil particle fractions and CaCO₃ will not have experienced a notable change within a decade. The SOC stock (kg m⁻²) at a depth of 0–20 cm for LUCAS Soil 2018 was calculated by the SOC content (g kg⁻¹), BD_fine (g cm⁻³), CF_{volumefraction} ($\mathit{\%}/\mathrm{100}$), and depth (20 cm) as in Eq. (4) (Poeplau et al., 2017).

$$\begin{array}{}\text{(4)}& \begin{array}{rl}\text{SOC\hspace{0.17em} stock}=& \mathrm{SOC}\times {\mathrm{BD}}_{\mathrm{fine}}\times \mathrm{Depth}\\ & \times (\mathrm{1}-{\mathrm{CF}}_{\mathrm{volumefraction}})/\mathrm{100}\end{array}\end{array}$$

Figure 2 Histogram of BD_fine (a) and USDA soil texture triangle (b). The point colors shown in the texture triangle correspond to the colors present in the left histogram. The percentage of each bin is indicated over the bin in the histogram.

3 Results

3.1 Statistics of BD_fine and its correlation with predictor variables

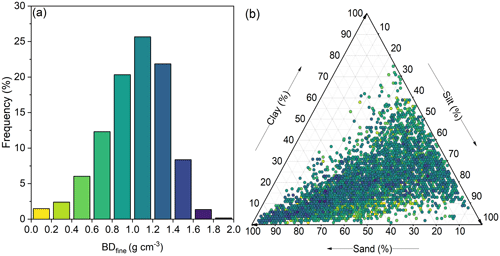
Figure 2 illustrates the histogram of BD_fine values and their distribution in a ternary soil texture triangle. The dataset consists of 5163 topsoil samples, with BD_fine ranging from 0.20 to 1.89 g cm⁻³. The topsoil sample with the lowest BD_fine (0.20 g cm⁻³) was collected from a pine-dominated mixed woodland with an SOC content greater than 137 g kg⁻¹. In contrast, the topsoil sample with the highest BD_fine (1.89 g cm⁻³) was sampled from a sandy soil (sand and clay of 65 % and 11 %, SOC content of 31.9 g kg⁻¹) in cropland (common wheat). Approximately half of the topsoil samples exhibited BD_fine between 0.8 and 1.4 g cm⁻³, while less than 10 % of the topsoil samples had BD_fine exceeding 1.4 g cm⁻³. As shown in the soil texture triangle, the selected topsoil samples covered a wide range of soil texture classes.

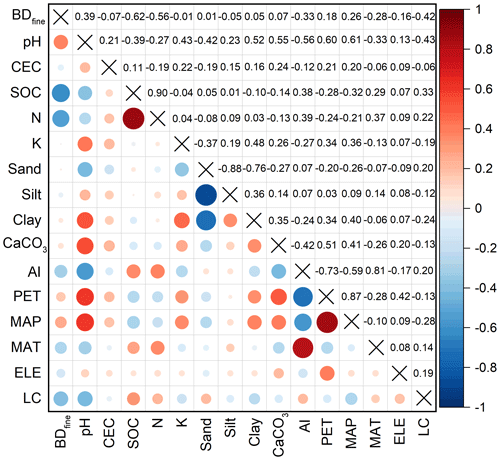
Figure 3 Correlation plot of BD_fine and predictors. The sizes of the circles represent the magnitudes of the correlation, and light and dark colors represent negative and positive correlations, respectively. The abbreviations are detailed as follows: BD_fine is for bulk density of fine earth, CEC is for cation exchange capacity, SOC is for soil organic carbon content, AI is for aridity index, PET is for potential evapotranspiration, MAP is for mean annual precipitation, MAT is for mean annual temperature, ELE is for elevation, and LC is for land cover.

Figure 3 depicts the correlation matrix between BD_fine and 15 predictor variables. BD_fine exhibited positive correlations with pH and MAT, with correlation coefficients (r) greater than 0.25. On the other hand, BD_fine showed notably high negative correlations with most of the other predictors. The most influential negative predictor was SOC content (r = −0.62), followed by N (r = −0.56) and CaCO₃ (r = −0.33). Note that BD_fine under various LC classes exhibited significant differences in terms of mean BD_fine of 1.16, 1.00, 0.78, and 1.02 g cm⁻³ for cropland, grassland, woodland, and others, respectively.

3.2 Selection of predictor variables

Table 3 presents the predictor variables utilized in the RF model for predicting BD_fine. In the global-RF_FULL model, 15 predictor variables were included, namely clay content, silt content, sand content, pH, SOC content, CaCO₃, N, K, CEC, AI, PET, ELE, MAP, MAT, and LC. On the other hand, the global-RF_FRFS identified a subset of eight predictor variables by means of FRFS that were deemed to be most important for BD_fine prediction. These selected predictor variables, ranked in descending order of importance, were SOC content, N, pH, PET, MAP, LC, AI, and MAT.

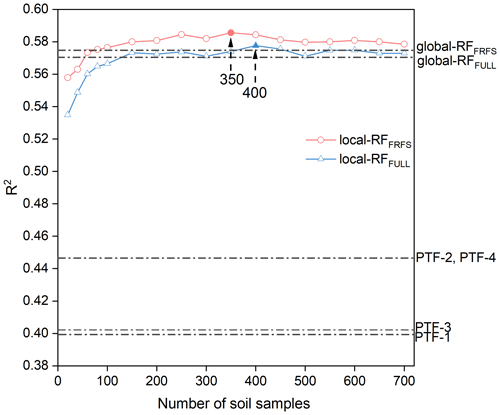
Figure 4 Model performance indicator (R²) of earlier-published PTFs and ML-PTFs in BD_fine prediction. The performances of local RF models (local-RF_FULL and local-RF_FRFS) change with the number of soil samples used for local modeling.

Figure 5 Scatter plots of BD_fine predictions using earlier-published PTFs and ML-PTFs along with model performance indicators (RMSE, R², and RE). The lighter color indicates a higher sample density. Please note that the best models are selected for local-RF_FULL and local-RF_FRFS.

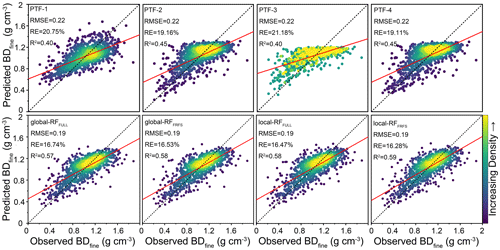
3.3 Comparison of ML-PTFs and earlier-published PTFs in BD_fine prediction

In this study, we compared ML-PTFs with four earlier-published PTFs in BD_fine prediction (Figs. 4 and 5). The earlier-published PTFs had model performances with an RMSE of 0.22 g cm⁻³, R² of 0.40–0.45, and RE of 19.11 %–20.75 %. The global-RF models had higher model performances, with an RMSE of 0.19 g cm⁻³, R² between 0.57 and 0.58, and RE of 16.53 %–16.74 % for global-RF_FULL and global-RF_FRFS, respectively, though the latter performed slightly better (see R² values in Fig. 4). As for local models, it was clear that the model performance showed an increasing trend when the number of neighbor samples increased, and some fluctuations were observed after the model performance reached a plateau. The number of neighbor samples was optimized at 350 and 400 for local-RF_FRFS and local-RF_FULL, respectively. Compared to global modeling, the best local-RF_FRFS and local-RF_FULL performed slightly better with R² of 0.59–0.57 and RE of 16.28 %–16.47 %.

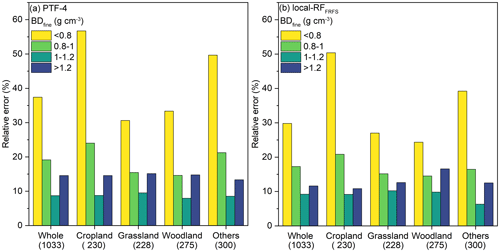
Figure 6 The variations in RE related to BD_fine ranges of values (< 0.8, 0.8–1, 1–1.2, and > 1.2 g cm⁻³) and land covers using PTF-4 (a) and local-RF_FRFS (b). The number under the land cover is the corresponding topsoil sample size.

The summary of RE variations under different BD_fine levels and land covers using best earlier-published PTF (PTF-4) and ML-PTF (local-RF_FRFS) is shown in Fig. 6. The results indicated that local-RF_FRFS (RE of 29 %) performed much better than PTF-4 (RE of 37 %) for the topsoil with low BD_fine (< 0.8 g cm⁻³). The improvement in RE for other BD levels was rather limited (ΔRE of 1 %–3 %). The highest RE (30 %–57 % for PTF-4, 25 %–50 % for local-RF_FRFS) was found for topsoil with low BD_fine for the whole validation set and each land cover. Across land covers, the RE generally decreased greatly (15 %–24 % for PTF-4, 14 %–20 % for local-RF_FRFS) for topsoil with low–median BD_fine (0.8–1 g cm⁻³) and then decreased to its lowest (7 %–9 % for both PTF-4 and local-RF_FRFS) for topsoil with median–high BD_fine (1–1.2 g cm⁻³). A slight increase in RE (14 %–16 % for PTF-4, 11 %–17 % for local-RF_FRFS) was observed for topsoil with high BD_fine (> 1.2 g cm⁻³) for all the land covers. Among different land covers, the cropland had the greatest RE for topsoil with low and low–median BD_fine, followed by others, woodland, and grassland. For topsoil with median–high and high BD_fine, a similar RE was found for all the land covers. Overall, the RE for both PTF-4 and local-RF_FRFS showed the worst performances for low BD_fine, but the results were always better for local-RF_FRFS, except for woodlands with BD_fine > 1, where the RE was slightly better for PTF-4.

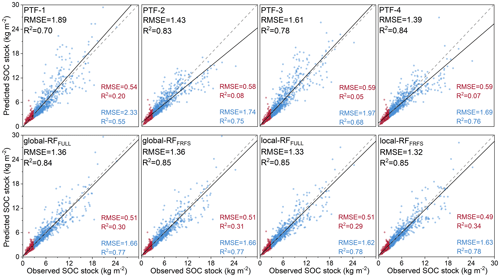
Figure 7 Scatter plots of SOC stock predictions by earlier-published PTFs and ML-PTFs along with model performance indicators (RMSE, R², and RE). The red points represent topsoil samples with SOC stock < 3 kg m⁻², while the blue points represent topsoil samples with SOC stock ≥ 3 kg m⁻². Note that observed SOC stock is computed using SOC content, CF_{volumefraction}, and BD_fine observations, and while predicted SOC stock is computed using SOC content observations, BD_fine predictions and CF_{volumefraction} are transformed from CF_massfraction using BD_fine predictions, as suggested by Pacini et al. (2023).

3.4 Comparison of ML-PTFs and earlier-published PTFs in SOC stock calculation

We investigated how using BD_fine estimated by PTFs impacted the accuracy of SOC stock calculation (Fig. 7). We found that SOC stock calculation using BD_fine predictions from four earlier-published PTFs resulted in a good performance, with an RMSE of 1.39–1.89 kg m⁻², R² of 0.70–0.84, and RE of 17.57 %–19.46 %. Meanwhile, the performance indicators of SOC stock calculation using BD_fine prediction (RMSE of 1.32–1.36 kg m⁻², R² of 0.84–0.85, RE of 15.01 %–15.41 %) always exhibited slightly better performances than the earlier-published PTFs. However, the performances of the best earlier-published PTF (PTF-4) were rather similar to those of the local-RF_FRFS. Overall, the performances of the local-RF_FRFS were the best.

Figure 8 Spatial distributions of 15 389 topsoil samples with BD_fine (a) and SOC stock (b) from LUCAS 2018 Soil using local-RF_FRFS and 18 945 topsoil samples with BD_fine (c) and SOC stock (d) from LUCAS 2018 Soil using PTF-4.

3.5 Summary of the extended European topsoil BD_fine and SOC stock database

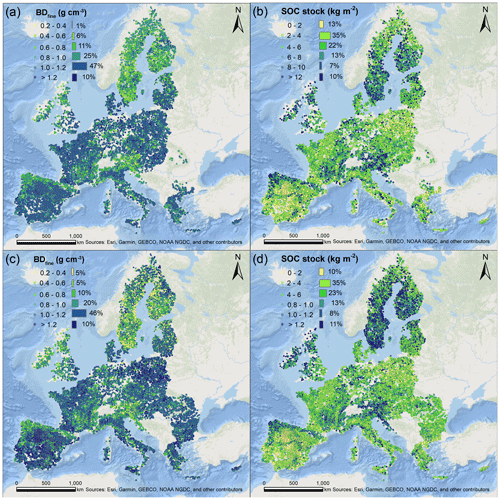
To enlarge the topsoil BD_fine and SOC stock database (0–20 cm) for Europe, we refitted the best ML-PTF (local-RF_FRFS) and the best earlier-published PTF (PTF-4) using all 5163 topsoil samples to predict topsoil samples without BD_fine, and then we calculated SOC stock, which resulted in 15 389 and 18 945 topsoil sample predictions for the extended database, respectively (fewer topsoil samples had all the required variables for the use of local-RF_FRFS). As shown in Fig. 8, these extended topsoil BD_fine and SOC stock databases are more regularly distributed across the EU and UK compared to the points in Fig. 1. In the EU and UK, BD_fine in topsoil was primarily distributed within 1.0–1.2 g cm⁻³ (46 %–47 %), while the SOC stock in topsoil was mainly comprised between 2 and 4 kg m⁻².

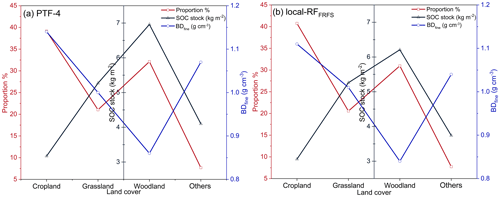
Figure 9 Variations in topsoil BD_fine and SOC stock under different land covers using PTF-4 (a) and local-RF_FRFS (b).

As shown in Fig. 9, in the database created by local-RF_FRFS (15 389 topsoil samples), the topsoil samples under cropland had the highest median BD_fine of 1.11 g cm⁻³, while woodland exhibited the lowest median BD_fine at 0.84 g cm⁻³. Conversely, woodland had the highest median SOC stock at 6.21 kg m⁻², while cropland showed the lowest median SOC stock at 3.06 kg m⁻². As for the database built on PTF-4 (18 945 topsoil samples), cropland also had the highest median BD_fine at 1.14 g cm⁻³, while woodland exhibited the lowest median BD_fine at 0.86 g cm⁻³. In contrast, the SOC stock under woodland presented the highest median SOC stock at 6.96 kg m⁻², while cropland had the lowest median SOC stock at 3.17 kg m⁻².

4 Discussion

4.1 The superiority of ML-PTFs in BD_fine prediction

In this study, using the LUCAS Soil and 15 predictor variables, we compared the model performance of four earlier-published PTFs and four ML-PTFs for BD_fine in topsoil (0–20 cm). Four earlier-published PTFs showed a moderate model performance with R² of 0.40–0.45, which is close to a recently developed Hollis-type PTF (R² of 0.41, Hollis et al., 2012) that was refitted with LUCAS Soil 2018 data (De Rosa et al., 2023). Our results underscored the efficacy of ML-PTFs in successfully predicting BD_fine at a continental scale, yielding a substantial R² ranging from 0.57 to 0.59. This indicates that, when adding more relevant predictor variables (e.g., N, pH, PET, MAP) to the topsoil database, ML-PTFs is a better choice for improving BD_fine prediction than earlier-published PTFs based on algebraic equations. Otherwise, earlier-published PTFs are still the best choice to impute the missing data due to their simplicity (Van Looy et al., 2017).

In addition to global PTFs that use all the soil samples, we introduced the local modeling strategy in PTFs, which searched similar samples first and then built the relevant PTF for each unknown sample dynamically. Generally, the model performance of local PTFs (local-RF_FULL and local-RF_FRFS) for BD_fine prediction continuously improved with the increasing number of neighbor samples, and then it reached a plateau when the number of neighbor samples reached approximately 350 to 400 (Fig. 4). Compared to the global PTFs (4500 soil samples), the sizes of local PTFs were much smaller (350–400 soil samples) with slightly better model performance. Therefore, the comparison between global PTF and local PTF performances shows that local PTFs can improve the efficiency of imputing missing data using a large soil database (Padarian et al., 2019; Sanderman et al., 2020).

In comparison to the earlier-published PTFs that were refitted using our data, the local-FR_FRFS model substantially improved model performance in BD_fine prediction (ΔR² of 0.14–0.19). Our results suggest that ML-PTFs performed much better than earlier-published PTFs for BD_fine prediction. This resulted from the fact that most of the ML models are able to handle nonlinear and complex relationships between the predictor variables and the response variable, thereby improving predictions compared to those of earlier-published PTFs (Katuwal et al., 2020; Palladino et al., 2022). Meanwhile, the earlier-published PTFs typically rely solely on SOC or SOM content for BD_fine prediction. This approach maintains model simplicity but overlooks readily available predictor variables such as particle size fractions, MAT, and MAP, which are also pertinent to BD_fine prediction (Abdelbaki, 2018). Despite the high diversity in landscapes and climates at a continental scale, the proposed local-FR_FRFS model demonstrated similar or even superior performance compared to the ML-PTFs conducted at regional and national scales (Table 1).

Looking into the RE for topsoil under different BD_fine levels (Fig. 6), it is clear that the best-fitted PTFs (PTF-4 and local-RF_FRFS) had the highest REs for topsoil with low BD_fine (< 0.8 g cm⁻³) despite the fact that local-RF_FRFS performed better. This partly results from the low BD_fine required to calculate the RE because the BD_fine value is used as the reference 100 % value in RE calculation. This is also likely due to the general trend of broad-scale predictions smoothing the variability and overestimating the low values and underestimating the high values, whatever the predicted variable is (e.g., Tifafi et al., 2018; Lemercier et al. 2022; Richer-de-Forges et al., 2023). Most importantly, many low BD_fine observations are probably linked to large voids, resulting in a large porosity, especially under disturbed topsoil. This explains why cropland topsoil exhibited such a large RE, likely due to the effect of soil tillage which cannot be predicted by our predictor variables. This can also explain the decreasing trend in RE with the increase in BD_fine up to 1.2 g cm⁻³, whereas, for the topsoil with high BD (> 1.2 g cm⁻³), both local-RF_FRFS and PTF-4 showed a slight increase in RE. Overall, the RE values might appear to be a bit deceiving if we compare them to the accuracy that one may wish for in monitoring changes in BD_fine – for example, as an indicator of compaction. We must state that this is clearly out of the scope of this study, which is intended to provide a wide database that can be used for broad-scale modeling.

4.2 Performance of FRFS and variable importance in BD_fine prediction by ML-PTFs

We reduced the number of predictor variables in the RF model from 15 to 8 using the FRFS algorithm, and the model performance of global-RF_FRFS for BD_fine using FRFS-selected variables was higher than that of global-RF_FULL using full variables (Table 3). Though the local-RF_FRFS (R² of 0.59) only had marginal superiority over the local-RF_FULL model (R² of 0.58), it facilitated the reduction of variables, consequently enhancing prediction efficiency (Figs. 4 and 5). This outcome validates the capacity of FRFS to simplify the model complexity while concurrently enhancing its predictive accuracy (Xiao et al., 2022a; Liu et al., 2023; Zhang et al., 2023; Hu et al., 2024). Being a useful tool for gap-filling the missing data, an ideal PTF requires both high parsimony and good fit. If the developed PTF needs too many predictors variables, its practical applicability would be limited as much fewer soil samples have all the required predictor variables.

4.3 The build-up of extended BD_fine and SOC stock datasets in Europe

We used the BD_fine predictions from eight PTFs together with CF_{volumefraction} to calculate the SOC stock. The results showed that the model performances of SOC stock (R² of 0.70–0.85) were much higher than those of BD_fine (R² of 0.40–0.59) (Figs. 5 and 7). This can be explained by the interdependence between BD_fine and SOC content. For instance, a soil sample with a high SOC content commonly has a large pore space due to the large amount of organic matter, leading to a low BD_fine (Perie and Ouimet, 2008; Chen et al., 2018). As shown in Fig. 7, high SOC content and BD_fine were always underestimated, while the low SOC content and BD_fine were overestimated. By multiplying these two negatively correlated variables, the predicted SOC stock could be closer to the observed SOC stock as the overestimation (underestimation) of BD_fine can counterbalance the underestimation (overestimation) of SOC content, resulting in better model performance than BD_fine. It is interesting to note that the model performances of the best earlier-published PTFs (PTF-4, R² of 0.84) and ML-PTFs (local-RF_FRFS, R² of 0.85) were quite close in terms of SOC stock prediction. This indicated that the improvement of BD_fine prediction by ML-PTFs did not impact the accuracy of SOC stock prediction. Looking into the scatter plots shown in Fig. 5, we can observe that the ML-PTFs performed much better than earlier-published PTFs for topsoil samples with high BD_fine (and low SOC content), while a limited difference was found for soil samples with low BD_fine (and high SOC content). Compared to earlier-published PTFs, ML-PTFs tended to predict SOC stock better for topsoil samples with low SOC stock (< 3 kg m⁻²), while similar model performances can be found in topsoil samples with high SOC stocks (≥ 3 kg m⁻²), which is evident in Fig. 5. As a result, the best earlier-published PTF (PTF-4) performed quite similarly to the best ML-PTF (local-RF_FRFS) when considering the topsoil samples with a wide range in terms of SOC stock. This last result suggests that earlier-published PTFs could be useful default tools in estimating BD_fine which is subsequently used for SOC stock calculation. One of the advantages of these earlier-published PTFs is their simplicity; another obvious advantage is that they require fewer training soil samples than ML-PTFs to be fitted and validated. Otherwise, if enough data are available, ML-PTFs are suggested for more accurate BD_fine prediction, especially for regions with low SOC stocks, such as dry land regions in Spain and Italy (Maestre et al., 2021; De Rosa et al., 2023; Wang et al., 2023).

4.4 Limitations and perspectives

It is essential to acknowledge that our developed PTFs for BD_fine prediction were constructed based on LUCAS Soil data (0–20 cm), confining their applicability to topsoil within the EU and UK (Orgiazzi et al., 2022, Panagos et al., 2022). However, the potential of their extrapolation capability to other regions or to deep soil (> 20 cm) necessitates further evaluation. As more soil data become available from diverse regions, as well as for deep soil (Lal, 2018; Tautges et al., 2019; Batjes et al., 2020; Yost and Hartemink, 2020; Palmtag et al., 2022; Armas et al., 2023), the proposed methodology can be further used to update the PTFs, thereby broadening their area of applicability (Chen et al., 2018; Meyer and Pebesma, 2021). In addition, when a depth-specific soil BD_fine database is available, it will be important to develop depth-explicit ML-PTFs to account for the effects of climate and topography on BD_fine at depths.

We acknowledge that our use of PTF-3 and PTF-4 is based on measured SOC contents and on a fixed Van Bemmelen factor (SOM = 1.724 × SOC, Sprengel, 1826; Van Bemmelen, 1890). One good reason to use this factor is that it enables a comparison with most of the studies predicting BD_fine using SOC and other soil properties. One pitfall is that we know that the conversion factor from SOC to SOM is not constant (Pribyl, 2010). However, this conversion factor was only used for PTF-3 and PTF-4. Considering the equations used, changing this conversion factor for PTF-4 has no consequence on the predicted BD_fine or on the model performance of the PTF for BD_fine prediction. Changing it for PTF-3 will lead to lower performance. We have no clear indication that we ought to try to adapt the Van Bemmelen factor to the pedological context (or to the effect of SOC on BD_fine) when we use fixed regressions such as PTF-3 and PTF-4. One advantage of ML-PTFs, and especially of local ML-PTFs, is that they can take into account interactions between soil properties. Therefore, the importance of SOC likely varies depending other local controlling factors such as clay content, climate, or even the nature of the organic compounds, which could explain the strong effect of N. In other words, ML-PTFs were able to partially compensate for the effect of using a fixed conversion factor between SOC and SOM. It should be noted that the BD_fine and CF_{volumefraction} used in this study have been transformed from BD_sample and CF_massfraction by Pacini et al. (2023), which certainly introduced some uncertainty. However, for topsoil samples with CF close to 0, the uncertainty from data transformation is rather low. Since many cropland soils have CF close to 0, and because they are the most sensitive to threats, the proposed PTFs for BD_fine prediction would be helpful.

Another possible source of error is linked to re-allocating some measured values from one LUCAS Soil sampling campaign to another one. Indeed, BD (whether BD_fine or BD_sample) is highly variable in space and time, and coarse fragments and SOC are highly variable in space. The location of sampling may change slightly between LUCAS Soil campaigns for various reasons, and the instructions recommend a distance of < 100 m (Fernández-Ugalde et al., 2017). This latter case has no reason to induce a systematic bias. However, it increases the uncertainty (Munera-Echeverri et al., 2022). Finally, soils containing large amounts of large rocks are clearly excluded from the LUCAS Soil protocol; therefore, one should keep this in mind so as to not extrapolate BD_fine and SOC stock predictions to rocky soils.

If one wants to use PTF-based BD_fine prediction to detect SOC stock changes, the impact of the performance of PTFs on the accuracy of SOC stock calculation remains unclear since the equivalent soil mass approach also requires BD_fine as input (Schrumpf et al., 2011; Wendt and Hauser, 2013). Therefore, this issue could be investigated in future studies. However, the most straightforward and unbiased way to measure SOC stocks by sampling remains the direct determination of the ratio of the fine-earth mass:sample volume by sieving and weighting the fine soil from a sample of known volume.

Most of the predictor variables that we used for ML-PTFs are prone to changes at different timescales. This is the case for all predictor variables derived from climate. Some soil predictor variables (e.g., SOC, pH) can change more or less rapidly under the effect of practices, LC changes, and global changes. Finally, LC can change at any given time, though some effect of past LC may remain for a given time. Though strong perturbations may have an immediate effect on BD_fine, the timescales at which most of these predictor variables influence or are just correlated to BD_fine remain unclear. This opens the door to further questioning about the processes that govern the importance of these predictor variables to BD_fine. Indeed, ML tools can be used as simple predictors at a given time or as tools to raise attention with regard to the possible effects of some controlling factors and their changes and the processes involved in these effects.

5 Data availability

All the soil data used in this article are available at the following data sources: (1) Land Use and Coverage Area Frame Survey Soil (LUCAS Soil) 2009 via https://esdac.jrc.ec.europa.eu/content/lucas-2009-topsoil-data (European Commission, 2013; Panagos et al., 2022), (2) LUCAS Soil 2015 via https://esdac.jrc.ec.europa.eu/content/lucas2015-topsoil-data (European Commission, 2020; Fernández-Ugalde et al., 2022), and (3) LUCAS Soil 2018 via https://esdac.jrc.ec.europa.eu/content/lucas-2018-topsoil-data (European Commission, 2022; Panagos et al., 2022); (4) the European topsoil BD_fine and SOC stock dataset (0–20 cm) in this paper is available at https://doi.org/10.5281/zenodo.10211884 (S. Chen et al., 2023).

6 Conclusions

Using the largest extendable soil dataset for Europe, we have developed ML-PTFs for predicting BD_fine at 0–20 cm across the EU and UK. In comparison to four earlier-published PTFs, the best ML-PTF, namely local-RF_FRFS, exhibited superior performance for BD_fine prediction with a percentage increase in R² at 31.1 %–47.5 % and a percentage decrease in RMSE and RE at 13.6 % and 14.8 %–23.1 %, respectively. When the predicted BD_fine was subsequently used for SOC stock calculation, we found that the best earlier-published PTF preformed quite similarly to the best ML-PTF, indicating the fact that earlier-published PTFs would be useful for BD_fine prediction when targeting SOC stock calculation. However, for regions with low SOC stock (< 3 kg m⁻²), ML-PTFs are still recommended due to their high accuracy in SOC stock calculation. Finally, we established two comprehensive pan-European topsoil BD_fine and SOC stock databases (0–20 cm) including 15 389 and 18 945 soil samples from LUCAS Soil 2018 using the best ML-PTF (local-RF_FRFS) and an earlier-published PTF (PTF-4), respectively. Our study proposed a potential model to improve the performance of BD_fine prediction, and the resultant topsoil BD_fine and SOC stock datasets at 0–20 cm across the EU and UK enable more precise soil hydrological and biological modeling at a continental scale.