the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
European topsoil bulk density and organic carbon stock database (0–20 cm) using machine-learning-based pedotransfer functions
Songchao Chen
Zhongxing Chen
Xianglin Zhang
Zhongkui Luo
Calogero Schillaci
Dominique Arrouays
Anne Christine Richer-de-Forges
Zhou Shi
Soil bulk density (BD) serves as a fundamental indicator of soil health and quality, exerting a significant influence on critical factors such as plant growth, nutrient availability, and water retention. Due to its limited availability in soil databases, the application of pedotransfer functions (PTFs) has emerged as a potent tool for predicting BD using other easily measurable soil properties, while the impact of these PTFs' performance on soil organic carbon (SOC) stock calculation has been rarely explored. In this study, we proposed an innovative local modeling approach for predicting BD of fine earth (BDfine) across Europe using the recently released BDfine data from the LUCAS Soil (Land Use and Coverage Area Frame Survey Soil) 2018 (0–20 cm) and relevant predictors. Our approach involved a combination of neighbor sample search, forward recursive feature selection (FRFS), and random forest (RF) models (local-RFFRFS). The results showed that local-RFFRFS had a good performance in predicting BDfine (R2 of 0.58, root mean square error (RMSE) of 0.19 g cm−3, relative error (RE) of 16.27 %), surpassing the earlier-published PTFs (R2 of 0.40–0.45, RMSE of 0.22 g cm−3, RE of 19.11 %–21.18 %) and global PTFs using RF models with and without FRFS (R2 of 0.56–0.57, RMSE of 0.19 g cm−3, RE of 16.47 %–16.74 %). Interestingly, we found that the best earlier-published PTF (R2 = 0.84, RMSE = 1.39 kg m−2, RE of 17.57 %) performed close to the local-RFFRFS (R2 = 0.85, RMSE = 1.32 kg m−2, RE of 15.01 %) in SOC stock calculation using BDfine predictions. However, the local-RFFRFS still performed better (ΔR2 > 0.2) for soil samples with low SOC stocks (< 3 kg m−2). Therefore, we suggest that the local-RFFRFS is a promising method for BDfine prediction, while earlier-published PTFs would be more efficient when BDfine is subsequently utilized for calculating SOC stock. Finally, we produced two topsoil BDfine and SOC stock datasets (18 945 and 15 389 soil samples) at 0–20 cm for LUCAS Soil 2018 using the best earlier-published PTF and local-RFFRFS, respectively. This dataset is archived on the Zenodo platform at https://doi.org/10.5281/zenodo.10211884 (S. Chen et al., 2023). The outcomes of this study present a meaningful advancement in enhancing the predictive accuracy of BDfine, and the resultant BDfine and SOC stock datasets for topsoil across the Europe enable more precise soil hydrological and biological modeling.
- Article
(13778 KB) - Full-text XML
- BibTeX
- EndNote
Soil plays a pivotal role in supporting ecosystems and sustaining life on our planet (Rabot et al., 2018). Its physical properties are crucial for various disciplines such as agriculture, environmental science, and land management. Among these properties, soil bulk density (BD) holds particular significance as it serves as a fundamental indicator of soil health, structure, and water-holding capacity. BD directly influences vital factors like plant growth, nutrient availability, and overall soil quality (Dam et al., 2005; Chen et al., 2018; Schillaci et al., 2021). Additionally, BD plays a crucial role in computing the stock of water, chemical elements (e.g., soil organic carbon, SOC), or compounds by soil surface unit or soil volume unit, making it even more essential in soil studies. Nonetheless, the uncertainty in SOC stock estimates arises due to the variations in methods used to substitute for missing BD data (Benites et al., 2007; Dawson and Smith, 2007; Wiesmeier et al., 2012; Z. Chen et al., 2023). It is important to acknowledge that BD in topsoil exhibits considerable variations across different geographical regions due to factors like diverse soil types, climate conditions, vegetation cover, and land cover patterns (Hollis et al., 2012; Lark et al., 2014; Li et al., 2019). These regional disparities underscore the need for a comprehensive understanding of BD in soil research and its implications for various aspects of ecosystem functioning and management.
Characterizing the spatial distribution of BD across a diverse and extensive continent like Europe presents a complex challenge (Chen et al., 2018; Nasta et al., 2020; Palladino et al., 2022; Panagos et al., 2024). Conventional soil sampling and laboratory analyses are time-consuming, costly, and impractical at a broad scale (Makovníková et al., 2017). In response to this challenge, the development of pedotransfer functions (PTFs) has emerged as a powerful approach (Van Looy et al., 2017). PTFs are mathematical models that estimate soil properties, such as BD, based on readily available and easily measurable soil data (e.g., SOC, clay, silt, and sand). These functions serve as invaluable tools for predicting soil properties at unvisited locations, facilitating regional soil mapping, and enhancing our understanding of soil dynamics across vast areas (Chen et al., 2018; Schillaci et al., 2021; Palladino et al., 2022). Furthermore, the incorporation of globally available predictor variables, such as topography and land cover, showed promise in enhancing the effectiveness and applicability of PTFs for gap-filling of BD data (Ramcharan et al., 2017; Bondi et al., 2018; Patton et al., 2019).
Table 1Summary of previous studies on using PTFs for BD prediction across scales. R2 indicates the determination coefficient.
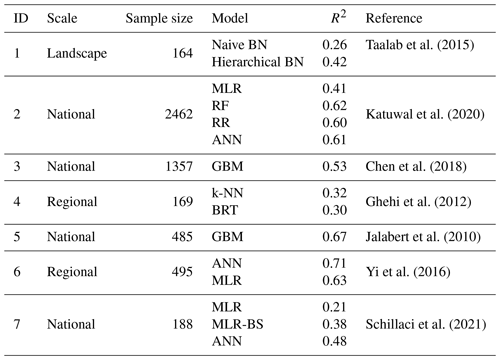
MLR is for multiple linear regression, RF is for random forest, RR is for regression rule, ANN is for artificial neural network, GBM is for generalized boosted model, BRT is for boosted regression tree, BN is for Bayesian network, k-NN is for k nearest neighbor, and MLR-BS is for multiple linear regression (stepwise variable selection).
In the early stage, PTFs predominantly employed regression techniques due to their simplicity (Gupta and Larson, 1979; Rawls and Brakensiek, 1985). However, with advancements in science and technology, a wide range of models have been developed for deriving PTFs, particularly for continuous predicted variables. These methods encompass linear regression, generalized linear models, generalized additive models, regression trees, artificial neural networks, support vector machines, gradient boosted models, and random forests (RFs) (Van Looy et al., 2017; Chen et al., 2018). The utilization of these advanced techniques has substantially improved the accuracy of BD prediction (Table 1).
PTFs have emerged as an alternative approach to address the scarcity of BD data (Van Looy et al., 2017). They have been implemented and tested in diverse regions and countries, providing a practical and cost-effective means for predicting BD using readily available soil properties. However, it is noteworthy that the majority of previous studies utilizing machine learning (ML) and PTFs for BD prediction have been conducted at regional or national scales, with limited research focusing on the intercontinental scale (Taalab et al., 2015; Shiri et al., 2017; Katuwal et al., 2020). Despite the accomplishments of PTFs in BD estimation, a gap emerges when transitioning to global modeling (a fixed model to predict all the unknown samples) endeavors. The reliance on global models, while useful in capturing broad patterns, often faces constraints in delivering accurate predictions at finer scales (Gupta et al., 2018). These global models may fail to account for the nuanced spatial and environmental variations that play a pivotal role in determining BD across different landscapes. While numerous studies have harnessed ML-based PTFs (ML-PTFs) to improve the model performance of BD at national and regional levels, the expansion of these methodologies to encompass continental contexts remains relatively limited (Nasta et al., 2020; Schillaci et al., 2021; Palladino et al., 2022). This gap underscores the need for a modeling approach that bridges the gap between broad-scale global modeling and the context-specific requirements of diverse regions and ecosystems (Wang et al., 2024). This is where the concept of local modeling steps in. The local model adopts a dynamic modeling strategy: it firstly selects a part of similar samples close to each unknown sample in the predictor space, and then it fits a predictive model using the selected similar samples (not the entirety of the data). Since the selected similar samples vary for each unknown sample, the corresponding local model is different from others. A local modeling strategy enables the consideration of environmental relevance by clustering data under similar environmental conditions (i.e., in the present case, similar predictors feature space, including soil properties, elevation, land cover, and climate conditions), which aids in constructing specialized PTFs that capture soil–environment relationships (Nocita et al., 2014; Chen et al., 2018). Thus, there is a compelling need for further investigations of and developments in local modeling techniques to improve BD predictions. Furthermore, despite the wide use of PTFs in predicting BD in SOC stock calculations from continental to global scales, how the performances (e.g., R2, root mean square error, relative error) of PTF-based BD prediction impact the quality of SOC stock remains poorly explored (Cotrufo et al., 2019; Augusto and Boča, 2022; Wang et al., 2022; De Rosa et al., 2023).
To address the aforementioned issues, we investigated an RF model in combination with variable selection and a local modeling strategy to evaluate the potential of different PTFs in BD prediction, as well as in SOC stock calculation. The main objectives of this study are as follows:
-
to compare the performances of earlier-published PTFs and ML-PTFs for BD prediction
-
to evaluate the potential of local modeling strategies for BD prediction
-
to investigate the impact of PTF-based BD prediction on the accuracy of SOC stock calculation.
2.1 Soil data
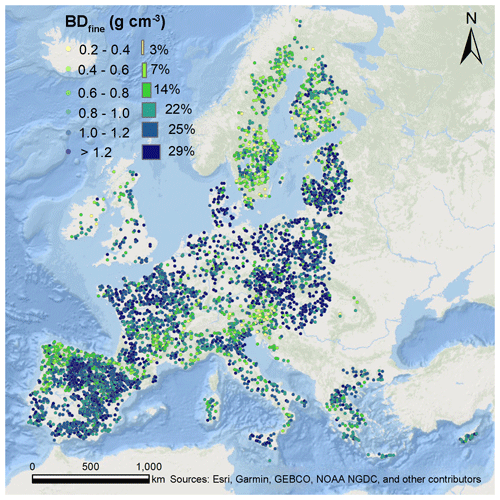
The soil data were compiled from the Land Use and Coverage Area Frame Survey Soil (LUCAS Soil) campaigns conducted in 2009, 2015, and 2018 (Fernández-Ugalde et al., 2022; Panagos et al., 2022). The survey encompassed a stratified random sampling approach, which identified approximately 20 000 topsoil sampling locations across the European Union (EU) and the United Kingdom (UK) for each campaign. At each sampling site (circle of 4 m diameter plot), five topsoil samples (0–20 cm) were collected after the removal of the litter layer, and the land cover (LC) was recorded. These samples were then combined into a bulked composite topsoil sample for analysis. Subsequently, all topsoil samples underwent air-drying and sieving to less than 2 mm. Standard laboratory analysis was conducted in an accredited laboratory (Kecskemét, Hungary), including particle size fractions (clay content, silt content, sand content, %), coarse fragments (mass fraction, %/100), BD (whole mass, g cm−3), pH (in water), SOC content (g kg−1), carbonates (CaCO3, g kg−1), total nitrogen (N, g kg−1), extractable potassium (K, mg kg−1), and cation exchange capacity (CEC, ). For more comprehensive information about LUCAS Soil 2009/2015/2018, we refer the reader to Orgiazzi et al. (2022). In the LUCAS Soil 2018 survey, topsoil sampling was conducted across all EU Member States and the UK, employing the identical set of 25 947 locations that were targeted during the 2015 survey (Fernández-Ugalde et al., 2022). However, due to the absence of particle size fractions in LUCAS Soil 2018, we resorted to using the data from LUCAS Soil 2009/2015 according to the unique identifier soil ID (Panagos et al., 2022). To ensure the reliability of the data, we excluded samples with soil particle fractions recorded as 0. Finally, 5163 topsoil samples were retained for further analysis (Fig. 1). In the following parts of the article, we define BDsample as the whole soil mass : volume ratio and BDfine as the fine-earth mass : volume ratio.
Since BDsample was measured for the whole mass and CF was measured as a mass fraction (CFmassfraction) in part of the topsoil samples of the LUCAS Soil 2015/2018, they cannot be used directly to accurately calculate SOC stock. Note that, if the mass of the fine fraction has been measured and recorded (as the total volume of the sample is known), the SOC stock can be calculated directly (Poeplau et al., 2017). However, in numerous locations, neither the mass of the fine fraction nor BDsample was measured. This is why we needed to estimate and use BDfine and CFvolumefraction in order to calculate SOC stocks where BDsample was missing (Poeplau et al., 2017). To this aim, we used a recently released dataset for BDfine and CFvolumefraction by Pacini et al. (2023) based on BDsample and CFmassfraction from LUCAS Soil 2018.
2.2 Predictor variables related to relief, climate, and land cover
The elevation (ELE) was derived from the Shuttle Radar Topography Mission (SRTM) 1 km digital elevation model (Farr et al., 2007). Climatic data, including mean annual precipitation (MAP) and mean annual temperature (MAT), were acquired from the WorldClim version 2 at 1 km resolution (Fick and Hijmans, 2017). The Global-PET dataset at 1 km resolution was used to extract potential evapotranspiration (PET) and aridity index (AI) (Zomer et al., 2022). The land cover (LC) was directly derived from the records of LUCAS Soil 2018 during the soil sampling campaign.
Table 2Summary of four earlier-published PTFs defined in the literature.
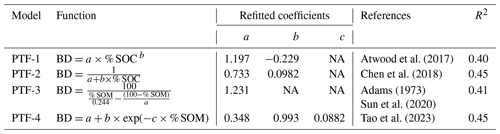
BD is for bulk density; depending on the authors cited in references, BD has been considered to be the BD of the fine fraction (BDfine) or the BD of the whole sample (BDsample) (both expressed in g cm−3); here, the refitted coefficients correspond to BDfine. SOM is for soil organic matter content (% in soil mass). SOC is for soil organic carbon content (% in soil mass). NA: not available.
2.3 Earlier-published PTFs
We evaluated four earlier-published PTFs that have been widely used to estimate BDsample or BDfine in previous studies at both local and broad scales (Adams, 1973; Atwood et al., 2017; Chen et al., 2018; Sun et al., 2020; Tao et al., 2023). For PTF-3 and PTF-4, soil organic matter (SOM) content was determined by the conversion factor of 1.724 using SOC content. In the present study, we used these PTFs to estimate BDfine. The parameters in these PTFs were refitted by the Levenberg–Marquardt nonlinear least-square method available in the minpack.lm R package based on our data (Bates and Watts, 1988; Zhu et al., 1997; Elzhov et al., 2015). These refitted parameters of PTFs are present in Table 2.
Table 3The variables used in RFFull and RFFRFS. For RFFRFS; the order of the variables is by descending importance. RFFull uses all potential predictors, even if they may be redundant of multi-collinear (typical case of the use of clay, silt, and sand contents together). RFFRFS applies FRFS, thus eliminating both multi-collinearity and irrelevant predictor variables (e.g., one particle size fraction (sand content) is left out). The abbreviations are detailed as follows: SOC is for soil organic carbon content, CEC is for cation exchange capacity, AI is for aridity index, PET is for potential evapotranspiration, MAP is for mean annual precipitation, MAT is for mean annual temperature, ELE is for elevation, and LC is for land cover. Clay, silt, sand, and CaCO3 are expressed in %; pH is pH in a 1:2.5 soil:water mixture.

2.4 Global ML-PTFs
To compare with earlier-published PTFs, we used a random forest (RF) model to construct global ML-PTFs for predicting BDfine. RF is an ensemble learning method that aggregates predictions from multiple decision trees to obtain the final estimates of the target variable. In growing a decision tree, a random subsample of data is selected from the verification dataset, and a set of random predictor variables is used for splitting the subsampled data. Two parameters, ntree and mtry, were optimized by 10-fold cross-validation. Here, 15 predictor variables, such as sand content, silt content, clay content, SOC content, and ELE (Table 3), were used to build the global RF model.
Furthermore, we adopted a recently proposed variable selection method, namely forward recursive feature selection (FRFS), to reduce the number of predictor variables while not losing model performance (Xiao et al., 2022a; Zhang et al., 2023). FRFS employs a forward selection strategy, involving the following sequential steps: (1) initially, an RF model is fitted using all the n predictors, and their variable importance is calculated; (2) the most important predictor (only one) is selected to create an initial model, and its performance is assessed using 10-fold cross-validation with a single predictor in the pool; (3) subsequently, a series of models are constructed using two predictors, where the first predictor is chosen from the pool, and the second predictor is selected from the remaining predictors. The model performances are evaluated, and the model with the best performance is recorded; (4) the pool of predictors is then updated based on the predictors from the best-performing model in the previous step; (5) the process is iteratively repeated, progressively increasing the number of predictors from 3 to n. Ultimately, the predictors used in the model with the best performance are selected to form the final predictive model, as detailed in the work of Xiao et al. (2022a). The R script for implementing FRFS is accessible at https://doi.org/10.5281/zenodo.7141020 (Xiao et al., 2022b). In this study, FRFS was applied to select the most relevant predictors constructing the predictive models (Table 3).
For clarity, in global modeling, we refer to the RF model using the full variables as global-RFFULL and the combination of the RF model with FRFS as global-RFFRFS.
2.5 Local ML-PTFs
The development of local ML-PTFs consists of four steps: (1) use the Mahalanobis distance to calculate the distances of predictor variables between each sample to be predicted and all the samples in the database; (2) select k nearest-neighbor samples to fit an RF model for each unknown sample; (3) predict the BDfine for each unknown sample using relevant RF models. Since the number of nearest-neighbor samples (k) is an important parameter in the local model, we evaluated its effect on the model performance by testing k from 20 to 700 (20, 40, 60, 80, 100, 150, 200, 250, 300, 350, 400, 450, 500, 550, 600, 650, 700).
For clarity, we refer to the local modeling using the full variables as local-RFFULL, and we refer to the combined use of the RF model and variables selected by global-RFFRFS as local-RFFRFS.
2.6 Model evaluation
Due to the large sample size, a single random split is stable compared to k-fold cross-validation or a repeated random split (Chen et al., 2021). Therefore, we used a random split (80 % for calibration and 20 % for validation) to assess the model performance of earlier-published PTFs and ML-PTFs. It is important to note that the same validation set was used to evaluate earlier-published PTFs and ML-PTFs. The root mean square error (RMSE), determination coefficient (R2), and relative error (RE) were used as performance indicators in the validation set (Chen et al., 2022). These indices are defined following Eq. (1), (2), and (3):
where n represents the number of observations, Oi and Pi are the observed and predicted BDfine for observation i, and is the mean of the observed BDfine. A good model has an RMSE and RE close to 0 and also higher R2 close to 1.
2.7 The build-up of extended BDfine and SOC stock datasets for topsoil in Europe
Since only part of LUCAS 2015/2018 had soil particle fractions and CaCO3, we used the unique sample ID to link the missing soil particle fractions and CaCO3 using LUCAS Soil 2009 for the same sampling sites. This operation is reasonable since soil particle fractions and CaCO3 will not have experienced a notable change within a decade. The SOC stock (kg m−2) at a depth of 0–20 cm for LUCAS Soil 2018 was calculated by the SOC content (g kg−1), BDfine (g cm−3), CFvolumefraction (), and depth (20 cm) as in Eq. (4) (Poeplau et al., 2017).
3.1 Statistics of BDfine and its correlation with predictor variables
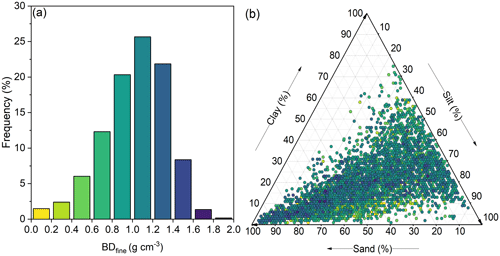
Figure 2 illustrates the histogram of BDfine values and their distribution in a ternary soil texture triangle. The dataset consists of 5163 topsoil samples, with BDfine ranging from 0.20 to 1.89 g cm−3. The topsoil sample with the lowest BDfine (0.20 g cm−3) was collected from a pine-dominated mixed woodland with an SOC content greater than 137 g kg−1. In contrast, the topsoil sample with the highest BDfine (1.89 g cm−3) was sampled from a sandy soil (sand and clay of 65 % and 11 %, SOC content of 31.9 g kg−1) in cropland (common wheat). Approximately half of the topsoil samples exhibited BDfine between 0.8 and 1.4 g cm−3, while less than 10 % of the topsoil samples had BDfine exceeding 1.4 g cm−3. As shown in the soil texture triangle, the selected topsoil samples covered a wide range of soil texture classes.

Figure 3Correlation plot of BDfine and predictors. The sizes of the circles represent the magnitudes of the correlation, and light and dark colors represent negative and positive correlations, respectively. The abbreviations are detailed as follows: BDfine is for bulk density of fine earth, CEC is for cation exchange capacity, SOC is for soil organic carbon content, AI is for aridity index, PET is for potential evapotranspiration, MAP is for mean annual precipitation, MAT is for mean annual temperature, ELE is for elevation, and LC is for land cover.
Figure 3 depicts the correlation matrix between BDfine and 15 predictor variables. BDfine exhibited positive correlations with pH and MAT, with correlation coefficients (r) greater than 0.25. On the other hand, BDfine showed notably high negative correlations with most of the other predictors. The most influential negative predictor was SOC content (r = −0.62), followed by N (r = −0.56) and CaCO3 (r = −0.33). Note that BDfine under various LC classes exhibited significant differences in terms of mean BDfine of 1.16, 1.00, 0.78, and 1.02 g cm−3 for cropland, grassland, woodland, and others, respectively.
3.2 Selection of predictor variables
Table 3 presents the predictor variables utilized in the RF model for predicting BDfine. In the global-RFFULL model, 15 predictor variables were included, namely clay content, silt content, sand content, pH, SOC content, CaCO3, N, K, CEC, AI, PET, ELE, MAP, MAT, and LC. On the other hand, the global-RFFRFS identified a subset of eight predictor variables by means of FRFS that were deemed to be most important for BDfine prediction. These selected predictor variables, ranked in descending order of importance, were SOC content, N, pH, PET, MAP, LC, AI, and MAT.
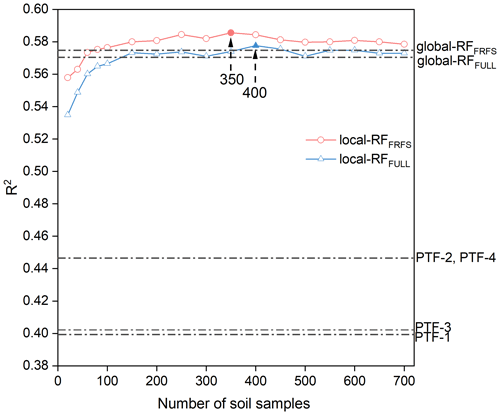
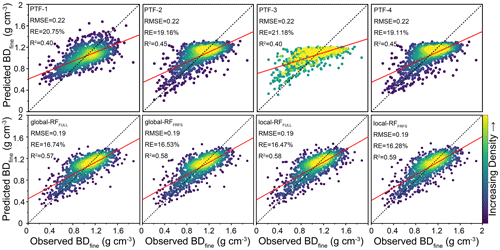
Figure 4Model performance indicator (R2) of earlier-published PTFs and ML-PTFs in BDfine prediction. The performances of local RF models (local-RFFULL and local-RFFRFS) change with the number of soil samples used for local modeling.
3.3 Comparison of ML-PTFs and earlier-published PTFs in BDfine prediction
In this study, we compared ML-PTFs with four earlier-published PTFs in BDfine prediction (Figs. 4 and 5). The earlier-published PTFs had model performances with an RMSE of 0.22 g cm−3, R2 of 0.40–0.45, and RE of 19.11 %–20.75 %. The global-RF models had higher model performances, with an RMSE of 0.19 g cm−3, R2 between 0.57 and 0.58, and RE of 16.53 %–16.74 % for global-RFFULL and global-RFFRFS, respectively, though the latter performed slightly better (see R2 values in Fig. 4). As for local models, it was clear that the model performance showed an increasing trend when the number of neighbor samples increased, and some fluctuations were observed after the model performance reached a plateau. The number of neighbor samples was optimized at 350 and 400 for local-RFFRFS and local-RFFULL, respectively. Compared to global modeling, the best local-RFFRFS and local-RFFULL performed slightly better with R2 of 0.59–0.57 and RE of 16.28 %–16.47 %.
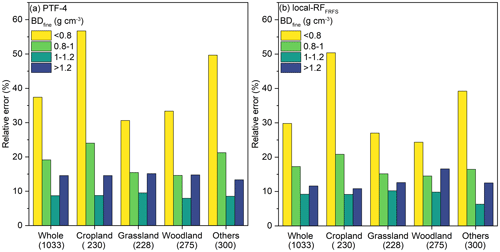
Figure 6The variations in RE related to BDfine ranges of values (< 0.8, 0.8–1, 1–1.2, and > 1.2 g cm−3) and land covers using PTF-4 (a) and local-RFFRFS (b). The number under the land cover is the corresponding topsoil sample size.
The summary of RE variations under different BDfine levels and land covers using best earlier-published PTF (PTF-4) and ML-PTF (local-RFFRFS) is shown in Fig. 6. The results indicated that local-RFFRFS (RE of 29 %) performed much better than PTF-4 (RE of 37 %) for the topsoil with low BDfine (< 0.8 g cm−3). The improvement in RE for other BD levels was rather limited (ΔRE of 1 %–3 %). The highest RE (30 %–57 % for PTF-4, 25 %–50 % for local-RFFRFS) was found for topsoil with low BDfine for the whole validation set and each land cover. Across land covers, the RE generally decreased greatly (15 %–24 % for PTF-4, 14 %–20 % for local-RFFRFS) for topsoil with low–median BDfine (0.8–1 g cm−3) and then decreased to its lowest (7 %–9 % for both PTF-4 and local-RFFRFS) for topsoil with median–high BDfine (1–1.2 g cm−3). A slight increase in RE (14 %–16 % for PTF-4, 11 %–17 % for local-RFFRFS) was observed for topsoil with high BDfine (> 1.2 g cm−3) for all the land covers. Among different land covers, the cropland had the greatest RE for topsoil with low and low–median BDfine, followed by others, woodland, and grassland. For topsoil with median–high and high BDfine, a similar RE was found for all the land covers. Overall, the RE for both PTF-4 and local-RFFRFS showed the worst performances for low BDfine, but the results were always better for local-RFFRFS, except for woodlands with BDfine > 1, where the RE was slightly better for PTF-4.
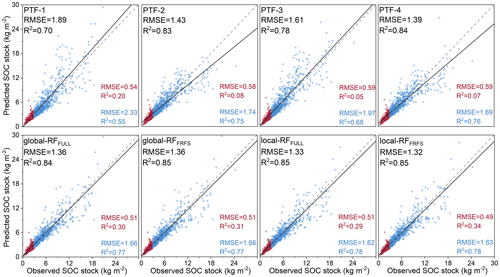
Figure 7Scatter plots of SOC stock predictions by earlier-published PTFs and ML-PTFs along with model performance indicators (RMSE, R2, and RE). The red points represent topsoil samples with SOC stock < 3 kg m−2, while the blue points represent topsoil samples with SOC stock ≥ 3 kg m−2. Note that observed SOC stock is computed using SOC content, CFvolumefraction, and BDfine observations, and while predicted SOC stock is computed using SOC content observations, BDfine predictions and CFvolumefraction are transformed from CFmassfraction using BDfine predictions, as suggested by Pacini et al. (2023).
3.4 Comparison of ML-PTFs and earlier-published PTFs in SOC stock calculation
We investigated how using BDfine estimated by PTFs impacted the accuracy of SOC stock calculation (Fig. 7). We found that SOC stock calculation using BDfine predictions from four earlier-published PTFs resulted in a good performance, with an RMSE of 1.39–1.89 kg m−2, R2 of 0.70–0.84, and RE of 17.57 %–19.46 %. Meanwhile, the performance indicators of SOC stock calculation using BDfine prediction (RMSE of 1.32–1.36 kg m−2, R2 of 0.84–0.85, RE of 15.01 %–15.41 %) always exhibited slightly better performances than the earlier-published PTFs. However, the performances of the best earlier-published PTF (PTF-4) were rather similar to those of the local-RFFRFS. Overall, the performances of the local-RFFRFS were the best.
3.5 Summary of the extended European topsoil BDfine and SOC stock database
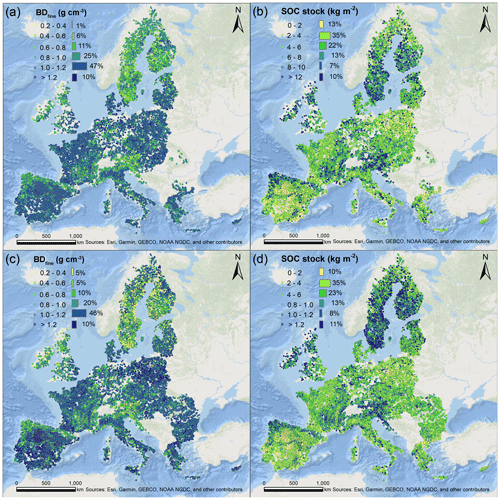
To enlarge the topsoil BDfine and SOC stock database (0–20 cm) for Europe, we refitted the best ML-PTF (local-RFFRFS) and the best earlier-published PTF (PTF-4) using all 5163 topsoil samples to predict topsoil samples without BDfine, and then we calculated SOC stock, which resulted in 15 389 and 18 945 topsoil sample predictions for the extended database, respectively (fewer topsoil samples had all the required variables for the use of local-RFFRFS). As shown in Fig. 8, these extended topsoil BDfine and SOC stock databases are more regularly distributed across the EU and UK compared to the points in Fig. 1. In the EU and UK, BDfine in topsoil was primarily distributed within 1.0–1.2 g cm−3 (46 %–47 %), while the SOC stock in topsoil was mainly comprised between 2 and 4 kg m−2.
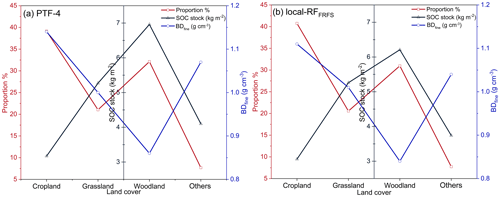
Figure 9Variations in topsoil BDfine and SOC stock under different land covers using PTF-4 (a) and local-RFFRFS (b).
As shown in Fig. 9, in the database created by local-RFFRFS (15 389 topsoil samples), the topsoil samples under cropland had the highest median BDfine of 1.11 g cm−3, while woodland exhibited the lowest median BDfine at 0.84 g cm−3. Conversely, woodland had the highest median SOC stock at 6.21 kg m−2, while cropland showed the lowest median SOC stock at 3.06 kg m−2. As for the database built on PTF-4 (18 945 topsoil samples), cropland also had the highest median BDfine at 1.14 g cm−3, while woodland exhibited the lowest median BDfine at 0.86 g cm−3. In contrast, the SOC stock under woodland presented the highest median SOC stock at 6.96 kg m−2, while cropland had the lowest median SOC stock at 3.17 kg m−2.
4.1 The superiority of ML-PTFs in BDfine prediction
In this study, using the LUCAS Soil and 15 predictor variables, we compared the model performance of four earlier-published PTFs and four ML-PTFs for BDfine in topsoil (0–20 cm). Four earlier-published PTFs showed a moderate model performance with R2 of 0.40–0.45, which is close to a recently developed Hollis-type PTF (R2 of 0.41, Hollis et al., 2012) that was refitted with LUCAS Soil 2018 data (De Rosa et al., 2023). Our results underscored the efficacy of ML-PTFs in successfully predicting BDfine at a continental scale, yielding a substantial R2 ranging from 0.57 to 0.59. This indicates that, when adding more relevant predictor variables (e.g., N, pH, PET, MAP) to the topsoil database, ML-PTFs is a better choice for improving BDfine prediction than earlier-published PTFs based on algebraic equations. Otherwise, earlier-published PTFs are still the best choice to impute the missing data due to their simplicity (Van Looy et al., 2017).
In addition to global PTFs that use all the soil samples, we introduced the local modeling strategy in PTFs, which searched similar samples first and then built the relevant PTF for each unknown sample dynamically. Generally, the model performance of local PTFs (local-RFFULL and local-RFFRFS) for BDfine prediction continuously improved with the increasing number of neighbor samples, and then it reached a plateau when the number of neighbor samples reached approximately 350 to 400 (Fig. 4). Compared to the global PTFs (4500 soil samples), the sizes of local PTFs were much smaller (350–400 soil samples) with slightly better model performance. Therefore, the comparison between global PTF and local PTF performances shows that local PTFs can improve the efficiency of imputing missing data using a large soil database (Padarian et al., 2019; Sanderman et al., 2020).
In comparison to the earlier-published PTFs that were refitted using our data, the local-FRFRFS model substantially improved model performance in BDfine prediction (ΔR2 of 0.14–0.19). Our results suggest that ML-PTFs performed much better than earlier-published PTFs for BDfine prediction. This resulted from the fact that most of the ML models are able to handle nonlinear and complex relationships between the predictor variables and the response variable, thereby improving predictions compared to those of earlier-published PTFs (Katuwal et al., 2020; Palladino et al., 2022). Meanwhile, the earlier-published PTFs typically rely solely on SOC or SOM content for BDfine prediction. This approach maintains model simplicity but overlooks readily available predictor variables such as particle size fractions, MAT, and MAP, which are also pertinent to BDfine prediction (Abdelbaki, 2018). Despite the high diversity in landscapes and climates at a continental scale, the proposed local-FRFRFS model demonstrated similar or even superior performance compared to the ML-PTFs conducted at regional and national scales (Table 1).
Looking into the RE for topsoil under different BDfine levels (Fig. 6), it is clear that the best-fitted PTFs (PTF-4 and local-RFFRFS) had the highest REs for topsoil with low BDfine (< 0.8 g cm−3) despite the fact that local-RFFRFS performed better. This partly results from the low BDfine required to calculate the RE because the BDfine value is used as the reference 100 % value in RE calculation. This is also likely due to the general trend of broad-scale predictions smoothing the variability and overestimating the low values and underestimating the high values, whatever the predicted variable is (e.g., Tifafi et al., 2018; Lemercier et al. 2022; Richer-de-Forges et al., 2023). Most importantly, many low BDfine observations are probably linked to large voids, resulting in a large porosity, especially under disturbed topsoil. This explains why cropland topsoil exhibited such a large RE, likely due to the effect of soil tillage which cannot be predicted by our predictor variables. This can also explain the decreasing trend in RE with the increase in BDfine up to 1.2 g cm−3, whereas, for the topsoil with high BD (> 1.2 g cm−3), both local-RFFRFS and PTF-4 showed a slight increase in RE. Overall, the RE values might appear to be a bit deceiving if we compare them to the accuracy that one may wish for in monitoring changes in BDfine – for example, as an indicator of compaction. We must state that this is clearly out of the scope of this study, which is intended to provide a wide database that can be used for broad-scale modeling.
4.2 Performance of FRFS and variable importance in BDfine prediction by ML-PTFs
We reduced the number of predictor variables in the RF model from 15 to 8 using the FRFS algorithm, and the model performance of global-RFFRFS for BDfine using FRFS-selected variables was higher than that of global-RFFULL using full variables (Table 3). Though the local-RFFRFS (R2 of 0.59) only had marginal superiority over the local-RFFULL model (R2 of 0.58), it facilitated the reduction of variables, consequently enhancing prediction efficiency (Figs. 4 and 5). This outcome validates the capacity of FRFS to simplify the model complexity while concurrently enhancing its predictive accuracy (Xiao et al., 2022a; Liu et al., 2023; Zhang et al., 2023; Hu et al., 2024). Being a useful tool for gap-filling the missing data, an ideal PTF requires both high parsimony and good fit. If the developed PTF needs too many predictors variables, its practical applicability would be limited as much fewer soil samples have all the required predictor variables.
4.3 The build-up of extended BDfine and SOC stock datasets in Europe
We used the BDfine predictions from eight PTFs together with CFvolumefraction to calculate the SOC stock. The results showed that the model performances of SOC stock (R2 of 0.70–0.85) were much higher than those of BDfine (R2 of 0.40–0.59) (Figs. 5 and 7). This can be explained by the interdependence between BDfine and SOC content. For instance, a soil sample with a high SOC content commonly has a large pore space due to the large amount of organic matter, leading to a low BDfine (Perie and Ouimet, 2008; Chen et al., 2018). As shown in Fig. 7, high SOC content and BDfine were always underestimated, while the low SOC content and BDfine were overestimated. By multiplying these two negatively correlated variables, the predicted SOC stock could be closer to the observed SOC stock as the overestimation (underestimation) of BDfine can counterbalance the underestimation (overestimation) of SOC content, resulting in better model performance than BDfine. It is interesting to note that the model performances of the best earlier-published PTFs (PTF-4, R2 of 0.84) and ML-PTFs (local-RFFRFS, R2 of 0.85) were quite close in terms of SOC stock prediction. This indicated that the improvement of BDfine prediction by ML-PTFs did not impact the accuracy of SOC stock prediction. Looking into the scatter plots shown in Fig. 5, we can observe that the ML-PTFs performed much better than earlier-published PTFs for topsoil samples with high BDfine (and low SOC content), while a limited difference was found for soil samples with low BDfine (and high SOC content). Compared to earlier-published PTFs, ML-PTFs tended to predict SOC stock better for topsoil samples with low SOC stock (< 3 kg m−2), while similar model performances can be found in topsoil samples with high SOC stocks (≥ 3 kg m−2), which is evident in Fig. 5. As a result, the best earlier-published PTF (PTF-4) performed quite similarly to the best ML-PTF (local-RFFRFS) when considering the topsoil samples with a wide range in terms of SOC stock. This last result suggests that earlier-published PTFs could be useful default tools in estimating BDfine which is subsequently used for SOC stock calculation. One of the advantages of these earlier-published PTFs is their simplicity; another obvious advantage is that they require fewer training soil samples than ML-PTFs to be fitted and validated. Otherwise, if enough data are available, ML-PTFs are suggested for more accurate BDfine prediction, especially for regions with low SOC stocks, such as dry land regions in Spain and Italy (Maestre et al., 2021; De Rosa et al., 2023; Wang et al., 2023).
4.4 Limitations and perspectives
It is essential to acknowledge that our developed PTFs for BDfine prediction were constructed based on LUCAS Soil data (0–20 cm), confining their applicability to topsoil within the EU and UK (Orgiazzi et al., 2022, Panagos et al., 2022). However, the potential of their extrapolation capability to other regions or to deep soil (> 20 cm) necessitates further evaluation. As more soil data become available from diverse regions, as well as for deep soil (Lal, 2018; Tautges et al., 2019; Batjes et al., 2020; Yost and Hartemink, 2020; Palmtag et al., 2022; Armas et al., 2023), the proposed methodology can be further used to update the PTFs, thereby broadening their area of applicability (Chen et al., 2018; Meyer and Pebesma, 2021). In addition, when a depth-specific soil BDfine database is available, it will be important to develop depth-explicit ML-PTFs to account for the effects of climate and topography on BDfine at depths.
We acknowledge that our use of PTF-3 and PTF-4 is based on measured SOC contents and on a fixed Van Bemmelen factor (SOM = 1.724 × SOC, Sprengel, 1826; Van Bemmelen, 1890). One good reason to use this factor is that it enables a comparison with most of the studies predicting BDfine using SOC and other soil properties. One pitfall is that we know that the conversion factor from SOC to SOM is not constant (Pribyl, 2010). However, this conversion factor was only used for PTF-3 and PTF-4. Considering the equations used, changing this conversion factor for PTF-4 has no consequence on the predicted BDfine or on the model performance of the PTF for BDfine prediction. Changing it for PTF-3 will lead to lower performance. We have no clear indication that we ought to try to adapt the Van Bemmelen factor to the pedological context (or to the effect of SOC on BDfine) when we use fixed regressions such as PTF-3 and PTF-4. One advantage of ML-PTFs, and especially of local ML-PTFs, is that they can take into account interactions between soil properties. Therefore, the importance of SOC likely varies depending other local controlling factors such as clay content, climate, or even the nature of the organic compounds, which could explain the strong effect of N. In other words, ML-PTFs were able to partially compensate for the effect of using a fixed conversion factor between SOC and SOM. It should be noted that the BDfine and CFvolumefraction used in this study have been transformed from BDsample and CFmassfraction by Pacini et al. (2023), which certainly introduced some uncertainty. However, for topsoil samples with CF close to 0, the uncertainty from data transformation is rather low. Since many cropland soils have CF close to 0, and because they are the most sensitive to threats, the proposed PTFs for BDfine prediction would be helpful.
Another possible source of error is linked to re-allocating some measured values from one LUCAS Soil sampling campaign to another one. Indeed, BD (whether BDfine or BDsample) is highly variable in space and time, and coarse fragments and SOC are highly variable in space. The location of sampling may change slightly between LUCAS Soil campaigns for various reasons, and the instructions recommend a distance of < 100 m (Fernández-Ugalde et al., 2017). This latter case has no reason to induce a systematic bias. However, it increases the uncertainty (Munera-Echeverri et al., 2022). Finally, soils containing large amounts of large rocks are clearly excluded from the LUCAS Soil protocol; therefore, one should keep this in mind so as to not extrapolate BDfine and SOC stock predictions to rocky soils.
If one wants to use PTF-based BDfine prediction to detect SOC stock changes, the impact of the performance of PTFs on the accuracy of SOC stock calculation remains unclear since the equivalent soil mass approach also requires BDfine as input (Schrumpf et al., 2011; Wendt and Hauser, 2013). Therefore, this issue could be investigated in future studies. However, the most straightforward and unbiased way to measure SOC stocks by sampling remains the direct determination of the ratio of the fine-earth mass:sample volume by sieving and weighting the fine soil from a sample of known volume.
Most of the predictor variables that we used for ML-PTFs are prone to changes at different timescales. This is the case for all predictor variables derived from climate. Some soil predictor variables (e.g., SOC, pH) can change more or less rapidly under the effect of practices, LC changes, and global changes. Finally, LC can change at any given time, though some effect of past LC may remain for a given time. Though strong perturbations may have an immediate effect on BDfine, the timescales at which most of these predictor variables influence or are just correlated to BDfine remain unclear. This opens the door to further questioning about the processes that govern the importance of these predictor variables to BDfine. Indeed, ML tools can be used as simple predictors at a given time or as tools to raise attention with regard to the possible effects of some controlling factors and their changes and the processes involved in these effects.
All the soil data used in this article are available at the following data sources: (1) Land Use and Coverage Area Frame Survey Soil (LUCAS Soil) 2009 via https://esdac.jrc.ec.europa.eu/content/lucas-2009-topsoil-data (European Commission, 2013; Panagos et al., 2022), (2) LUCAS Soil 2015 via https://esdac.jrc.ec.europa.eu/content/lucas2015-topsoil-data (European Commission, 2020; Fernández-Ugalde et al., 2022), and (3) LUCAS Soil 2018 via https://esdac.jrc.ec.europa.eu/content/lucas-2018-topsoil-data (European Commission, 2022; Panagos et al., 2022); (4) the European topsoil BDfine and SOC stock dataset (0–20 cm) in this paper is available at https://doi.org/10.5281/zenodo.10211884 (S. Chen et al., 2023).
Using the largest extendable soil dataset for Europe, we have developed ML-PTFs for predicting BDfine at 0–20 cm across the EU and UK. In comparison to four earlier-published PTFs, the best ML-PTF, namely local-RFFRFS, exhibited superior performance for BDfine prediction with a percentage increase in R2 at 31.1 %–47.5 % and a percentage decrease in RMSE and RE at 13.6 % and 14.8 %–23.1 %, respectively. When the predicted BDfine was subsequently used for SOC stock calculation, we found that the best earlier-published PTF preformed quite similarly to the best ML-PTF, indicating the fact that earlier-published PTFs would be useful for BDfine prediction when targeting SOC stock calculation. However, for regions with low SOC stock (< 3 kg m−2), ML-PTFs are still recommended due to their high accuracy in SOC stock calculation. Finally, we established two comprehensive pan-European topsoil BDfine and SOC stock databases (0–20 cm) including 15 389 and 18 945 soil samples from LUCAS Soil 2018 using the best ML-PTF (local-RFFRFS) and an earlier-published PTF (PTF-4), respectively. Our study proposed a potential model to improve the performance of BDfine prediction, and the resultant topsoil BDfine and SOC stock datasets at 0–20 cm across the EU and UK enable more precise soil hydrological and biological modeling at a continental scale.
SC, ZC, and XZ compiled the data. SC and ZC performed the analysis and drafted the paper. XZ, ZL, CS, DA, ACRdF, and ZS validated the results and revised the paper. SC acquired the financial support. ZS supervised this work.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims made in the text, published maps, institutional affiliations, or any other geographical representation in this paper. While Copernicus Publications makes every effort to include appropriate place names, the final responsibility lies with the authors.
The authors would like to thank the Joint Research Centre of the European Commission for sharing the LUCAS soil data.
This research has been supported by the National Natural Science Foundation of China (grant no. 42201054).
This paper was edited by Giulio G. R. Iovine and reviewed by Jingyi Huang, Asim Biswas, Ary Bruand, and one anonymous referee.
Abdelbaki, A. M.: Evaluation of pedotransfer functions for predicting soil bulk density for U. S. soils, Ain Shams Eng. J., 9, 1611–1619, https://doi.org/10.1016/j.asej.2016.12.002, 2018.
Adams, W. A.: The effect of organic matter on the bulk and true densities of some uncultivated podzolic soils, J. Soil Sci., 24, 10–17, 1973.
Armas, D., Guevara, M., Bezares, F., Vargas, R., Durante, P., Osorio, V., Jiménez, W., and Oyonarte, C.: Harmonized Soil Database of Ecuador (HESD): data from 2009 to 2015, Earth Syst. Sci. Data, 15, 431–445, https://doi.org/10.5194/essd-15-431-2023, 2023.
Atwood, T. B., Connolly, R. M., Almahasheer, H., Carnell, P. E., Duarte, C. M., Ewers Lewis, C. J., and Lovelock, C. E.: Global patterns in mangrove soil carbon stocks and losses, Nat. Clim. Change, 7, 523–528, https://doi.org/10.1038/nclimate3326, 2017.
Augusto, L. and Boča, A.: Tree functional traits, forest biomass, and tree species diversity interact with site properties to drive forest soil carbon, Nat. Commun., 13, 1097, https://doi.org/10.1038/s41467-022-28748-0, 2022.
Bates, D. M. and Watts, D. G.: Nonlinear regression analysis and its applications: Nonlinear regression analysis and its applications, Wiley Series in Probability and Statistics, John Wiley & Sons, Inc., New York, United States, https://doi.org/10.1002/9780470316757, 1988.
Batjes, N. H., Ribeiro, E., and van Oostrum, A.: Standardised soil profile data to support global mapping and modelling (WoSIS snapshot 2019), Earth Syst. Sci. Data, 12, 299–320, https://doi.org/10.5194/essd-12-299-2020, 2020.
Benites, V. M., Machado, P. L. O. A., Fidalgo, E. C. C., Coelho, M. R., and Madari, B. E.: Pedotransfer functions for estimating soil bulk density from existing soil survey reports in Brazil, Geoderma, 139, 90–97, https://doi.org/10.1016/j.geoderma.2007.01.005, 2007.
Bondi, G., Creamer, R., Ferrari, A., Fenton, O., and Wall, D.: Using machine learning to predict soil bulk density on the basis of visual parameters: Tools for in-field and post-field evaluation, Geoderma, 318, 137–147, https://doi.org/10.1016/j.geoderma.2017.11.035, 2018.
Chen, S., Richer-de-Forges, A. C., Saby, N. P. A., Martin, M. P., Walter, C., and Arrouays, D.: Building a pedotransfer function for soil bulk density on regional dataset and testing its validity over a larger area, Geoderma, 312, 52–63, https://doi.org/10.1016/j.geoderma.2017.10.009, 2018.
Chen, S., Xu, H., Xu, D., Ji, W., Li, S., Yang, M., Hu, B., Zhou, Y., Wang, N., Arrouays, D., and Shi, Z.: Evaluating validation strategies on the performance of soil property prediction from regional to continental spectral data, Geoderma, 400, 115159, https://doi.org/10.1016/j.geoderma.2021.115159, 2021.
Chen, S., Arrouays, D., Mulder, V. L., Poggio, L., Minasny, B., Roudier, P., Libohova, Z., Lagacherie, P., Shi, Z., Hannam, J., Meersmans, J., Richer-de-Forges, A. C., and Walter, C.: Digital mapping of GlobalSoilMap soil properties at a broad scale: A review, Geoderma, 409, 115567, https://doi.org/10.1016/j.geoderma.2021.115567, 2022.
Chen, S., Chen, Z., Zhang, X., Luo, Z., Schillaci, C., Arrouays, D., Richer-de-Forges, A. C., and Shi, Z.: European soil bulk density and organic carbon stock database using LUCAS Soil 2018 [Data set], Zenodo, https://doi.org/10.5281/zenodo.10211884, 2023.
Chen, Z., Shuai, Q., Shi, Z., Arrouays, D., Richer-de-Forges, A. C., and Chen, S.: National-scale mapping of soil organic carbon stock in France: New insights and lessons learned by direct and indirect approaches, Soil Environ. Health, 1, 100049, https://doi.org/10.1016/j.seh.2023.100049, 2023.
Cotrufo, M. F., Ranalli, M. G., Haddix, M. L., Six, J., and Lugato, E.: Soil carbon storage informed by particulate and mineral-associated organic matter, Nat. Geosci., 12, 989–994, https://doi.org/10.1038/s41561-019-0484-6, 2019.
Dam, R. F., Mehdi, B. B., Burgess, M. S. E., Madramootoo, C. A., Mehuys, G. R., and Callum, I. R.: Soil bulk density and crop yield under eleven consecutive years of corn with different tillage and residue practices in a sandy loam soil in central Canada, Soil Till. Res., 84, 41–53, https://doi.org/10.1016/j.still.2004.08.006, 2005.
Dawson, J. J. C. and Smith, P.: Carbon losses from soil and its consequences for land-use management, Sci. Total Environ., 382, 165–190, https://doi.org/10.1016/j.scitotenv.2007.03.023, 2007.
De Rosa, D., Ballabio, C., Lugato, E., Fasiolo, M., Jones, A., and Panagos, P.: Soil organic carbon stocks in European croplands and grasslands: How much have we lost in the past decade?, Glob. Change Biol., 30, e16992, https://doi.org/10.1111/gcb.16992, 2023.
Elzhov, T. V., Mullen, K. M., Spiess, A. N., and Bolker, B.: minpack.lm: R Interface to the Levenberg–Marquardt Nonlinear Least-Squares Algorithm Found in MINPACK, Plus Support for Bounds, https://cran.r-project.org/web/packages/minpack.lm/index.html (last access: 15 August 2023), 2015.
European Commission: LUCAS 2009 TOPSOIL data, European Commission [data set], https://esdac.jrc.ec.europa.eu/content/lucas-2009-topsoil-data (last access: 1 June 2023), 2013.
European Commission: LUCAS 2015 TOPSOIL data, European Commission [data set], https://esdac.jrc.ec.europa.eu/content/lucas2015-topsoil-data (last access: 1 June 2023), 2020.
European Commission: LUCAS 2018 TOPSOIL data, European Commission [data set], https://esdac.jrc.ec.europa.eu/content/lucas-2018-topsoil-data (last access: 1 June 2023), 2022.
Farr, T. G., Rosen, P. A., Caro, E., Crippen, R., Duren, R., Hensley, S., Kobrick, M., Paller, M., Rodriguez, E., Roth, L., Seal, D., Shaffer, S., Shimada, J., Umland, J., Werner, M., Oskin, M., Burbank, D., and Alsdorf, D.: The shuttle radar topography mission, Rev. Geophys., 45, RG2004, https://doi.org/10.1029/2005RG000183, 2007.
Fernández-Ugalde O., Orgiazzi A., Jones A., Lugato E., Panagos P.: LUCAS 2018 – SOIL COMPONENT: Sampling Instructions for Surveyors, JRC technical report, EUR 28501 EN, European Commission, Joint Research Centre, Ispra, Italy, https://doi.org/10.2760/023673, 2017.
Fernández-Ugalde, O., Orgiazzi, A., Marechal, A., Jones, A., Scarpa, S., Panagos, P., and Van Liedekerke, M.: LUCAS 2018 soil module: presentation of dataset and results, Publications Office of the European Union, Luxembourg, https://doi.org/10.2760/215013, 2022.
Fick, S. E. and Hijmans, R. J.: WorldClim 2: new 1-km spatial resolution climate surfaces for global land areas, Int. J. Climatol., 37, 4302–4315, https://doi.org/10.1002/joc.5086, 2017.
Ghehi, N. G., Nemes, A., Verdoodt, A., Van Ranst, E., Cornelis, W. M., and Boeckx, P.: Nonparametric techniques for predicting soil bulk density of tropical rainforest topsoils in Rwanda, Soil Sci. Soc. Am. J., 76, 1172–1183, https://doi.org/10.2136/sssaj2011.0330, 2012.
Gupta, A., Vasava, H. B., Das, B. S., and Choubey, A. K.: Local modeling approaches for estimating soil properties in selected Indian soils using diffuse reflectance data over visible to near-infrared region, Geoderma, 325, 59–71, https://doi.org/10.1016/j.geoderma.2018.03.025, 2018.
Gupta, S. C. and Larson, W. E.: Estimating soil-waster retention characteristics from particle-size distribution, organic-matter percent, and bulk-density, Water Resour. Res., 15, 1633–1635, https://doi.org/10.1029/WR015i006p01633, 1979.
Hollis, J. M., Hannam, J., and Bellamy, P. H.: Empirically-derived pedotransfer functions for predicting bulk density in European soils, Eur. J. Soil Sci., 63, 96–109, https://doi.org/10.1111/j.1365-2389.2011.01412.x, 2012.
Hu, B., Xie, M., Shi, Z., Li, H., Chen, S., Wang, Z., Zhou, Y., Ni, H., Geng, Y., Zhu, Q., and Zhang, X.: Fine-resolution mapping of cropland topsoil pH of Southern China and its environmental application, Geoderma, 442, 116798, https://doi.org/10.1016/j.geoderma.2024.116798, 2024.
Jalabert, S. S. M., Martin, M. P., Renaud, J. P., Boulonne, L., Jolivet, C., Montanarella, L., and Arrouays, D.: Estimating forest soil bulk density using boosted regression modelling, Soil Use Manage., 26, 516–528, https://doi.org/10.1111/j.1475-2743.2010.00305.x, 2010.
Katuwal, S., Knadel, M., Norgaard, T., Moldrup, P., Greve, M. H., and de Jonge, L. W.: Predicting the dry bulk density of soils across Denmark: Comparison of single-parameter, multi-parameter, and vis-NIR based models, Geoderma, 361, 114080, https://doi.org/10.1016/j.geoderma.2019.114080, 2020.
Lal, R.: Digging deeper: A holistic perspective of factors affecting soil organic carbon sequestration in agroecosystems, Glob. Change Biol., 24, 3285–3301, https://doi.org/10.1111/gcb.14054, 2018.
Lark, R. M., Rawlins, B. G., Robinson, D. A., Lebron, I., and Tye, A. M.: Implications of short-range spatial variation of soil bulk density for adequate field-sampling protocols: methodology and results from two contrasting soils, Eur. J. Soil Sci., 65, 803–814, https://doi.org/10.1111/ejss.12178, 2014.
Lemercier, B., Lagacherie, P., Amelin, J., Sauter, J., Pichelin, P., Richer-de-Forges, A. C., and Arrouays, D.: Multiscale evaluations of global, national and regional digital soil mapping products in France, Geoderma, 425, 116052, https://doi.org/10.1016/j.geoderma.2022.116052, 2022.
Li, S., Li, Q., Wang, C., Li, B., Gao, X., Li, Y., and Wu, D.: Spatial variability of soil bulk density and its controlling factors in an agricultural intensive area of Chengdu Plain, Southwest China, J. Integr. Agr., 18, 290–300, https://doi.org/10.1016/S2095-3119(18)61930-6, 2019.
Liu, Y., Chen, S., Yu, Q., Cai, Z., Zhou, Q., Bellingrath-Kimura, S. D., and Wu, W.: Improving digital mapping of soil organic matter in cropland by incorporating crop rotation, Geoderma, 438, 116620, https://doi.org/10.1016/j.geoderma.2023.116620, 2023.
Maestre, F. T., Benito, B. M., Berdugo, M., Concostrina-Zubiri, L., Delgado-Baquerizo, M., Eldridge, D. J., Guirado, E., Gross, N., Kéfi, S., Bagousse-Pinguet, Y. L., Ochoa-Hueso, R., and Soliveres, S.: Biogeography of global drylands, New Phytol., 231, 540–558, https://doi.org/10.1111/nph.17395, 2021.
Makovníková, J., Širáň, M., Houšková, B., Pálka, B., and Jones, A.: Comparison of different models for predicting soil bulk density. Case study–Slovakian agricultural soils, Int. Agrophys., 31, 491–498, https://doi.org/10.1515/intag-2016-0079, 2017.
Meyer, H. and Pebesma, E.: Predicting into unknown space? Estimating the area of applicability of spatial prediction models, Methods Ecol. Evol., 12, 1620–1633, https://doi.org/10.1111/2041-210X.13650, 2021.
Munera-Echeverri, J.-L., Martin, M. P., Boulonne, L., Saby, N. P. A., and Arrouays, D.: Assessing carbon stock changes in French top soils in croplands and grasslands: comparison of fixed depth and equivalent soil mass. 22th World Congress of Soil Sciences, Jul 2022, Glasgow, United Kingdom, https://doi.org/10.1111/ejss.12002, 2022.
Nasta, P., Palladino, M., Sica, B., Pizzolante, A., Trifuoggi, M., Toscanesi, M., Giarra, A., D'Auria, J., Nicodemo, F., Mazzitelli, C., Lazzaro, U., Fiore, D. P., and Romano, N.: Evaluating pedotransfer functions for predicting soil bulk density using hierarchical mapping information in Campania, Italy, Geoderma Reg., 21, e00267, https://doi.org/10.1016/j.geodrs.2020.e00267, 2020.
Nocita, M., Stevens, A., Toth, G., Panagos, P., van Wesemael, B., and Montanarella, L.: Prediction of soil organic carbon content by diffuse reflectance spectroscopy using a local partial least square regression approach, Soil Biol. Biochem., 68, 337–347, https://doi.org/10.1016/j.soilbio.2013.10.022, 2014.
Orgiazzi, A., Panagos, P., Fernández-Ugalde, O., Wojda, P., Labouyrie, M., Ballabio, C., Franco, A., Pistocchi, A., Montanarella, L and Jones, A.: LUCAS Soil Biodiversity and LUCAS Soil Pesticides, new tools for research and policy development, Eur. J. Soil Sci., 73, e13299, https://doi.org/10.1111/ejss.13299, 2022.
Pacini, L., Yunta, F., Jones, A., Montanarella, L., Barrè, P., Saia, S., Chen, S., and Schillaci, C.: Fine earth soil bulk density at 0.2 m depth from Land Use and Coverage Area Frame Survey (LUCAS) soil 2018, Eur. J. Soil Sci., 74, e13391, https://doi.org/10.1111/ejss.13391, 2023.
Padarian, J., Minasny, B., and McBratney, A. B.: Transfer learning to localise a continental soil vis-NIR calibration model, Geoderma, 340, 279–288, https://doi.org/10.1016/j.geoderma.2019.01.009, 2019.
Palladino, M., Romano, N., Pasolli, E., and Nasta, P.: Developing pedotransfer functions for predicting soil bulk density in Campania, Geoderma, 412, 115726, https://doi.org/10.1016/j.geoderma.2022.115726, 2022.
Palmtag, J., Obu, J., Kuhry, P., Richter, A., Siewert, M. B., Weiss, N., Westermann, S., and Hugelius, G.: A high spatial resolution soil carbon and nitrogen dataset for the northern permafrost region based on circumpolar land cover upscaling, Earth Syst. Sci. Data, 14, 4095–4110, https://doi.org/10.5194/essd-14-4095-2022, 2022.
Panagos, P., Van Liedekerke, M., Borrelli, P., Köninger, J., Ballabio, C., Orgiazzi, A., Lugato, E., Liakos, L., Hervas, J., Jones, A and Montanarella, L.: European Soil Data Centre 2.0: Soil data and knowledge in support of the EU policies, Eur. J. Soil Sci., 73, e13315, https://doi.org/10.1111/ejss.13315, 2022.
Panagos, P., De Rosa, D., Liakos, L., Labouyrie, M., Borrelli, P., and Ballabio, C.: Soil bulk density assessment in Europe, Agr. Ecosyst. Environ., 364, 108907, https://doi.org/10.1016/j.agee.2024.108907, 2024.
Patton, N. R., Lohse, K. A., Seyfried, M., Will, R., and Benner, S. G.: Lithology and coarse fraction adjusted bulk density estimates for determining total organic carbon stocks in dryland soils, Geoderma, 337, 844–852, https://doi.org/10.1016/j.geoderma.2018.10.036, 2019.
Perie, C. and Ouimet, R.: Organic carbon, organic matter and bulk density relationships in boreal forest soils, Can. J. Soil Sci., 88, 315–325, https://doi.org/10.4141/cjss06008, 2008.
Poeplau, C., Vos, C., and Don, A.: Soil organic carbon stocks are systematically overestimated by misuse of the parameters bulk density and rock fragment content, SOIL, 3, 61–66, https://doi.org/10.5194/soil-3-61-2017, 2017.
Pribyl, D. W.: A critical review of the conventional SOC to SOM conversion factor, Geoderma, 156, 75–83, https://doi.org/10.1016/j.geoderma.2010.02.003, 2010.
Rabot, E., Wiesmeier, M., Schlüter, S., and Vogel, H. J.: Soil structure as an indicator of soil functions: A review, Geoderma, 314, 122–137, https://doi.org/10.1016/j.geoderma.2017.11.009, 2018.
Ramcharan, A., Hengl, T., Beaudette, D., and Wills, S.: A soil bulk density pedotransfer function based on machine learning: A case study with the ncss soil characterization database, Soil Sci. Soc. Am. J., 81, 1279–1287, https://doi.org/10.2136/sssaj2016.12.0421, 2017.
Rawls, W. J. and Brakensiek, D. L.: Prediction of soil water properties for hydrologic modeling, ASCE, in: Proceedings of a Symposium Watershed Management in the Eighties, New York, 30 April–1 May 1985, edited by: Jones, E. B. and Ward, T. J., 293–299, 1985.
Richer-de-Forges, A. C., Arrouays, D., Poggio, L., Chen, S., Lacoste, M., and Minasny, B.: Hand-feel soil texture observations to evaluate the accuracy of digital soil maps for local prediction of particle size distribution. A case study in central France, Pedosphere, 33, 731–743, https://doi.org/10.1016/j.pedsph.2022.07.009, 2023.
Sanderman, J., Savage, K., and Dangal, S. R.: Mid-infrared spectroscopy for prediction of soil health indicators in the United States, Soil Sci. Soc. Am. J., 84, 251–261, https://doi.org/10.1002/saj2.20009, 2020.
Schillaci, C., Perego, A., Valkama, E., Märker, M., Saia, S., Veronesi, F., Lipani, A., Lombardo, L., Tadiello, T., Gamper, G. A., Tedone, L., Moss, C., Pareja-Serrano, E., Amato, G., Kühl, K., Dămătîrcă, C., Cogato, A., Mzid, N., Eeswaran, R., Rabelo, M., Sperandio, G., Bosino, A., Bufalini, M., Tunçay, T., Ding, J., Fiorentini, M., Tiscornia, G., Conradt, S., Botta, M., and Acutis, M.: New pedotransfer approaches to predict soil bulk density using WoSIS soil data and environmental covariates in Mediterranean agro-ecosystems, Sci. Total Environ., 780, 146609, https://doi.org/10.1016/j.scitotenv.2021.146609, 2021.
Schrumpf, M., Schulze, E. D., Kaiser, K., and Schumacher, J.: How accurately can soil organic carbon stocks and stock changes be quantified by soil inventories?, Biogeosciences, 8, 1193–1212, https://doi.org/10.5194/bg-8-1193-2011, 2011.
Shiri, J., Keshavarzi, A., Kisi, O., Karimi, S., and Iturraran-Viveros, U.: Modeling soil bulk density through a complete data scanning procedure: Heuristic alternatives, J. Hydrol., 549, 592–602, https://doi.org/10.1016/j.jhydrol.2017.04.035, 2017.
Sprengel, C.: Ueber Pflanzenhumus, Humussaüre und humussaure Salze, Archiv für die Gesammte Naturlehre, 8, 145–220, 1826.
Sun, W., Canadell, J. G., Yu, L., Yu, L., Zhang, W., Smith, P., Fischer, T., and Huang, Y.: Climate drives global soil carbon sequestration and crop yield changes under conservation agriculture, Glob. Change Biol., 26, 3325–3335, https://doi.org/10.1111/gcb.15001, 2020.
Taalab, K., Corstanje, R., Mayr, T. M., Whelan, M. J., and Creamer, R. E: The application of expert knowledge in Bayesian networks to predict soil bulk density at the landscape scale, Eur. J. Soil Sci., 66, 930–941, https://doi.org/10.1111/ejss.12282, 2015.
Tao, F., Huang, Y., Hungate, B. A., Manzoni, S., Frey, S. D., Schmidt, M. W. I., Reichstein, M., Carvalhais, N., Ciais, P., Jiang, L., Lehmann, J., Wang, Y., Houlton, B. Z., Ahrens, B., Mishra, U., Hugelius, G., Hocking, T. D., Lu, X., Shi, Z., Viatkin, K., Vargas, R., Yigini, Y., Omutom C., Malik, A. A., Peralta, G., Cuevas-Corona, R., Paolo, L. E. D., Luotto, I., Liao, C., Liang, Y., Saynes, V. S., Huang, X., and Luo, Y.: Microbial carbon use efficiency promotes global soil carbon storage, Nature, 618, 981–985, https://doi.org/10.1038/s41586-023-06042-3, 2023.
Tautges, N. E., Chiartas, J. L., Gaudin, A. C., O'Geen, A. T., Herrera, I., and Scow, K. M.: Deep soil inventories reveal that impacts of cover crops and compost on soil carbon sequestration differ in surface and subsurface soils, Glob. Change Biol., 25, 3753–3766, https://doi.org/10.1111/gcb.14762, 2019.
Tifafi, M., Guenet, B., and Hatté, C.: Large Differences in Global and Regional Total Soil Carbon Stock Estimates Based on SoilGrids, HWSD, and NCSCD: Intercomparison and Evaluation Based on Field Data From USA, England, Wales, and France: Differences in total SOC stock estimates, Global Biogeochem. Cy., 32, 42–56, https://doi.org/10.1002/2017GB005678, 2018.
Van Bemmelen, J. M.: Über die Bestimmung des Wassers, des Humus, des Schwefels, der in den colloïdalen Silikaten gebundenen Kieselsäure, des Mangans u.s.w. im Ackerboden, Die Landwirthschaftlichen Versuchs-Stationen, 37, 279–290, 1890.
Van Looy, K., Bouma, J., Herbst, M., Koestel, J., Minasny, B., Mishra, U., Montzka, C., Nemes, A., Pachepsky, Y. A., Padarian, J., Schaap, M. G., Tóth, B., Verhoef, A., Vanderborght, J., van der Ploeg, M. J., Weihermüller, L., Zacharias, S., Zhang, Y., and Vereecken, H.: Pedotransfer functions in Earth system science: Challenges and perspectives, Rev. Geophys., 55, 1199–1256, https://doi.org/10.1002/2017RG000581, 2017.
Wang, M., Guo, X., Zhang, S., Xiao, L., Mishra, U., Yang, Y., Zhu, B., Wang, G., Mao, X., Qian, T., Jiang, T., Shi, Z., and Luo, Z.: Global soil profiles indicate depth-dependent soil carbon losses under a warmer climate, Nat. Commun., 13, 5514, https://doi.org/10.1038/s41467-022-33278-w, 2022.
Wang, N., Chen, S., Huang, J., Frappart, F., Taghizadeh, R., Zhang, X., Wigneron, J. P., Xue, J., Xiao, Y., Peng, J., and Shi, Z.: Global Soil Salinity Estimation at 10 m Using Multi-source Remote Sensing, J. Remote Sens., https://doi.org/10.34133/remotesensing.0130, 2024.
Wang, Y., Luo, G., Li, C., Ye, H., Shi, H., Fan, B., Zhang, W., Zhang, C., Xie, M., and Zhang, Y.: Effects of land clearing for agriculture on soil organic carbon stocks in drylands: A meta-analysis, Glob. Change Biol., 29, 547–562, https://doi.org/10.1111/gcb.16481, 2023.
Wendt, J. W. and Hauser, S.: An equivalent soil mass procedure for monitoring soil organic carbon in multiple soil layers, Eur. J. Soil Sci., 64, 58–65, https://doi.org/10.1111/ejss.12002, 2013.
Wiesmeier, M., Spörlein, P., Geuß, U., Hangen, E., Haug, S., Reischl, A., Schilling, B., von Lützow, M., and Kögel-Knabner, I.: Soil organic carbon stocks in southeast Germany (Bavaria) as affected by land use, soil type and sampling depth, Glob. Change Biol., 18, 2233–2245, https://doi.org/10.1111/j.1365-2486.2012.02699.x, 2012.
Xiao, Y., Xue, J., Zhang, X., Wang, N., Hong, Y., Jiang, Y., Zhou, Y., Teng, H., Hu, B., Lugato, E., Richer-de-Forges, A. C., Arrouays, D., Shi, Z., and Chen, S.: Improving pedotransfer functions for predicting soil mineral associated organic carbon by ensemble machine learning, Geoderma, 428, 116208, https://doi.org/10.1016/j.geoderma.2022.116208, 2022a.
Xiao, Y., Xue, J., Zhang, X., Wang, N., Hong, Y., Jiang, Y., Zhou, Y., Teng, H., Hu, B., Lugato, E., Richer-de-Forges, A.C., Arrouays, D., Shi, Z., and Chen, S.: Forward Recursive Feature Selection, Zenodo [software], https://doi.org/10.5281/zenodo.7141020, 2022b.
Yi, X., Li, G., and Yin, Y.: Pedotransfer functions for estimating soil bulk density: A case study in the three-river headwater region of Qinghai Province, China, Pedosphere, 26, 362–373, https://doi.org/10.1016/S1002-0160(15)60049-2, 2016.
Yost, J. L. and Hartemink, A. E.: How deep is the soil studied–an analysis of four soil science journals, Plant Soil, 452, 5–18, https://doi.org/10.1007/s11104-020-04550-z, 2020.
Zhang, X., Chen, S., Xue, J., Wang, N., Xiao, Y., Chen, Q., Hong, Y., Zhou, Y., Teng, H., Hu, B., Zhuo, Z., Ji, W., Huang, Y., Gou, Y., Richer-de-Forges, A. C., Arrouays, D., and Shi, Z.: Improving model parsimony and accuracy by modified greedy feature selection in digital soil mapping, Geoderma, 432, 116383, https://doi.org/10.1016/j.geoderma.2023.116383, 2023.
Zhu, C., Byrd, R. H., Lu, P., and Nocedal, J.: Algorithm 778: L-BFGS-B: Fortran subroutines for large-scale bound-constrained optimization, ACM T. Math. Software, 23, 550–560, https://doi.org/10.1145/279232.279236, 1997.
Zomer, R. J., Xu, J., and Trabucco, A.: Version 3 of the global aridity index and potential evapotranspiration database, Sci. Data, 9, 409–409, https://doi.org/10.1038/s41597-022-01493-1, 2022.