Enriching the GEOFON seismic catalog with automatic energy magnitude estimations

We present a seismic catalog (Bindi et al., 2024, https://doi.org/10.5880/GFZ.2.6.2023.010) including energy magnitude M_e estimated from P waves recorded at teleseismic distances in the range $\mathrm{20}\mathit{°}\le \mathrm{\Delta }\le \mathrm{98}\mathit{°}$ and for depths shorter than 80 km. The catalog is built starting from the event catalog disseminated by GEOFON (GEOFOrschungsNetz), considering 6349 earthquakes with moment magnitude M_w≥5 occurring between 2011 and 2023. Magnitudes are computed using 1 031 396 freely available waveforms archived in EIDA (European Integrated Data Archive) and IRIS (Incorporated Research Institutions for Seismology) repositories, retrieved through the standard International Federation of Digital Seismograph Networks (FDSN) web services (https://www.fdsn.org/webservices/, last access: March 2024). A reduced, high-quality catalog for events with M_w≥5.8 and from which stations and events with only few recordings were removed forms the basis of a detailed analysis of the residuals of individual station measurements, which are decomposed into station- and event-specific terms and a term accounting for remaining variability. The derived M_e values are compared to M_w computed by GEOFON and with the M_e values calculated by IRIS. Software and tools developed for downloading and processing waveforms for bulk analysis and an add-on for SeisComP for real-time assessment of M_e in a monitoring context are also provided alongside the catalog. The SeisComP add-on has been part of the GEOFON routine processing since December 2021 to compute and disseminate M_e for major events via the existing services.

1 Introduction

Several magnitude scales have been defined to characterize the size of an earthquake. We can, however, divide magnitude scales in two groups, with one including magnitudes based on the amplitudes and periods of different seismic phases measured on band-limited signals (e.g., the body and surface wave magnitudes; Gutenberg, 1945a, b) and the other including magnitude scales related to estimations of macroscopic physical parameters of the earthquake source. The latter comprise the moment (M_w; Kanamori, 1977; Hanks and Kanamori, 1979) and the energy (M_e; Boatwright and Choy, 1986) magnitudes, which are based on seismic moment (Aki, 1966) and radiated seismic energy (Haskell, 1964), respectively. These two magnitude scales are somewhat complementary because, although both represent an estimation of earthquake-related energy, they are determined by different parts of the source spectrum. The seismic moment extrapolated from the low-frequency end and represents the release of elastic energy stored in the Earth's crust or mantle being proportional to the integrated slip across the fault surface. The radiated seismic energy describes the fraction of the total energy released being radiated as seismic waves across all frequencies; i.e., it depends on the earthquake dynamics such as rupture velocity but also stress drop. M_e estimates have been shown to play an important role when used in conjunction with M_w to better characterize the tsunami and shaking potential of an earthquake (Newman and Okal, 1998; Di Giacomo et al., 2010).

M_w is routinely computed from long period signals of broadband recordings, and it has become a robust and reliable source parameter for large and moderate earthquakes worldwide (Di Giacomo et al., 2021). On the other hand, the computation of M_e is hindered by the necessity of integrating the velocity power spectra over a wide frequency range, while using signals in a limited bandwidth and taking into account propagation effects at high frequencies.

Aiming at validating and testing the procedures for operational purposes, we present a seismic catalog of M_e computed, following the methodology proposed by Di Giacomo et al. (2008) and Di Giacomo et al. (2010) for the rapid assessment of energy magnitude (i.e., without requiring additional source information other than the hypocentral location). The approach is based on the analysis of spectra computed for teleseismic vertical component P waveforms. Teleseismic P waves are commonly used to compute M_e for global earthquakes, as their energy loss during propagation can be more reliably modeled compared to S waves. We further present a detailed analysis of the residuals in a reduced high-quality catalog for events with M_w≥5.8 with respect to the M_w available in the GEOFON (GEOFOrschungsNetz) catalog and the M_e values computed by IRIS.

2 Energy magnitude computation

2.1 Single-station estimation

We implement the methodology proposed by Di Giacomo et al. (2008) and Di Giacomo et al. (2010) to compute M_e. Teleseismic vertical component P waveforms (BHZ channels, where B stands for broadband, H for high-gain seismometer, and Z for vertical component) are analyzed in the distance range from 20° to 98° and for earthquakes shallower than 80 km. Standard teleseismic range usually starts at 30°, but we use 20° to allow closer stations to be used for rapid response purposes. Shorter distances, however, are difficult to include for global earthquakes, as regional effects are not well accounted for with a 1-D model. Propagation effects are accounted for by frequency-dependent amplitude decay functions that are computed numerically (Wang, 1999) for the ak135Q model (Kennett et al., 1995; Montagner and Kennett, 1996) in the frequency range 0.012–1 Hz.

An estimate of radiated seismic energy E_s is obtained for each single station from the integral of the power spectra of the vertical component P waveform, which is corrected for propagation effects (Haskell, 1964):

$$\begin{array}{}\text{(1)}& E_{\mathrm{s}}=\left[{\displaystyle \frac{\mathrm{2}}{\mathrm{15}\mathit{\pi }\mathit{\rho }{\mathit{\alpha }}^{\mathrm{5}}}}+{\displaystyle \frac{\mathrm{1}}{\mathrm{5}\mathit{\pi }\mathit{\rho }{\mathit{\beta }}^{\mathrm{5}}}}\right]\underset{f_{\mathrm{1}}}{\overset{f_{\mathrm{2}}}{\int }}{\left|{\displaystyle \frac{\dot{u}\left(f\right)}{G\left(f\right)/\mathrm{2}\mathit{\pi }f}}\right|}^{\mathrm{2}}\mathrm{d}f,\end{array}$$

where α, β, and ρ are the P-wave velocity, S-wave velocity, and the density at the source, respectively. f is the frequency, and f₁=0.012 Hz and f₂=1 Hz are the lower and upper limits of the considered spectral bandwidth. $\dot{u}\left(f\right)$ is the P-wave velocity spectrum. G(f) is the median value of Green's function spectrum for displacement, computed from multiple combinations of focal mechanisms and varying strike, dip, and rake over a regular grid (Di Giacomo et al., 2008).

We used analysis windows starting 10 s before the P arrival and with lengths of 90 s for M_w≤7.5, 120 s for $\mathrm{7.5}<M_{\mathrm{w}}\le \mathrm{8.5}$, and 180 s for M_w>8.5. The energy magnitude M_e estimate for a single-event station pair is in turn computed as $M_{\mathrm{e}}=\mathrm{2}/\mathrm{3}({\log }_{\mathrm{10}}{E}_{\mathrm{s}}-\mathrm{4.4})$, with E_s given in joules (Bormann et al., 2002). The procedure provides M_e estimates at each recording station that can be averaged to minimize path-specific deviations not accounted for by the theoretical model (e.g., directivity and focal mechanism effects and regional variations in attenuation).

2.2 Open-source tool for computing M_e

The above procedure is implemented in the package me-compute (Zaccarelli, 2023). The program uses stream2segment (Zaccarelli et al., 2019; Zaccarelli, 2018) to download events, station metadata, and waveforms from International Federation of Digital Seismograph Networks (FDSN)-compliant repositories in a structured query language (SQL) database.

In our application, the download is configured to fetch events from the GEOFON (Quinteros et al., 2021) event web service, selecting events with computed M_w in the time span 2011–2023. Waveforms are download from EIDA (Strollo et al., 2021) and IRIS (https://service.iris.edu/, last access: March 2024) data centers. The processing routine is implemented in a Python module, which computes the station energy magnitude for each downloaded waveform segment, as summarized in Sect. 2.1, and then calculates the event energy magnitude M_e as the mean of all station magnitudes within the 5th–95th percentile range.

The final output consists of the following files:

• a tabular file in a hierarchical data format (HDF), where each row represents the metadata and measurements, specifically also the station energy magnitude estimate, for a single waveform;

• a tabular file in a comma-separated value (CSV) format aggregating the results of the previous file, where each row represents a seismic event, reporting the event data end metadata and including the M_e estimate for the event;

• an HTML (HyperText Markup Language) file visualizing the selected content reported in the CSV file, where the information for each event can be visualized on an interactive map; and

• one file per processed event in the Quake Markup Language (QuakeML) format, where we also included the M_e value.

All files produced by me-compute are disseminated in the data archive (Bindi et al., 2024; https://doi.org/10.5880/GFZ.2.6.2023.010), along with the stream2segment and me-compute configuration files.

3 Catalog compilation

We use me-compute to compute M_e for M_w≥5 earthquakes since 2011 in the GEOFON catalog. Table 1 summarizes the steps followed to compile the disseminated M_e catalog. The catalog reports the single-waveform energy magnitude M_eij estimated at station j for earthquake i. The energy magnitude M_e for each considered event i is then computed as the median of M_eij over the set of recording stations, without considering station static corrections. The starting dataset D0 consists of more than 1 000 000 waveforms (channels BHZ) generated by 6963 earthquakes recorded by 7765 stations belonging to 246 different networks. Only recordings with an average signal-to-noise ratio (SNR) for the amplitude greater than 3 within the frequency range of interest are included in D0. Several integrity and quality checks are applied to remove outliers and faulty signals. Dataset D1 is obtained by analyzing the median residual at the network level, discarding 14 networks characterized by median residuals outside the 2.5 and 97.5 percentile range (Fig. 1a). Dataset D2 is then generated by analyzing the station median values and excluding 382 stations with residuals outside the 2.5–97.5 percentile range (Fig. 1b). Most of the networks and stations removed will have instrumental problems or faulty metadata regarding instrument responses, although in some cases stations with very strong site effects might also be excluded.

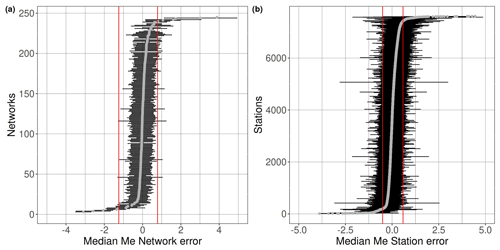
Figure 1 Median network residuals (circles) for dataset D0 (a) and median station residuals for dataset D1 (b). Red lines correspond to the 2.5 and 97.5 percentiles of the distributions. For each network (a) and station (b), the horizontal bars correspond to the interval median (circle) ±1 median absolute deviation (MAD). A few values falling outside the range considered for the horizontal axis are not shown.

An anomaly score is computed to further refine the dataset by flagging anomalous amplitudes using the software sdaas (Zaccarelli, 2022). The software, developed from the work of Zaccarelli et al. (2021), is based on a machine learning algorithm specifically designed for outlier detection (Isolation Forest) which computes an anomaly score in [0,1], representing the degree of belief of a waveform to be an outlier. The score can be used to assign robustness weights or to define thresholds above which data can be discarded. After inspecting the distribution of the anomaly scores, we set the threshold to 0.62 for M_w<7.5 and to 0.80 for M_w≥7.5.

The spatial distribution of events and stations generating dataset D3 (Bindi et al., 2024) are shown in Fig. 2a, b. The corresponding M_e residuals are shown in Fig. 3 against distance and M_w. The largest positive residuals correspond mostly to earthquakes with M_w<6 recorded at distances Δ>60°, where the implemented methodology is expected to generate biased station M_e estimates due to the limitations in the analyzed bandwidth and low signal-to-noise ratio (Di Giacomo et al., 2008, 2010). The overall residual distribution is unbiased and does not show trends of the mean value with distance and magnitude.

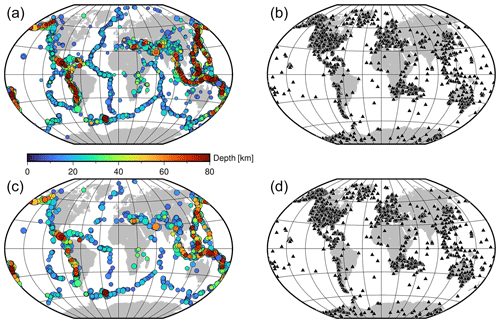
Figure 2 Panels (a) and (b) show event and station locations for dataset D3 (Table 1), respectively. Panels (c) and (d) show event and station locations for dataset D6 (Table 1), respectively.

Table 1 Datasets considered in this study. Datasets in bold are available in Bindi et al. (2024).

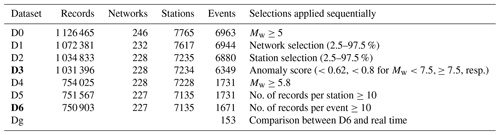
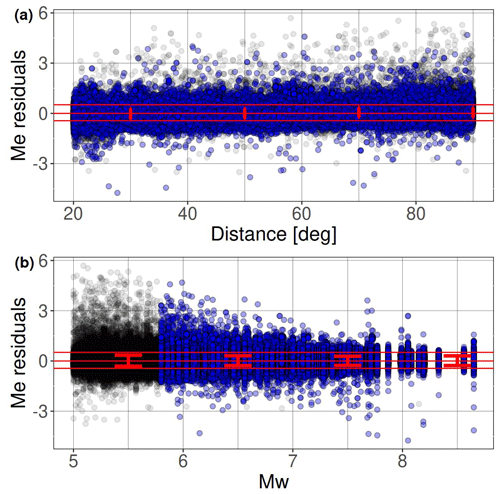
Figure 3 Energy magnitude residuals versus distance (a) and moment magnitude (b) for dataset D3. Blue dots indicate residuals also included in D6. The horizontal red lines bound the 90 % confidence interval $[-\mathrm{0.43},\mathrm{0.50}]$ of the residual distribution. The error bars indicate the mean ±1 standard deviation of the residuals computed over different distance (20° wide) and magnitude (1 m.u. wide) intervals.

Therefore, we further limit the dataset by only considering events with M_w≥5.8 and at least 10 single-station measurements; we further exclude stations with fewer than 10 recordings in total. We added a column in the disseminated D3 dataset to flag lines corresponding to D6. It consists of ∼750 000 waveforms for 1671 earthquakes and 7135 stations. The event and station locations of D6 are shown in Fig. 2c and d.

4 Quality assessment via residual analysis

We perform residual analysis to validate the D6 catalog. The relationship between M_e and M_w is analyzed by performing the following mixed-effects regression (Bates et al., 2015; Stafford, 2014):

$$\begin{array}{}\text{(2)}& M_{\mathrm{e}ij}=c_{\mathrm{1}}+c_{\mathrm{2}}{M}_{\mathrm{w}i}+\mathit{\delta }{S}_j+\mathit{\delta }{E}_i+{\mathit{ϵ}}_{ij},\end{array}$$

where M_eij is the single-waveform energy magnitude estimate at station j for earthquake i, M_wi is the moment magnitude of earthquake i, intercept c₁ and slope c₂ parameters define the median model, and δS_i and δE_j are terms that capture station-specific and earthquake-specific adjustments, respectively. ϵ_ij accounts for the leftover effects (i.e., residuals that are specific to a particular path/waveform). The random effects δS, δE, and ϵ are zero mean normal distributions by construction. In particular, δS_j (inter-station residual) can represent site effects or instrumental gain corrections, with most of the latter probably removed by the outlier filtering stages described above. The interevent residual δE_i is an event-specific deviation from the M_e expected for a given M_w from the linear regression term. Finally, ϵ_ij can be thought of as a noise term for individual measurements, which can be either related to path-specific heterogeneity in attenuation with respect to the 1-D reference model or the influence of ambient noise on the actual measurement.

The interevent and inter-station term distributions are shown in Fig. 4, which are described by standard deviations of τ=0.246 and ϕ_S=0.188 m.u., respectively; the standard deviation of the ϵ is ϕ₀=0.232 m.u. When combining the interevent variability τ with the intra-event variability equal to $\mathit{\varphi }=\sqrt{{\mathit{\varphi }}_{\mathrm{0}}^{\mathrm{2}}+{\mathit{\varphi }}_{\mathrm{S}}^{\mathrm{2}}}$, we obtain the total standard deviation $\mathit{\sigma }=\sqrt{{\mathit{\tau }}^{\mathrm{2}}+{\mathit{\varphi }}^{\mathrm{2}}}=\mathrm{0.407}$, which represents the variability in the single-station M_eij residuals with respect to the average M_e computed per event. It is worth noting that the δS_j values can be used as station corrections to compute the energy magnitude of new events. In this case, the inter-station contribution to the total variability is removed, and the expected variability in the M_eij distribution is reduced to $\sqrt{{\mathit{\tau }}^{\mathrm{2}}+{\mathit{\varphi }}_{\mathrm{0}}^{\mathrm{2}}}=\mathrm{0.338}$. Finally, the linear regression model is defined by the coefficients $c_{\mathrm{1}}=(\mathrm{0.77}\pm \mathrm{0.09})$ m.u. and $c_{\mathrm{2}}=(\mathrm{0.92}\pm \mathrm{0.01})$. Considering the simplicity of the linear model in Eq. (2) and the large dataset analyzed, the uncertainty in the median model (sometimes referred to as σ_μ; Atik and Youngs, 2014) is very low, increasing from 0.007 for M_w=6 to 0.039 for M_w=9.

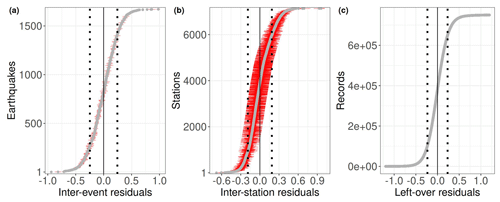
Figure 4 Cumulative distribution functions for event δE (a), station δS (b), and leftover ϵ distributions (circles) determined according to the mixed-effects regression in Eq. (2) applied to dataset D6. Dotted lines correspond to standard deviations ±1τ (a), ±1ϕ_S (b), and ±1ϕ₀ (c). Horizontal red lines in panels (a) and (b) are the standard errors in the random effects. In panel (c), values of ϵ exceeding ±1.2 in absolute value are not shown.

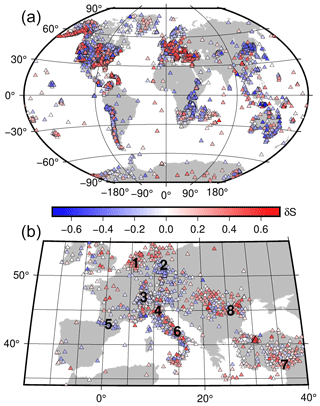
Figure 5 (a) Distribution of the site-specific residuals δS (see Eq. 2) and (b) magnified view over a portion of Europe. Numbers in panel (b) indicate the following locations: (1) Netherlands; (2) Harz highlands, Germany; (3) Switzerland; (4) Po plain, Italy; (5) Pyrenees mountain range; (6) Apennine Mountains; (7) East Anatolian Fault region; and (8) Moesian Platform.

We show the spatial distribution of δS in Fig. 5. Since M_eij is computed considering spectral values below 1 Hz and using teleseismic recordings for distances above 20°, δS capture station-specific effects connected to large-scale geological and tectonic crustal features, as exemplified in Fig. 5b for stations located in Europe. Positive δS (i.e., M_eij larger than the median) are observed for stations located in basins like in the Po plain, in the Moesian region, in the Netherlands, and in the East Anatolian Fault region. Negative values δS (i.e., M_eij lower than the median) are observed for stations located in mountain ranges such as the Pyrenees, the Alps, or in Harz Highlands and also tectonically highly active regions that are as cratonic as the East African Rift. The station terms can represent both site amplification, e.g., for stations in sedimentary basins, and anomalously high or low attenuation in the crust and or mantle surrounding the station. The station-specific residuals are disseminated along with the catalog to allow the computation of M_e for future earthquakes, while taking into account static magnitude corrections to reduce variability.

The spatial distribution of the interevent variability, δE, is shown in Fig. 6 for the smallest and largest values.

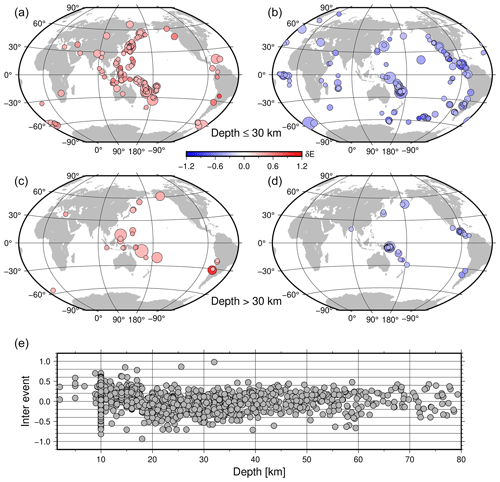
Figure 6 Extreme values for event specific residuals δE for the M_eij versus M_w mixed-effects model of Eq. (2). Only values below the 10th percentile (panels b and d) and above the 90th percentile (panels a and c) of the distribution are shown (the percentiles are about ±0.3). In panels (a) and (b), earthquakes with hypocentral depths shallower than 30 km are selected. In panels (c) and (d), events deeper than 30 km are considered. The distribution of δE versus depth for all events is shown in panel (e).

Considering depths shallower than 30 km (Fig. 6a and b), continental Asia, the Philippines, and Indonesia, as well as the Aleutian Islands, show positive values. California, Mexico, central America, and the Mid-Atlantic Ridge are characterized mostly by negative values. Considering deeper events (Fig. 6c and d), Japan and the Philippines have mostly positive values, while Mexico and central America have mostly negative values. The event-specific residuals are also disseminated, along with the catalog to increase the usefulness of the product from the event point of view, to allow the user to perform further refinements.

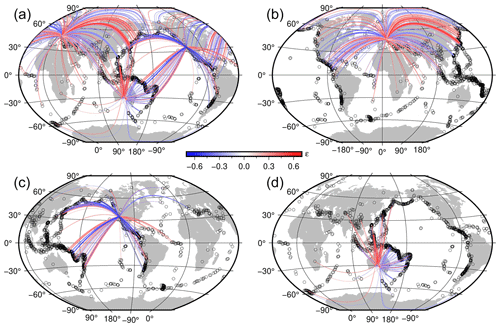
Figure 7 (a) Residual distribution ϵ of Eq. (2) for three different receiving areas, showing only $\left|\mathit{ϵ}\right|>\mathrm{0.30}$. (b) As in panel (a) but considering only the European receiving area. (c) As in panel (a) but considering only the receiving area in California. (d) As in panel (a) but considering only the receiving area in Australia. Circles indicate the earthquake locations.

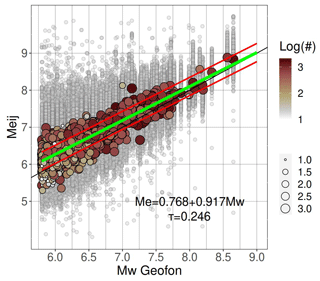
Figure 8 M_eij versus M_w scaling. Gray circles are the station M_eij estimates, and filled circles represent event M_e values calculated as medians of all station estimates for that event. Color indicates how many stations contributed to each estimate. The best-fit line in green is derived from the mixed-effects regression (Eq. 2), considering ±1 interevent standard deviation τ (red lines). The faint black line shows equality for reference.

Path-specific residuals ϵ are shown in Fig. 7 for three selected receiving areas in Europe, California, and Australia. Since in the partition of the residuals the leftover distribution ϵ represents the component not related to systematic station and event effects, they are mostly connected to lateral variability in attenuation in the Earth's interior with respect to the used global 1-D model and amplitude variation related to P-wave radiation patterns for different focal mechanisms.

Finally, the M_eij versus M_w scaling defined by the linear regression coefficients c₁ and c₂ of Eq. (2) is shown in Fig. 8.

4.1 Catalog validation: comparison with IRIS

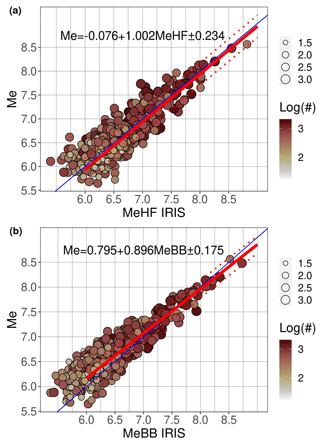
The energy magnitude computed in this study is compared to the values disseminated by IRIS through the SPUD service IRIS DMC (2013). The methodology implemented by IRIS is described by Convers and Newman (2011) and based on the analysis of Boatwright and Choy (1986) and Newman and Okal (1998). Similar to our approach, the energy flux is computed from the P-wave group (P + pP + sP) in the frequency domain. The single-station estimations are corrected for frequency-dependent anelastic attenuation effects and converted back to the energy radiated by the source by applying corrections for geometrical spreading, depth, and mechanism-dependent effects for P waves and considering a theoretical partition of the energy between P and S waves. The energy is computed considering the frequency range 0.014–2 Hz (broadband for M_e(BB)) or 0.5-02 Hz (high frequency for M_e(HF)), analyzing stations in the distance range 25–80°. The duration of the time window used for the computation is based on analysis of the cumulative high-frequency energy (0.5–2 Hz) as a function of time. The crossover time used to compute the energy flux is identified at the intersection between the near-constant increasing rate for short times and the relative flat asymptotic behavior for long durations. The SPUD service disseminates both the high-frequency M_e(HF) and broadband M_e(BB) estimates.

Two regression models are calibrated against the broadband and high-frequency estimates disseminated by IRIS through SPUD. The best-fit models, shown in Fig. 9, are $M_{\mathrm{e}}=(-\mathrm{0.076}\pm \mathrm{0.229})+(\mathrm{1.002}\pm \mathrm{0.033})M_{\mathrm{e}}\left(\mathrm{HF}\right)$ and $M_{\mathrm{e}}=(\mathrm{0.795}\pm \mathrm{0.188})+(\mathrm{0.896}\pm \mathrm{0.027})M_{\mathrm{e}}\left(\mathrm{BB}\right)$, with the standard deviation of the residuals equal to 0.234 and 0.175, respectively. For the magnitude range from 6 to 8, this results in biases of 0.06 m.u. for M_e vs. M_e(HF) and varying from 0.17 to −0.04 m.u. for M_e vs. M_e(BB); i.e., our estimates are nearly unbiased relative to M_e(HF) and tend to slightly overestimate M_e(BB) at the lower end of the applicability range.

Figure 9 Comparison with energy magnitude disseminated by IRIS considering (a) M_e(HF) and (b) M_e(BB) (717 common events). The red line shows the linear regression fit, and the dotted lines show 1 standard deviation of the M_e residuals. The blue line shows line of equality for reference.

4.2 Catalog validation: role of style of faulting

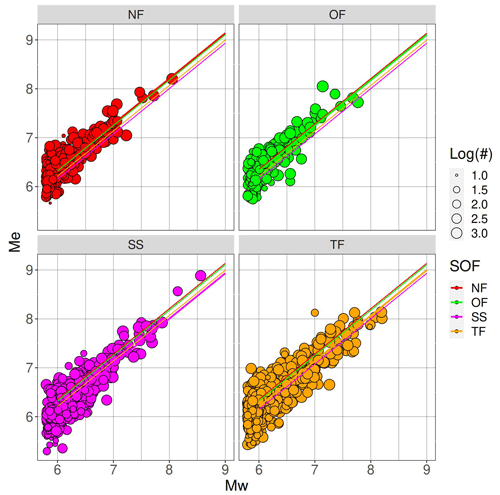
The faulting style is classified into normal, reverse, and strike slip categories, based on the plunge of the P, T, and N axes (Frohlich and Apperson, 1992), as extracted from the GEOFON moment tensor solutions. There is a normal fault (NF) if the plunge (P) ≥60°, a strike slip (SS) if the plunge (N) ≥60°, and a thrust fault (TF) if the plunge T≥50°. In the other cases, the earthquake is labeled with OF (other faulting styles). To investigate the role of the style of faulting (SOF), we separate the event term into a fixed offset for each SOF class and a perturbation term for each event. If we indicate the classes of the SOF grouping factor (corresponding to NF, SS, TF, and OF) with $k=\mathrm{1},\mathrm{2},\mathrm{3},\mathrm{4}$ and the class of event i with k_i, then the equation for the extended mixed-effects model is

$$\begin{array}{}\text{(3)}& M_{\mathrm{e}ij}=e_{\mathrm{1}}+e_{\mathrm{2}}{M}_{\mathrm{w}i}+\mathit{\delta }{S}_j+[\mathit{\delta }{\mathrm{SOF}}_{k_i}+\mathit{\delta }{E}_{{\mathrm{SOF}}_i}]+{\mathit{ϵ}}_{ij},\end{array}$$

where δSOF are the terms characterizing the average effects of the different SOF and δE_SOF are accounting for interevent differences within each SOF class (nested random effects). The standard deviations of the δS, δSOF, δE_SOF, and ϵ distributions are ϕ_S=0.190, τ_SOF=0.095, τ=0.236, and ϕ₀=0.232, respectively, generating a total standard deviation σ=0.393. The SOF terms are δSOF₁=0.098 (NF), $\mathit{\delta }{\mathrm{SOF}}_{\mathrm{2}}=-\mathrm{0.108}$ (SS), $\mathit{\delta }{\mathrm{SOF}}_{\mathrm{3}}=-\mathrm{0.045}$ (TF), and δSOF₄=0.055 (OF) (Fig. 10). The largest difference is between SS and NF, a total of 0.206 m.u. There is a systematic impact of the SOF on the intercept of the model, but the associated variability is smaller compared to the interevent variability τ (in other words, SOF effects are statistically significant, but the distributions of interevent terms separated according to faulting style are strongly overlapping).

Figure 10 M_e versus M_w categorized with SOF.

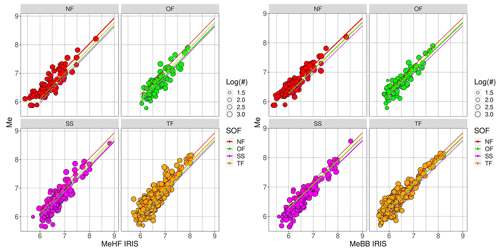
The SOF effects might arise due to physical differences (on average) between the different faulting types, e.g., due to systematically different stress drops, differences in the maturity of faults or typical environments (intra-plate vs. interplate), where different faulting types occur most often, or they might be artifacts due to the fact that the (Di Giacomo et al., 2008) method used here does not account for radiation pattern effects, and the teleseismic arrivals utilized here preferentially sample certain parts of the focal sphere. Therefore, we also investigate the role of the SOF in the relationship between M_e derived in this study and the M_e(HF) and M_e(BB) values disseminated by IRIS. We recall that the methodology implemented by IRIS accounts for radiation pattern effects, which are related to the SOF. For this analysis, the regression model is the following:

$$\begin{array}{}\text{(4)}& M_{\mathrm{e}}=g_{\mathrm{1}}+g_{\mathrm{2}}{M}_{\mathrm{iris}}+\mathit{\delta }\mathrm{SOF}+\mathit{ϵ},\end{array}$$

where M_iris is either M_e(HF) or M_e(BB). Results shown in Fig. 11 confirm that the largest intercept difference is between normal and strike slip events, and the differences in terms of magnitude units (m.u.) are also similar between the other SOF. This suggests that a large part of the SOF term is influenced by radiation pattern effects, and interpretations of these differences in terms of geodynamics or hazard potential should be done very cautiously.

Figure 11 M_e versus M_e(BB) and M_e(HF), as categorized with SOF.

5 Real-time module for SeisComP

The module, derived from me-compute has been integrated to the SeisComP package (Helmholtz Centre Potsdam GFZ German Research Centre for Geosciences and GEMPA GmbH, 2008) and has been part of the GEOFON routine real-time processing since December 2021. The first event for which M_e calculations are available and disseminated via the usual GEOFON services is https://geofon.gfz-potsdam.de/eqinfo/event.php?id=gfz2021xxzt (last access: March 2024​​​​​​​), which occurred on 7 December 2021 10:28:00.3 UTC (M_e 5.7 and M_w 5.5). The scmert add-on is available at https://github.com/SeisComP/scmert (last access: March 2024​​​​​​​).

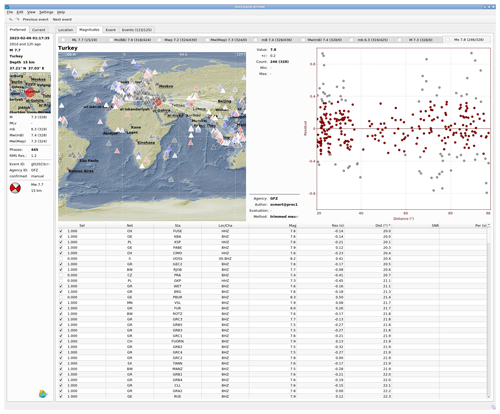
Figure 12 Screenshot of the SeisComP Origin Locator View (scolv) interactive tool for the M_w 7.7 Republic of Türkiye earthquake that occurred on 6 February 2023, 01:17 UTC along the East Anatolian Fault. The obtained network magnitude value of M_e is 7.8. Stations used are color-coded according to M_e magnitude residuals (top-left frame). Stations in gray are excluded from the network magnitude, do not match the distance range definition, or were trimmed while computing the average magnitude because they are within the ±12.5 % range. The top-right scatterplot shows M_e residuals by distance (in red those that contributed to actual M_e network magnitude). The topography shown in the map is generated using the ETOPO1 global relief model (Amante and Eakins, 2009).

The add-on has been configured in GEOFON to trigger the calculation for each origin created by the automatic processing with magnitude ≥5.5 and to compute station magnitudes M_eij for all stations according to the definition of M_e in the distance 20–98°. The scmert procedure is applied with the settings used by the GEOFON Earthquake Information Service, using stations available in real time from the GEOFON Extended Virtual Network (https://geofon.gfz-potsdam.de/eqinfo/gevn/, last access: March 2024), including station selection and the distribution trimming of 25 %. The workflow for M_e computations is as follows: as soon as an automatically detected event reaches the magnitude threshold, scmert is triggered and starts to compute M_eij upon receiving data from stations beyond 20°. The process continues until the selected window length (determined by the actual preliminary magnitude) of the last station at 98° is acquired. The first estimate of the magnitude M_e is released shortly after collecting 20 M_eij estimates from individual station, usually within a few minutes of the earthquake's origin time. SeisComP modules continue to refine the estimate until no further updates are required (this includes manual release at later stages). The computed station magnitudes M_eij are fully integrated also into the SeisComP Origin Locator View Graphical User Interface (scolv GUI; Fig. 12), with station magnitudes and residuals displayed in a dedicated energy magnitude tab.

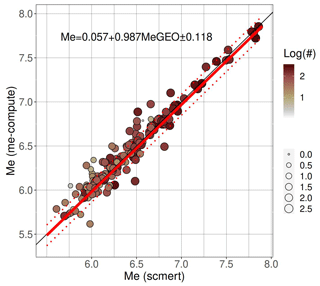
The energy magnitude values from both modules are compared in Fig. 13. We used scmert with the same settings as the GEOFON earthquake monitoring service, including station selection and trimming of the distributions. The values are in good agreement, and the best-fit model is $M_{\mathrm{e}}=\mathrm{0.057}+\mathrm{0.987}{M}_{\mathrm{e}}\left(\mathrm{GEO}\right)$, with a standard deviation of 0.118. The average difference computed for magnitudes between 6 and 8 is −0.028.

All values for M_e that have been calculated since the start of the routine processing with scmert can be accessed via the fdsnws-event web service running at GEOFON by specifying M_e as the magnitude type (i.e., https://geofon.gfz-potsdam.de/fdsnws/event/1/query?starttime=2021-12-07&magnitudetype=Me&includeallmagnitudes=true&nodata=404, last access: March 2024). These values are also disseminated to other agencies (e.g., ISC and EMSC) via the usual downstream channels, including a real-time push service.

Figure 13 Comparison between M_e computed in real time by GEOFON, with the scmert add-on for SeisComP (x axis) and offline estimation using me-compute (y axis), considering 153 common events.

6 Code and data availability

Code used for computing the energy magnitude is available from

• offline computations in me-compute https://doi.org/10.5880/GFZ.2.6.2023.008 (Zaccarelli, 2023); and

• real-time computations in SeisComP with scmert https://doi.org/10.5880/GFZ.2.4.2020.003 (Helmholtz Centre Potsdam GFZ German Research Centre for Geosciences and GEMPA GmbH, 2008).

Analyses have been performed in R (https://www.R-project.org/, R Core Team, 2020), and we used the Generic Mapping Tools (https://www.generic-mapping-tools.org/, last access: March 2024; Wessel et al., 2013) to produce Figs. 2, 5, 6, and 7. The archive, including the energy magnitude catalog (D3 and D6 in Table 1), the complete list of references for the seismic networks analyzed in this article with me-compute, and an example of the configuration files, is available from Bindi et al. (2024) (https://doi.org/10.5880/GFZ.2.6.2023.010).

7 Conclusive remarks

We computed the energy magnitude M_e for 6349 events in the moment magnitude catalog disseminated by GEOFON. When combined with M_w, M_e allows a better characterization of the tsunami and shaking potential of an earthquake. The procedure used to compile the dataset, which includes 1 031 396 M_e values for each recording station, is described in detail. Residuals are evaluated using a mixed-effects regression, which partitions the overall residuals into event-specific and station-specific contributions. These random effects are included in the distributed catalog, enabling the computation of M_e for future events and using inter-station residuals as station corrections to reduce the uncertainty in M_e. They also enable the assessment of energy magnitude adjustments for specific regions or faulting mechanisms, using interevent residuals and locating propagation anomalies with respect to the global model used to compute Green's functions using the leftover residuals. The methodology employed for computing M_e (Di Giacomo et al., 2008) is suitable for the rapid assessment of M_e (Di Giacomo et al., 2010). Therefore, it has been implemented as a module for SeisComP, allowing the automatic computation of M_e in real time and keeping the M_e catalog up to date.