SeaFlux: harmonization of air–sea CO₂ fluxes from surface pCO₂ data products using a standardized approach

Air–sea flux of carbon dioxide (CO₂) is a critical component of the global carbon cycle and the climate system with the ocean removing about a quarter of the CO₂ emitted into the atmosphere by human activities over the last decade. A common approach to estimate this net flux of CO₂ across the air–sea interface is the use of surface ocean CO₂ observations and the computation of the flux through a bulk parameterization approach. Yet, the details for how this is done in order to arrive at a global ocean CO₂ uptake estimate vary greatly, enhancing the spread of estimates. Here we introduce the ensemble data product, SeaFlux (Gregor and Fay, 2021, https://doi.org/10.5281/zenodo.5482547​​​​​​​, https://github.com/luke-gregor/pySeaFlux, last access: 9 September 2021​​​​​​​); this resource enables users to harmonize an ensemble of products that interpolate surface ocean CO₂ observations to near-global coverage with a common methodology to fill in missing areas in the products. Further, the dataset provides the inputs to calculate fluxes in a consistent manner. Utilizing six global observation-based mapping products (CMEMS-FFNN, CSIR-ML6, JENA-MLS, JMA-MLR, MPI-SOMFFN, NIES-FNN), the SeaFlux ensemble approach adjusts for methodological inconsistencies in flux calculations. We address differences in spatial coverage of the surface ocean CO₂ between the mapping products, which ultimately yields an increase in CO₂ uptake of up to 17 % for some products. Fluxes are calculated using three wind products (CCMPv2, ERA5, and JRA55). Application of a scaled gas exchange coefficient has a greater impact on the resulting flux than solely the choice of wind product. With these adjustments, we present an ensemble of global surface ocean pCO₂ and air–sea carbon flux estimates. This work aims to support the community effort to perform model–data intercomparisons which will help to identify missing fluxes as we strive to close the global carbon budget.

1 Introduction

Surface ocean partial pressure of CO₂ (pCO₂) observations plays a key role in constraining the global ocean carbon sink. This is because long-term variation in surface ocean pCO₂, ultimately driven by increases in atmospheric pCO₂ levels, is the driving force governing the exchange of CO₂ across the air–sea interface, which is commonly described through a bulk formula (Garbe et al., 2014; Wanninkhof, 2014):

$$\begin{array}{}\text{(1)}& \mathrm{Flux}=k_w\cdot \mathrm{sol}\cdot \left(p{\mathrm{CO}}_{\mathrm{2}}-p{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{atm}}\right)\cdot (\mathrm{1}-\mathrm{ice}),\end{array}$$

where k_w is the gas transfer velocity, sol is the solubility of CO₂ in seawater (in units of mol m⁻³ µatm⁻¹), pCO₂ is the partial pressure of surface ocean CO₂ (in µatm), and pCO${}_{\mathrm{2}}^{\mathrm{atm}}$ (in units of µatm) represents the partial pressure of atmospheric CO₂ in the marine boundary layer. Finally, to account for the seasonal ice cover in high latitudes, the fluxes are weighted by 1 minus the ice fraction (ice), i.e., the open ocean fraction.

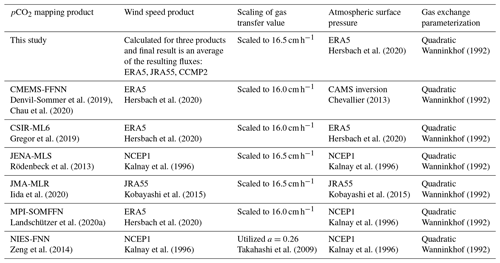
With the increasing number of observations of pCO₂ available in each new release of the Surface Ocean Carbon Dioxide Atlas (SOCAT; Bakker et al., 2016) and the adoption of various pCO₂ mapping techniques, multiple observation-based estimates of the pCO₂ field are now publicly available and updated on an annual basis. Despite these advancements, the intercomparison of the products' global and regional flux values is hindered (1) by different areal coverage and (2) by a lack of a consistent approach to calculate the air–sea CO₂ flux from pCO₂ (Table A1). These differences in flux calculations, specifically differing spatial coverage, complicate comparisons between the products and global ocean biogeochemistry models (GOBMs). In this work, we harmonize these products' flux estimates, specifically addressing three key differences between product methodologies. The resulting flux estimates can then be more directly compared to models with respect to uncertainty attribution with all sources of discrepancy attributable to the mapping method or flux calculation.

The first step addresses the variable spatial coverage of current pCO₂ products. Many of the current mapped products only cover roughly 90 % of the ocean surface, missing continental shelves and high-latitude regions. A newly released global pCO₂ climatology product (Landschützer et al., 2020b) includes coverage in the coastal and Arctic regions. We use this climatology to fill any missing areas in each individual product to create consistent full global ocean coverage.

The second methodological step is the choice of flux parameterization and appropriate scaling of wind speed data. Roobaert et al. (2018) presented uncertainty in air–sea carbon flux induced by various parameterizations of the gas transfer velocity and wind speed data products. Utilizing the MPI-SOMFFN pCO₂ product (Landschützer et al., 2020a) and a quadratic parameterization (Wanninkhof, 1992; Ho et al., 2006), they find flux estimates that diverge by 12 % depending on the choice of wind speed products. Additionally, they find regional discrepancies to be much more pronounced than global differences, specifically highlighting the equatorial Pacific, Southern Ocean, and North Atlantic as regions most impacted by the choice of wind product. Roobaert et al. (2018) stress that to minimize the uncertainties associated with the wind speed product chosen, the global coefficient of gas transfer must be individually calculated for each (Wanninkhof, 1992, 2014). In this work, we assess the impact of wind speed product choice and scaling on six pCO₂ products' calculated air–sea flux estimates. By applying a consistent flux calculation methodology to each pCO₂ product, we minimize the methodological divergence of fluxes within the ensemble.

Here, we present SeaFlux, a dataset that provides a consistent approach specifically targeting the most commonly used pCO₂ data products to deliver an end-product for intercomparisons within assessment studies such as the Global Carbon Budget (Friedlingstein et al., 2020) and the Regional Carbon Cycle Assessment and Processes (RECCAP). The SeaFlux dataset is accompanied by a Python package, called pySeaFlux (https://github.com/lukegre/pySeaFlux, last access: 9 September 2021​), that enables users to calculate fluxes for other configurations, use cases, and resolutions. Specifically, by first addressing differences in spatial coverage between the observation-based products we can better present a true global pCO₂ estimate for each product. SeaFlux also provides gas transfer velocities scaled to independent estimates of the gas transfer velocity based on the ocean ¹⁴C inventory. Further, the dataset includes estimates of atmospheric pCO₂ and the solubility of CO₂ in seawater. Finally, by calculating fluxes using multiple scaled gas transfer velocities for different wind products, we present a methodologically consistent database of air–sea CO₂ fluxes calculated from available pCO₂ products. SeaFlux is thus an ensemble data product with documented code (pySeaFlux) allowing the community to reproduce consistent flux calculations from various data-based pCO₂ reconstructions now and in the future.

2 Methods

SeaFlux is based on six observation-based pCO₂ products and spans the years 1990–2019 (Table 1). These six products include three neural-network-derived products (CMEMS-FFNN, MPI-SOMFFN, NIES-FNN), a mixed layer scheme product (JENA-MLS), a multiple linear regression (JMA-MLR), and a machine learning ensemble (CSIR-ML6). These products are included as they have been regularly updated to extend their time period and incorporate additional data that come with each annual release of the SOCAT database.

Table 1 Global area coverage and mean pCO₂ for the six observation-based products. Area coverage listed represents the average annual area covered for 1990–2019 as this value changes monthly for many products (Fig. A1). Change is defined as the filled product minus original product (i.e., a negative change implies the original product had a larger global/regional mean pCO₂ than the filled product). Global and hemispheric mean pCO₂ values for filled/original coverage are included in parentheses below the delta value.

All of these methods provide three-dimensional fields (latitude, longitude, time) of the sea surface pCO₂ and the air–sea CO₂ flux. In their original form, each product may utilize different choices for the inputs to Eq. (1) (Table A1). While the choices made by each product's creator, listed in Table A1, are not incorrect, by utilizing a uniform methodology in flux calculation, provided by pySeaFlux, the differences in the resulting flux estimate can be attributed to the pCO₂ mapping method itself. In this work we recompute the fluxes using the following inputs to the bulk parameterization approach Eq. (1): k_w is the gas transfer velocity (further discussed in Sect. 2.3); sol is the solubility of CO₂ in seawater (in units of mol m⁻³ µatm⁻¹), calculated using the formulation by Weiss (1974), near-surface EN4 salinity (Good et al., 2013), NOAA Optimum Interpolation Sea Surface Temperature V2 (OISSTv2) (Reynolds et al., 2002), and European Centre for Medium-Range Weather Forecasts (ECMWF) ERA5 sea level pressure (Hersbach et al., 2020); ice is the sea-ice fraction from NOAA OISSTv2 (Reynolds et al., 2002); pCO₂ is the partial pressure of oceanic CO₂ (in µatm) for each observation-based product after filling, as discussed in Sect. 2.1; and pCO${}_{\mathrm{2}}^{\mathrm{atm}}$ is the dry air mixing ratio of atmospheric CO₂ (xCO₂) from the ESRL surface marine boundary layer CO₂ product available at https://www.esrl.noaa.gov/gmd/ccgg/mbl/data.php (last access: 10 October 2020)​​​​​​​ (Dlugokencky et al., 2019) multiplied by ERA5 sea level pressure (Hersbach et al., 2020) at monthly resolution and applying the water vapor correction according to Dickson et al. (2007). All of the components of Eq. (1) are available in the SeaFlux dataset.

Throughout this study, flux is defined as being positive when CO₂ is released from the ocean to the atmosphere and negative when CO₂ is absorbed by the ocean from the atmosphere. In the following sections, we discuss the three steps that have the greatest impact on the inconsistencies between flux calculations in the six pCO₂ products and the approach that we utilize for the SeaFlux ensemble product.

2.1 Step 1: area filling

Machine learning methods aim to maximize the utility of the existing in situ observations by extrapolation using various proxy variables for processes influencing changes in ocean pCO₂. Extrapolation with these independently observed variables is possible due to the nonlinear relationship between pCO₂ in the surface ocean and the proxies that drive these changes. However, not all of the proxy variables have complete global ocean coverage for all months; therefore, the resulting pCO₂ products are limited by the extent of the proxy variables (Figs. 1, A1). Additionally, in continental shelf regions, there is the potential that different relationships of pCO₂ to the proxy variables are expected as opposed to in the open ocean, thus limiting the extrapolations. The mixed layer scheme (utilized by the JENA-MLS product) does not suffer from such missing areas but also does not distinguish between coastal and open ocean; it is stated to be an open ocean product which is extrapolated to the full global coverage (Rödenbeck et al., 2013). For this reason, it is not utilized in SeaFlux as a potential product for filling missing areas in the other pCO₂ products.

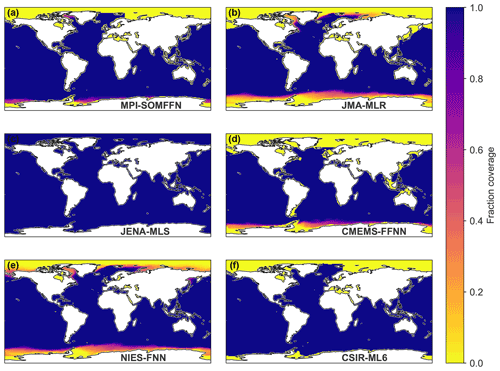
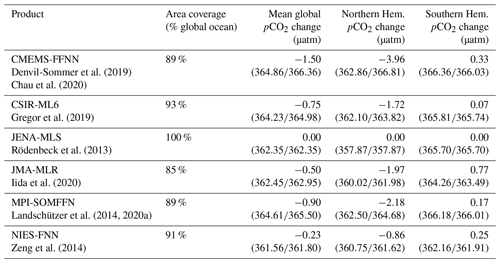
Figure 1 Maps showing the fraction of months (1990–2019) with coverage available for each of the six pCO₂ data products used in this study. Blue regions represent full temporal coverage of pCO₂ in the product, while yellow areas show regions with no reported pCO₂ values for any month of the time series.

To account for differing area coverage, past studies (Friedlingstein et al., 2019, 2020; Hauck et al., 2020) have adjusted observation-based flux products by simply scaling their global flux based on the percent of the total ocean area represented (Fig. A2). This does not account for the fact that some areas have CO₂ flux densities that are higher or lower than the global average, and their adjustment would be based on that mean value (Tables 1, 3). Thus, the magnitude of the adjustment by area-scaling is likely an underestimate in some years or products (McKinley et al., 2020). One specific example is the northern high latitudes where coverage by the six products varies substantially. Similarly, three products provide estimates in marginal seas such as the Mediterranean, while the other three products have no reported pCO₂ values here.

To address the inconsistent spatial coverage in products we utilize a newly released open and coastal merged climatology product (MPI-ULB-SOMFFN; Landschützer et al., 2020b, c) that is a blend of the coastal ocean SOMFFN mapping method (Laruelle et al., 2017) and the open ocean equivalent (MPI-SOMFFN; Landschützer et al., 2020a). The merged product includes full coverage of open ocean pCO₂ along with coastal ocean regions, marginal seas, and the Arctic Ocean at 1^∘ by 1^∘ or finer spatial resolution. A potential alternative resource for filling the missing regions is the OceanSODA-ETHZ surface pCO₂ product (Gregor and Gruber, 2021) that maps both the open ocean and marginal seas explicitly for the period 1985–2018 (unlike the JENA-MLS approach). However, as with other products, OceanSODA-ETHZ has limited coverage in the Arctic. A comparison of the overlapping regions between the MPI-ULB-SOMFFN and OceanSODA-ETHZ products shows good agreement (Fig. A3). We have confidence moving forward using solely MPI-ULB-SOMFFN for area-filling, as including OceanSODA-ETHZ would not result in substantially different results and would be constrained by its limited Arctic coverage.

For each observation-based product, we fill missing grid cells with a scaled value based on the global-coverage MPI-ULB-SOMFFN climatology (Fig. 2). The scaling accounts for year-to-year changes in pCO₂ in the missing areas (given that the extended MPI-ULB-SOMFFN product is a monthly climatology centered on the year 2006) and is obtained as follows.

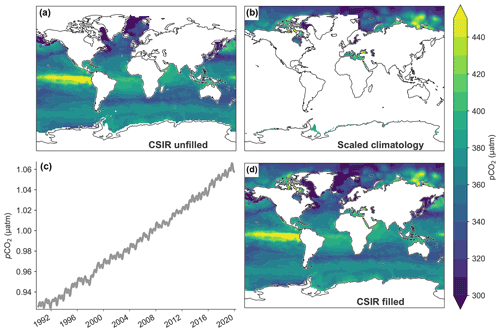
Figure 2 Maps demonstrating the filling procedure employed in this study using a snapshot of pCO₂ from May 2013. (a) Map of unfilled CSIR-ML6 pCO₂. (b) The scaled pCO₂ climatology of Landschützer et al. (2020b). (c) The mean pCO₂ for the scaled climatology over time. (d) The CSIR-ML6 pCO₂ product (a) filled using the scaled climatology (b).

To extend the open and coastal merged climatology (MPI-ULB-SOMFFN) to 1990–2019, we calculate a global scaling factor based on the product-based ensemble mean pCO₂ for regions that are covered consistently by all six pCO₂ products. We first mask all pCO₂ products to a common sea mask before taking an ensemble mean (pCO${}_{\mathrm{2}}^{\mathrm{ens}}$). Next, we divide this ensemble mean by the MPI-ULB-SOMFFN climatology (pCO${}_{\mathrm{2}}^{\mathrm{clim}}$) at monthly 1^∘ by 1^∘ resolution (Eq. 2). The monthly scaling factor (sf${}_{p{\mathrm{CO}}_{\mathrm{2}}}$) is calculated by taking the mean over the spatial dimensions. An alternative method of calculating the scaling factor individually for each pCO₂ product yields very similar results; the benefit of the ensemble approach is that it allows for the scaling factor to be quickly utilized for any other pCO₂ product under development.

The scaling factor calculation can be represented as

$$\begin{array}{}\text{(2)}& {\mathrm{sf}}_{p{\mathrm{CO}}_{\mathrm{2}}}={\mathrm{mean}}_{x,y}\left({\displaystyle \frac{p{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{ens}}}{p{{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{clim}}}}\right),\end{array}$$

where sf${}_{p{\mathrm{CO}}_{\mathrm{2}}}$ is the one-dimensional scaling factor (time dimension), pCO${}_{\mathrm{2}}^{\mathrm{ens}}$ is the ensemble mean of all pCO₂ products at three dimensions, monthly 1^∘ by 1^∘ resolution, pCO${}_{\mathrm{2}}^{\mathrm{clim}}$ is the MPI-ULB-SOMFFN climatology, also at three dimensions but limited to just one climatological year. The x and y indicate that we take the area-weighted average over longitude (x) and latitude (y) resulting in the monthly one-dimensional scaling value. If a product mean is exactly equal to the climatology mean, the scaling factor is 1. The value ranges from 0.91 to 1.06 over the 30-year period. The one-dimensional scaling factor is then multiplied by the MPI-ULB-SOMFFN climatology for each spatial point resulting in a three-dimensional scaled filling map. These values are then used to fill in missing grid cells in each observation-based product.

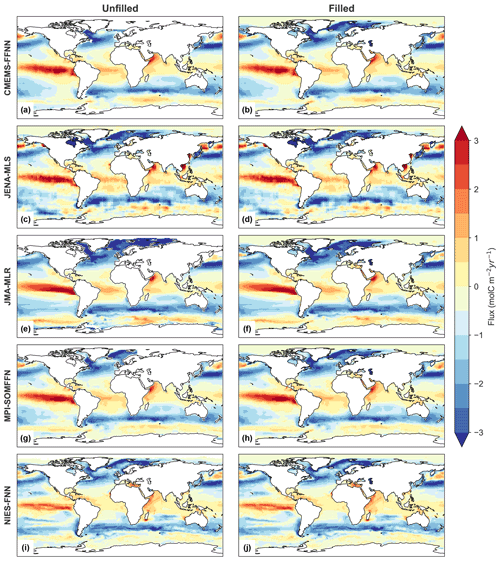
Globally, the area-filling adjustments result in a difference of less than 17 % of the total flux in all products, with the mean adjustment for the six products at 8 %. In the Northern Hemisphere, however, the filling process can drive adjustments of up to 32 % due to missing coverage in the North Atlantic specifically (Fig. 1, Table 3). As expected, the observation-based products with more complete spatial coverage tend to have smaller flux adjustments. However, the impact on the final CO₂ flux depends on both the ΔpCO₂ and wind speed of the areas being filled (Figs. 2–3, Tables 1, 3). The only product that does not change during this adjustment process is the JENA-MLS mixed-layer scheme-based product (Rödenbeck et al., 2013) which is produced with full spatial coverage and therefore needs no spatial filling; any difference between filled/unfilled for this product is due to the ocean mask applied in SeaFlux.

Figure 3 Mean flux (mol m⁻² yr⁻¹) for 1990–2019 for CSIR-ML6 product. (a) Map of mean-calculated flux using the original pCO₂ product and three scaled wind products (CCMPv2, ERA5, JRA55); (b) map of mean-calculated flux using the filled pCO₂ product and three scaled wind products. Similar maps for all other products are available in Fig. A5.

Our approach is not without its own assumptions and limitations. We rely on a single estimate to fill the missing pCO₂ given that this is the only publicly available coastal-resolution product currently existing. Nevertheless, the fact that common missing areas along coastal regions and marginal seas are reconstructed using specific coastal observations provides a step forward from the linear-scaling approach currently used by the Global Carbon Budget (Friedlingstein et al., 2019, and Fig. A2 in Friedlingstein et al., 2020). Further confidence is provided by previous research showing that climatologically relevant signals, i.e., mean state and seasonality, are well reconstructed by the MPI-SOMFFN method (Gloege et al., 2021).

Furthermore, our scaled filling methodology assumes that pCO₂ in the missing ocean regions is increasing at the same rate as the common area of open ocean pCO₂ used to calculate the scaling factor. Research from coastal ocean regions and shelf seas reveal that, in spite of a large spatial heterogeneity, this is a reasonable first-order approximation (Laruelle et al., 2018).

Any method of artificially filling in missing areas introduces additional uncertainty to the flux estimates. However, this introduced uncertainty is necessary for true global intercomparison efforts. A concern is that the filling method would artificially lower the spread of the products in the SeaFlux ensemble. We do not find this to be the case. The standard deviation of the mean flux for a most conservative mask, which includes only those grid cells with values reported for all six pCO₂ products for all months, is nearly identical to the standard deviation of the final version of the SeaFlux product ensemble. This comparison indicates that our filling method does not in fact artificially lower the uncertainty or decrease the spread of the products.

2.2 Step 2: wind product selection

Historical wind speed observations (including measurements from satellites and moored buoys) are aggregated and extrapolated through modeling and data assimilation systems to create global wind reanalyses. These reanalyses are required to compute air–sea gas exchange. Air–sea flux is commonly parameterized as a function of the gradient of CO₂ between the ocean and the atmosphere with wind speed modulating the rate of the gas exchange (Eq. 1). Each of these wind reanalyses has strengths and weaknesses, specifically on regional and seasonal scales (Chaudhuri et al., 2014; Roobaert et al., 2018; Ramon et al., 2019), but all are considered reasonable options by the community (Roobaert et al., 2018). The pySeaFlux package includes options for the user to select their wind product of choice. For the SeaFlux ensemble product, we use three wind reanalysis products for completeness: the Cross-Calibrated Multi-Platform v2 (CCMP2; Atlas et al., 2011), the Japanese 55-year Reanalysis (JRA-55; Kobayashi et al., 2015), and the European Centre for Medium-Range Weather Forecasts (ECMWF) ERA5 (Hersbach et al., 2020). The wind speed (U₁₀) is calculated at the native resolution of each wind product from u and v components of wind. Details of each wind product are shown in Table A2.

2.3 Step 3: calculation of gas transfer

We employ the quadratic wind speed dependence (Wanninkhof, 1992; Ho et al., 2006) and calculate the gas transfer velocity (kw) for each of the wind reanalysis products as

$$\begin{array}{}\text{(3)}& k_w=a\cdot \langle U^{\mathrm{2}}\rangle \cdot {\left({\displaystyle \frac{\mathrm{Sc}}{\mathrm{660}}}\right)}^{-\mathrm{0.5}},\end{array}$$

where the units of k_w are in centimeters per hour (cm h⁻¹), Sc is the dimensionless Schmidt number, and 〈U²〉 denotes the square of average 10 m high winds (m s⁻¹), also referred to as the second moment of the wind speed. We choose the quadratic dependence of the gas transfer velocity as it is widely accepted and used in the literature (Wanninkhof, 1992; Ho et al., 2006); however, we acknowledge that the actual relationship could vary from less than linear (Krakauer et al., 2006) to cubic (Wanninkhof and McGillis, 1999; Stanley et al., 2009). Observational and modeling studies have often suggested that different parameterizations could be more appropriate under specific conditions such as in regions of high wind speeds (Fairall et al., 2000; Nightingale et al., 2000; McGillis et al., 2001; Krakauer et al., 2006); recent direct carbon dioxide flux measurements made in the high-latitude Southern Ocean confirm that even in this high wind environment, a quadratic parameterization fits the observations best (Butterworth and Miller, 2016). Future updates of SeaFlux will include k_w for other parameterizations (e.g., cubic).

We calculate the square of the wind speed at the native resolution of each wind product and then average it to 1^∘ by 1^∘ monthly resolution (see Table A2). The order of this calculation is important as variability is lost when resampling data to lower resolutions because of the concavity of the quadratic function. For example, taking the square of time-averaged wind speeds would result in an underestimate of the gas transfer velocity (Sarmiento and Gruber, 2006; Sweeney et al., 2007). The resulting second moment is equivalent to $\mathit{<}{U}^{\mathrm{2}}\mathit{>}=U_{\mathrm{mean}}^{\mathrm{2}}+U_{\mathrm{std}}^{\mathrm{2}}$, where U_mean and U_std are the temporal mean and standard deviation calculated from the native temporal resolution of U.

In addition to the choice of wind parameterization (Roobaert et al., 2018), large differences in flux can result due to the scaling of the coefficient of gas transfer (a) applied when calculating the global mean gas transfer velocity. This constant originates from the gas exchange process studies (Krakauer et al., 2006; Sweeney et al., 2007; Müller et al., 2008; Naegler, 2009) which utilize observations of radiocarbon data from the GEOSECS and WOCE/JGOFS expeditions (Key et al., 2004). The ¹⁴C released from nuclear bomb testing (hence bomb-¹⁴C) in the mid-20th century has since been taken up by the ocean. The number of bomb-¹⁴C atoms in the ocean, relative to the pre-bomb ¹⁴C, can thus be used as a constraint on the long-term rate of exchange of carbon between the atmosphere and the ocean. This coefficient, a, is not consistent for each wind product and must thus be individually calculated via the equation based on equation 39 from Naegler (2009):

$$\begin{array}{}\text{(4)}& a=k_w\cdot \langle U^{\mathrm{2}}{\rangle }^{-\mathrm{1}}\cdot {\left({\displaystyle \frac{\mathrm{Sc}}{\mathrm{660}}}\right)}^{\mathrm{0.5}},\end{array}$$

the parameters of which are defined in Eq. (3). The units of the coefficient a are (cm h⁻¹) (m s⁻¹)⁻². In the cost function, a global average of k_w is set for which several estimates exist in the literature (ranging from 15.1 to 18.2 cm h⁻¹), introducing another source of uncertainty as shown in Table A1 (Krakauer et al., 2006; Naegler et al., 2006; Sweeney et al., 2007; summarized in Table 2 of Naegler, 2009). Naegler (2009) show that these estimates fall within the ∼20 % range of uncertainty of the bomb-¹⁴C-constrained global average k_w, which they estimate at 16.5 ± 3.2 cm h⁻¹. We scale k_w to this single value (16.5 cm h⁻¹) over the three-decade period 1990–2019.

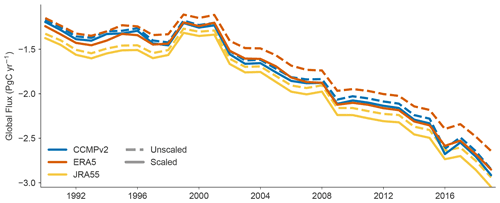
Our scaled coefficients (Table 2) correspond well with the estimate of Wanninkhof (2014) who uses the CCMP wind product to estimate a as 0.251, whereas our estimate of a for CCMP is 0.257. Scaling k_w to a single global value (here, 16.5 cm h⁻¹) for all wind products reduces the spread of flux estimates, but it does not reduce the uncertainty which remains ∼20 %. This uncertainty must be accounted for when reporting fluxes (Naegler, 2009; Wanninkhof, 2014). In this work, we refer to this uncertainty, which is inherent to the formulation and scaling of k_w, as intrinsic uncertainty, which we do not try to reduce with SeaFlux and include in our reported uncertainty estimate. However, by correctly scaling k_w for each wind product we reduce the disharmony associated with incorrect scaling by up to 9 %, depending on which pCO₂ and wind reanalysis products are considered. This is consistent with previous results shown by Roobaert et al. (2018, 2019).

Table 2 CSIR-ML6 product flux values. Column 1 lists the scaled coefficient of gas transfer for each of the three wind reanalysis products. Column 2 includes the global mean flux using each wind product. Column 3 shows the difference in resulting flux when using a scaled coefficient of gas transfer versus a set value of 0.26. All flux values reported are from the area-filled product version. All values are computed over the period 1990–2019.

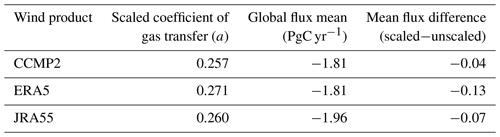
Table 3 Mean air–sea fluxes (PgC yr⁻¹) for 1990–2019 using the mean of three wind products, calculated for the filled global area and the unfilled native “global” area for each pCO₂ product. The Northern Hemisphere (NH) and Southern Hemisphere (SH) fluxes (unfilled/filled) are included to highlight the imbalanced regional effect of the spatial filling process.

2.4 Further parameters for flux calculation

The remaining parameters of Eq. (1) are the solubility of CO₂ in seawater (sol), the atmospheric partial pressure of CO₂ (pCO${}_{\mathrm{2}}^{\mathrm{atm}}$), and the area weighting to account for sea-ice cover. While the choices of products used for these parameters can also result in differences in flux estimates, the impacts are much smaller as compared with the parameters discussed above.

Atmospheric pCO₂ is calculated as the product of surface xCO₂ and sea level pressure corrected for the contribution of water vapor pressure. The choice of the sea level pressure product or absence of the water vapor correction can have a small, but not insignificant, impact on the calculated fluxes. Additionally, some products utilize the output of an atmospheric CO₂ inversion product (e.g., CarboScope, Rödenbeck et al., 2013; CAMS CO₂ inversion, Chevallier, 2013) which can introduce differences in the flux estimate outside of the sources related to a product's surface ocean pCO₂ mapping method. Importantly, we do not advocate that our estimate of pCO${}_{\mathrm{2}}^{\mathrm{atm}}$ is an improvement over other estimates thereof; rather we provide an estimate of pCO${}_{\mathrm{2}}^{\mathrm{atm}}$ that has few assumptions and leads to a methodologically consistent estimate of ΔpCO₂. We maintain the same philosophy in our estimates of the solubility of CO₂ in seawater and sea-ice area weighting, and therefore we do not elaborate on them here.

3 Results and discussion

3.1 SeaFlux air–sea CO₂ flux calculation

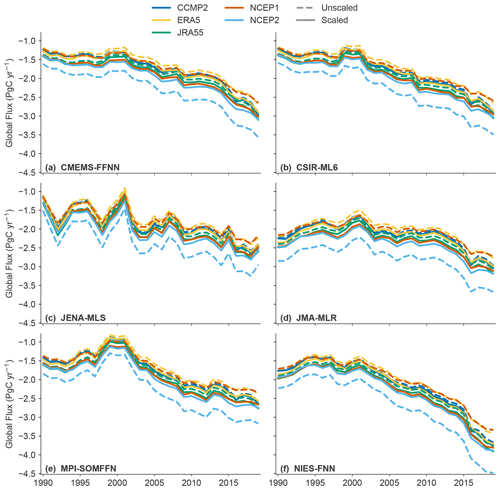
Following Eq. (1), CO₂ flux is calculated individually for each of the six observation-based products with three available wind products (CCMPv2, ERA5, JRA55), as discussed in Sect. 2.2 (Table 4). Since we account for spatial coverage differences via our filling method (Sect. 2.1), taking a global mean flux for each of the data products truly follows the definition of “global” for each original product. Figure 4 shows the difference these wind products generate on the resulting global mean flux of the CSIR-ML6 product as one example (other products in Fig. A4). The three wind products show consistent fluxes throughout the time series, with the importance of appropriate scaling of the coefficient of gas transfer (a) evident in the significant differences between global mean fluxes calculated with unscaled and scaled a values (Fig. 4, Table 2). It is clear that the impact of applying the appropriate coefficient of gas transfer through proper scaling has an impact on the resulting flux time series.

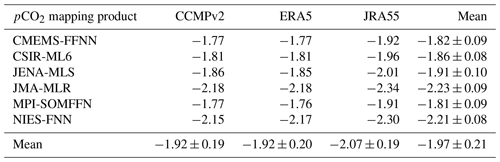
Table 4 Mean fluxes (PgC yr⁻¹) for each observational pCO₂ product over the period 1990–2019. Mean flux is calculated from filled coverage pCO₂ map and scaled gas exchange coefficient; global mean flux is for three wind products (CCMP2, ERA5, JRA55) and the average. The time series of the mean flux values for each product (rightmost column) are plotted in Fig. 5.

Figure 4 CSIR-ML6-calculated air–sea CO₂ flux time series for various wind speed products, scaled (solid) and unscaled (dashed; a=0.251). Time series plots for all pCO₂ products and including two additional wind products (NCEP1 and NCEP2) are included in Fig. A4.

3.2 SeaFlux ensemble flux

By calculating each product's air–sea CO₂ flux using consistent inputs described in Sect. 3.1, a more accurate comparison of fluxes with the SeaFlux ensemble is permitted. Combining all fluxes, we derive a mean flux estimate of −1.97 ± 0.45 PgC yr⁻¹ (Tables 4, A3). We discuss the calculation of the uncertainty in the following section. This flux estimate is strengthened by the use of multiple observation-based pCO₂ products and wind products which we consider to be independent estimates for the purpose of the uncertainty calculation. These flux values are different from those produced by the observation-based pCO₂ product's original creator, both spatially and on the mean (Figs. 5, A5, Tables A1, A3). However, by calculating fluxes in such a consistent manner, we on the one hand gain more confidence in the ensemble mean estimate as it considers representations using a variety of pCO₂ reconstructions, gas transfer parametrizations, and wind products, and on the other hand, we have a more realistic uncertainty representation than previous estimates based on a single pCO₂ reconstruction.

Figure 5 Global flux time series from six observation-based products. Color lines show fluxes calculated from the standardized approach presented here (spatial filling with flux is calculated from three wind products, and the average flux is then plotted here); the black line shows the mean of six products. The shaded region shows the spread of original flux calculations from product creators with the mean in gray.

3.3 Uncertainty discussion

All flux estimates using such parameterizations are not without significant uncertainties, and SeaFlux is no exception. We estimate the uncertainty of the flux estimate to be 0.45 PgC yr⁻¹. Here, the stated spread represents $\sqrt{\sum ({\mathit{\sigma }}_{\mathrm{wind}}^{\mathrm{2}},{\mathit{\sigma }}_{p{\mathrm{CO}}_{\mathrm{2}}}^{\mathrm{2}},{\mathit{\sigma }}_{\mathrm{kw}}^{\mathrm{2}})}$, where ${\mathit{\sigma }}_{p{\mathrm{CO}}_{\mathrm{2}}}$ (0.19 PgC yr⁻¹) is the mean standard deviation over the six filled pCO₂ products, σ_wind (0.09 PgC yr⁻¹) is the mean standard deviation over the three wind products included in the SeaFlux product, and ${\mathit{\sigma }}_{\mathrm{kw}}^{\mathrm{2}}$ (0.39 PgC yr⁻¹) is the 20 % uncertainty in the gas transfer velocity and associated scaling flux parameterization (Wanninkhof, 2014). This last estimate shows that there is significant intrinsic uncertainty inherent to the method of calculation, as estimated by Naegler (2009) and Wanninkhof (2014).

Currently, there is only one product available designed to estimate the pCO₂ of coastal oceans, the Arctic Ocean, and marginal seas, and this has the potential to cause an underestimation of ${\mathit{\sigma }}_{p{\mathrm{CO}}_{\mathrm{2}}}$. It would be beneficial to likewise have an ensemble of estimates in these regions to better constrain the uncertainty attached to this filling approach. Therefore, while our current analysis shows that the chosen filling method does not itself reduce the spread in the products, we push the community to extend their products to the coastal ocean so as to eliminate the need for this correction in the future.

While the SeaFlux product is unable to further reduce these sources of uncertainty, the strength of the product is that it provides an estimated flux with no source of difference that is not implicit in the mapping method or flux calculation.

3.4 Issues not addressed by SeaFlux

While SeaFlux presents one approach to standardize the calculation of air–sea carbon flux, there remain issues that the ocean carbon community is still working towards understanding and incorporating. One such issue has been raised by Watson et al. (2020) who contend that a correction should be applied to in situ pCO₂ observations to account for the vertical temperature gradient between the ship water intake depth and the surface skin layer where gas exchange actually takes place. A further correction should be applied when calculating fluxes to account for the “cool skin” effect caused by evaporation (Woolf et al., 2016; Watson et al., 2020). Applying these corrections results in an increasing CO₂ sink by up to 0.9 PgC yr⁻¹ (Watson et al., 2020). Here, we do not take such adjustments into account for two reasons. Firstly, the skin temperature correction to pCO₂ needs to be applied directly to the measurements and not the final interpolated pCO₂ from the data products. Hence, it is up to the developers of the SOCAT dataset and the developers of the pCO₂ mapping products to decide on the inclusion of this correction. It would then be up to the developers of the data products to update their mapped products. Secondly, the cool skin correction would be equally applied to all methods and would not contribute to the inconsistencies in flux calculation that we are trying to address here. As the ocean carbon community moves towards consensus on such issues, SeaFlux will be updated to include revised protocols.

To compare these estimates of contemporary air–sea net flux (Fnet) from surface ocean pCO₂ with estimates of the anthropogenic carbon flux from interior data (Mikaloff Fletcher et al., 2006; DeVries, 2014; Gruber et al., 2019) or from global ocean biogeochemical models (Friedlingstein et al., 2020; Hauck et al., 2020), it is necessary to account for the outgassing of natural carbon, which was supplied to the ocean by rivers, as well as the non-steady-state behavior of the natural carbon cycle (Hauck et al., 2020). Work is ongoing to quantify the lateral river carbon flux transported into the coastal and open oceans. Current estimates are 0.23 PgC yr⁻¹ (Lacroix et al., 2020), 0.45 PgC yr⁻¹ (Jacobson et al., 2007), and 0.78 PgC yr⁻¹ (Resplandy et al., 2018), and the regional distribution of the resulting outgassing remains understood only from a few model simulations (Aumont et al., 2001; Lacroix et al., 2020). In addition, quantification of non-steady-state behavior of the natural carbon cycle has only recently been proposed, and significant uncertainty remains, with a magnitude range of 0.05–0.4 PgC yr⁻¹ for 1994–2007 (Gruber et al., 2019; McKinley et al., 2020). Similar to the cool skin correction suggested by Watson et al. (2020) discussed above, in this work we have not included these adjustments here as they would not contribute to the inconsistencies between the different products for Fnet itself, which is our focus.

4 Code and data availability

Data (Gregor and Fay, 2021) are available on Zenodo (https://doi.org/10.5281/zenodo.5482547), and the software used to generate these data is available on GitHub (https://github.com/lukegre/pySeaFlux, last access: 9 September 2021). NOAA_OI_SST_V2 data are provided by the NOAA/OAR/ESRL PSL, Boulder, Colorado, USA (Reynolds et al., 2002, https://doi.org/10.1175/1520-0442(2002)015<1609:AIISAS>2.0.CO;2).

5 Conclusions

We introduce SeaFlux, a dataset that facilitates a standardized approach for flux calculations from observation-based pCO₂ products. Specifically, we address the two largest sources of divergence in air–sea flux calculation, namely the differences in spatial coverage between the products and the scaling of the gas transfer velocity for available wind speed products based on global ¹⁴C-based constraints. The area adjustment is the largest contributor to the methodological discrepancies, resulting in an increase in CO₂ uptake of 0 %–17 % relative to the original, possibly incomplete coverage (depending on pCO₂ product). The global scaling of the gas transfer velocity can change the CO₂ flux on average by 5 % relative to non-standardized flux calculations. The impact of applying the appropriate gas exchange coefficient through proper scaling has a larger impact on the resulting flux time series than solely the choice of wind product. By accounting for these sources of differences, the global mean-calculated air–sea carbon flux calculated from the six available products is adjusted by up to 21 %. The SeaFlux ensemble mean air–sea carbon flux is estimated to be −1.97 ± 0.45 PgC yr⁻¹ with the spread representing 1σ as calculated from the 18 realizations.

This work provides an ensemble data product of the air–sea CO₂ flux predicated on observation-based pCO₂ products. This ensemble product is meant to facilitate the use of the pCO₂ observation-based ocean flux estimates in assessment studies of the global carbon cycle, such as the Global Carbon Budget or RECCAP-2. Note that the original pCO₂ products still offer additional information important in other applications, such as coverage over longer time periods, higher spatial or temporal resolution, or runs incorporating further auxiliary datasets or pCO₂ data (e.g., SOCCOM float data; Bushinsky et al., 2019).

Along with the ensemble of CO₂ flux fields, we also provide a public-use coding package (pySeaFlux) allowing users to apply the presented standardized flux calculations to their own data-based pCO₂ reconstructions.

Appendix A

Table A1 Summary of parameters used to calculate flux.

Table A2 Summary of wind products used in this study. Note that the date range starts for the first full year of data. We do not use NCEP1/2 in our main results, but these are included for reference. Time units are in hours and space in degrees. Mean wind speed is given for the ice-free ocean for the three-decade period 1990–2019.

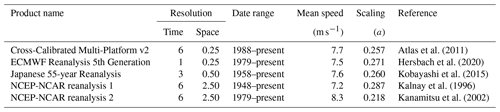
Table A3 Mean fluxes (PgC yr⁻¹) for 1990–2019 for each observational pCO₂ product. Mean flux calculated from unfilled (filled) coverage pCO₂ map and unscaled/scaled coefficient of gas transfer (unscaled = 0.251), calculated for three wind products (CCMP2, ERA5, JRA55) with the average shown here. Percent change is calculated as the difference between the unfilled–unscaled and filled–scaled as a fraction of the filled–scaled; it does not indicate an error in the product's flux but is a representation of the impact the filling and scaling can have on the end flux estimate. The mean flux as reported in the original pCO₂ product is included for comparison (Fig. 5).

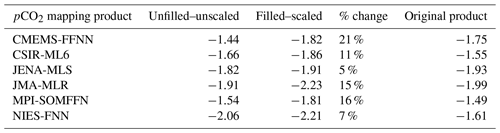
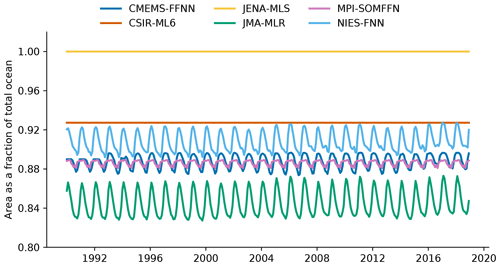
Figure A1 Time series showing the fraction of area covered by observations as a function of time (monthly) for the six pCO₂ data products used in this study.

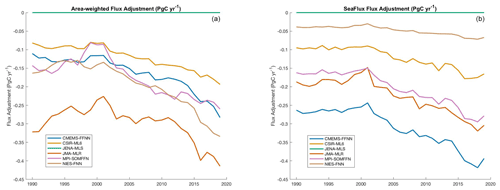
Figure A2 Annual time series of the additional flux amount calculated by the area-weighted method used in the Global Carbon Budget (a) and a similar plot showing the annual additional flux using the SeaFlux methodology (b).

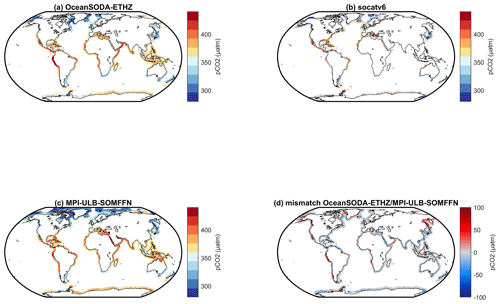
Figure A3 Spatial distributions of the annual mean pCO₂ (µatm) generated by (a) ETHZ-OceanSODA, (b) extracted from the SOCATv6 database, and (c) from the MPI-ULB merged product. (d) Bias between panels (a) and (c) (in µatm; red colors correspond to regions in which the pCO₂ from ETHZ-OceanSODA is higher than the MPI-ULB merged product). There is good agreement between the products on a regional scale.

Figure A4 Air–sea CO₂ flux time series (PgC yr⁻¹) calculated using five wind speed products (CCMPv2, ERA5, JRA55, NCEP1, NCEP2), scaled (solid) and unscaled (dashed).​​​​​​​

Figure A5 Mean flux (mol m⁻² yr⁻¹) for 1990–2019. Left-hand column: map of mean-calculated flux using the unfilled pCO₂ product and three scaled wind products. Right-hand column: map of mean-calculated flux using the filled pCO₂ product and three scaled wind products.