Meteorological drought lacunarity around the world and its classification

The measure of drought duration strongly depends on the definition considered. In meteorology, dryness is habitually measured by means of fixed thresholds (e.g. 0.1 or 1 mm usually define dry spells) or climatic mean values (as is the case of the standardised precipitation index), but this also depends on the aggregation time interval considered. However, robust measurements of drought duration are required for analysing the statistical significance of possible changes. Herein we climatically classified the drought duration around the world according to its similarity to the voids of the Cantor set. Dryness time structure can be concisely measured by the n index (from the regular or irregular alternation of dry or wet spells), which is closely related to the Gini index and to a Cantor-based exponent. This enables the world’s climates to be classified into six large types based on a new measure of drought duration. To conclude, outcomes provide the ability to determine when droughts start and finish. We performed the dry-spell analysis using the full global gridded daily Multi-Source Weighted-Ensemble Precipitation (MSWEP) dataset. The MSWEP combines gauge-, satellite-, and reanalysis-based data to provide reliable precipitation estimates. The study period comprises the years 1979–2016 (total of 45 165 d), and a spatial resolution of 0.5^∘, with a total of 259 197 grid points. The dataset is publicly available at https://doi.org/10.5281/zenodo.3247041 (Monjo et al., 2019).

1 Introduction

Drought depends mainly on the sector affected and the timescale considered (Wilhite and Glantz, 1985; Crausbay et al., 2017). Focusing on the timescale, we usually distinguish between dry spells (daily timescale) and negative anomalies, commonly represented by monthly or yearly indices such as the standardised precipitation index, the standardised evapotranspiration index, or the Palmer drought severity index, among others (Vicente-Serrano et al., 2010, 2015). Alternation between dry and wet events presents self-similarity (characteristic of fractal objects) in the same manner that the Cantor set alternates points with gaps (Martínez et al., 2007; Feng et al., 2015; Dayeen and Hassan, 2016; Lucena et al., 2018). According to Mandelbrot, fractality can be found by measuring. He noted that, the more accurate the measurement ruler, the more infinite the British coastline appears to be, since the immeasurable curves of the coast situate it between a line (one dimension) and a surface (two dimensions), i.e. with a fractal or fractional dimension (Mandelbrot, 1967).

A commonly used method for measuring the dimension of fractal objects involves box counting, which is similar to using a ruler for measuring a coastline. Given an object embedded in an N volume (N=1, length; N=2, area; N=3, volume; etc.), the method consists of covering the object several times, using unitary (N−1)-volume boxes of different sizes r for each completed covering, and counting how many covering boxes are required in each case (Olsson et al., 1992; Sakhr and Nieminen, 2018). As the box size becomes smaller, the total (N−1) volume of the fractal object tends towards the infinite rather than converging towards a finer value, and the N volume is zero. For instance, the Cantor set is embedded in the [0, 1] segment with infinite (zero-dimensional) points, but its total (one-dimensional) length is zero. Formally, an object (embedded in an N volume) possesses a fractal (non-integer) dimension B between N−1 and N if a well-defined B volume V=M_rr^B exists, where M_r is the number of boxes with size r (Imre and Bogaert, 2006). A well-defined B volume means that V and B remain constant for small values of r.

Another related measure involves the Lyapunov exponent, which indicates the rate of separation of infinitesimally close trajectories, or involves the inverse, sometimes referred to as Lyapunov time, since it indicates the time expected to become a chaotic trajectory (Boeing, 2016; Kuznetsov, 2016; Gaspard, 2005; Bezruchko and Smirnov, 2010). The Hurst exponent is also related to the fractal dimension of chaotic time series, providing possible long-term memory throughout autocorrelation (Mandelbrot, 1985; Feder, 1988; Yu et al., 2015).

The fractal behaviour of dry spells can be observed in Richardson's log–log plot of cumulative dry durations with regard to different unit durations (Sen, 2008; Meseguer-Ruiz et al., 2017). Similarities with the Cantor set (positive Lyapunov exponents) were found for dry-spell sequences in Europe (Lana et al., 2010). In this sense, dry pauses of the rainfall can be compared with the gap distribution of fractal objects, which is also known as lacunarity (Martínez et al., 2007; Lucena et al., 2018). The lacunarity analysis is used to characterise “spatial” patterns (such as invariance, density, and heterogeneity) of fractal objects, which represent attractor solutions of nonlinear dynamical systems (Plotnick et al., 1996; Wilkinson et al., 2019). If a time series of precipitation is a solution of the climatic system at a given point, the dryness distribution informs (climate) average features of the system (e.g. surface convergences or divergences of moisture flows and latent energy fluxes or speed of the hydrological cycle).

According to a multifractal analysis of the standardised precipitation, power-law decay distribution describes well the probability density function of return intervals of drought events (Hou et al., 2016). The Hurst exponent was also used to analyse the fractal persistence of the Palmer drought severity index, providing values close to 1 (i.e. long-term positive autocorrelation) throughout Turkey (Tatli, 2015). The concept of persistence of dryness is used by some authors as an early indicator of drought, according to the upper-order Markov chain model (Martín-Vide and Gomez, 1999; Lana et al., 2018; López de la Franca Arema et al., 2015).

In addition, the fractal density of wet (or dry) spells can be estimated according to the n index (Monjo, 2016). This index measures the persistence of records (or lengths) of a sequence of wet (or dry) spells similarly to how regularity is measured in a Lorenz curve, whilst preserving the time structure of the events. A value of n<0.5 implies that a time series is persistent (consecutive similar values), while for n>0.5 the time series is anti-persistent. This regularity measure is closely related to the Shannon entropy, the Gini index (G), and the box-counting dimension of rainfall (Monjo, 2016; Monjo and Martin-Vide, 2016). For this reason, the n index constitutes the main measure chosen in our work for analysing drought lacunarity around the world, also compared with a Cantor-based exponent (C_e).

2 Methods

2.1 Dry-spell n index

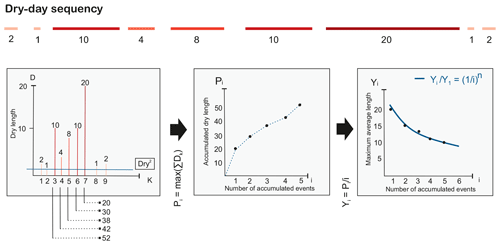
The main fractal measure was estimated for dry-spell density by means of the n index. In a similar way to the n index, which describes the decrease rate (power law) of the maximum average intensities of rainfall over time (within a particular meteorological event), it also can be applied to analyse how dry-spell lengths decrease around a maximum value. For this propose, each spell duration D_i was taken as a precipitation value, considering the minimum value D₀=1 to be the dry value by definition. For instance, let $D=(\mathrm{3},\mathrm{4},\mathrm{7},\mathrm{1},\mathrm{3},\mathrm{10},\mathrm{12})$ be a time series of consecutive dry spells. Subsequently, two independent events (spells of spells) are built around the dry value (D₀=1) as (3, 4, 7), (3, 10, 12) (Fig. A2). In the present study, only dry spells were considered for building events; thus, each separated event is referred to as a dry-spell spell (DSS).

In a similar way to precipitation, the maximum accumulated dry-spell duration (P_i) of a DSS event is defined as

$$\begin{array}{}\text{(1)}& P_i=max{\left\{\sum _{j=k}^{k+i-\mathrm{1}}{D}_j\right\}}_{k=\mathrm{1}}^{N-i+\mathrm{1}},\end{array}$$

where i is the number of accumulated events, and N is the total considered events. For each DSS event, maximum average duration Y_i at i step is

$$\begin{array}{}\text{(2)}& Y_i={\displaystyle \frac{P_i}{i}}.\end{array}$$

Therefore, the maximum average duration satisfies a scaling relationship with respect to this event number:

$$\begin{array}{}\text{(3)}& {\displaystyle \frac{Y_i}{Y_{\mathrm{1}}}}={\left({\displaystyle \frac{\mathrm{1}}{i}}\right)}^n,\end{array}$$

where Y₁ is the maximum expected dry length per year and n is the n index, which is bounded as $d\le n\le \mathrm{1}$, i.e. between the fractal dimension (d) of the spells considered and the dimension of the time series (Monjo, 2016). The parameters Y₁ and n were fitted for each DSS and averaged for each time series of grid points. Taking Eqs. (2) and (3), maximum accumulated dry-spell duration (P_i) is

$$\begin{array}{}\text{(4)}& P_i=Y_{\mathrm{1}}{i}^{\mathrm{1}-n}.\end{array}$$

2.2 Statistical analysis

Due to the low probability of the longest spells, a high maximum duration Y₁ implies a big difference in relation to the previous and subsequent durations; i.e. it implies high values for n. Therefore, a statistical link is expected between the probability distributions of Y₁ and n. In order to test this hypothesis, it suffices to set a distribution for one and a fit for the other. For example, if a distribution over Y₁ is set as $\mathrm{1}-\mathrm{1}/Y_{\mathrm{1}}$, we can find a distribution F(n) of n, such as

$$\begin{array}{}\text{(5)}& \mathrm{1}-{\displaystyle \frac{\mathrm{1}}{Y_{\mathrm{1}}}}=F\left(n\right).\end{array}$$

In particular, two parametric versions of three theoretical distributions were fitted: exponential (F1), classical Gumbel (F₂), and opposite Gumbel (F₃) distributions (Monjo and Martin-Vide, 2016):

$$\begin{array}{}\text{(6)}& {\displaystyle }& {\displaystyle }{F}_{\mathrm{1}}\left(n\right)=\mathrm{1}-\exp (-{\mathit{\alpha }}_{\mathrm{1}}n+{\mathit{\beta }}_{\mathrm{1}}),\text{(7)}& {\displaystyle }& {\displaystyle }{F}_{\mathrm{2}}\left(n\right)=\exp (-\exp (-{\mathit{\alpha }}_{\mathrm{2}}n+{\mathit{\beta }}_{\mathrm{2}}\left)\right),\text{(8)}& {\displaystyle }& {\displaystyle }{F}_{\mathrm{3}}\left(n\right)=\mathrm{1}-\exp (-\exp ({\mathit{\alpha }}_{\mathrm{3}}n+{\mathit{\beta }}_{\mathrm{3}}\left)\right).\end{array}$$

The Akaike information criterion (AIC) was applied to each fitted model using the log-likelihood function according to the equation

$$\begin{array}{}\text{(9)}& {\displaystyle }AIC=-\mathrm{2}\log \left(\widehat{L}\right)+p_{\mathrm{m}}k,\end{array}$$

where $\widehat{L}$ is the maximum value of the likelihood function for the model fitted, p_m is the number of parameters in the model, and k=2 is used for the usual AIC, or k=log (N) (with N equal to the number of observations) for the so-called BIC (Bayesian information criterion; Fig. A3).

2.3 Cantor-based exponent

Finally, the lacunarity of the Cantor set was compared with the frequency distribution of dry-spell durations for a given time series of L days. To this end, a Cantor-based time series was built using segments of zeros or gaps {G_kj} found between consecutive Cantor points (represented by segments of ones) obtained by the kth iteration given by $k=\log \left(T\right)/\log \left(\mathrm{3}\right)$, where T is the length of the binary time series considered. For example, for the first iteration, k=1, only the gap $G_{\mathrm{1}i}=T/\mathrm{3}$ is obtained; for k=2, three gaps are found, $G_{\mathrm{2}i}=\mathit{\{}T/\mathrm{9},T/\mathrm{3},T/\mathrm{9}\mathit{\}}$; for k = 3, seven gaps are found, $\mathit{\left\{}{G}_{\mathrm{3}i}\mathit{\right\}}=\mathit{\{}T/\mathrm{27},T/\mathrm{9},T/\mathrm{27},T/\mathrm{3},T/\mathrm{27},T/\mathrm{9},T/\mathrm{27}\mathit{\}}$; and so on. The set of gaps greater than 1,

$$\begin{array}{}\text{(10)}& {\mathrm{\Gamma }}_k:=\underset{i}{\mathrm{sort}}\left\{{\displaystyle \frac{G_H}{T}}:G_H>\mathrm{1}\right\},\end{array}$$

was compared with that obtained from the set of dry spells,

$$\begin{array}{}\text{(11)}& \mathrm{\Delta }:=\underset{j}{\mathrm{sort}}\left\{{\displaystyle \frac{D_j}{L}}:D_j>\mathrm{1}\right\}.\end{array}$$

The value of the iteration k was chosen as the minimum iteration when the total number of elements of Δ is less than, or equal to, the total number of elements (cardinal) of Γ_k, i.e. $\left|\mathrm{\Delta }\right|\le \left|{\mathrm{\Gamma }}_k\right|$. Finally, we defined a Cantor-based exponent C_e by the quantile–quantile map:

$$\begin{array}{}\text{(12)}& \mathrm{\Delta }={\mathit{\delta }}_{\mathit{ϵ}}\cdot {{\mathrm{\Gamma }}_k}^{C_{\mathrm{e}}}.\end{array}$$

The results of the dry-spell n index were compared with other dryness fractal measures in each grid point: the Cantor-based exponent (C_e), the Hurst exponent (H), and the Gini index (G), with all the cases estimated considering the entire time series of dry spells {D_j}. The Gini index is defined as the area under the Lorenz curve, which describes the relative accumulation of the variable D_j and its cumulative frequency (Monjo and Martin-Vide, 2016). Alternatively, the Hurst exponent measures the possible long memory in time series. Given a set {A_i} formed by T anomalies A_i of the variable (D_j) and the corresponding set {C_i} of T cumulative values C_i from A₁ to A_j, the Hurst exponent H is obtained from the relation $R/S=k_H\cdot T^H$, where k_H is a constant, S is the standard deviation of the set {A_i}, and R is the range (i.e. maximum minus minimum value) of the set {C_i} (Mandelbrot, 1985; Feder, 1988).

2.4 Data considered

The data used in this study were obtained from the full global gridded daily Multi-Source Weighted-Ensemble Precipitation (MSWEP) dataset (Beck et al., 2017). The MSWEP combines gauge-, satellite-, and reanalysis-based data to provide reliable precipitation estimates. The study period comprises the years 1979–2016 (total of 45 165 d), and a spatial resolution of 0.5^∘, with a total of 259 197 grid points (Fig. A1).

3 Results

3.1 Drought patterns detected

By analysing dry-spell spells (DSSs), the first overview of the spatial distribution of the DSS n index is given by seven quasi-latitudinal bands (Fig. 1): three low-value bands in the equatorial zone and at medium latitudes in both hemispheres and four high-value bands in the two tropical areas and in the two polar areas. These bands generally correspond to the large climatic areas of the world. Indeed, there is a statistically significant relationship between annual dry days and the n index (Fig. A1).

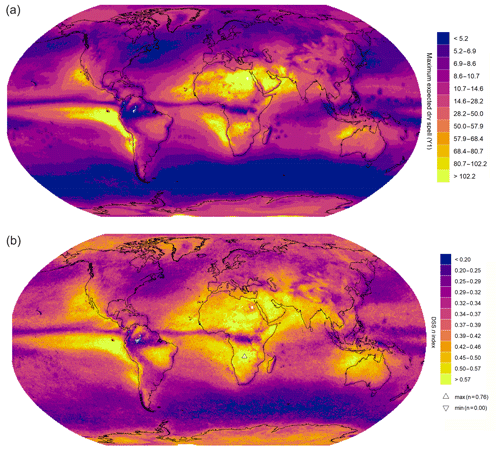
Figure 1 Spatial distribution of regularity of the lacunarity, averaging for all DSS events: (a) maximum expected dry spell (Y₁) and (b) DSS n index.

More specifically, rainforests like those in the Amazon, the Congo, or southeastern Asia present values of n<0.3. This is consistent with the low values also found for other rainforest zones such as those in Madagascar, Central America, and South America. This is due to the high degree of persistence of very short dry spells, alternating with very frequent wet days. Low values are also provided by the domain regions due to the action of the polar jet streams in both hemispheres. This is the case of the zonal flux in the Southern Ocean and the eastern fringes of North America and Asia.

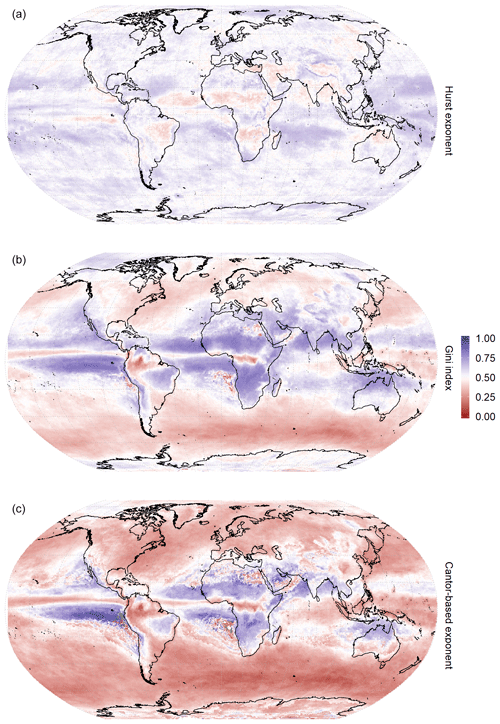
High values of the index (n>0.4) are presented in the tropical and subtropical regions due to the effect of the subtropical anticyclones, particularly in the deserts. The savannah regions show the highest values of n, which involve a long dry spell followed by shorter dry events. The polar regions score a secondary maximum of n due to the usually long but irregular dry events. Similar spatial results are found if G and C_e are used (Fig. 2), while the Hurst exponent displays noisier patterns around the world, very close to 0.5, as described by other studies for Europe (Martínez et al., 2007; Lana et al., 2010). Most of the cases show values n<0.5; similarly, approximately 80 % of the G values are lower than 0.5. Both results indicate the existence of a noteworthy degree of homogeneity in the distribution of the dry spells along the time series. In fact, the Hurst exponent is close to 0.5 (i.e. the associated fractal dimension could be 1.5), which can be interpreted as an equilibrium between positive and negative autocorrelations.

Figure 2 Spatial distribution of other fractal measures applied to dry spells: (a) Hurst exponent, (b) Gini index, and (c) Cantor-based exponent.

3.2 Drought classification

Three main sets can be identified according to the predominance of low (L), medium (M), or high (H) values of the DSS n index: Type S when n<0.3, Type M if n is within the interval (0.3, 0.4), and Type L for n>0.4. For the three main types, it is advisable to distinguish between the alternation with longer (ℓ) or shorter (s) wet events, for example, considering the threshold of three consecutive wet days (Fig. A1). Therefore, six large drought types can be defined based upon the combination of both criteria (Fig. 3):

• Type Lℓ. This is the occurrence of very short dry spells alternating with longer wet spells. Tropical examples include the main rainforest cores of the world (within the Amazon, the Congo, and southeastern Asia, among others), and subpolar examples include the Southern Ocean and some regions of the North Atlantic and North Pacific oceans.

• Type Ls. This is the occurrence of very short dry spells alternating with short wet spells. Examples include northeastern America and northeastern Asia, especially Japan.

• Type Mℓ. These are median dry spells alternating with longer wet spells. Examples include the Arctic Ocean and northern Asia.

• Type Ms. These are median dry spells alternating with shorter wet spells. Examples include the central area of North America and the temperate regions of the Atlantic and Pacific Oceans.

• Type Hℓ. This is the occurrence of very long dry spells alternating with long wet events. Examples include the tropical savannah regions of Africa, Mexico, central Brazil, India (monsoon climate), southern China, and northern Australia.

• Type Hs. This is the occurrence of very long dry spells alternating with short wet events. Examples include all the desert regions around the world, including the eastern fringe of the tropical oceanic areas.

Figure 3 Climatic classification of meteorological droughts around the world: regions with low (L), medium (M), or high (H) values of the DSS n index, alternating with longer (ℓ) or shorter (s) wet events.

3.3 Drought lacunarity

Since the total (1-D) length of the Cantor set is zero, the total length of the complementary gaps is equal to 1. That is, following the analogy between the drought duration and the Cantor set lacunarity, the total duration of a dry-spell series approaches 1 when the size of the measurement box is accurate. For instance, one can find dry days in a wet month, and on rainy days, there can be several hours with no rain. If a ground point is used for measurement, the duration of a raindrop hitting the ground (from leading surface to trailing surface) tends towards zero, and thus the dry pauses are distributed paradoxically throughout an entire rainy day.

According to this idea, the dimension of the drought duration is practically 1 (the length of the time series), and the box-counting dimension therefore makes more sense for measuring rainfall duration than for estimating drought duration. However, the lacunarity of the drought can be analysed by means of other measures, such as the Gini index (G) and the Cantor-based exponent (C_e), both of these related to the frequency of dry-spell durations. In particular, the Cantor-based exponent indicates how likely it is to find longer dry spells over time. For instance, if C_e∼0, all dry spells will present similar lengths and therefore the standard deviation will be constant (i.e. extreme values are normally distributed). However, if C_e∼1, the distribution of lengths is similar to the Cantor lacunarity, and the standard deviation will therefore increase over time. In this case, extreme dry spells show a linear increase for longer time series (in the same way that the maximum Cantor gap is set at 1∕3 of the total length), and the Gini index also tends to approach 1. Indeed, the correlation between the G and C_e is R²=0.86 (p value <0.0001) and the approximation C_e=G only provides an error of 10 %, thus reinforcing the lacunar interpretation of the dryness.

4 Discussion

The DSS n index provides information on the structure of drought lacunarity, in particular measuring the probability of regularity (if n∼0) or irregularity (if n∼1). Regular values of dry spells indicate that similar dry-spell lengths are usually consecutive. Accordingly, irregular values imply that long dry spells are followed by much shorter dry sequences. It should be kept in mind a high degree of irregularity is correlated with the longest dry spells (Fig. A3).

In short, the time patterns of the dryness of a climate can be characterised in a simple manner by means of the n index. This indicator represents a synthetic DSS, computed by averaging all the DSS events of a considered time series. In each DSS, a relative distribution can be observed of consecutive dry spells and the maximum dry-spell duration. For example, the highest values of the DSS n index (observed in parts of Africa) imply a high accumulation of dry-spell durations with a low number of events considered, whereas the lowest values of the DSS n index (found in the northwestern Amazon) point to a constant and linear accumulation of dry spells presenting the same (short) duration (Fig. A4). The DSS n index therefore provides information on the relative distribution of dry spells, on the longest duration, and on the total accumulated duration. Indeed, the start and end of a synthetic DSS event can be established by the number i of dry-spell events so that the averaged maximum duration Y_i is a particular threshold (e.g. 1 d, which is defined as the dry threshold of a DSS event). This idea enables the concept of a DSS event to be employed as an alternative definition of meteorological drought, with diffuse borders that, paradoxically, are well defined by the n index. For instance, if Y_i=0 is considered to be drought borders, the total duration of the dryness coincides with the total length of a time series (as the length of the supplementary gaps of the Cantor set). In this case, the difference between one drought and another is given by the decay rate of the maximum dry spell (well measured by the n index).

As in (fractal) wet spells, the behaviour of dryness is self-similar on all timescales – that is to say, dry spells can be used at the daily, monthly, yearly resolution, etc., considering specific dryness thresholds. This is guaranteed by the goodness of fit of the n index model (p value <0.0001). The proposed mathematical definition is complementary to the previous ideas on the persistence of dryness, for example, according to upper-order Markov chains (Lana et al., 2018). Indeed, the order of chains depends on the alternation and frequency of short and long dry spells, as with the rest of the measures (Gini index, Hurst exponent, n index, etc.).

Finally, the main limitation in this study is the possible errors derived from the used precipitation dataset. However, the source errors are generally smaller for the breaks between dry and wet spells because they are not influenced by the absolute precipitation amount.

5 Code and data availability

The datasets from Figs. 1–3 and Fig. A1 can be accessed through Monjo et al. (2019) (https://doi.org/10.5281/zenodo.3247041). The used software code (R programming language) with a point example can be accessed through Monjo et al. (2019) at GitHub: https://github.com/robertmonjo/drought.

6 Conclusions

As a principal conclusion, the study demonstrates that drought lacunarity can be analysed with the use of self-similarity features obtained from the DSS n index. This measure is useful for characterising the temporal and spatial patterns of drought, which are consistent with the climatic features established worldwide. For instance, localities presenting very frequent wet spells alternating with short dry spells provide low values of the DSS n index (this is the case, for example, in the Amazon, the Congo, and other rainforests). This results from an accumulation of isolated short dry spells, all presenting the same duration. Additionally, places with longer dry spells (such as deserts) scored higher values on the DSS n index. This result is logical because the n index is strongly correlated with the maximum and average lengths of dry spells as well as with the Gini index.

Consequently, we arrived at a second conclusion: the methodology developed can be used to classify typologies of meteorological drought. Indeed, six climate types have been proposed: these result from the combination of three classes of DSS n index values (Type L when n<0.3, Type H for n>0.4, and Type M otherwise) and two sub-classes based on the alternation with longer (ℓ) or shorter (s) wet events. This classification could be useful with regard to monitoring possible changes in drought patterns around the world within the context of climate change (Monjo et al., 2016; Craine et al., 2013; Madakumbura et al., 2019). The third and most important outcome refers to the fact that consideration of dryness lacunarity provides a better understanding of drought duration and helps to predict when droughts start and finish. Further works may use other dataset at a global or regional scale (with more spatial resolution) to analyse past and future climate change (e.g. by using CMIP6 climate models). Moreover, future studies may focus on designing specific indicators to monitor hydrological and agricultural droughts, especially involving datasets on river discharges, soil moisture, water stress, or related damage. In particular, the value of the DSS n index is related to the effective duration (according to borders determined by a threshold of the minimum expected dry spell). Indeed, the best analogy with regard to understanding the features of the DSS is Cantor lacunarity; i.e. total dry spells are almost equal to the length of the entire series (in the same manner that the total length of Cantor voids is equal to 1). The methodology presented here provides a set of potentialities: from analysing the change of drought regimes to feeding indicators for monitoring impacts on agricultural or hydrological droughts, with the possibility of using data with a higher spatial resolution.

Appendix A

Note that the mean dry spell (MDS) and the mean wet spell (MWS) are geographically distributed, with a strong correspondence between the high (low) values of the one and the low (high) values of the other. A general zonal pattern is observed, albeit with a clear dissymmetry between the western facades of the continents and the eastern oceans, in tropical–subtropical latitudes, with high values of the MDS (low values of the MWS), and their responses, with low (high) values. The highest values of the MDS are concentrated in the tropical–subtropical zones, especially in the Sahara and its continuation in the Arabian Desert, in the Persian Gulf and the waters of the Indian waters of the Indian Ocean, in lower California, in northern Chile, on the coast of Peru and its waters, in the Atlantic Ocean off the coast of Namibia, and towards the west–northwest of Australia (bordering with Antarctica). The most similar values between both indices, specifically with high values in both, are observed in the Asia-Pacific region (monzonic region), reflecting the division of the year into two halves, the rainy summer, with long rains, and the dry winter, with an absence of precipitation for many days in a row. This pattern can be detected in other areas presenting a humid–dry tropical climate, such as the southernmost area of the Sahel, northeastern Brazil, an area in Africa (south of the Equator), and northern Australia. The SW–NE diagonals of mid-latitudes with decreasing values of the MDS in the Atlantic and the Pacific are clearly appreciated, according to the westerlies and the track of the low-pressure systems.

For instance, let $D=(\mathrm{2},\mathrm{1},\mathrm{10},\mathrm{4},\mathrm{8},\mathrm{10},\mathrm{20},\mathrm{1},\mathrm{2})$ be a time series of consecutive dry spells. A DSS event is built around the minimum value (D₀=1) as (10, 4, 8, 10, 20). Subsequently, maximum accumulated dry durations are $P_i=(\mathrm{20},\mathrm{30},\mathrm{38},\mathrm{42},\mathrm{52})$, and the maximum averaged dry durations are $Y_i=(\mathrm{20},\mathrm{15},\mathrm{12.7},\mathrm{10.5},\mathrm{10.4})$, which can be fitted over the number of events (i) according to Eq. (3).

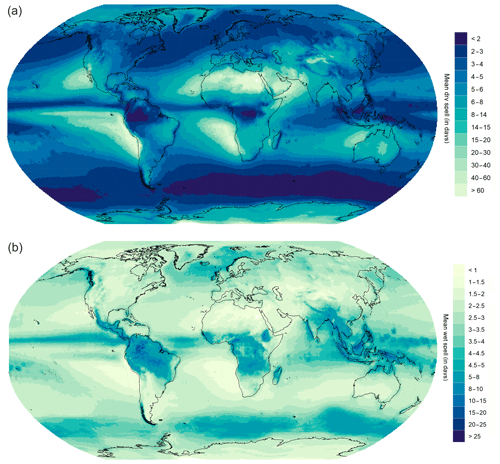
Figure A1 Spatial distribution of mean dry spell (a) and mean wet spell (b) at a spatial resolution of $\mathrm{0.5}{}^{\circ }\times \mathrm{0.5}{}^{\circ }$ according to the MSWEP dataset (1979–2016).

Figure A2 Method for defining DSS events and their corresponding n index.

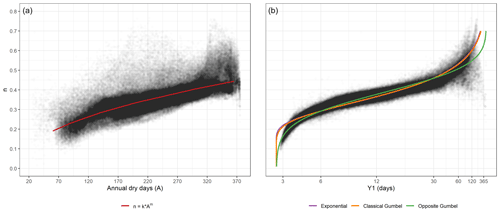
Figure A3 Statistical relationship between (a) annual dry days (A) and the DSS n index and (b) maximum expected dry spell (Y₁) and the DSS n index.

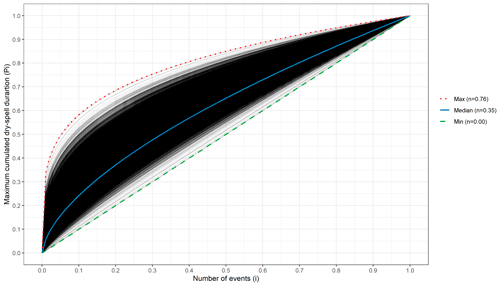
Figure A4 Fitted curves of DSS events (Eq. 4), according to the maximum accumulated dry-spell duration (P_i) over the number of events considered (i), both normalised according to the total values.

The fitted parameters for the first curve are k=0.02811(3) and m=0.4677(8) (R²=0.67, p value <0.0001). In the second panel, the fitted curves are exponential (α₁=0.997(3), ${\mathit{\beta }}_{\mathrm{1}}=-\mathrm{9.543}\left(\mathrm{7}\right)$, AIC ≈ BIC $=\mathrm{1.4}\times {\mathrm{10}}^{\mathrm{6}}$, R²=0.91, p value <0.0001), Gumbel (α₂=1.225(3), ${\mathit{\beta }}_{\mathrm{2}}=-\mathrm{10.01}\left(\mathrm{1}\right)$, AIC ≈ BIC $=-\mathrm{1.2}\times {\mathrm{10}}^{\mathrm{6}}$, R²=0.88, p value <0.0001), and opposite Gumbel (α₃=3.829(2) and ${\mathit{\beta }}_{\mathrm{3}}=-\mathrm{0.5347}\left(\mathrm{9}\right)$, AIC $=-\mathrm{1.1}\times {\mathrm{10}}^{\mathrm{6}}$, R²=0.87, p value <0.0001), according to the Eqs. (6)–(8).

Note that the minimum DSS n index corresponds to the Amazon, where almost every DSS event lasts for only 1 d, and the accumulation of dry spells (Y_i) is therefore very regular. Furthermore, the maximum n index (close to the Zambezi River) represents an average DSS event with a maximum dry spell of 33 % of the total accumulated dry-spell length (most of the entire time series) and successive dry spells with shorter durations (as in the Cantor gaps).