the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Sea-level fingerprints emergent from GRACE mission data
Surendra Adhikari
Erik R. Ivins
Thomas Frederikse
Felix W. Landerer
Lambert Caron
The Gravity Recovery and Climate Experiment (GRACE) mission data have an important, if not revolutionary, impact on how scientists quantify the water transport on the Earth's surface. The transport phenomena include land hydrology, physical oceanography, atmospheric moisture flux, and global cryospheric mass balance. The mass transport observed by the satellite system also includes solid Earth motions caused by, for example, great subduction zone earthquakes and glacial isostatic adjustment (GIA) processes. When coupled with altimetry, these space gravimetry data provide a powerful framework for studying climate-related changes on decadal timescales, such as ice mass loss and sea-level rise. As the changes in the latter are significant over the past two decades, there is a concomitant self-attraction and loading phenomenon generating ancillary changes in gravity, sea surface, and solid Earth deformation. These generate a finite signal in GRACE and ocean altimetry, and it may often be desirable to isolate and remove them for the purpose of understanding, for example, ocean circulation changes and post-seismic viscoelastic mantle flow, or GIA, occurring beneath the seafloor. Here we perform a systematic calculation of sea-level fingerprints of on-land water mass changes using monthly Release-06 GRACE Level-2 Stokes coefficients for the span April 2002 to August 2016, which result in a set of solutions for the time-varying geoid, sea-surface height, and vertical bedrock motion. We provide both spherical harmonic coefficients and spatial maps of these global field variables and uncertainties therein (https://doi.org/10.7910/DVN/8UC8IR; Adhikari et al., 2019). Solutions are provided for three official GRACE data processing centers, namely the University of Texas Austin's Center for Space Research (CSR), GeoForschungsZentrum Potsdam (GFZ), and Jet Propulsion Laboratory (JPL), with and without rotational feedback included and in both the center-of-mass and center-of-figure reference frames. These data may be applied for either study of the fields themselves or as fundamental filter components for the analysis of ocean-circulation- and earthquake-related fields or for improving ocean tide models.
- Article
(4732 KB) - Full-text XML
- BibTeX
- EndNote
© 2019 California Institute of Technology. Government sponsorship acknowledged.
Geodesists have long understood that the ocean mean sea surface follows the shape of the Earth's geoid (Rapp, 1983) and that changes in on-land water storage are a source of time-varying gravity (Lambert and Beaumont, 1977). The fundamental relationship of changes in land ice and water, solid Earth, and sea-surface height is essential to the study of past and present relative sea level (e.g., Peltier, 1982; Clark et al., 2002; Tamisiea, 2011). Our recent gain in confidence for monitoring the geographic locations and amplitudes of both seasonal and supra-seasonal changes in global glacier and ice sheet mass, dating to the beginning of the radar interferometry and altimetry era of the early 1990s (e.g., Rignot et al., 2011; Shepherd et al., 2018), strengthens our ability to effectively harness this information to construct informative models about global sea-level variability associated with a self-attraction and loading phenomenon (Spada and Galassi, 2016; Larour et al., 2017; Mitrovica et al., 2018). The mathematical formalism relating changes in gravitational, rotational, and solid Earth deformation responses to land ice and hydrological mass change has now niched itself into contemporary studies of sea-level change: the prediction of “sea-level fingerprints”. Sea-level fingerprints are a consequence of the fact that the water elements being transported laterally between land and oceans carry mass, gravitational attraction, and the ability to change the radial stress at the solid Earth surface. These are characterized, for example, as changes in relative sea level encircling areas of intense ice mass loss such as Patagonia, coastal Alaska, the Amundsen Sea sector of West Antarctica, and the Greenland Ice Sheet (e.g., Mitrovica et al., 2001; Tamisiea et al., 2014; Riva et al., 2010; Adhikari and Ivins, 2016).
To date, space gravimetric measurements using Gravity Recovery and Climate Experiment (GRACE) monthly gravity fields and the subpolar ocean altimetry measurements from TOPEX/Poseidon and Jason each have multiple geophysical signals and respective noise floors that are generally high enough that clear detection of these contemporary land-mass-driven fingerprints in the oceans has remained elusive. However, it is believed that these signals will eventually emerge in these data systems. Such a belief springs, in part, from the fact that amplitudes of internal ocean variability in intra- and interannual mass that GRACE observes are relatively mute in comparison to on-land hydrology, two-way land-to-ocean transport, and secular trends in land ice changes (Chambers, 2006; Chambers and Willis, 2008; Watkins et al., 2015; Wiese et al., 2016; Save et al., 2016). In fact, Hsu and Velicogna (2017) have used ocean-bottom pressure data, in conjunction with space geodetic data, to claim that fingerprints associated with decadal-scale on-land mass changes are detected. Furthermore, Davis and Vinogradova (2017) have shown that the fingerprints of Greenland ice mass loss have had measurable influences on tide gauge records along the eastern coast of the US since the mid-1990s. Galassi and Spada (2017) have noted that the influence of a land-mass-induced fingerprint may be reflected in tide gauge records of relative sea level at the northern Antarctic Peninsula, as there is a distinct change in trend at about the year 2000 CE, possibly reflecting increased regional ice mass loss. Each of these observations might be considered both intriguing and preliminary in terms of providing the community with unambiguous detection of sea-level fingerprints.
The effects of the fingerprints are nonetheless important to disentangle from many geophysical and ocean circulation models and dataset. New insights into the regional and global sea-level budgets are sought through explicitly combining ocean altimetry with the space gravimetry information, and a key part of this combination is to account for the details of sea-level fingerprints (e.g., Rietbroek et al., 2012; Frederikse et al., 2018). Consideration of land-ice- and water-driven fingerprints is also necessary when using geodetic data to search for glacial isostatic adjustment (GIA) signals residing at or beneath the seafloor (e.g., Simon et al., 2018) or examining ice loss on land when ocean water surrounds the region, such as in Graham Land of the Antarctic Peninsula (Ivins et al., 2011; Sterenborg et al., 2013). Future applications of sea-level fingerprints in geophysical geodesy should include the study of great earthquakes (Mw≥8.0) at subduction zones (Han et al., 2016) and at ocean rifts beneath the open ocean (Han et al., 2015) or adjacent to the Antarctic Ice Sheet (King and Santamaría-Gómez, 2016).
This paper describes a dataset of monthly changes in relative sea level, geoid height, and vertical bedrock motion induced by mass redistribution from land to ocean. These are derived from the Release-06 GRACE Level-2 monthly Stokes coefficients for the period April 2002 to August 2016. The GRACE mission data have been instrumental to the study of the Earth's climate system (Tapley et al., 2019) and have helped us resolve numerous long-standing questions in oceanography, hydrology, cryosphere, and geodesy. The GRACE gravity solutions are now employed for providing new insights into changes in ocean circulation (Johnson and Chambers, 2013; Landerer et al., 2015; Saynisch et al., 2015; Mazloff and Böning, 2016). The terrestrial water storage is now rigorously quantified for continents (Rodell et al., 2015; Hirschi and Seneviratne, 2017) as is the global cryospheric mass balance (Velicogna, 2009; Jacob et al., 2012; Ivins et al., 2013; Luthcke et al., 2013; Schrama et al., 2014). Land mass change and its exchange with the global oceans, in fact, makes it possible to successfully reconstruct subtle changes in the position of Earth's spin axis on interannual timescales (Adhikari and Ivins, 2016), thus providing a confidence in the robustness of GRACE-based estimates of global surface mass transport.
Relative sea level is defined as the height of the ocean water column bounded by two surfaces: solid Earth surface and sea surface. Change in relative sea level, ΔS, at a geographical location described by colatitude and longitude (θ,ϕ) over the time interval Δt may be expressed as follows:
where ΔN and ΔU are corresponding changes in sea-surface height and bedrock elevation, respectively. Both of these variables are usually expressed relative to the reference ellipsoid, which in turn is defined relative to either the center-of-mass (CM) of the total Earth system or the center-of-figure (CF) of the solid Earth surface. Tide gauges provide direct measurements of ΔS, whereas satellite altimetry measures ΔN in the CM reference frame.
Mass redistributed on Earth's surface provides a direct perturbation to the Earth's gravitational and rotational potentials, causing a corresponding perturbation in the geoid height. Since the geoid height on a realistic Earth does not necessarily have to coincide with the sea-surface height, we write
where ΔΦ is the net perturbation in Earth's surface potential, ΔC is a spatial invariant that explains the discrepancy between the sea-surface height and geoid height (Tamisiea, 2011), measured with respect to the same reference ellipsoid, and g is the mean gravitational acceleration at Earth's surface. As will be further discussed in Sect. 3, ΔC is essential to conserve mass. Space-based gravity missions, such as GRACE and GRACE Follow-On (GRACE-FO), provide direct measurements of the non-rotational part of ΔΦ (to be defined explicitly in Sect. 3) in the CM frame; the satellite system cannot measure the rotational part of ΔΦ because it retrieves data in an inertial reference frame.
In geodetic applications, global field variables are typically expanded in a spherical harmonic (SH) domain. Most of the GRACE data processing centers – including the University of Texas Austin's Center for Space Research (CSR), GeoForschungsZentrum Potsdam (GFZ), and Jet Propulsion Laboratory (JPL) – provide monthly solutions for normalized SH coefficients of the gravitational potential termed “Stokes coefficients”. Stokes coefficient anomalies – the values that deviate from the mean (static) field – can be used to readily retrieve changes in on-land ice and water storage or ocean bottom pressure. The goal of this paper is to provide Stokes coefficient anomalies (i.e., SH coefficients of ΔΦ minus rotational centrifugal potential) associated with the sea-level fingerprint of monthly changes in on-land ice and water storage, which are derived from CSR, GFZ, and JPL GRACE Stokes coefficients themselves. As we shall further clarify below, we provide these new fingerprint coefficients and their corresponding spatial maps computed in both CM and CF reference frames, with and without rotational feedback included. We also provide solutions for change in relative sea level ΔS and bedrock elevation ΔU. Corresponding solutions for sea-surface height, ΔN, may be retrieved using Eq. (1). For brevity, we hereafter drop the Δ symbol and assume that variables imply “change” in respective fields – not the absolute fields – implicitly.
Here we briefly summarize the fundamental concept and a numerical technique of solving the so-called “sea-level equation”. Much of the background and supporting materials may be found, for example, in Farrell and Clark (1976), Mitrovica and Peltier (1991), Adhikari et al. (2016), and Spada (2017). Let be the global, mass-conserving load function so that
where is the on-land change in water equivalent height over the time period t, and is the corresponding change in relative sea level on the oceanic domain 𝒪(θ,ϕ). By definition, 𝒪=1 for the oceans and 0 otherwise. For ease of discussion, we write so that defines the model “forcing” function.
The net change in on-land (water) mass directly affects the relative sea level, hence conserving mass on a global scale. Such a redistribution of mass on Earth's surface perturbs its gravitational and rotational potentials and further redistributes the ocean mass. The net result of these perturbations is the sea-level fingerprint: a unique spatial pattern of relative sea level that is consistent with fundamental physical features of a realistic Earth. For a self-gravitating elastically compressible rotating Earth, we compute the sea-level fingerprint by satisfying the following sea-level equation:
The physical interpretation of the right-hand side terms is as follows:
-
The barystatic term, E(t), directly follows from the mass conservation principle. This spatial invariant describes S that would be resulted in by distributing the net change in land water storage uniformly over the oceans.
-
Changes in the Earth's surface potential, , and the solid Earth surface, , may be partitioned as follows:
where Φg and Ug are the respective signals associated with the perturbation in gravitational potential. We may compute Φg and Ug by convolving L (Eq. 3) with the respective Green's functions. Similarly, Φr and Ur are associated with the perturbation in rotational potential. The change in Earth orientation driven by shift in the inertia tensor causes both solid Earth deformation and sea-level change (Lambeck, 1980). The net effects of the change in orientation of Earth's spin axis thus provide a rotational feedback (e.g., Milne and Mitrovica, 1998). We may compute Φr and Ur based on the perturbation in Earth's inertia tensor due to the global surface mass redistribution described by L (Eq. 3). We define all of the terms appearing in Eqs. (4) and (5) explicitly in Appendix A.
-
The last term in Eq. (4) represents the ocean-averaged value of . This spatial invariant is essential to ensure that the global mean relative sea-level change is the same as the barystatic term.
To solve for the sea-level fingerprint in a conventional SH domain (e.g., Mitrovica and Peltier, 1991) and isolate useful SH coefficients noted in Sect. 2, we express Eq. (4), using Eq. (5), in the following form:
where , , , , and . By default, we account for the rotational feedback, which when excluded, Eq. (6) takes a reduced form with Y=0, Q=0, and . We now multiply both sides of Eq. (6) by the ocean function, 𝒪, to get the following:
where , , and so on. In the employed spectral methods (Appendix B), we find it more straightforward to solve Eq. (7) rather than Eq. (6). Since all of the right-hand side terms appearing in Eq. (7) depend on itself (see Eqs. 3 and 4 and Appendix A), we solve the equation recursively until the desired solution convergence is achieved (see Appendix B5). We consider the barystatic sea level (Eq. A1) as the starting solution; i.e. , where . Once Eq. (7) is solved for , all of the terms appearing in Eq. (6) may be retrieved easily.
We expand all of the terms appearing in Eqs. (6) and (7) in the SH domain (as in Eq. B1). Inserting these SH expansions into Eq. (7) and equating the corresponding (degree l, order m) SH coefficients, we find the following for any rth recursion:
where is the recursion counter, and rmax is the value of r for which the desired convergence is attained. Note that dependence of right-hand side terms on itself is explicitly stated. For r=1, we set . Since does not depend on , it does not evolve during the recursion. We define (Eq. B17) and all of the other hatted coefficients appearing above (Eq. B18 and so on) in Appendix B. The hatted coefficients depend on corresponding non-hatted coefficients, which are explicitly defined in Eqs. (B20)–(B23) and (B25).
Once we obtain the final solution for (after iteration r=rmax), denoted for simplicity by , final solutions for all of the non-hatted (degree p, order q) coefficients are obtained as well. These non-hatted coefficients automatically satisfy the sea-level equation itself (Eq. 6) in the SH domain; i.e.,
Note that all of the SH coefficients appearing above are only a function of time t. With final solutions achieved for all of the terms appearing in Eq. (9), SH coefficients of geoid height change for a self-gravitating Earth are given by Xpq(t) and those for a self-gravitating rotating Earth by [Xpq(t)+Ypq(t)]. Similarly, SH coefficients of bedrock elevation change are given by −Ppq(t) for a self-gravitating Earth and by for a self-gravitating rotating Earth.
Here we give a brief summary of the steps undertaken to develop sea-level fingerprints and complementary data products. First, we note that the GRACE processing centers, including CSR, GFZ, and JPL, have a variety of methods employed to reduce noise, but the system has an inherent resolution limit of about 300 to 400 km in radius at the Earth's surface. Hence, the Stokes coefficients for the potential field provided by the official centers are truncated at a varying degree and order, from 60 to 96. We employ a truncation at degree and order 60, as many months may be much noisier than others.
We use GRACE Level-2 Release-06 data products provided by all three premier (and official) data processing centers (available at ftp://podaac.jpl.nasa.gov/allData/grace/L2/, last access: 7 May 2019) that are available for the spans April 2002 through August 2016 (CSR and JPL) and January 2003 through November 2014 (GFZ). The Release-06 GSM files represent the total gravity variability due to land surface hydrology, cryospheric changes, episodic seismogenic processes, and GIA. We assume that all mass transport information is contained within the post-processed GSM files in which background models for the mass changes in atmosphere and oceans having periodicities shorter than 1 month are removed (Dobslaw et al., 2017). GSM datasets are also corrected for solid Earth and ocean tides by the processing centers (see Stammer et al., 2014; Bettadpur, 2018). We also assume continuous transfer of net mass to and from the oceans takes place on all timescales. This includes a trend that supplies the mass term of sea-level rise. To do this correctly, we derive degree 1 coefficients from JPL Release-06 data products following the methods of Swenson et al. (2008). We replace degree 2 order 0 coefficients by those derived from satellite laser ranging analysis (Cheng et al., 2011) that are compatible with Release-06 data products (available at ftp://podaac.jpl.nasa.gov/allData/grace/docs/TN-11_C20_SLR.txt, last access: 7 May 2019). The physical origins motivating this replacement are well known: there is far greater sensitivity to changes in degree 2 order 0 coefficients that can be retrieved from higher orbiting satellites tracked by terrestrial laser stations than for GRACE (Cheng and Ries, 2017). We apply GIA correction coefficient by coefficient using the expected values from a Bayesian analysis (Caron et al., 2018), available at https://vesl.jpl.nasa.gov/solid-earth/gia/ (last access: 7 May 2019). Finally, for all coefficients, we remove corresponding 11-year (January 2003–December 2013) mean values to retrieve Strokes coefficient anomalies.
By combining GSM Stokes coefficient anomalies with GIA and low-degree coefficients as noted above, we may derive corresponding coefficients for land water storage anomalies, Hlm(t), as follows (Wahr et al., 1998):
where ρw is the water density, ρe is the Earth's mean density, are the load Love numbers of degree l, a is the Earth's mean surface radius, r is the Gaussian smoothing window, and and are the GSM and GIA Stokes coefficient anomalies, respectively. The term enclosed by braces is the Gaussian smoothing filter. We consider r=300 km to comply with the so-called gain factors that are used to restore the attenuated signals (detailed below). An asterisk associated with GSM coefficients is meant to imply that these solutions are corrected for more accurate low-degree Stokes coefficients as noted above.
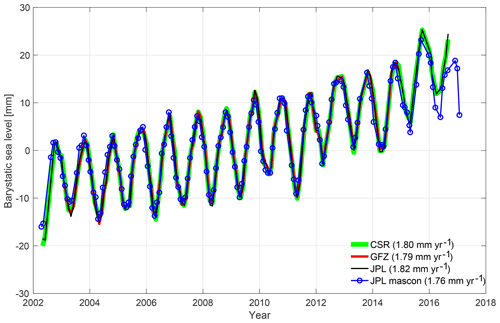
Figure 1Barystatic sea-level time series. Our estimates of trends and seasonal amplitudes for all three data centers are compared to JPL mascon solutions (Watkins et al., 2015). Results are plotted relative to the time means over the period January 2003 through December 2013. Trend values are provided for the period January 2005 through December 2015, except for GFZ solutions (January 2005 to December 2013), for a comparison to the sum of individual mass components (during January 2005 to December 2016) listed in Table 13 of the WCRP (2018) report: 1.65±0.23 mm yr−1. As an additional point of comparison, Dieng et al. (2015) find GRACE-determined mass changes for the barystatic sea-level trend at 2.04±0.08 mm yr−1 for January 2005–December 2013 from the mean of CSR, GFZ, and JPL Level-2 Release-05 spherical harmonic solutions.
Monthly land water storage fields, , may be generated by assembling the coefficients (Eq. 10) in an SH domain, as in Eq. (B1). Gaussian smoothing aimed at removing the data noise also attenuates the signals. An appropriate scaling of the fields is therefore essential. For the ice sheet and peripheral glaciers in Greenland, three non-overlapping sub-domains of Antarctica, and 15 regions of global glaciers and ice caps, we compare our estimates of average rate of regional mass change during February 2003 through June 2013 with those computed by Schrama et al. (2014) and derive the scaling factors – unique for CSR, GFZ, and JPL data products – for each of these 19 cryospheric domains. As for the non-cryospheric continental domains, Landerer and Swenson (2012) analyzed monthly land water storage signals obtained from the GRACE observations and the Noah land surface model, simulated within the Global Land Data Assimilation System (GLDAS-Noah), and derived global gridded gain factors. We combine these factors to scale for the entire continents. Our estimates of barystatic time series are comparable to, for example, JPL mascon solutions for both trends and seasonal amplitudes (Fig. 1).
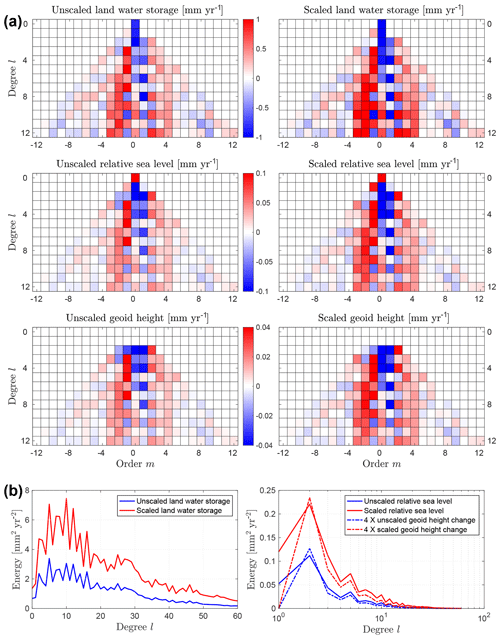
Figure 2Effects of scaling on the select spherical harmonic coefficients. (a) Scaling effects on the average rate of change in land water storage, relative sea level and geoid height, during April 2002 through March 2016. These solutions are based on JPL Stokes coefficients and are computed in the CM reference frame with the rotational feedback included. (b) Distribution of energy, computed for a given degree l as a sum of the squares of corresponding orders m, for unscaled and scaled solutions. Note the log scale on the x axis of the right panel. Unlike the geoid height change, the relative sea-level change has nonzero energy at l=0 with magnitudes of 1.16 and 2.37 mm2 yr−2 for unscaled and scaled solutions, respectively. Also note that solutions for geoid height change employ a different scale (factor of 4) for appropriate visualization.
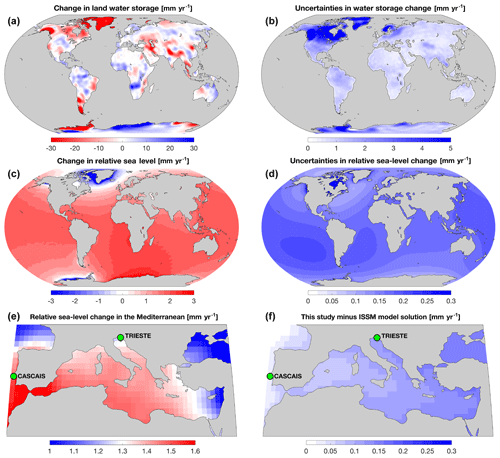
Figure 3Land load function, sea-level fingerprint, and uncertainties therein. Average rate of water equivalent height change in land water storage (a, b) and associated change in relative sea level (c, d) for the period April 2002 to March 2016 are shown with their corresponding 1σ uncertainties. Maps for sea-level fingerprint and uncertainty are produced by assembling the corresponding spherical harmonic coefficients provided with this article. These solutions are based on JPL Stokes coefficients and are computed in the CM reference frame with the rotational feedback included. A zoomed-in map of the Mediterranean Sea (e) is meant to highlight the local variability in sea-level fingerprint. The fingerprint-predicted trends for tide gauges at TRIESTE (1.26±0.18 mm yr−1) and CASCAIS (1.50±0.17 mm yr−1) reflect differences that are comparable to those associated with interdecadal atmospheric pressure trends (0.2±0.2 mm yr−1) and the GIA-related fingerprint (≈0.2 mm yr−1) (see Piecuch et al., 2016, and Stocchi and Spada, 2009, respectively). This illustrates one example of the importance of contemporary sea-level fingerprints for tide gauge data analysis and interpretation. Panel (f) is meant to show that our solutions are comparable to those obtained from a well-validated and higher-resolution ISSM sea-level solver (Adhikari et al., 2016); note that the solution discrepancy is within the 1σ uncertainties (compare with panel d).
A detailed description of scaling may be found in Adhikari and Ivins (2016), who used the same recipe to post-process the CSR Release-05 GRACE Level-2 Stokes coefficients for robust reconstruction of interannual variability in position of Earth's spin axis. This gives us extraordinary confidence that the procedure for generating land water storage fields and corresponding fingerprints are not only sound but highly robust at long wavelengths. The effects of scaling on SH coefficients of select fields are shown in Fig. 2. Our model solutions are also robust. For example, our estimates of relative sea-level change (Fig. 3), vertical bedrock motion (not shown), and geoid height change (not shown) are consistent with the respective solutions computed using a well-validated sea-level solver (Adhikari et al., 2016) that operates on an unstructured global mesh of the Ice and Sea-level System Model (ISSM; https://issm.jpl.nasa.gov/, last access: 7 May 2019). We find that GFZ solutions are slightly different from CSR and JPL solutions (Fig. 4), although the difference in sea-level fingerprints is generally within 1σ uncertainties (compare Figs. 3d and 4d). We show the origin of discrepancies by plotting the degree variance spectrum.
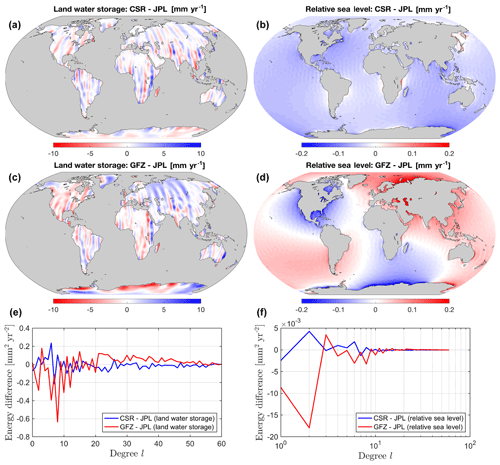
Figure 4Comparison of data centers for select fields. JPL solutions are subtracted from CSR and GFZ solutions for trend in land water storage change (a, c) and relative sea-level change (b, d) during January 2003–December 2013. The difference in the spectrum of energy distribution is also shown (e, f). Results are computed in the CM reference frame with the rotational feedback accounted for.
Based on CSR, GFZ, and JPL Stokes coefficients, we provide with this article monthly SH coefficients of
-
model forcing function, Flm(t);
-
geoid height change, [Xlm(t)+Ylm(t)];
-
vertical bedrock motion, ; and
-
relative sea-level change, Slm(t),
computed in both CM and CF reference frames with and without the rotational feedback included. Effects of Earth's rotation and the reference frame origin on select fields are shown in Fig. 5. The SH coefficients for sea-surface height may be obtained by summing coefficients for bedrock motion and those for relative sea-level change (see Eq. 1). While one may readily assemble these coefficients in an SH domain to retrieve the corresponding monthly fields, we also supply gridded solutions for user convenience.
We provide uncertainty associated with monthly fields as well, both in terms of spatial maps and SH coefficients. Quantification of the uncertainty is determined by the following recipe. Based on the JPL Release-06 (GIA uncorrected) mascon solutions and associated standard errors (Watkins et al., 2015; Wiese et al., 2016), we use a Monte Carlo approach to generate 5000 ensemble members of monthly land water storage solutions. We apply a unique GIA correction, computed by Caron et al. (2018), to each of these ensemble members. Next we solve the sea-level equation to derive an equivalent number of solutions for , , and other fields. Finally, we quantify the standard errors associated with each field, weighted by the likelihood of each GIA model (Caron et al., 2018). Figure 3 shows our estimates of standard errors associated with the trends in land water storage and relative sea level.
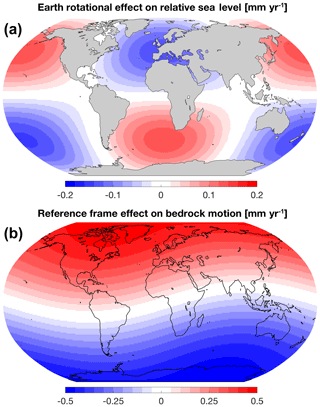
Figure 5Effects of (a) Earth's rotation and (b) reference frame on model solutions. Rotational feedback on the relative sea-level change exhibits a degree 2 spherical harmonic pattern and generally accounts for ≈10 % of the total signal (compare with Fig. 3c). Degree 1 load Love numbers depend on the choice of reference frame origin. The effect of reference frame – quantified here as the model solution computed in the CM frame minus the solution computed in the CF frame – is more pronounced in the vertical bedrock motion and the geoid height change (not shown). These results are based on JPL Stokes coefficients for the period April 2002 to March 2016.
The utility of the data we provide is that they may be used to rigorously remove those patterns that are attributable to geoid height change and bedrock motions caused by on-land mass changes from ocean altimetry, bottom-pressure, and tide gauge studies. Such removal is essential for future studies of the patterns of sea-level change owing to internal variability of the climate system which drives changes in ocean density, fresh water fluxes, and circulation (e.g., Bilbao et al., 2015; Fasullo and Nerem, 2018).
As we supply sea-level fingerprints and complementary data products with and without rotational feedback, we owe the readers some additional words of caution and recommendations. First, from the Eulerian equations of rotational motion, we solve for the feedback consistently designed for periods longer than 434 d (the period of the Chandler wobble). The rationale is that both the solid Earth and ocean pole tide (Haubrich and Munk, 1959) are removed from the satellite solutions for GRACE gravimetry and TOPEX/Poseidon and Jason altimetry on a routine basis (e.g., Wahr, 1985; Desai, 2002; Desai and Yuan, 2006). The improvements in the ocean pole tide, in fact, have been accomplished by many years of assimilation of the altimetric mission data. Hence, at periods near, or less than, 434 d, the paths to unambiguously generating solutions to the sea-level equation with centrifugal potential and loading changes from the pole tide are unclear. We might assume that the relevant feedbacks are largely removed as a processing step in rendering Level 1-b and Level 2 GRACE data products. We keep, however, rotational feedback effects of an interannual nature in one set of monthly solutions, and another set of solutions lack these effects. The users of these data should understand the differences, as those employing approaches to using the data to evaluate altimetric time series of order 10 years in length will certainly be interested in using the rotational feedback version for the analysis of interannual trends and variability adjacent to Greenland, for example Müller et al. (2019), whereas users focusing on seasonal timescale fingerprints are recommended to employ those coefficients that lack the rotational feedback, as the altimetry and space gravimetry products employed likely have the sea-surface height and gravity effects of the annual polar motion, Chandler wobble, and associated pole tides removed.
It is also worthwhile to note that on timescales of decades the mantle primarily behaves elastically, perhaps with the exception at places where the tectonic history has brought heat, volatiles, and changes in mineral structure, such as water or reduced grain size, into the region, thus reducing the effective viscosity to values below about 5×1018 Pa s (e.g., Lange et al., 2014; Mitrovica et al., 2018; Nield et al., 2018). At such low values of viscosity in the upper mantle, stress relaxation can reduce both the effective influence of gravitational loading and the amplitude of fingerprints. While we acknowledge that this effect is quite difficult to quantify, it should be a second-order effect.
We presently store data in a public repository hosted by Harvard Dataverse (https://doi.org/10.7910/DVN/8UC8IR; Adhikari et al., 2019).
The first set of data we supply are SH coefficients of global field variables. The zip file “SLFsh_coefficients.zip” contains a total of 1780 data files: 133×4 for GFZ and 156×4 each for CSR and JPL. For the given data center, four files are provided for a particular GRACE month: with and without Earth's rotational feedback included while solving for sea-level fingerprints in both CM and CF reference frames. File names follow the GRACE naming convention. Solutions that correspond to the GSM file “GSM-2_2002095-2002120_GRAC_UTCSR_BA01_0600”, for example, are stored in four files named “SLF-2_2002095-2002120_GRAC_UTCSR_BA01_0600” under appropriate directories; we simply replace “GSM” by “SLF” to denote “sea-level fingerprints”. The time stamp (in YYYYDoY-YYYYDoY format) and the corresponding data center (five-character string containing CSR, GFZ, or JPL) also appear in the file name. The example file considered above contains sea-level fingerprint solutions for the period 95–120 d of year 2002 based on the Stokes coefficients provided by CSR. Header lines 5–7 in each file further clarify which data center the solutions correspond to, which reference frame is considered, and whether or not Earth's rotational feedback is accounted for. Each data file consists of a total of 18 columns: SH degree l, SH order m, and SH coefficients for model forcing function Flm (four columns), relative sea level Slm (four columns), geoid height change [Xlm+Ylm] (four columns), and vertical bedrock motion (four columns). For each field, the first (last) two columns store cosine (sine) coefficients for our predicted mean and 1σ uncertainty, respectively. Users should note that the finite degree 0 order 0 harmonic in the monthly SLF files represents the finite mass changes for the global oceans.
The second set of data we supply are gridded maps of global field variables. We provide a total of 12 NetCDF files: four each for CSR, GFZ, and JPL. The file “SLFgrids_GFZOP_CF_WITHrotation.nc”, for example, stores solutions based on GFZ Stokes coefficients that are computed in the CF reference frame with the rotational feedback accounted for.
In this paper we describe a data product that emerges from the Release-06 GRACE Level-2 Stokes coefficients, provided by CSR, GFZ, and JPL, which contain the basic information necessary to create monthly sea-level fingerprints, and these are general enough that they may be employed in reconstructions of vertical bedrock motion, perturbed relative sea surface, and geoid height change. We provide SH coefficients of each field and uncertainty therein, computed in both CM and CF reference frames with and without rotational feedback included. For user convenience, we also provide spatial maps at resolution.
A future space altimetry mission (Surface Water and Ocean Topography, or SWOT) is aimed at providing real-time two-dimensional imaging of the sea-surface height without the necessity of having to patch together one-dimensional profiles (e.g., Gaultier et al., 2016). In addition to providing higher resolution, this will allow improved accuracy. When coupled to GRACE-FO mapping of gravity changes, we should begin to see the emergence of sea-level fingerprints. Perhaps more importantly, we may begin to more confidently remove a part of the ocean altimetry signal that should not be assimilated into dynamic ocean models: that which is associated with self-gravitation and loading. Here we present the effects of land-based mass transport and rotational effects, both together and separately. Recent appreciation of the effects of solid Earth elastic and viscoelastic response is now receiving increased scrutiny for the potential bias that may be introduced into the altimetry trend record when not accounting for these effects properly (e.g., Desai et al., 2015; Lickley et al., 2018). We have not treated the influences of GIA on rotational deformation and/or the associated axial displacement of the centrifugal potential, although we have employed the GIA model of Caron et al. (2018) to analyze GRACE Level-2 for proper representation of the monthly water height equivalent masses. As a consequence, users of the data that we supply here should understand that folding the fingerprints into analyses of any geodetic data, including tide gauges and ocean altimetry, might want to carefully consider that the secular polar motion effects in the Release-06 GRACE Level-2 products (Wahr et al., 2015; Bettadpur, 2018) have been removed and that the sea-surface height variability associated with polar drift, annual, and Chandler wobble effect is currently removed from ocean altimetry data in the manner described by Desai et al. (2015). This fact allows users to rather straightforwardly remove land-mass-change-related fingerprints from either GRACE, ocean altimetry, tide gauge, or GPS-determined vertical land motion data from April 2002 to August 2016 using the monthly solutions we supply here as a data product.
The fundamental theoretical concept of the so-called sea-level fingerprint is summarized in Sect. 2. Here we provide explicit mathematical expressions for all of the terms appearing in Eq. (4).
-
The barystatic term is given by
where
is the ocean surface area, a is already defined in Eq. (10), and 𝕊 is the surface domain of a unit sphere. The term enclosed by brackets in Eq. (A1) yields the net change in continental water volume.
-
Changes in gravitational potential, Φg, and associated changes in Earth's surface displacement, Ug, are obtained by convolving the surface loading function (Eq. 3) with respective Green's functions, 𝒢Φ and 𝒢U, as follows:
where are the variable coordinates. These variable coordinates at which the loading function is defined are related to (θ,ϕ) at which Φg and Ug are evaluated via the great-circle distance, α, as follows: . Green's functions are represented in the Legendre transform domain as follows:
where 𝒫l are Legendre polynomials (Eq. B3), and and are the load Love numbers.
-
Changes in rotational potential, Φr, and associated changes in Earth's surface displacement, Ur, follow from the Eulerian theory of rotation (Lambeck, 1980):
where 𝒴lm are degree l order m spherical harmonics (Eq. B2), Λlm are SH coefficients of perturbation in rotational potential, and k2 and h2 are degree 2 tidal Love numbers. We may express changes in rotational potential in terms of changes in Earth's rotation parameters, moment of inertia, and hence surface loading function. Considering leading-order terms only, we get the following nonzero coefficients (Milne and Mitrovica, 1998):
and
where Ω is the Earth's mean rotational velocity, 𝔸 and ℂ are the mean equatorial and polar moment of inertia, respectively, σ0 is the so-called Chandler wobble frequency, and Llm are SH coefficients of the surface loading function (Eq. B11). Note that the terms inside brackets represent changes in Earth's moment of inertia: ΔI11 and ΔI22 (Eq. A6) and ΔI33 (Eq. A7). Similarly, the terms enclosed by outer parentheses represent Earth's rotation parameters: polar motion (m1,m2) (Eq. A6) and change in length of day m3 (Eq. A7).
-
The ocean-averaged term in Eq. (4), denoted by 〈*〉, may be written as follows:
When rotational feedback is excluded, Φ and U should be replaced by Φg and Ug, respectively.
B1 Primer
-
Spherical harmonics. For brevity, we define and drop explicit dependence of a function on time so that . Any square-integrable function f(ω) can be expanded as the infinite sum of SHs as follows:
where flm are SH coefficients, and 𝒴lm(ω) are (real) normalized SHs of degree l and order m. These SHs may be expressed in terms of associated Legendre polynomials, , as follows:
where δ0m is the Kronecker delta. For and m≥0, polynomials 𝒫lm(x) are given by
where
are the Legendre polynomials. This definition of SHs and their normalization are consistent with those employed for GRACE data generation and processing (Bettadpur, 2018) and can be evaluated straightforwardly, for example, using MATLAB's associated Legendre functions (https://www.mathworks.com/help/matlab/ref/legendre.html, last access: 7 May 2019).
-
SH addition theorem. It is useful to note here that the following relationship holds:
where α once again is the great-circle distance between coordinates ω and ω′.
-
Evaluation of SH coefficients. For the chosen normalization, SHs obey the following orthogonality relationship
where and are Kronecker deltas. Using this property, SH coefficients of f(ω) are obtained as follows:
-
Evaluation of surface integrals on a unit sphere. We discretize the surface of a unit sphere using the so-called icosahedral pixelization method (Tegmark, 1996). It yields uniformly distributed quadrature points with equal pixel area. This makes numerical integration fairly straightforward as follows:
where ωj is the centroid of the jth pixel, and NT is the total number of pixels. Note that the factor 4π∕NT represents the area of each pixel on the surface of a unit sphere.
B2 SH coefficients of some basic functions
-
Ocean function. By definition, the ocean function is given by
where 𝕊O is the ocean surface domain on a unit sphere. As in Eq. (B1), we may write
Following Eq. (B6) and using the definition of ocean function, we get
where integration is performed only within the ocean surface domain. Following Eq. (B7), we obtain
-
Model forcing function. By definition, . We may write
where 𝕊C is the continental domain on a unit sphere. We derive H(ω) from the GRACE Stokes coefficients as detailed in Sect. 3. Following Eq. (B7), we get
-
Global surface loading function. Since , we may write SH coefficients of L (Eq. 3) as follows:
B3 Some useful integrals and barystatic sea level
-
Ocean surface area on a unit sphere. Since 𝒴00(w)=1 (see Appendix B1), the SH coefficient of the ocean function (Eq. B9) for l=0 and m=0 is given by
where NO is the number of pixels in the ocean surface domain 𝕊O. Since the term enclosed by parentheses represents the area of each pixel, the total area of ocean surface (i.e., NO times the pixel area) on a unit sphere is given by
-
Continental water volume on a unit sphere. The SH coefficient of the forcing function (B10) for is given by
Since the term enclosed by parentheses represents the area of each pixel, the sum of the bracketed term over 𝕊C essentially yields the total continental water volume. Consequently, we may write
-
Barystatic sea level. Using Eqs. (A1), (A2), (B13), and (B15), we get
B4 SH coefficients appearing in the sea-level equation
-
The coefficient . This coefficient is used as the first guess solution of (Eq. 8) and remains unchanged during the recursive process. Recalling that and that E is a spatial invariant, we may write
Noting that the integral is equivalent to 4π𝒪lm (see Eq. B6), and using Eq. (B16), we get
-
Other hatted coefficients. All of the coefficients appearing in Eq. (8) may be evaluated in a similar manner. Consider , for example. Recalling the definition that , and following Eq. (B6), we may write
Using the definition of ocean function, and expanding X(ω) as in Eq. (B1), we get
Following Eq. (B7), we evaluate the integral as follows:
-
The coefficient Xpq. By definition, . Using Eqs. (A3) and (A4), we may write
Using the SH addition theorem (Eq. B4), and expanding L(ω′) as in Eq. (B1), we get
or
Using the SH orthogonality relationship (Eq. B5), we get
Using Eqs. (B6) and (B19), SH coefficients Xpq are given by
Rearranging terms and applying the orthogonality relationship (Eq. B5), we obtain
-
The coefficient Ypq. By definition, . Using Eqs. (A5) and (B6), SH coefficients Ypq are given by
Rearranging terms and applying the orthogonality relationship (Eq. B5), we get
-
The coefficient Ppq. By definition, . Using Eqs. (A3) and (A4), and following the procedure to derive Xpq (Eq. B20), we obtain
-
The coefficient Qpq. By definition, . Using Eq. (A5), and following the procedure to derive Ypq (Eq. B21), we get
-
The coefficient Cpq. By definition, . Using Eqs. (A5) and (B19) and similar equations for P, we may write
Using Eqs. (B8) and (B16), we get
Note that C and all of the right-hand side terms are spatially invariant. Using Eqs. (B6) and (B24), we get
Since 𝒴00(ω)=1, we introduce a virtual expression 𝒴00(ω) inside the integral and use Eq. (B5) to find
The terms inside the braces vanish when rotational feedback is not included. Note that the first term on the right-hand side of Eq. (B21) and the first term inside the braces above cancel out while solving Eq. (9). It is, however, important to consider these terms explicitly for a clean isolation of SH coefficients of the desired fields.
B5 Summary
Here we briefly outline the workflow of our computation.
-
Given the on-land change in water equivalent height over the time period t, we compute SH coefficients of the model forcing function Flm using Eq. (B10).
-
We compute SH coefficients of the “global loading function” Llm (Eq. B11) by initializing , such that , where is given by Eq. (B17).
-
Once , and hence Llm, are initialized, we solve the recursion equation for (Eq. 8) until the solution is converged. The hatted SH coefficients appearing in Eq. (8) are expressed in terms of their non-hatted counterparts as in, for example, Eq. (B18). For the chosen solid Earth model and the reference frame origin, we compute these non-hatted coefficients using Eqs. (B20)–(B23) and (B25).
-
The choice of the solid Earth model determines the load Love numbers and and the tidal Love numbers k2 and h2. In this study, we consider the Preliminary Reference Earth Model (Dziewonski and Anderson, 1981).
-
The choice of the reference frame origin determines the degree 1 load Love numbers. In this study, we take the values from Blewitt (2003) for the CM and CF reference frames.
-
Rotational feedback is accounted for via Eqs. (B21), (B23), and (B25); SH coefficients of perturbation in rotational potential Λpq appearing in these equations are given by Eqs. (A6) and (A7). To deactivate this feedback, we set Ypq=0 (Eq. B21) and Qpq=0 (Eq. B23) and remove the terms enclosed by braces in Eq. (B25).
-
As for the convergence criterion, we track the relative change in L-2 norm after each recursion and call the solution converged when it is less than 0.001 % of the L-2 norm of the solution itself. This level of solution convergence is typically achieved after four to six iterations.
-
Unless stated otherwise, constants and parameters used in this study are taken directly from Table 1 of Adhikari et al. (2016).
-
-
Once the solution is converged for , we appropriately combine corresponding non-hatted coefficients (i.e., Eqs. B20–B23 and B25) in order to retrieve SH coefficients of relative sea level Spq (Eq. 8), geoid height change [Xpq+Ypq], and vertical bedrock motion . We supply these coefficients along with corresponding spatial maps.
SA and ERI conceived the research and wrote the first draft of the paper. SA formulated the sea-level solver, with the help of ERI, and led the calculations, with the help of FWL (in estimating degree 1 Stokes coefficients) and TF and LC (in uncertainty quantification). All authors contributed to the analysis of the results and to the writing and editing of the paper.
The authors declare that they have no conflict of interest.
This research was carried out at the Jet Propulsion Laboratory (JPL), California Institute of Technology, under a contract with National Aeronautics and Space Administration (NASA). Constructive comments from the reviewers greatly improved the quality of the paper.
This research was supported by the JPL Research, Technology & Development Program (grant no. 01-STCR-R.17.235.118; 2017–2019) and the NASA Sea-Level Change Science Team (grant no. 16-SLCT16-0015; 2018–2020), as well as the NASA MEaSUREs program (grant no. 17-MEASURES-0031; 2019–2023).
This paper was edited by Giuseppe M. R. Manzella and reviewed by Don Chambers, Xuebin Zhang, and Makan A. Karegar.
Adhikari, S. and Ivins, E. R.: Climate-driven polar motion: 2003–2015, Sci. Adv., 2, e1501693, https://doi.org/10.1126/sciadv.1501693, 2016. a, b, c
Adhikari, S., Ivins, E. R., and Larour, E.: ISSM-SESAW v1.0: mesh-based computation of gravitationally consistent sea-level and geodetic signatures caused by cryosphere and climate driven mass change, Geosci. Model Dev., 9, 1087–1109, https://doi.org/10.5194/gmd-9-1087-2016, 2016. a, b, c, d
Adhikari, S., Ivins, E. R., Frederikse, T., Landerer, F. W., and Caron, L.: Changes in relative sea-level, geoid height, and bedrock displacement derived from the Release-06 GRACE Level-2 monthly Stokes coefficients, Harvard Dataverse, V2, https://doi.org/10.7910/DVN/8UC8IR, 2019. a, b
Bettadpur, S.: Gravity Recovery and Climate Experiment Level – 2 Gravity Field Product User Handbook, GRACE 327-734 (CSR-G-03-01) (Rev 4.0, 25 April 2018), available at: ftp://podaac.jpl.nasa.gov/allData/grace/docs/L2-UserHandbook_v4.0.pdf (last access: 7 May 2019), 2018. a, b, c
Bilbao, R. A., Gregory, J. M., and Bouttes, N.: Analysis of the regional pattern of sea level change due to ocean dynamics and density change for 1993–2099 in observations and CMIP5 AOGCMs, Clim. Dynam., 45, 2647–2666, https://doi.org/10.1007/s00382-015-2499-z, 2015. a
Blewitt, G.: Self-consistency in reference frames, geocenter definition, and surface loading of the solid Earth, J. Geophys. Res., 108, B2-2103, https://doi.org/10.1029/2002JB002082, 2003. a
Caron, L., Ivins, E. R., Larour, E., Adhikari, S., Nilsson, J., and Blewitt, G.: GIA model statistics for GRACE hydrology, cryosphere and ocean science, Geophys. Res. Lett., 45, 2203–2212, https://doi.org/10.1002/2017GL076644, 2018. a, b, c, d
Chambers, D. P.: Evaluation of new GRACE time-variable gravity data over the ocean, Geophys. Res. Lett., 33, L17603, https://doi.org/10.1029/2006GL027296, 2006. a
Chambers, D. P. and Willis, J. K.: Analysis of large-scale ocean bottom pressure variability in the North Pacific, J. Geophys. Res., 113, C11003, https://doi.org/10.1029/2008JC004930, 2008. a
Cheng, M. K. and Ries, J. C.: The unexpected signal in GRACE estimates of C20, J. Geod., 91, 897–914, https://doi.org/10.1007/s00190-016-0995-5, 2017. a
Cheng, M. K., Ries, J. C., and Tapley, B. D.: Variations of the Earth's figure axis from satellite laser ranging and GRACE, J. Geophys. Res., 116, B01409, https://doi.org/10.1029/2010JB000850, 2011. a
Clark, J. A., Haidle, P. E., and Cunningham, N. L.: Comparison of satellite altimetry to tide gauge measurement of sea level: Predictions of glacio-isostatic adjustment, J. Climate, 15, 22, 3291–3300, https://doi.org/10.1175/1520-0442(2002)015<3291:COSATT>2.0.CO;2, 2002. a
Davis, J. L. and Vinogradova, N. T.: Causes of accelerating sea-level on the East Coast of North America, Geophys. Res. Lett., 44, 5133–5141, https://doi.org/10.1002/2017GL072845, 2017. a
Desai, S. D.: Observing the pole tide with satellite altimetry, J. Geophys. Res., 107, 3186, https://doi.org/10.1029/2001JC001224, 2002. a
Desai, S. D. and Yuan, D.-N.: Application of the convolution formalism to the ocean tide potential: Results from the Gravity Recovery and Climate Experiment (GRACE), J. Geophys. Res., 111, C06023, https://doi.org/10.1029/2005JC003361, 2006. a
Desai, S. D., Wahr, J., and Beckley, B.: Revisiting the pole tide for and from satellite altimetry, J. Geod., 89, 1233–1243, https://doi.org/10.1007/s00190-015-0848-7, 2015. a, b
Dieng, H. B., Cazenave, A., von Schuckmann, K., Ablain, M., and Meyssignac, B.: Sea level budget over 2005–2013: missing contributions and data errors, Ocean Sci., 11, 789–802, https://doi.org/10.5194/os-11-789-2015, 2015. a
Dobslaw, H., Bergmann-Wolf, I., Dill, R., Poropat, L., Thomas, M., Dahle, C., Esselborn, S., Konig, R., and Flechtner, F.: A new high-resolution model of non-tidal atmosphere and ocean mass variability for de-aliasing of satellite gravity observations: AOD1B RL06, Geophys. J. Int., 211, 263–269, https://doi.org/10.1093/gji/ggx302, 2017. a
Dziewonski, A. M. and Anderson, D. L.: Preliminary reference Earth model, Earth Planet. Inter., 25, 297–356, https://doi.org/10.1016/0031-9201(81)90046-7, 1981. a
Farrell, W. E. and Clark, J. A.: On postglacial sea level, Geophys. J. Roy. Astr. S., 46, 647–667, https://doi.org/10.1111/j.1365-246X.1976.tb01252.x, 1976. a
Fasullo, J. T. and Nerem, R. S.: Altimeter-era emergence of the patterns of forced sea-level rise in climate models and implications for the future, P. Natl. Acad. Sci. USA, 115, 12944–12949, https://doi.org/10.1073/pnas.1813233115, 2018. a
Frederikse, T., Jevrejeva, S., Riva, R. E. M., and Dangendorf, S.: A consistent sea-level reconstruction and its budget on basin and global scales over 1958–2014, J. Climate, 31, 1267–1280, https://doi.org/10.1175/JCLI-D-17-0502.1, 2018. a
Galassi, G. and Spada, G.: Tide gauge observations in Antarctica (1958–2014) and recent ice loss, Antarct. Sci., 29, 369–381, https://doi.org/10.1017/S0954102016000729, 2017. a
Gaultier, L., Ubelmann, C. and Fu, L.-L.: The challenge of using future SWOT data for oceanic field reconstruction, J. Atmos. Ocean. Tech., 33, 119–126, https://doi.org/10.1175/JTECH-D-15-0160.1, 2016. a
Han, S.-C., Sauber, J., and Pollitz, F.: Coseismic compression/dilatation and viscoelastic uplift/subsidence following the 2012 Indian Ocean earthquakes quantified from satellite gravity observations, Geophys. Res. Lett., 42, 3764–3722, https://doi.org/10.1002/2015GL063819, 2015. a
Han, S.-C., Sauber, J., and Pollitz, F.: Postseismic gravity change after the 2006–2007 great earthquake doublet and constraints on the asthenosphere structure in the central Kuril Islands, Geophys. Res. Lett., 43, 3169–3177, https://doi.org/10.1002/2016GL068167, 2016. a
Haubrich, R. and Munk, W.: The pole tide, J. Geophys. Res., 64, 2373–2388, https://doi.org/10.1029/JZ064i012p02373, 1959. a
Hirschi, M. and Seneviratne, S. I.: Basin-scale water-balance dataset (BSWB): an update, Earth Syst. Sci. Data, 9, 251–258, https://doi.org/10.5194/essd-9-251-2017, 2017. a
Hsu, C.-W. and Velicogna, I.: Detection of sea level fingerprints derived from GRACE gravity data, Geophys. Res. Lett., 44, 8953–8961, https://doi.org/10.1002/2017GL074070, 2017. a
Ivins, E. R., Watkins, M. M., Yuan, D.-N., Dietrich, R., Casassa, G., and Rülke, A.: On-land ice loss and glacial isostatic adjustment at the Drake Passage: 2003–2009, J. Geophys. Res., 116, B02403, https://doi.org/10.1029/2010JB007607, 2011. a
Ivins, E. R., James, T. S., Wahr, J., Schrama, E. J. O., Landerer, F. W., and Simon, K. M.: Antarctic contribution to sea-level rise observed by GRACE with improved GIA correction, J. Geophys. Res., 118, 3126–3141, https://doi.org/10.1002/jgrb.50208, 2013. a
Jacob, T., Wahr, J., Pfeffer, W. T., and Swenson, S.: Recent contributions of glaciers and ice caps to sea level rise, Nature, 482, 514–518, https://doi.org/10.1038/nature10847, 2012. a
Johnson, G. F. and Chambers, D. P.: Ocean bottom pressure seasonal cycles and decadal trends from GRACE release-05: Ocean circulation implications, J. Geophys. Res., 118, 4228–4240, https://doi.org/10.1002/jgrc.20307, 2013. a
King, M. A. and Santamaría-Gómez, A.: Ongoing deformation of Antarctica following recent Great Earthquakes, Geophys. Res. Lett., 43, 1918–1927, https://doi.org/10.1002/2016GL067773, 2016. a
Lambeck, K.: The Earth's Variable Rotation: Geophysical Causes and Consequnces, Cambridge Univ. Press, Cambridge, UK, 449 pp., 1981. a, b
Lambert, A. and Beaumont, C.: Nano-variations in gravity due to seasonal groundwater movements: implications for gravitational detection of tectonic movements, J. Geophys. Res., 82, 297–306, https://doi.org/10.1029/JB082i002p00297, 1977. a
Landerer, F. W. and Swenson, S. C.: Accuracy of scaled GRACE terrestrial water storage estimates, Water Resour. Res., 48, W04531, https://doi.org/10.1029/2011WR011453, 2012. a
Landerer, F. W., Wiese, D. N., Bentel, K., Böning, C., and Watkins, M. M.: North Atlantic meridional overturning circulation variations from GRACE ocean bottom pressure anomalies, Geophys. Res. Lett., 42, 8114–8121, https://doi.org/10.1002/2015GL065730, 2015. a
Lange, H., Casassa, G., Ivins, E. R., Schröder, L., Fritsche, M., Richter, A., Groh, A., and Dietrich, R.: Observed crustal uplift near the Southern Patagonian Icefield constrains improved viscoelastic Earth models, Geophys. Res. Lett., 41, 805–812, https://doi.org/10.1002/2013GL058419, 2014. a
Larour, E., Ivins, E. R., and Adhikari, S.: Should coastal planners have concern over where land ice is melting?, Sci. Adv., 3, e1700537, https://doi.org/10.1126/sciadv.1700537, 2017. a
Lickley, M. J., Hay, C. C., Tamisiea, M. E., and Mitrovica, J. X.: Bias in estimates of global mean sea level change inferred from satellite altimetry, J. Climate, 31, 5263–5271, https://doi.org/10.1175/JCLI-D-18-0024.1, 2018. a
Luthcke, S. B., Sabaka, T. J., Loomis, B. D., Arendt, A. A., McCarthy, J. J., and Camp, J.: Antarctica, Greenland and Gulf of Alaska land-ice evolution from an iterated GRACE global mascon solution, J. Glaciol., 59, 613–631, https://doi.org/10.3189/2013JoG12J147, 2013. a
Mazloff, M. R. and Böning, C.: Rapid variability of Antarctic Bottom Water transport into the Pacific Ocean inferred from GRACE, Geophys. Res. Lett., 43, 3822–3829, https://doi.org/10.1002/2016gl068474, 2016. a
Milne, G. A. and Mitrovica, J.: Postglacial sea-level change on a rotating Earth, Geophys. J. Int., 133, 1–19, https://doi.org/10.1046/j.1365-246X.1998.1331455.x, 1998. a, b
Mitrovica, J. X. and Peltier, W. R.: On post-glacial geoid subsidence over the equatorial ocean, J. Geophys. Res., 96, 20053–20071, https://doi.org/10.1029/91JB01284, 1991. a, b
Mitrovica, J. X., Tamisiea, M. E., Davis, J. L., and Milne, G. A.: Recent mass balance of polar ice sheets inferred from patterns of global sea-level change, Nature, 409, 1026–1029, https://doi.org/10.1038/35059054, 2001. a
Mitrovica, J. X., Hay, C. C., Kopp, R. E., Harig, C., and Latychev, K.: Quantifying the sensitivity of sea level change in coastal localities to the geometry of polar ice mass flux, J. Climate, 31, 3701–3709, https://doi.org/10.1175/JCLI-D-17-0465.1, 2018. a, b
Müller, F. L., Wekerle, C., Dettmering, D., Passaro, M., Bosch, W., and Seitz, F.: Dynamic ocean topography of the northern Nordic seas: a comparison between satellite altimetry and ocean modeling, The Cryosphere, 13, 611–626, https://doi.org/10.5194/tc-13-611-2019, 2019. a
Nield, G. A., Whitehouse, P. L., van der Wal, W., Blank, B., O'Donnell, J. P., and Stuart, G. W.: The impact of lateral variations in lithospheric thickness on glacial isostatic adjustment in West Antarctica, Geophys. J. Int., 214, 811–824, https://doi.org/10.1093/gji/ggy158, 2018. a
Peltier, W. R.: Dynamics of the Ice Age Earth, Adv. Geophys., 24, 1–146, https://doi.org/10.1016/S0065-2687(08)60519-1, 1982. a
Piecuch, C. G., Thompson, P. R., and Donohue, K. A.: Air pressure effects on sea level changes during the twentieth century, J. Geophys. Res., 121, 7917–7930, https://doi.org/10.1002/2016JC012131, 2016. a
Rapp, R. H.: The determination of geoid undulations and gravity anomalies from SEASAT altimeter data, J. Geophys. Res., 88, 1552–1562, https://doi.org/10.1029/JC088iC03p01552, 1983. a
Rietbroek, R., Brunnabend, S.-E., Kusche, J., and Schröter, J.: Resolving sea level contributions by identifying fingerprints in time-variable gravity and altimetry, J. Geodynam., 59–60, 72–81, https://doi.org/10.1016/j.jog.2011.06.007, 2012. a
Rignot, E., Velicogna, I., van den Broeke, M. R., Monaghan, A., and Lenaerts, J.: Acceleration of the contribution of the Greenland and Antarctic ice sheets to sea level rise, Geophys. Res. Lett., 38, L05503, https://doi.org/10.1029/2011GL046583, 2011. a
Riva, R. E. M., Bamber, J. L., Lavallée, D. A., and Wouters, B.: Sea-level fingerprint of continental water and ice mass change from GRACE, Geophys. Res. Lett., 37, L19605, https://doi.org/10.1029/2010GL044770, 2010. a
Rodell, M., Beaudoing, H. K., L'Ecuyer, T. S., Olson, W. S., Famiglietti, J. S., Houser, P. R., Adler, R., Bosilovich, M. G., Clayson, C. A., Chambers, D., Clark, E., Fetzer, E. J., Gao, X., Gu, G., Hilburn, K., Huffman, G. J., Lettenmaier, D. P., Liu, W. T., Robertson, F. R., Schlosser, C. A., Sheffield, J., and Wood, E. F.: The observed state of the water cycle in the early Twenty-First Century, J. Climate, 28, 8289–8317, https://doi.org/10.1175/JCLI-D-14-00555.1, 2015. a
Save, H., Bettadpur, S., and Tapley, B. D.: High-resolution CSR GRACE RL05 mascons, J. Geophys. Res., 121, 7547–7569, https://doi.org/10.1002/2016JB013007, 2016. a
Saynisch, J., Bergmann-Wolf, I., and Thomas, M.: Assimilation of GRACE-derived oceanic mass distributions with a global ocean circulation model, J. Geodesy, 89, 121–139, https://doi.org/10.1007/s00190-014-0766-0, 2015. a
Schrama, E. J. O., Wouters, B., and Rietbroek, R.: A mascon approach to assess ice sheet and glacier mass balances and their uncertainties from GRACE data, J. Geophys. Res., 119, 6048–6066, https://doi.org/10.1002/2013JB010923, 2014. a, b
Shepherd A. and the IMBIE-2 Team: Mass balance of the Antarctic Ice Sheet from 1992 to 2017, Nature, 558, 219–222, https://doi.org/10.1038/s41586-018-0179-y, 2018. a
Simon, K. M., Riva, R. E. M., Kleinherenbrink, M., and Frederikse, T.: The glacial isostatic adjustment signal at present day in northern Europe and the British Isles estimated from geodetic observations and geophysical models, Solid Earth, 9, 777–795, https://doi.org/10.5194/se-9-777-2018, 2018. a
Spada, G.: Glacial isostatic adjustment and contemporary sea level rise: An overview, Surv. Geophys., 38, 153–185, https://doi.org/10.1007/s10712-016-9379-x, 2017. a
Spada, G. and Galassi, G.: Spectral analysis of sea level during the altimetry era, and evidence for GIA and glacial melting fingerprints, Global Planet. Change, 143, 34–49, https://doi.org/10.1016/j.gloplacha.2016.05.006, 2016. a
Stammer, D., Ray, R. D., Andersen, O. B., Arbic, B. K., Bosch, W., Carrère, L., Cheng, Y., Chinn, D. S., Dushaw, B. D., Egbert, G. D., Erofeeva, S. Y., Fok, H. S., Green, J. A. M., Griffiths, S., King, M. A., Lapin, V., Lemoine, F. G., Luthcke, S. B., Lyard, F., Morison, J., Müller, M., Padman, L., Richman, J. G., Shriver, J. F., Shum, C. K., Taguchi, E., and Yi, Y.: Accuracy assessment of global barotropic ocean tide models, Rev. Geophys., 52, 243–282, https://doi.org/10.1002/2014RG000450, 2014. a
Sterenborg,, M. G., Morrow, E., and Mitrovica, J. X.: Bias in GRACE estimates of ice mass change due to accompanying sea-level change, J. Geodesy, 87, 387–392, https://doi.org/10.1007/s00190-012-0608-x, 2013. a
Stocchi, P. and Spada, G.: Influence of glacial isostatic adjustment upon current sea level variations in the Mediterranean, Tectonophysics, 474, 56–68, https://doi.org/10.1016/j.tecto.2009.01.003, 2009. a
Swenson, S., Chambers, D., and Wahr, J.: Estimating geocenter variations from a combination of GRACE and ocean model output, J. Geophys. Res., 113, B08410, https://doi.org/10.1029/2007JB005338, 2008. a
Tamisiea, M. E.: Ongoing glacial isostatic contributions to observations of sea level change, Geophys. J. Int., 186, 1036–1044, https://doi.org/10.1111/j.1365-246X.2011.05116.x, 2011. a, b
Tamisiea, M. E., Hughes, C. W., Williams, S. D. P., and Bingley, R. M.: Sea level: measuring the bounding surfaces of the ocean, Philos. T. Roy. Soc. A, 372, 20130336, https://doi.org/10.1098/rsta.2013.0336, 2014. a
Tapley, B. D., Watkins, M. M., Flechtner, F., Reigber, C., Bettadpur, S., Rodell, M., Sasgen, I., Famiglietti, J. S., Landerer, F. W., Chambers, D. P., Reager, J. T., Gardner, A. S., Save, H., Ivins, E. R., Swenson, S. C., Boening, C., Dahle, C., Wiese, D. N., Dobslaw, H., Tamisiea, M. E., and Velicogna, I.: Contributions of GRACE to understanding climate change, Nat. Clim. Change, 9, 358–369, https://doi.org/10.1038/s41558-019-0456-2, 2019. a
Tegmark, M.: An icosahedron-based method for pixelizing the celestial sphere, Astrophysical J. Lett., 470, L81–L84, https://doi.org/10.1086/310310, 1996. a
Velicogna, I.: Increasing rates of ice mass loss from the Greenland and Antarctic ice sheets revealed by GRACE, Geophys. Res. Lett., 36, L19503, https://doi.org/10.1029/2009GL040222, 2009. a
Wahr, J., Molenaar, M., and Bryan, F.: Time variability of the Earth's gravity field: Hydrological and oceanic effects and their possible detection using GRACE, J. Geophys. Res., 103, 30205–30230, https://doi.org/10.1029/98JB02844, 1998. a
Wahr, J., Nerem, R. S., and Bettadpur, S. V.: The pole tide and its effect on GRACE time-variable gravity measurements: Implications for estimates of surface mass variations, J. Geophys. Res.-Sol. Ea., 120, 4597–4615, https://doi.org/10.1002/2015JB011986, 2015. a
Wahr, J. M.: Deformation induced by polar motion, J. Geophys. Res., 90, 9363–9368, https://doi.org/10.1029/JB090iB11p09363, 1985. a
Watkins, M. M., Wiese, D. N., Yuan, D.-N., Böning, C., and Landerer, F. W.: Improved methods for observing Earth's time variable mass distribution with GRACE, J. Geophys. Res.-Sol. Ea., 120, 2648–2671, https://doi.org/10.1002/2014JB011547, 2015. a, b, c
WCRP Global Sea Level Budget Group: Global sea-level budget 1993–present, Earth Syst. Sci. Data, 10, 1551–1590, https://doi.org/10.5194/essd-10-1551-2018, 2018. a
Wiese, D. N., Landerer, F. W., and Watkins, M. M.: Quantifying and reducing leakage errors in the JPL RL05M GRACE mascon solution, Water Resour. Res., 52, 7490–7502, https://doi.org/10.1002/2016WR019344, 2016. a, b
- Abstract
- Copyright statement
- Introduction
- Key variables and deliverables
- The sea-level equation
- GRACE and sea-level fingerprints
- Discussion
- Data availability
- Conclusions
- Appendix A: Theory of the sea-level fingerprint
- Appendix B: Spectral methods for sea-level equation
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Copyright statement
- Introduction
- Key variables and deliverables
- The sea-level equation
- GRACE and sea-level fingerprints
- Discussion
- Data availability
- Conclusions
- Appendix A: Theory of the sea-level fingerprint
- Appendix B: Spectral methods for sea-level equation
- Author contributions
- Competing interests
- Acknowledgements
- Financial support
- Review statement
- References




