AIUB-GRACE gravity field solutions for G3P: processing strategies and instrument parameterization

This paper discusses strategies to improve the Gravity Recovery And Climate Experiment (GRACE) monthly solutions computed at the Astronomical Institute of the University of Bern (AIUB) which are contributing to the Horizon 2020 project G3P – Global Gravity-based Groundwater Product. To improve the AIUB-GRACE gravity field solutions, we updated the use of the Level-1B observations, adapted the background models, and improved the processing strategies in terms of instrument screening and parameterization. We used the Release 3 K-band product (KBR) and star camera data (L1B RL03), and we adopted Release 6 of the Atmospheric and Ocean De-aliasing (AOD1B RL06) product. For the accelerometer parameterization, we used arc-wise full scale factor matrix and arc-wise third-order polynomial biases. The new accelerometer parameterization is effective in reducing noise over the oceans in gravity field solutions, especially for the late years of the GRACE mission when the thermal control was switched off. In this paper, we show that the outliers in the KBR antenna offset correction (AOC) are projected into the range rate residuals; therefore, we used the KBR AOC as the main source for outlier detection and eliminated the AOC above a threshold for all data before the gravity field processing. The full time series of GRACE AIUB-G3P gravity field solutions (Darbeheshti et al., 2023b) is available at https://doi.org/10.5880/ICGEM.2023.001.

1 Introduction

The Global Gravity-based Groundwater Product (G3P) is a collaborative Horizon 2020 project between 12 European institutions coordinated by the German Research Centre for Geosciences (GFZ). One of the key objectives of the G3P project is to process Gravity Recovery And Climate Experiment (GRACE, Tapley et al., 2004) and GRACE Follow-On (GRACE-FO, Tapley et al., 2019) Level-1B instrument data. GRACE and GRACE-FO provide a unique type of Earth observation from space (Wahr et al., 1998), total water storage variations on the continents, which is essential to calculate the variations in groundwater storage by subtracting other compartments of water storage variations such as glaciers, snow, soil moisture, and surface water bodies derived from other Earth observation data or models.

Petit and Luzum (2010)Lyard et al. (2021)Dobslaw et al. (2017)Petit and Luzum (2010)Desai (2002)Folkner et al. (2009)

Table 1 Background models for AIUB-G3P with maximum spherical harmonic degree (d/o) (if applicable).

Table 2 Data products for AIUB-G3P.

The Astronomical Institute of the University of Bern (AIUB) is one of the GRACE/GRACE-FO analysis centers contributing to the G3P project. AIUB has produced monthly GRACE gravity field solutions since 2011. The first monthly GRACE series was released in 2011 (Meyer et al., 2012) and the second series in 2016, AIUB-RL02 (Meyer et al., 2016). Beside the GRACE gravity field solutions, GPS-based GRACE orbits are also processed at AIUB and are made publicly available (Arnold and Jäggi, 2020). The AIUB-RL02 of monthly gravity field models contributed to the combined monthly models in the framework of the European Gravity Service for Improved Emergency Management (EGSIEM) project (Meyer et al., 2019) coordinated by AIUB (Jäggi et al., 2019). AIUB-RL02 lacks the late years of GRACE gravity field solutions in 2016 and 2017. Therefore, a new AIUB-G3P is prepared with the following objectives:

• contribute to the Global Gravity-based Groundwater Product (G3P);

• contribute to the International Association of Geodesy (IAG) service COST-G (International Combination Service for Time-variable Gravity Field Solutions) (Jäggi et al., 2020);

• update the input observations and background models for GRACE gravity field recovery to be consistent with the other contributors to the COST-G (see Sect. 2);

• improve gravity field recovery processing;

• provide the complete time series of monthly GRACE gravity field solutions from 2002 to 2017.

2 GRACE orbit dynamic model

AIUB-G3P, like its two predecessors AIUB-RL01 (Meyer et al., 2012) and AIUB-RL02 (Meyer et al., 2016), is based on the celestial mechanics approach (CMA) (Beutler et al., 2010), which treats gravity field estimation as a generalized orbit determination problem. The equations of motion for both GRACE satellites are

$$\begin{array}{}\text{(1)}& \ddot{\mathit{r}}={\mathit{a}}_{\mathrm{g}}+{\mathit{a}}_{\mathrm{ng}}+{\mathit{a}}_{\mathrm{emp}},\end{array}$$

where $\ddot{\mathit{r}}$ is the acceleration of the satellite (second time derivative of the satellite position vector), a_g denotes accelerations due to all gravitational forces, a_ng denotes accelerations due to all non-gravitational forces, and a_emp denotes empirical accelerations designed to overcome deficiencies remaining in the force models.

The CMA solves Eq. (1) as a linearized least-squares estimation where gravity field coefficients and all other orbit-related parameters are estimated together. Kinematic positions and K-band range rate data are used as observables to estimate orbit and gravity field coefficients such that the orbit trajectories are solving Eq. (1).

The gravitational models (a_g) in Eq. (1) are called the background gravity models. The details of the background gravity models for AIUB-G3P are provided in Table 1.

For a_emp, constrained piecewise constant accelerations at 15 min intervals in all three directions of the local orbital frame were estimated (Jäggi et al., 2006).

For a_ng, the GRACE accelerometer data are used. The accelerometer measurements given in the ACC1B data product are affected by unknown scale factors, biases, and random noise (Kim, 2000). Ideally, the scale factor matrix S (Eq. 2) should be an identity matrix, but it contains diagonal elements and nonzero off-diagonal elements due to small instrument imperfections causing mutual influence of the accelerometer axes among each other. In order to account for these imperfections, a fully populated scale factor matrix is used for AIUB-G3P.

$$\begin{array}{}\text{(2)}& \mathbf{S}=\left[\begin{array}{ccc}{s}_x& \mathit{\alpha }+\mathit{\zeta }& \mathit{\beta }-\mathit{ϵ}\\ \mathit{\alpha }-\mathit{\zeta }& s_y& \mathit{\gamma }+\mathit{\delta }\\ \mathit{\beta }+\mathit{ϵ}& \mathit{\gamma }-\mathit{\delta }& s_z\end{array}\right]\end{array}$$

The off-diagonal components are composed of a symmetric shear (α, β, and γ) and a skew-symmetric rotation part (ζ, ϵ, and δ). For more details on interpretation of these elements we refer to Klinger and Mayer Gürr (2016). For previous AIUB releases, the off-diagonal elements have been neglected; i.e., the scale factor matrix was assumed to have main diagonal elements only. To account for instrument imperfections and misalignment, for AIUB-G3P both main diagonal and off-diagonal elements of the scale factor matrix (see Eq. 2) were estimated on a daily basis.

To account for bias changes due to temperature variations according to Klinger and Mayer Gürr (2016), a bias vector b is estimated daily using a third-order polynomial. Four coefficients were estimated in each direction; therefore, 12 accelerometer bias coefficients were estimated on a daily basis for each satellite.

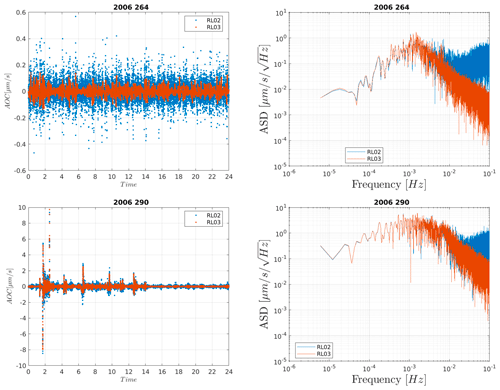
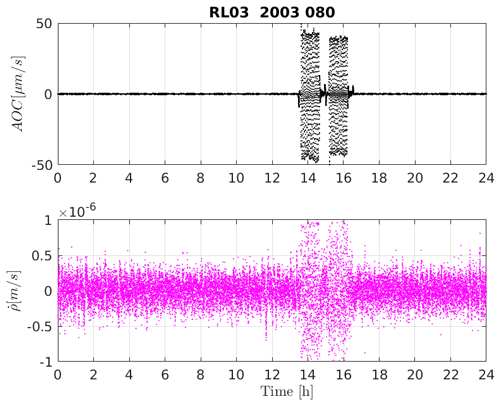
Figure 1 Range rate AOC for days 264 (no outliers) and 290 (containing outliers) with the corresponding ASD.

Table 3 Level-1B data screening: threshold-based outlier detection.

The main observations are a combination of kinematic orbit positions for each satellite and inter-satellite K-band range rate measurements. The combination is realized through daily normal equations and is accumulated for 1 month to solve for monthly spherical harmonics coefficients of the Earth's gravity field. The kinematic orbits of the GRACE satellites are determined in a precise point positioning from the undifferenced GPS phase observations (Jäggi et al., 2006). The kinematic orbits rely on reprocessed GPS orbits from the CODE analysis center (Steigenberger et al., 2011). For kinematic orbit determination, maps of the empirical phase center variation of the GRACE GPS antennas (Jäggi et al., 2009) were re-estimated. The kinematic orbits for the whole GRACE lifetime can be downloaded from http://ftp.aiub.unibe.ch/LEO_ORBITS/GRACE/RL01/ (last access: 19 March 2024). The specifics of the GRACE data products are given in the Table 2.

Although we cannot see the star camera data in Eq. (1) explicitly, they appear implicitly in two ways in GRACE gravity field recovery:

• transforming the linear ACC1B product to inertial frame (Darbeheshti et al., 2017) and

• calculating the KBR antenna offset correction in the KBR1B product.

The SCA1B product is used to define the KBR antenna offset correction (AOC) in the KBR1B product. The KBR instrument measures the distance between the antenna phase centers, which are placed nominally on the satellite frame x axis, almost 1.5 m away from the satellites' center of mass. Consequently, any pointing jitter (deviations of the satellites' attitudes from their nominal attitudes) causes a geometric error in the ranging measurement. In the absence of such misplacements and in the absence of pointing jitter, this effect would be constant and hence not effect the measured (biased) KBR range. The GRACE KBR1B data product files contain a column, which is called antenna offset correction (AOC) term (Case et al., 2010). It has to be added to the KBR ranging measurement. A second column and third column are also provided, computed by numerical differentiation, describing the correction for range rate and range acceleration.

Although the AOC is improved in GRACE KBR1B RL03, AOC outliers exist and need to be removed. AOC rate is in the range of ±0.5 µm s⁻¹ (Klinger, 2018); therefore, values beyond ±1 µm s⁻¹ are considered outliers. Figure 1 shows range rate AOC columns from GRACE KBR1B RL02 and GRACE KBR1B RL03 for 2 d in 2006. There are no outliers on day 264, but for both RL02 and RL03, day 290 contains outliers. The corresponding amplitude spectral density (ASD) plot of these 2 d shows that although the high-frequency noise (greater than 10⁻² µm s⁻¹ Hz^−0.5) has been filtered out from the AOC, AOC RL03 still contains outliers that correspond to the satellite events like calibration maneuvers for different instruments.

3 Pre-processing: Level-1B data screening

In theory, the GRACE L1B data products can be used directly for gravity field recovery, but there are outliers in the data that need to be removed before the gravity field recovery processing. Data screening for 15 years of GRACE data and for every instrument is a challenging task. The cause of systematic errors and outliers has been studied by Goswami (2018) and Klinger (2018). In this work we have only focused on finding an effective way to find outliers in GRACE data.

The overall error (including outliers) in the instrument data and background models is projected in range rate residuals in the case of GRACE gravity field recovery. Figure 2 shows how outliers in range rate AOC are mapped into range rate pre-fit residuals.

Figure 2 Outliers in AOC (day 80, 2003) are mapped into the KBR range rate pre-fit residuals.

3.1 AOC and ACC screening

AIUB-RL02 screening was based on inspection of the range rate residuals and removing outliers by gap tables (Meyer et al., 2016). For AIUB-G3P, a novel screening strategy has been developed. This approach involves scrutinizing the GRACE L1B data product, specifically KBR1B and ACC1B. When an outlier is identified in the daily KBR1B and ACC1B, the corresponding day is flagged. Subsequently, the epoch of the outlier is excluded using monthly session tables in the Bernese software.

The AIUB GRACE gravity field solutions are constructed by estimating orbital parameters for each 24 arc hour period. The epochs of these daily arcs are recorded in the session tables. In the presence of an outlier, the affected epoch is removed, leading to the segmentation of the daily arc. New orbital parameters are then estimated for the revised arcs. As a result, while the general AIUB monthly gravity solution is typically based on daily arcs, months with outliers in the instrument exhibit shorter arcs in the monthly gravity solution.

We performed the data screening in three major steps: (1) threshold-based outlier detection of KBR1B AOC rate data product, (2) threshold-based outlier detection of ACC1B data product, and (3) empirical elimination of days that degraded final monthly gravity field solution. Table 3 summarizes the threshold values and margins used for threshold-based outlier detection for first and second steps. Margin means the time span before and after an outlier detected in the data. We used absolute value thresholds for the AOC rate data product because the AOC rate is in the range of ±0.5 µm s⁻¹. For the ACC1B data product, we used the daily median-based threshold because we estimate ACC scale factors and biases on a daily basis.

Figure 3 shows the periods of outliers in the AOC rate and linear ACC data for GRACE A and GRACE B in all three axes. The years 2006 and 2007 are representative of the high quality of GRACE data. There are 12 complete months of instrument data products from 2003 to 2010; therefore, there is no data gap in the AOC rate and linear ACC data for the years 2006 and 2007. GRACE data products are only available until the end of June 2017. Since April 2011, the onboard instruments have been shut down for approximately 40–50 d during each 161 d to extend the GRACE battery lifetime; this is why there are AOC rate and linear ACC data gaps for 2016 and 2017, the last years of the GRACE lifetime, for which the quality of GRACE instrument data products is degraded.

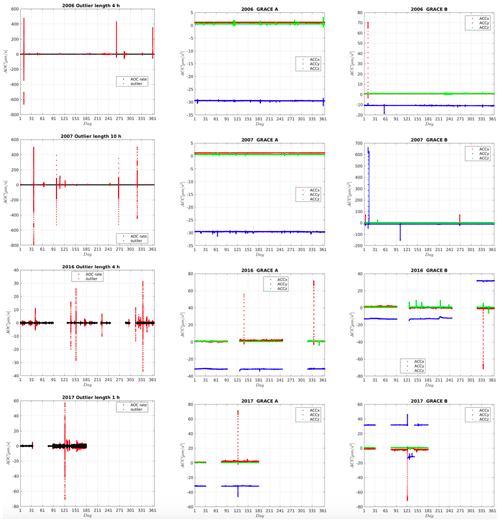
Figure 3 Annual plots of AOC rate (first column) and ACC1B accelerometer linear accelerations along three axes for 2006, 2007, 2016, and 2017. Vertical red lines in the first column are outliers in AOC. For linear accelerations, vertical lines are outliers along three axes.

The first column of Fig. 3 shows that the AOC outlier time length in 2007 is more than twice that in 2006 (4 h in 2006 versus 10 h in 2007). In general, a satellite event like a calibration maneuver causes outliers in AOC. GRACE satellite events are published in the “sequence of events” file. For 2017, a much larger outlier threshold (3 µm s⁻¹) had to be used for AOC because with a 1 µm s⁻¹ AOC threshold, we would not have any data left to solve for the gravity field recovery.

Figure 4 The empirical elimination procedure for July 2011 involves iteratively removing one day at a time. In the first iteration, day 186 (denoted as 1 in the legend) is eliminated, followed by day 187 in the second iteration and day 188 in the third iteration. The consistently lower position of the red curves in these iterations suggests that days 186, 187, and 188 are corrupting the gravity solution. The legend indicates the corresponding day number eliminated in each gravity field solution.

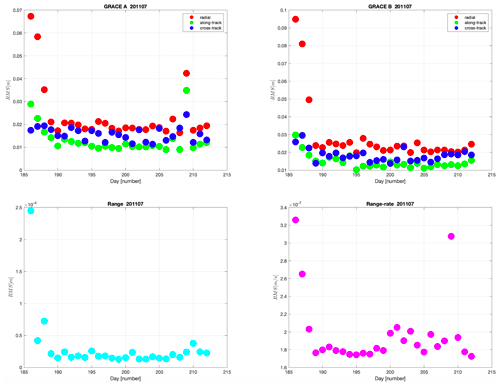
Figure 5 Daily pre-fit residual rms for GRACE A orbit – radial (red), along-track (green), and cross-track (blue) directions, as well as GRACE B orbit, range, and range rates for July 2011.

Columns 2 and 3 of Fig. 3 show that there are much fewer outliers in ACC data than AOC. GRACE A ACC data for the years 2006 and 2007 are of high quality, but there are some outliers in the GRACE B ACC data. In October 2016, the accelerometer on board GRACE B was permanently powered off to reduce the stress on the remaining battery cells. Since then, no GRACE B accelerometer data have been available (except for May 2017). To allow for gravity field recovery, the GRACE B accelerometer transplant data (Bandikova et al., 2019) have been made available. Figure 3 shows that the bias along y axis in GRACE B in November 2016 suddenly changes and follows the bias in GRACE A. This pattern continues in 2017, except in May, when real GRACE B ACC data are again available. In June 2017 the bias in GRACE B y axis is again the same as for GRACE A.

Figure 6 Difference degree amplitudes with respect to the “mean model” for GRACE (February 2011 to August 2016) for AIUB-RL02 and AIUB-G3P.

Figure 7 Weighted SD over the oceans for AIUB-RL02 and AIUB-G3P.

Figure 8 Weighted SD over the oceans for the years 2016 and 2017, where AIUB-RL02 data are available. “Diagonal” shows the AIUB-G3P setup with diagonal scale factor accelerometer parameterization and AOD-RL05 shows the AIUB-G3P setup with AOD-RL05.

3.2 Empirical elimination of whole days

The empirical elimination of entire days has been incorporated as the final stage of data screening in generating the AIUB-RL01, AIUB-RL02, and AIUB-G3P solutions. For the empirical elimination procedure, n monthly gravity field solutions are produced for each month, where n is the number of days in each month. In each gravity field solution, 1 whole day of data is eliminated. Then, by plotting and comparing the n gravity field solutions in terms of the difference degree amplitudes of geoid heights, days that corrupt the monthly gravity solution may be recognized. To compute the difference degree amplitudes, selecting a reference gravity field solution is crucial. In this context, our choice is the monthly gravity field solutions produced by the Institute of Geodesy at Graz University of Technology, ITSG-GRACE2018. This decision is motivated by the intention to benchmark our solution against a high-quality GRACE gravity solution. Furthermore, our solution closely aligns with ITSG-GRACE2018 in terms of input observations, background models, and processing strategies. The deliberate use of a monthly model takes into account the varying quality of GRACE solutions from month to month, especially towards the end of the GRACE mission. Figure 4 demonstrates this procedure for July 2011. For this month, there is a dataset spanning 27 d. In the first iteration, 27 gravity solutions were generated, each excluding 1 d (resulting in the use of 26 d per solution). The legend denotes the day number that was omitted. For example, in July 2011, in the first iteration, day 1 in the legend corresponds to day 186, day 2 to day 187, and so forth. Moving to the second iteration, day 186 is eliminated, resulting in 26 gravity solutions. In this iteration, day 1 corresponds to day 187. Subsequently, for the third iteration, day 187 is eliminated, and for the fourth iteration, day 188 is omitted. Remarkably, by the fourth iteration, after eliminating 3 entire days, all the gravity solutions converge closely. Their quality even surpasses that of the AIUB-RL02 monthly gravity field solution.

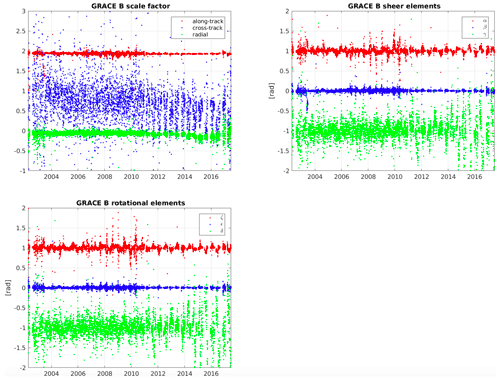
Figure 9 Elements of the scale factor matrix for GRACE B (up) main diagonal elements in the along-track, cross-track, and radial direction; for a better illustration, a constant offset of ±1 is added to the red and green graphs (middle) for shear elements and (bottom) rotational elements.

To diagnose why these 3 d corrupt the gravity field solution, it is helpful to look at pre-fit residuals (Darbeheshti et al., 2018) of observations. Pre-fit residuals in the context of gravity field recovery are observed values minus computed values, where the computed value is independent of gravity field estimation. Figure 5 shows daily root mean square (rms) of pre-fit residuals for GRACE A and GRACE B orbits, as well as ranges and range rates in July 2011. Days 186, 187, and 188 show large rms for all pre-fit residuals, which is in agreement with the empirical elimination procedure.

4 Evaluation of new AIUB-G3P GRACE

In this section, we compare new monthly GRACE solutions for the G3P project, AIUB-G3P to AIUB-RL02. To maintain consistency, all comparisons in this section are referenced to a “mean model”. The mean model was computed by averaging monthly gravity field solutions from the Center for Space Research at the University of Texas, Austin (CSR Release 06), the German Research Centre for Geosciences (GFZ Release 06), the Centre National d'Etudes Spatiales/Groupe de Recherche de Geódeśie Spatiale (CNES_GRGS_RL04), and the Institute of Geodesy at Graz University of Technology (ITSG-Grace2018) for the time period 2004–2017.

An overall comparison of the AIUB-RL02 and AIUB-G3P is shown in Fig. 6. For comparison, we only considered the months where AIUB-RL02 is available. The new AIUB-G3P shows the lower noise level, which is the result of the improvements in the processing chain.

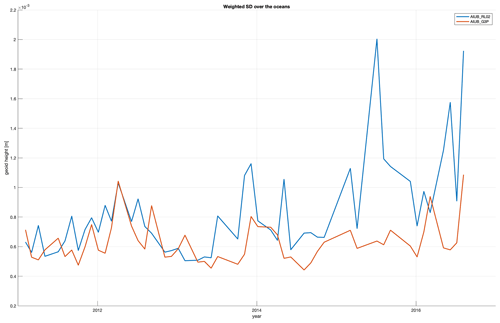
One approach for evaluating GRACE gravity monthly solutions involves calculating the standard deviation (SD) of variability over the oceans, where hydrological signals are not expected. The discrepancies between the monthly solution and the mean model are assessed on a grid with a cell size of 3°, corresponding to a spherical harmonic expansion up to degree and order 60. Secular and seasonal variations are fitted to all grid cells and subtracted to eliminate long periodic signals of oceanic origin. The grid cells are weighted by the cosine of the latitude to account for their different sizes, and the standard deviation over all ocean cells is computed. To prevent contamination from continental signals, the shoreline is shifted by three grid cells (equivalent to 9°) into the oceans (Meyer et al., 2016).

Figure 7 shows the standard deviations computed in this way for AIUB-RL02 and AIUB-G3P GRACE gravity field solutions. The AIUB-G3P solution shows a significant improvement over AIUB-RL02 in the later years of GRACE lifetime, mainly after April 2011. There are few months in 2005 and 2009 for which the gravity field solutions are slightly worse in AIUB-G3P in terms of noise over the ocean. The reason for this degradation is still unknown to us.

4.1 Major improvements in the processing chain for AIUB-G3P

As mentioned in Sect. 2, two significant changes in the processing chain have contributed to the improvement of AIUB-G3P.

• Accelerometer parameterization. In AIUB-RL02, only the diagonal elements of the scale factor matrix were calculated for each accelerometer in each arc. In AIUB-G3P, the full scale factor matrix was computed for each accelerometer in each arc, aligning with the recommendations by Klinger and Mayer Gürr (2016).

• Updating AOD release. The Atmospheric and Oceanic Dealiasing (AOD) release was updated from RL05 to RL06.

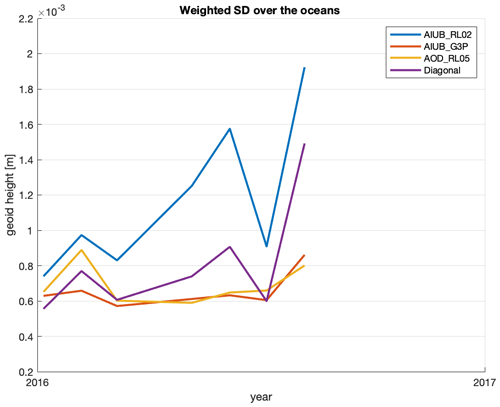
The impact of these two changes is assessed in Fig. 8 for the years 2016–2017, a period during which the quality of GRACE observations was degraded. The AIUB-RL02 solution is based on AOD-RL05 and diagonal scale factor accelerometer parameterization, while AIUB-G3P is based on AOD-RL06 and full scale factor accelerometer parameterization. In the legend AOD-RL05 indicates the same setup as AIUB-G3P, but using AOD-RL05 instead of AOD-RL06, and “diagonal” shows the same setup as AIUB-G3P, but diagonal scale factor accelerometer parameterization instead. Figure 8 shows that the full scale factor matrix for accelerometer parameterization is important for late years of GRACE data. The effect of full scale factor accelerometer parameterization is even more important than updating to AOD-RL05; as is clear from the noise over the ocean, the solution with AOD-RL05 is below the solution with diagonal scale factor accelerometer parameterization.

Figure 9 shows the elements of accelerometer full scale factor matrix for AIUB-G3P GRACE B. The main diagonal elements of the accelerometer cross-track axis are more scattered than elements of the along-track and radial axes, which is related to the smaller sensitivity of the cross-track axis compared to the other two axes. Additionally, the shear and rotational elements associated with the less sensitive cross-track axis (δ and γ) are nonzero and are increasing for the late years of GRACE. The sheer and rotational elements are absorbing accelerometer imperfections and misalignments, resulting in the better quality of AIUB-G3P than AIUB-RL02 in Fig. 7.

5 Data availability

The full time series of GRACE AIUB-G3P gravity field solutions (Darbeheshti et al., 2023b) is available at https://doi.org/10.5880/ICGEM.2023.001.

6 Conclusions

In this paper, the importance of Level-1B data pre-processing methodologies to improve GRACE gravity field solutions were demonstrated on the basis of AIUB processing chain and the transition from AIUB-RL02 (Meyer et al., 2016) to AIUB-G3P. Also the contribution of individual updates to the overall accuracy improvement of AIUB-G3P was highlighted. In particular, the effects and benefits of an automated AOC data screening, and a full scale factor accelerometer parameterization were analyzed in detail. The full time series of GRACE AIUB-G3P gravity solutions can be accessed from the website of the International Center for Global Earth Models (ICGEM, Ince et al., 2019) at http://icgem.gfz-potsdam.de/series/03_other/AIUB/AIUB-G3P.