the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Wind wave and water level dataset for Hornsund, Svalbard (2013–2021)
Mateusz Moskalik
Agnieszka Herman
Underwater pressure sensors were deployed near-continuously at various locations of the nearshore (8–23 m depth) Hornsund fjord, Svalbard, between July 2013 and February 2021. Raw pressure measurements at 1 Hz were used to derive mean water levels, wave spectra and bulk wave parameters for 1024 s bursts at hourly intervals. The procedure included subtracting atmospheric pressure, depth calculation, fast Fourier transform, correction for the decrease of the wave orbital motion with depth and adding a high-frequency tail. The dataset adds to the sparse in situ measurements of wind waves and water levels in the Arctic, and it can be used, for example, for analysing seasonal wind wave conditions and inter-annual trends and calibrating/validating wave models. The dataset is stored in the PANGAEA repository (https://doi.org/10.1594/PANGAEA.954020; Swirad et al., 2023).
- Article
(5361 KB) - Full-text XML
- BibTeX
- EndNote
In situ wave measurements are critical for understanding wave climate, analysing seasonal and inter-annual trends, and calibrating and validating wave transformation models (e.g. Reistad et al., 2011). The spatial distribution of instruments providing wind wave data is irregular and tends to concentrate in mid- and low-latitude coastal areas (e.g. https://www.ndbc.noaa.gov/, 28 November 2022; Semedo et al., 2015). In the Arctic, the network of such instruments is particularly sparse. There is a pertinent lack of continuous wave data in the Svalbard archipelago where communities, industry infrastructure, and research stations are located. Continuous wave observations in the coastal Arctic are needed to better understand how the following contribute to coastal flooding and erosion that can cause infrastructure damage (Forbes, 2011): (i) decreasing sea-ice extent – pan-Arctic annual mean extent decrease of 3.5 %–4.1 % per decade (IPCC, 2019) or 1.5- to 3-fold increase in the length of the sea-ice-free season along pan-Arctic coasts (Barnhart et al., 2014) between 1979 and 2012; (ii) increasing frequency and strength of storms (Francis et al., 2011; Wang et al., 2015; Stopa et al., 2016; Waseda et al., 2018); and, in consequence, (iii) higher waves acting on Arctic coasts for longer time periods.
Our knowledge of the western Svalbard wave climate comes primarily from global spectral models such as NOAA's WaveWatch III (WW3) hindcast (WW3DG, 2019); ECMWF reanalysis projects ERA-40 (1957–2002; Uppala et al., 2005), ERA-Interim (1979–2019; Dee et al., 2011), and ERA5 (1959–present; Hersbach et al., 2020); or NCEP's Climate Forecast System Reanalysis (CFSR; Saha et al., 2014). Arctic Ocean Wave Analysis and Forecast system (Carrasco et al., 2022) is a shorter-duration (since 2017), higher-resolution (3 km) model that provides hourly significant wave height (Hs), peak period (Tp) and peak wave direction (θp) using ECMWF's Ocean Wave Model (WAM). The 10 km resolution ERA-40 reanalysis data allowed Semedo et al. (2015) to capture seasonal trends in swell and wind sea and the ≥ 10 cm per decade increase in winter Hs over the northern Atlantic. Stopa et al. (2016) used CFSR and altimetry data to calculate an average Hs of 1.5 m (99th percentile of 5–6 m) for the period 1992–2014 west of Svalbard. Wojtysiak et al. (2018) observed up to 1 m Hs difference between winter (higher) and summer (lower) months using WW3 (2005–2015; at 0.5∘ resolution) and ERA-Interim (1979–2015; at 1∘ resolution), and they found a statistically significant trend of increasing frequency (2 storms per decade) and total duration (4 d per decade) of storms for the Greenland Sea off south-western Svalbard for the 1979–2015 period, with the typical annual values of 10–40 storms and 20–80 d, respectively.
The large-scale models are good for understanding the general trends in the Arctic/Svalbard area but provide limited information on local-scale wave parameters in specific fjords and bays (Nederhoff et al., 2022). How the open ocean wave conditions translate into wave conditions in the coastal areas is poorly constrained given complex coastal wind patterns and bottom topography (Semedo et al., 2015). Moreover, the large-scale models oversimplify most aspects of wind wave–sea ice interactions. Most operational models use simple empirical formulae for wave attenuation in sea ice (Barnhart et al., 2014; Zhao et al., 2015; Ardhuin et al., 2016).
Herman et al. (2019) used three nested Simulating WAves Nearshore (SWAN; Booij et al., 1999) models to predict wind wave parameters within bays of Hornsund fjord (∼ 15 m depth), taking eastern Greenland Sea WW3 spectra as boundary conditions. They ran the model for two sea-ice-free 4-month periods (August–November 2015 and 2016), finding a good agreement between the modelled and measured significant wave height (r2 > 0.9) and mean absolute wave period (r2 = 0.63–0.78). The study added considerable detail to wind wave transformation in the nearshore environment of Hornsund by including fjord bathymetry, which allowed for resolving depth-induced wave breaking and bottom friction on wind conditions. Notably, the study used a subset of the dataset described in this paper to validate the wave spectral model (Herman et al., 2019).
The model of Herman et al. (2019) tested against buoy data performed well for ice-free conditions only. For a bay of the Beaufort Sea, Nederhoff et al. (2022) incorporated sea ice into the SWAN model, which enabled them to reliably describe wave climate in 1979–2019. The need for observational data to validate wave models, especially in periods when the sea ice is present, persists.
We present a 7.5-year (July 2013 to February 2021) wind wave dataset from Hornsund, southern Svalbard (77∘ N, 15.5∘ E). Our goal is to increase observational understanding of Arctic wave conditions by providing a dataset that can be further used to (i) analyse the inter- and intra-annual trends in nearshore wind wave conditions, (ii) calibrate and validate wave transformation models, (iii) quantify the role of sea ice in wave attenuation, (iv) create empirical models of wave run-up on high-latitude beaches, and (v) predict future wind wave conditions.
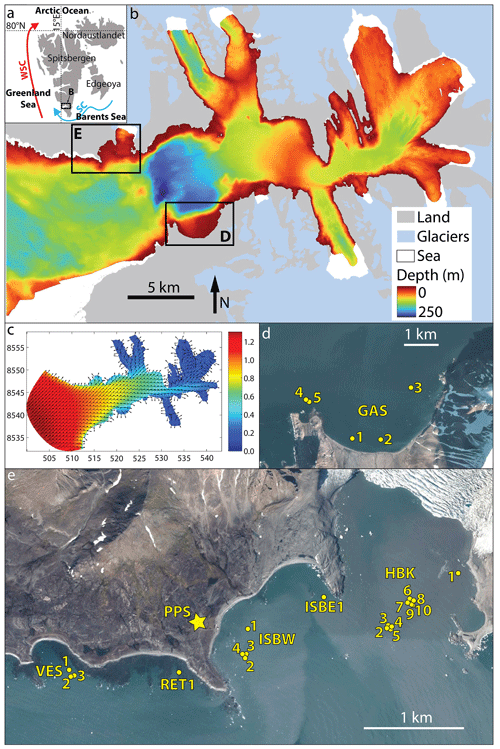
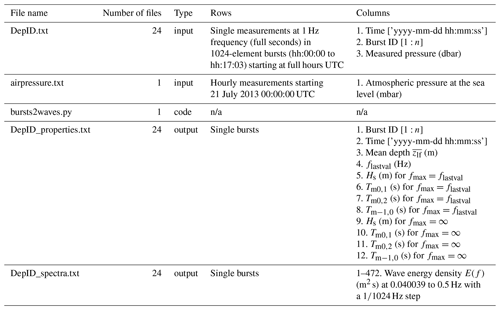
Figure 1Study area: (a) Svalbard archipelago; WSC = warm West Spitsbergen Current; SC = cold Sørkapp Current; (b) bathymetry of Hornsund fjord (source: Norwegian Hydrographic Service; permit granted to IG PAS); (c) mean significant wave height, Hs (colours, in metres, m) and wind wave direction, θp (arrows) from Herman et al. (2019); axis labels refer to Universal Transverse Mercator coordinate system zone 33X (UTM33X) coordinates (in kilometres, km); location of sensor deployments in southern (d) and northern (e) Hornsund. HBK = Hansbukta, ISB = Isbjørnhamna (W = western, E = eastern), RET = Rettkvalbogen, GAS = Gåshamna, VES = Veslebogen, PPS = Polish Polar Station. Background image © Norwegian Polar Institute (permit granted).
Hornsund is an ∼ 30 km long fjord of SW Spitsbergen, Svalbard (Fig. 1a). It has an ∼ 12 km wide and ∼ 100 m deep opening to the Greenland Sea. The average fjord depth is ∼ 100 m with the deeper (200–250 m) central part (Fig. 1b; Herman et al., 2019). The tides are semi-diurnal, and the average tidal range is 0.75 m (Kowalik et al., 2015). The circulation is cyclonic (anticlockwise) with the inflow from SW and outflow to the NW (Jakacki et al., 2017).
In 1979–2018 easterly winds dominated at the Polish Polar Station (12 ; PPS in Fig. 1e) with the mean direction of 124∘ (annual mean range of 102–140∘). Mean wind speed at ∼ 20 was 5.5 m s−1 (Wawrzyniak and Osuch, 2020).
Wave conditions in Hornsund are usually related to the long oceanic swell or mixed swell/wind sea from S–SW with short wind waves formed locally due to predominantly easterly winds. The mean Hs at the fjord mouth is 1.2–1.3 m, decreasing to 0.5–0.9 m in the central and to < 0.4 m in the inner parts of Hornsund (Fig. 1c). Northern shores of the fjord receive more wave energy than southern shores (Herman et al., 2019).
Hornsund bays (in this study Hansbukta, Isbjørnhamna, Rettkvalbogen, Veslebogen and Gåshamna) have complex shapes and bottom topography with ubiquitous skerries causing strong wave transformation due to refraction and dissipation (Herman et al., 2019).
Sea ice forms locally in the fjord or drifts from the open Greenland Sea. The latter originates east of Svalbard, drifts past the southern tip of Spitsbergen (Sørkapp) and then drifts northwards along the western Spitsbergen coast with cold Sørkapp Current (blue arrow in Fig. 1a). Fast ice (i.e. sea ice attached to the shore) persists during winter months. Muckenhuber et al. (2016) observed a decrease in sea-ice (both drift and fast ice) duration and extent between 2000 and 2014. In summer months glacier ice from calving tide-water glaciers (Błaszczyk et al., 2019) may accumulate in bays. Increased storminess coincident with positive air temperature anomalies and the lack of sea ice, in particular during October–December, may contribute to coastal erosion (Zagórski et al., 2015).
Table 1Details of the pressure sensor deployments for in situ wave measurements in Hornsund, Svalbard. Deployment ID (DepID) refers to bays: HBK = Hansbukta, ISB = Isbjørnhamna (W = western, E = eastern), RET = Rettkvalbogen, GAS = Gåshamna, VES = Veslebogen. LONGHORN ID refers to the IG PAS oceanographic monitoring (Swirad et al., 2022).
3.1 Input data
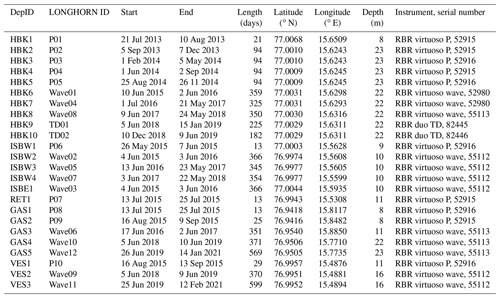
Pressure data were collected between 21 July 2013 and 12 February 2021 using RBR virtuoso P (continuous sampling at 4 or 6 Hz interval), RBR duo TD (continuous sampling at 1 Hz interval) and RBR virtuoso wave sensors (1024 s bursts at 30 min interval with 1 Hz sampling interval or at 60 min interval with 2 Hz sampling interval). There were 24 single deployments with a duration of 13–599 d (Table 1; Fig. 2). Initially the deployments were short ( < 100 d) and usually restricted to the fieldwork season (late spring to autumn). Since 2015, however, deployments were typically ∼ 1-year long with instrument recovery and redeployment during summer field campaigns. As a result of the COVID-19 pandemic, it was impossible to recover instruments in summer 2020, and the last two deployments (GAS5 and VES3) were > 550 d long and ended with the battery going dead.
The instruments were anchored to the seabed in various locations in northern (Hansbukta, western and eastern Isbjørnhamna, Rettkvalbogen, Veslebogen) and southern (Gåshamna) Hornsund (Fig. 1d and e). The raw pressure data are part of the LONGHORN oceanographic monitoring of the Institute of Geophysics, Polish Academy of Sciences, (IG PAS) and are provided in Swirad et al. (2022).
For consistency, the raw data were subsampled to 1024 s bursts at 60 min interval (starting at full hours) with 1 Hz sampling interval. The erroneous bursts at the start and end of deployments were removed. The datasets were cropped to full days so that the first measurement occurs at 00:00:00 UTC (hh:mm:ss) and the last one at 23:17:03 (1024 s after 23:00). These 24 deployment files are time series with three columns representing time, burst number and raw pressure (in dbar), and they are available as part of the dataset (Swirad et al., 2023).
3.2 Burst processing
The deployment files were imported into Spyder (Python 3.9) and processed on the burst-by-burst basis, with an algorithm described below (see also Wang et al., 1986; Karimpour and Chen, 2017; Marino et al., 2022, and references therein). Importantly, all steps described below are based on the linear wave theory; alternative data processing methods (e.g. Bonneton et al., 2018) might be applied to the original burst data to capture non-linear effects, but they are not considered here.
Hourly (one per burst) atmospheric pressure Pair (mbar) data at sea level were taken from the Polish Polar Station archive (https://monitoring-hornsund.igf.edu.pl/, last access: 28 March 2022). The water pressure, Psea (dbar), was calculated by subtracting atmospheric pressure from the raw pressure, Praw:
Figure 2Time span of pressure sensor deployments for in situ wave measurements in Hornsund, Svalbard. HBK = Hansbukta, ISB = Isbjørnhamna (W = western, E = eastern), RET = Rettkvalbogen, GAS = Gåshamna, VES = Veslebogen.
Depth, z (m), was calculated using the UNESCO formula (Fofonoff and Millard, 1983) under assumption of constant water temperature of 0 ∘ C, salinity of 35 PSU and latitude φ = 77∘ N:
where g (m s−2) denotes acceleration due to gravity, computed as
and x is given by
The slowly varying component of water depth (due to, for example, tide and storm surge) was removed by subtracting from z a least-square-fitted second-order polynomial trend, zlf, resulting in time series zhf (m), related to depth variability associated with wind waves: zhf = z−zlf. The energy density spectrum at depth z, Ez(f) (in m2 s), was computed by applying fast Fourier transform (FFT; Frigo and Johnson, 2005) to the time series zhf. As already mentioned, the data length used for FFT input was 1024. The Python fft function with default settings was used to compute the spectra, and no windowing was applied.
Finally, the spectrum at the sea surface, E0(f), was computed from Ez(f) by applying a correction factor A(f) accounting for the decrease of the wave orbital motion (and thus pressure fluctuations) with depth (compare red and blue spectra in Fig. 3):
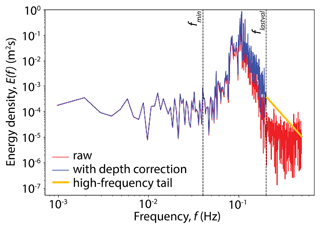
Figure 3An example of wave energy density spectrum computed with the algorithm described in the text (deployment HBK9 burst no. 1): raw spectrum Ez(f) at the depth of the logger (red), depth-corrected spectrum E0(f) (blue), and the analytical high-frequency tail (yellow). Frequency fmin = 0.04 Hz is the minimum frequency used to calculate mean wave parameters, and flastval is the highest frequency reliably measured. The plot is limited to f = 0.5 Hz, which is the upper limit of the observation data. Wave parameters are calculated in two versions: for fmin < f < flastval and for fmin < f < ∞.
To this end, a set K of basic wavenumber values was defined, K = (m−1), and a corresponding set of basic wave frequencies, F, with the following elements:
The set of correction factors A is then given by
where and denote the mean bottom depth and the mean logger depth, respectively (in the present case, with loggers mounted at the bottom, = ; averaging takes place over burst duration). The correction factor in Eq. (5) was calculated by linearly interpolating F and A to the frequencies of the energy spectrum. (Note that g in expression 6 was computed from Eqs. 3 and 4 without the last term in Eq. 3, i.e. for Psea=0.)

Figure 4An example of outputs for 1 month (July 2018) of deployment HBK9: (a) mean depth ; (b) primary y axis: significant wave height, Hs for fmax=∞, secondary y axis: the difference between Hs for fmax=∞ and for fmax=flastval; (c) wave period, T, for fmax=∞; (d) wave energy spectra E0(f).
As A(f) quickly decreases with increasing wave frequency, the values of E0(f) computed from Eq. (5) become unreliable for f higher than some limiting frequency flastval. Here, flastval was computed for each spectrum separately, based on a universal (constant for all spectra) limiting value of A: Alim=0.05 (note that, consistent with the linear wave theory used throughout this analysis, the values of A depend only on water depth and frequency of a given spectral component but not on the amplitude of that component). That is, flastval is the highest frequency for which A>Alim. For all f>flastval, a high-frequency tail of the form was added after Kaihatu et al. (2007) by extrapolating the trend from the last n=10 reliably estimated E0(f) values (yellow line in Fig. 3):
where
3.3 Mean wave parameters
In calculation of mean (integral) wave parameters, frequencies f<fmin = 0.04 Hz (corresponding to wave periods higher than 25 s) were ignored. This limit corresponds to the approximate boundary between wind-generated and infragravity waves, as well as to the lower-frequency limit typically used in spectral wave models (e.g. Holthuijsen, 2007). Thus, the mean wave parameters were computed for fmin < f < fmax. In the final dataset, two sets of those parameters are provided, referred to as observational one (for fmax = flastval) and modelled one (for fmax=∞). The spectral moments mn of E0(f) are defined as
where is computed from Eq. (9), C=0 if fmax = flastval and C=1 if fmax=∞. Based on mn, the following wave parameters are calculated: the significant wave height Hs, the mean absolute wave period Tm0,1, the mean absolute zero-crossing period Tm0,2, and the so-called energy period :
3.4 Output data
There are two output files for each deployment with rows representing bursts. The first one (“DepID_properties.txt”) contains the information on burst (number and time), mean water depth , and the four mean wave parameters defined in Eqs. (11)–(14), in two versions, i.e. for C=0 and C=1, respectively, in Eq. (10). The second file provides wave energy spectra for frequencies from 0.040039 to 0.5 Hz with step Δf = Hz (472 columns). Figure 4 provides a visualisation of an example 1-month period of data. Table 2 provides the dataset content (Swirad et al., 2023).
3.5 Quality control
The instruments remained at the seabed thanks to the anchor weight. However, a few times they were transported by ice or strong waves resulting in an abrupt change in mean depth visible in the output data (e.g. Fig. 5a). This situation occurred three times: in VES1 bursts no. 83 (depth rise of ∼ 1 m) and no. 370 (depth drop of ∼ 2.3 m) and in GAS5 burst no. 13 420 (depth rise of ∼ 0.7 m). In the case of VES1 burst no. 83 and GAS5 burst no. 13 420, it occurred in between bursts with no impact on calculated wave energy spectra and bulk parameters. Therefore, the data are left unchanged. If the dataset is used for tide analysis, time series should be split at the depth change event and treated separately. To identify erroneous bursts, we investigated the energy density for f < 0.5 Hz and identified two bursts with abnormally high energy density at low frequencies that resulted in erroneous calculation of bulk parameters (e.g. Fig. 5b): VES1 burst no. 370 and HBK1 burst no. 44. In the first case, the error resulted from instrument displacement during the burst. In the second case, mean depth rose by ∼ 0.5 m, remained higher for a few hours and dropped back to a typical level. There was no anomaly in atmospheric pressure and we speculate that the artefact may be due to the presence of glacier ice at the sea surface. In both cases, we replaced all output wave parameters with “NaN” (not a number).
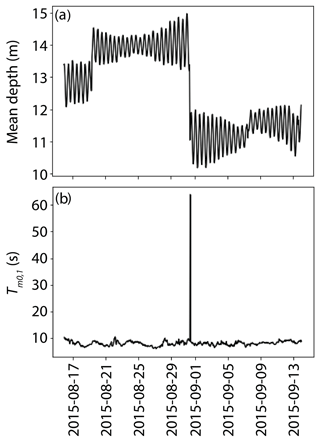
Figure 5An example of data errors for deployment VES1: (a) mean depth ; (b) mean wave period Tm0,1 for f < 0.5 Hz.

Figure 6Distribution of significant wave height, Hs (y axis; range: 0–4 m with 0.1 m bins) and mean absolute wave period, Tm0,1 (x axis; range 0–20 s with 0.1 s bins) with fmax=∞ for (a) Hansbukta (HBK), (b) western Isbjørnhamna (ISBW), (c) eastern Isbjørnhamna (ISBE), (d) Gåshamna (GAS), and (e) Veslebogen (VES).

Figure 7Summary of the wind wave characteristics for Hansbukta (HBK), Gåshamna (GAS) and Veslebogen (VES) for fmax=∞: (a) mean daily significant wave height, Hs, smoothed with a 15 d moving average; (b) mean daily significant wave height, Hs, for days of year smoothed with a 5 d moving average; (c) mean daily absolute wave period, Tm0,1, smoothed with a 15 d moving average; (d) mean daily absolute wave period, Tm0,1, for days of year smoothed with a 5 d moving average.
Table 3Summary of significant wave height (Hs: mean, 99th percentile for the full dataset and by quarters of the year) and mean full dataset wave period (mean absolute wave period Tm0,1, mean absolute zero-crossing period Tm0,2, and energy period ). HBK = Hansbukta, ISB = Isbjørnhamna (W = western, E = eastern), GAS = Gåshamna, VES = Veslebogen. Rettkvalbogen (RET) is excluded as the 13 d duration is not sufficient to derive seasonal statistics.

For all bays except Rettkvalbogen, time series length exceeded 1 year, providing information on seasonal variability in wind wave conditions. The largest waves characterise Veslebogen, the western-most of the analysed northern bays (Fig. 6). Mean full dataset Hs ranged from 0.25 m in eastern Isbjørnhamna to 0.43 m in Veslebogen, and respective 99th percentile Hs values equalled 1.21 and 1.96 m. Waves were the highest in the first and last quarters of the year with the highest mean Hs of 0.53 m in October–December and 99th percentile Hs of 2.32 m in January–March, both in Veslebogen (Table 3). A seasonal trend is also clearly visible in Fig. 7. Winter months are characterised by generally higher and longer waves, a finding consistent with the multi-decadal wave model reanalysis of Wojtysiak et al. (2018) for open Greenland Sea, west of Hornsund.
The inputs, outputs and the Python code described in this paper are available in the PANGAEA repository (https://doi.org/10.1594/PANGAEA.954020; Swirad et al., 2023). Raw data downloaded from the instruments are part of the IG PAS LONGHORN oceanographic monitoring, and they are available at the IG PAS Data Portal (https://doi.org/10.25171/InstGeoph_PAS_IGData_NBP_2022_005; Swirad et al., 2022). As the monitoring programme is on-going, future raw data and data processed in the same way as described here will be uploaded to the IG PAS Data Portal (https://dataportal.igf.edu.pl/, last access: 26 June 2023).
We present the first multi-year continuous wind wave and water level dataset for Hornsund fjord, Svalbard. Twenty four single deployments of underwater RBR sensors at 8–23 m depth between July 2013 and February 2021 were used to measure water levels in five bays of northern Hornsund (Hansbukta, western Isbjørnhamna, eastern Isbjørnhamna, Rettkvalbogen, Veslebogen) and one of southern (Gåshamna) Hornsund. Raw data (Swirad et al., 2022) were subsampled to 1024 s sets (∼ bursts) at 1 Hz measurement interval at 1 h burst interval, and they were then used to derive mean water levels, wave spectra and bulk wave parameters. We describe the procedure (available also as a Python code) that includes subtracting atmospheric pressure, depth calculation, fast Fourier transform, correction for the decrease of the wave orbital motion with depth and adding a high-frequency tail. We performed quality control on the output data. The dataset can be used to, for example, characterise wind wave climate in Hornsund; identify seasonal to inter-annual trends; calibrate and validate wave models (as shown by Herman et al., 2019); and facilitate analysis of sea-ice impact on wave attenuation, empirical modelling of wave run-up on Arctic beaches, and predicting future change. We provide individual bursts with pressure time series and the code for the users to apply different analysis methods, use alternative algorithm parameters, analyse non-linear effects, etc., depending on the application.
MM initiated and maintains the oceanographic monitoring in Hornsund. ZMS secured the funding. ZMS wrote the code and processed the data with support from AH and MM. All authors wrote the paper.
The contact author has declared that none of the authors has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We thank Kacper Wojtysiak for sharing his MATLAB code, Aleksandra Stępień and Adam Słucki (HańczaTECH) for helping in the underwater work, and the Polar Polish Station crew for maintaining the oceanographic and meteorological monitoring. We are grateful to Tsubasa Kodaira and an anonymous reviewer for constructive comments.
This study was funded by the National Science Centre of Poland (grant no. 2021/40/C/ST10/00146). Acquisition of raw data (Swirad et al., 2022) was funded by the National Science Centre of Poland (grant no. 2013/09/B/ST10/04141) and IG PAS LONGHORN oceanographic monitoring in collaboration with Polish Polar Station Hornsund and the Ministry of Education and Science of Poland (statutory activities no. 3841/E-41/S/2022).
This paper was edited by Giuseppe M.R. Manzella and reviewed by Tsubasa Kodaira and one anonymous referee.
Ardhuin, F., Sutherland, P., Doble, M., and Wadhams, P.: Ocean waves across the Arctic: attenuation due to dissipation dominates over scattering for periods longer than 19 s: observed ocean wave attenuation across the arctic, Geophys. Res. Lett., 43, 5775–5783, https://doi.org/10.1002/2016GL068204, 2016.
Barnhart, K. R., Overeem, I., and Anderson, R. S.: The effect of changing sea ice on the physical vulnerability of Arctic coasts, The Cryosphere, 8, 1777–1799, https://doi.org/10.5194/tc-8-1777-2014, 2014.
Błaszczyk, M., Ignatiuk, D., Uszczyk, A., Cielecka-Nowak, K., Grabiec, M., Jania, J. A., Moskalik, M., and Walczowski, W.: Freshwater input to the Arctic fjord Hornsund (Svalbard), Polar Res., 38, 3506, https://doi.org/10.33265/polar.v38.3506, 2019.
Bonneton, P., Lannes, D., Martins, K, and Michallet, H.: A nonlinear weakly dispersive method for recovering the elevation of irrotational surface waves from pressure measurements, Coast. Eng. 138, 1–8, https://doi.org/10.1016/j.coastaleng.2018.04.005, 2018.
Booij, N., Ris, R. C., and Holthuijsen, L. H.: A third-generation wave model for coastal regions. 1. Model description and validation, J. Geophys. Res., 104, 7649–7666, https://doi.org/10.1029/98jc02622, 1999.
Carrasco, A., Saetra, Ø., Burud, A., Müller, M., and Melsom A.: Product user manual for Arctic Ocean Wave Analysis and Forecasting products ARCTIC_ANALYSIS_FORECAST_WAV_002_014, Issue: 1.6, Copernicus Marine Service, https://doi.org/10.48670/moi-00002, 2022.
Dee, D. P., Uppala, S. M., Simmons, A. J., Berrisford, P., Poli, P., Kobayashi, S., Andrae, U., Balmaseda, M. A., Balsamo, G., Bauer, P., Bechtold, P., Beljaars, A. C. M., van de Berg, L., Bidlot, J., Bormann, N., Delsol, C., Dragani, R., Fuentes, M., Geer, A. J., Haimberger, L., Healy, S. B., Hersbach, H., Hólm, E. V., Isaksen, L., Kållberg, P., Köhler, M., Matricardi, M., McNally, A. P., Monge-Sanz, B. M., Morcrette, J.-J., Park, B.-K., Peubey, C., de Rosnay, P., Tavolato, C., Thépaut, J.-N., and Vitart, F.: The ERA-Interim reanalysis: configuration and performance of the data assimilation system, Q. J. Roy. Meteor. Soc., 137, 553–597, https://doi.org/10.1002/qj.828, 2011.
Fofonoff, N. P. and Millard Jr., R. C.: Algorithms for computation of fundamental properties of seawater, UNESCO Technical Papers in Marine Science, 44, https://darchive.mblwhoilibrary.org/bitstream/handle/1912/2470/059832eb.pdf (last access: 28 November 2022), 1983.
Forbes, D.: State of the Arctic Coast 2010 – Scientific Review and Outlook, Tech. Rep., International Arctic Science Committee, Land-ocean Interactions in the Coastal Zone, Arctic Monitoring and Assessment Programme, International Permafrost Association, Helmholtz-Zentrum, Geesthacht, Germany, 178 pp., http://arcticcoasts.org (last access: 28 November 2022), 2011.
Francis, O. P., Panteleev, G. G., and Atkinson, D. E.: Ocean wave conditions in the Chukchi Sea from satellite and in situ observations, Geophys. Res. Lett., 38, L24610, https://doi.org/10.1029/2011GL049839, 2011.
Frigo, M. and Johnson, S. G.: The Design and Implementation of FFTW3, P. IEEE, 93, 216–231, https://doi.org/10.1109/JPROC.2004.840301, 2005.
Herman, A., Wojtysiak, K., and Moskalik, M.: Wind wave variability in Hornsund fjord, west Spitsbergen, Estuar. Coast. Shelf S., 217, 96–109, https://doi.org/10.1016/j.ecss.2018.11.001, 2019.
Hersbach, H., Bell, B., Berrisford, P., Hirahara, S., Horányi, A., Muñoz-Sabater, J., Nicolas, J., Peubey, C., Radu, R., Schepers, D., Simmons, A., Soci, C., Abdalla, S., Abellan, X., Balsamo, G., Bechtold, P., Biavati, G., Bidlot, J., Bonavita, M., De Chiara, G., Dahlgren, P., Dee, D., Diamantakis, M., Dragani, R., Flemming, J., Forbes, R., Fuentes, M., Geer, A., Haimberger, L., Healy, S., Hogan, R. J., Hólm, E., Janisková, M., Keeley, S., Laloyaux, P., Lopez, P., Lupu, C., Radnoti, G., de Rosnay, P., Rozum, I., Vamborg, F., Villaume, S., and Thépaut, J. N.: The ERA5 global reanalysis. Q. J. Roy. Meteor. Soc., 1–51, https://doi.org/10.1002/qj.3803, 2020.
Holthuijsen, L.: Waves in Oceanic and Coastal Waters, Cambridge University Press, https://doi.org/10.1017/CBO9780511618536, 387 pp., 2007.
IPCC: The Ocean and Cryosphere in a Changing Climate, International Panel on Climate Change, https://www.ipcc.ch/srocc/home (last access: 28 November 2022), 2019.
Jakacki, J., Przyborska, A., Kosecki, S., Sundfjord, A., and Albretsen, J.: Modelling of the Svalbard fjord Hornsund, Oceanologia, 59, 473–495, https://doi.org/10.1016/j.oceano.2017.04.004, 2017.
Kaihatu, J., Veeramony, J., Edwards, K., and Kirby, J.: Asymptotic behaviour of frequency and wave number spectra of nearshore shoaling and breaking waves, J. Geophys. Res., 112, C06016, https://doi.org/10.1029/2006JC003817, 2007.
Karimpour, A. and Chen, Q.: Wind wave analysis in depth limited water using OCEANLYZ, A MATLAB toolbox, Comput. Geosci. 106, 181–189, https://doi.org/10.1016/j.cageo.2017.06.010, 2017.
Kowalik, Z., Marchenko, A., Brazhnikov, D., and Marchenko, N.: Tidal currents in the western svalbard fjords, Oceanologia, 57, 318–327, https://doi.org/10.1016/j.oceano.2015.06.003, 2015.
Marino, M., Rabionet, I. C., and Musumeci, R. E.: Measuring free surface elevation of shoaling waves with pressure transducers, Cont. Shelf Res., 245, 104803, https://doi.org/10.1016/j.csr.2022.104803, 2022.
Muckenhuber, S., Nilsen, F., Korosov, A., and Sandven, S.: Sea ice cover in Isfjorden and Hornsund, Svalbard (2000–2014) from remote sensing data, The Cryosphere, 10, 149–158, https://doi.org/10.5194/tc-10-149-2016, 2016.
Nederhoff, K., Erikson, L., Engelstad, A., Bieniek, P., and Kasper, J.: The effect of changing sea ice on wave climate trends along Alaska's central Beaufort Sea coast, The Cryosphere, 16, 1609–1629, https://doi.org/10.5194/tc-16-1609-2022, 2022.
Reistad, M., Breivik, Ø., Haakenstad, H., Aarnes, O. J., Furevik, B. R., and Bidlot, J.-R.: A high-resolution hindcast of wind and waves for the North Sea, the Norwegian Sea, and the Barents Sea. J. Geophys. Res., 116, C05019, https://doi.org/10.1029/2010JC006402, 2011.
Saha, S., Moorthi, S., Wu, X., Wang, J., Nadiga, S., Tripp, P., Behringer, D., Hou, Y.-T., Chuang, H.-Y., Iredell, M., Ek, M., Meng, J., Yang, R., Mendez, M. P., van den Dool, H., Zhang, Q., Wang, W., Chen, M., and Becker, E.: The NCEP Climate Forecast System Version 2, J. Climate, 27, 2185–2208, https://doi.org/10.1175/jcli-d-12-00823.1, 2014.
Semedo, A., Vettor, R., Breivik, Ø., Sterl, A., Reistad, M., Guedes Soares, C., and Lima, D.: The wind sea and swell waves climate in the Nordic seas, Ocean Dynam., 65, 223–240, https://doi.org/10.1007/s10236-014-0788-4, 2015.
Stopa, J. E., Ardhuin, F., and Girard-Ardhuin, F.: Wave climate in the Arctic 1992–2014: seasonality and trends, The Cryosphere, 10, 1605–1629, https://doi.org/10.5194/tc-10-1605-2016, 2016.
Swirad, Z. M., Moskalik, M., and Glowacki, O.: Sea pressure and wave monitoring datasets in Hornsund fjord, IG PAS Data Portal [data set], https://doi.org/10.25171/InstGeoph_PAS_IGData_NBP_2022_005, 2022.
Swirad, Z. M., Moskalik, M., and Herman, A.: In situ wind wave and water level measurements in Hornsund, Svalbard in 2013–2021, PANGAEA [data set], https://doi.org/10.1594/PANGAEA.954020, 2023.
Uppala, S. M., Kållberg, P. W., Simmons, A. J., Andrae, U., Da Costa Bechtold, V., Fiorino, M., J. K. Gibson, J. K., Haseler, J., Hernandez, A., Kelly, G. A., Li, X., Onogi, K., Saarinen, S., Sokka, N., Allan, R. P., Andersson, E., Arpe, K., Balmaseda, M. A., Beljaars, A. C. M., Van De Berg, L., Bidlot, J., Bormann, N., Caires, S., Chevallier, F., Dethof, A., Dragosavac, M. Fisher, M. Fuentes, M., Hagemann, S., Hólm, E., Hoskins, B. J., Isaksen, L., Janssen, P. A. E. M., Jenne, R., Mcnally, A. P., Mahfouf, J.-F., Morcrette, J.-J., Rayner, N. A., Saunders, R. W. Simon, P., Sterl, A., Trenberth, K. E., Untch, A. Vasiljevic, D., Viterbo, P., and Woollen J.: The ERA40 reanalysis, Q. J. Roy. Meteor. Soc., 131, 2961–3012, https://doi.org/10.1256/qj.04.176, 2005.
Wang, H., Lee, D.-Y., and Garcia, A.: Time series surface-wave recovery from pressure gage, Coast. Eng., 10, 379–393, https://doi.org/10.1016/0378-3839(86)90022-0, 1986.
Wang, X. L., Feng, Y., Swail, V. R., and Cox, A.: Historical changes in the Beaufort–Chukchi–Bering seas surface winds and waves, 1971–2013, J. Climate, 28, 7457–7469, https://doi.org/10.1175/JCLI-D-15-0190.1, 2015.
Waseda, T., Webb, A., Sato, K., Inoue, J., Kohout, A., Penrose, B., and Penrose, S.: Correlated increase of high ocean waves and winds in the ice-free waters of the Arctic Ocean, Sci. Rep., 8, 4489, https://doi.org/10.1038/s41598-018-22500-9, 2018.
Wawrzyniak, T. and Osuch, M.: A 40-year High Arctic climatological dataset of the Polish Polar Station Hornsund (SW Spitsbergen, Svalbard), Earth Syst. Sci. Data, 12, 805–815, https://doi.org/10.5194/essd-12-805-2020, 2020.
Wojtysiak, K., Herman, A., and Moskalik, M.: Wind wave climate of west Spitsbergen: seasonal variability and extreme events, Oceanologia, 60, 331–343, https://doi.org/10.1016/j.oceano.2018.01.002, 2018.
WW3DG: User manual and system documentation of WAVEWATCH III R version 6.07, Tech. Note 333, The WAVEWATCH III R Development Group, NOAA/NWS/NCEP/MMAB, College Park, MD, USA, 465 pp. + Appendices, https://github.com/NOAA-EMC/WW3/wiki/files/manual.pdf (last access: 28 November 2022), 2019.
Zagórski, P., Rodzik, J., Moskalik, M., Strzelecki, M. C., Lim, M., Błaszczyk, M., Promińska, A., Kruszewski, G., Styszyńska, A., and Malczewski, A.: Multidecadal (1960–2011) shoreline changes in Isbjørnhamna (Hornsund, Svalbard), Pol. Polar Res., 36, 369–390, 2015.
Zhao, X., Shen, H. H., and Cheng, S.: Modeling ocean wave propagation under sea ice covers, Acta Mech. Sinica Xuebao, 31, 1–15, https://doi.org/10.1007/s10409-015-0017-5, 2015.