the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
One hundred plus years of recomputed surface wave magnitude of shallow global earthquakes
Dmitry A. Storchak
Among the multitude of magnitude scales developed to measure the size of an earthquake, the surface wave magnitude Ms is the only magnitude type that can be computed since the dawn of modern observational seismology (beginning of the 20th century) for most shallow earthquakes worldwide. This is possible thanks to the work of station operators, analysts and researchers that performed measurements of surface wave amplitudes and periods on analogue instruments well before the development of recent digital seismological practice. As a result of a monumental undertaking to digitize such pre-1971 measurements from printed bulletins and integrate them in parametric data form into the database of the International Seismological Centre (ISC, http://www.isc.ac.uk, last access: August 2021), we are able to recompute Ms using a large set of stations and obtain it for the first time for several hundred earthquakes. We summarize the work started at the ISC in 2010 which aims to provide the seismological and broader geoscience community with a revised Ms dataset (i.e., catalogue as well as the underlying station data) starting from December 1904 up to the last complete year reviewed by the ISC (currently 2018). This Ms dataset is available at the ISC Dataset Repository at https://doi.org/10.31905/0N4HOS2D (International Seismological Centre, 2021d).
- Article
(4580 KB) - Full-text XML
- BibTeX
- EndNote
Since its introduction, the surface wave magnitude Ms has been very popular, and for a long period of time, before the moment magnitude Mw was introduced by Kanamori (1977) and Hanks and Kanamori (1979), it was considered the most reliable magnitude to estimate an earthquake size. Its popularity originated due to the following: (a) as opposed to the magnitude concept introduced at a local scale by Richter (1935), Ms allows seismologists to compute magnitudes for earthquakes worldwide, including those recorded at teleseismic distances (i.e., from 20∘ onward), without relying on local recordings that were not available in most seismic zones; (b) thanks to the work of station operators, analysts and researchers at various observatories around the world that produced readings of surface wave data for shallow earthquakes since the beginning of the last century, Ms can be computed (systematically) since the dawn of instrumental seismology (Fig. 1). In addition, Ms is probably the only type of earthquake magnitude that can be computed systematically for all damaging earthquakes for the last 100+ years. However, as any magnitude type Ms also has shortcomings, such as the possible underestimation for some large earthquake (as discussed later), the inability of processing surface waves from short-period instruments (hence for many small local earthquakes) and the limitation, at least in standard procedures (IASPEI, 2013), of being defined for shallow earthquakes.
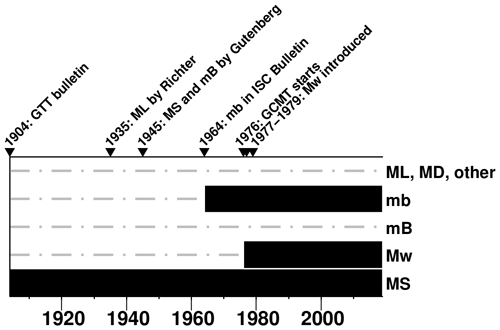
Figure 1Availability over time of common magnitude scales for worldwide (Ms, Mw, broad-band and short-period body-wave magnitude mB and mb, respectively) and local/regional (e.g., Richter and duration magnitude Ml and Md, respectively) earthquakes. Solid thick black lines represent time periods over which a magnitude scale is available or can be recomputed systematically (dashed–dotted thin grey lines otherwise). For local/regional magnitudes the availability only regards limited continental areas (Di Giacomo and Storchak, 2016). Listed on top are some significant developments in terms of earthquake magnitude. Among those GTT refers one of the first printed station bulletins produced at the Göettingen observatory in Germany (Schering, 1905), which pioneered modern observational seismological practice, and GCMT is the Global Centroid Moment Tensor project (https://www.globalcmt.org, last access: August 2021, Dziewonski et al., 1981; Ekström et al., 2012).
Gutenberg (1945), using measurements of amplitudes and periods of surface waves accumulated during the first 40 years of the last century, introduced Ms as
Since then a team of researchers from Moscow and Prague further developed Gutenberg's work and proposed the formula (Kárník et al., 1962; Vanĕk et al., 1962)
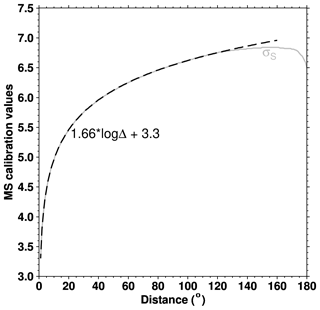
where A and T are the amplitude (in µm) and period (in s) of the surface wave train, respectively, and Δ is the distance in degrees of the seismic station from the earthquake epicentre (distance and period limits will be discussed in the next section). This is the so-called Moscow–Prague formula, and it was accepted as the standard for Ms computation by the International Association of Seismology and Physics of the Earth's Interior (IASPEI, http://www.iaspei.org/, last access: August 2021) at the 1967 Zurich meeting (Bormann et al., 2012; IASPEI, 2013). The calibration function σS(Δ) and its best fit up to 160∘ (1.66log Δ+3.3) are shown in Fig. 2.
Several earthquake catalogues that listed Ms have served the seismological community for various purposes in the past decades. One that has been instrumental for many studies is Abe's catalogue (Abe, 1981; Abe and Noguchi, 1983a, b; Abe, 1984). This catalogue lists Ms values for large earthquakes (mostly Ms>6.5) up to 1980, and its reliability was recently confirmed by Di Giacomo et al. (2015a). Since then researchers have extend Abe's catalogue beyond 1980 with Ms solutions from the International Seismological Centre (ISC, http://www.isc.ac.uk, last access: August 2021) and/or the National Earthquake Information Center of the USGS (https://earthquake.usgs.gov/earthquakes/search/, last access: August 2021). Such a composite Ms catalogue was then used as the magnitude basis for recent compilations such as the Centennial Catalogue (Engdahl and Villaseñor, 2002) and PAGER-CAT (Allen et al., 2009) as well as various types of research, from calibration purposes (Herak and Herak, 1993; Rezapour and Pearce, 1998) to patterns of the Earth's seismicity (e.g., Pérez and Scholz, 1984; Ogata and Abe, 1991; Pacheco and Sykes, 1992; Pérez, 1999).
Considering the important legacy of Ms in the seismological community, here we present a revised Ms catalogue (cut-off magnitude of 4.5) listing over 46 000 earthquakes as well as the underlying station data (files described in Sect. 7) used to derive Ms for each earthquake. Hereafter we refer to the catalogue and underlying station data as the ISC Ms dataset (International Seismological Centre, 2021d). To create this product we benefit from the work done by Di Giacomo et al. (2015b, 2018) to digitize (i.e., converted from printed to computer accessible format) a large volume of surface wave parametric data prior to 1971 and by Storchak et al. (2017, 2020) to rebuild the ISC Bulletin from 1964 onwards.
We first recall the basic steps in our procedure to compute Ms and outline the major features of the station data behind the calculation of the network Ms. Then we discuss some properties of the ISC Ms dataset in terms of completeness and rates in different time periods. Finally, we briefly discuss the largest earthquakes ever recorded and outline further activities that could improve this dataset in different time periods.
A big part of the ISC mission consists of collecting and reprocessing reports from seismological agencies all over the world to produce the ISC Bulletin (International Seismological Centre, 2021c). Details about agencies contributing data to the ISC can be found at http://www.isc.ac.uk/iscbulletin//agencies/ (last access: August 2021). The summary of the agencies (hereafter also referred to as reporters or data contributors) that contributed surface wave parametric data to create the ISC Ms dataset is shown in Fig. 3. A few aspects are worth mentioning regarding the surface wave data reporters.
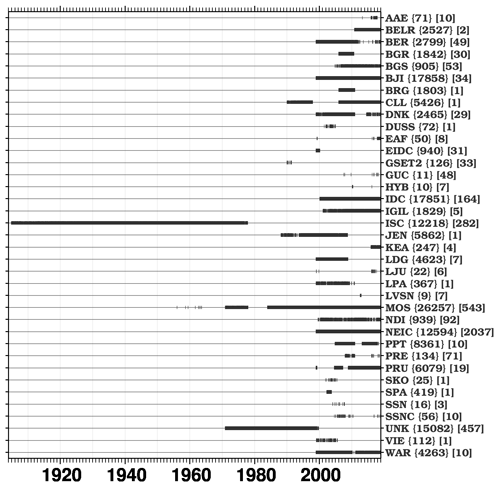
Figure 3Timelines of the agencies contributing with surface wave data (amplitude and period measurements). Each symbol represents the origin time of an earthquake. Details about each agency code can be found by typing the agency code at http://www.isc.ac.uk/iscbulletin//agencies/ (last access: August 2021). The total number of earthquakes and stations for each agency are listed in curly and square brackets, respectively. Note that a reporter that is UNK (unknown) is not a genuine reporter code, but it simply represents data collected before the ISC database was set up, i.e., when the association between data and reporter was not maintained.
Originally, the ISC had no surface wave data available in digital form for pre-1971 earthquakes. Hence, to fill this data gap, an onerous undertaking of digitizing surface wave data from station/network printed bulletins began in 2010 (Di Giacomo et al., 2015b, 2018). As shown in Fig. 3, this effort resulted in the ISC having digitized surface wave data from a total of 282 stations for over 12 000 earthquakes (it is our intention to continue this effort; see Sect. 6).
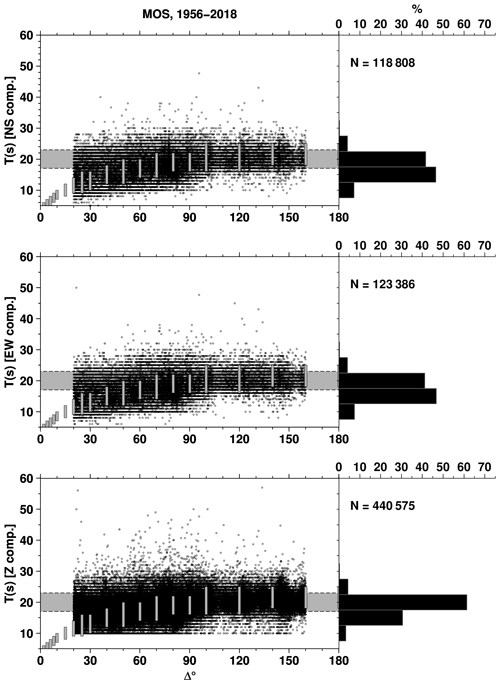
Between 1971 and 1998 the ISC Bulletin contains surface wave data from 457 stations worldwide. However, in this time period we cannot associate such data to specific reporters (hence reporter is UNK, unknown, in Fig. 3). The only exceptions to that are data reports (e.g., agency MOS, JEN, CLL) parsed in the ISC Bulletin during the Rebuild project (Storchak et al., 2017, 2020). Since 1999, coinciding with a major update in ISC data collection procedures and the setup of the ISC database, we are able to routinely associate station data with their agency. Only 30 reporters out of about 150 contributed surface wave data in the last 20 years, with the largest contributors being IDC, NEIC, MOS and BJI (Fig. 3).
Our approach to computing Ms closely follows the standard ISC procedure (Bondár and Storchak, 2011) and is already detailed in Di Giacomo et al. (2015a). However, it is beneficial here to (1) recall some aspects of the procedure in light of the content of station data files (Sect. 7) and (2) explain some necessary deviations from it.
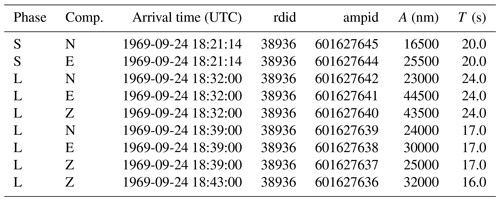
First, we consider the surface wave data belonging to a reading (in ISC jargon a reading groups all parametric data from a single station associated to a specific seismic event and reported by the same agency). A reading can have any number of surface wave data entries, and different reporters may provide a reading for the same station. An example of a reading is shown in Table 1 for station CLL (Collm, Germany) for an earthquake which occurred in the northern Mid-Atlantic Ridge, 24 September 1969. We have chosen this example as the reading lists multiple surface wave data entries on all three components. Within the surface wave phases of the reading (L in our example), we first search for the maximum of on the vertical component, and, if available, the component magnitude MsZ is obtained via the Moscow–Prague formula. Then, for periods within ±10 s of T on the vertical component, the maximum of for the horizontal vector component
is searched to calculate the component MsH magnitude. If one of the two horizontal components is not available then
Although our procedure finds the maximum of within the reading, a reporter may have provided single component measurements of . In our CLL reading example the maximum on the vertical component is defined by ampid equal to 601627636, whereas ampid equal to 601627639 and 601627638 on the north–south and east–west component, respectively, defines the maximum horizontal vector component. Such defining entries are included in the station data files (more details in International Seismological Centre, 2021d). Then the Ms for the reading is computed as if both exists, or if one of them is not available. If more than one reading Ms exists for a station, the median of the readings Ms is used as station Ms. Finally, the network Ms is computed as the median of the stations Ms if at least three or five station magnitudes are available prior to or since 1971, respectively. The uncertainty of the network Ms is expressed as the standard median absolute deviation (SMAD) of the α-trimmed station magnitudes (α=20 %).
Table 1Reading example from station CLL (Collm, Germany) associated to an event in the northern Mid-Atlantic Ridge that occurred on 24 September 1969 (). The surface wave measurements (L phases) are used by our procedure to obtain the reading Ms. The database identifiers for the reading and single amplitude-period entries, respectively, are rdid and ampid. See text for details.
In line with IASPEI recommendations (IASPEI, 2013), we only allow Ms for earthquakes with depth ≤ 60 km. The locations adopted in this work come from the ISC-GEM Catalogue (Bondár et al., 2015; Di Giacomo et al., 2018) between 1904 and 1963 and the rebuilt ISC Bulletin (Storchak et al., 2017, 2020) from 1964 onward.
Standard procedures at the ISC consider surface wave periods between 10 and 60 s and distances between 20 and 160∘. Such delta-period ranges are also adopted here for earthquakes which occurred after 1963 (hereafter also referred to as standard delta-period ranges). Prior to 1964 we expand the period and distance ranges to 5–60 s and 2–180∘, respectively, as discussed in Di Giacomo et al. (2015b). The augmentation of the delta-period limits prior to 1964 is mainly due to the relative scarcity of surface wave data in the first part of the last century compared to its second half (hence the need for not discarding station Ms) and to changes in seismological practice in many institutes coinciding with the introduction of the World-Wide Standardized Seismograph Network (WWSSN, Oliver and Murphy, 1971; Peterson and Hutt, 2014). When stations beyond 160∘ are used we use the tabulated values of σS(Δ) instead of its best fit (Fig. 2), as recommended by Bormann et al. (2012). In the next section we show that the amplitude/period measurements prior to the WWSSN introduction justify our delta-period expansion for pre-1964 earthquakes.
The decadal spatial distribution of the stations contributing to the ISC Ms dataset is summarized in Figs. 4–5. At times we mention seismic stations that, for sake of brevity, we may only identify by their code (station's full details can be accessed at International Seismological Centre, 2021b).
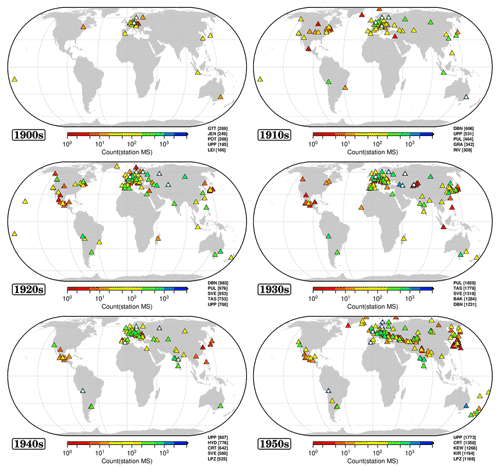
Figure 4Decadal (up to the 1950s) distribution of the stations (triangles) that contributed with surface wave data. Symbols are colour-coded by number of station Ms. For each decade, the top five stations in terms of Count(station Ms) are identified by a white circle and listed in the bottom-right corner outside each map. Maps drawn using the Generic Mapping Tools (GMT) (Wessel et al., 2013) software. Plots of the annual station Ms distributions are included in International Seismological Centre (2021d).
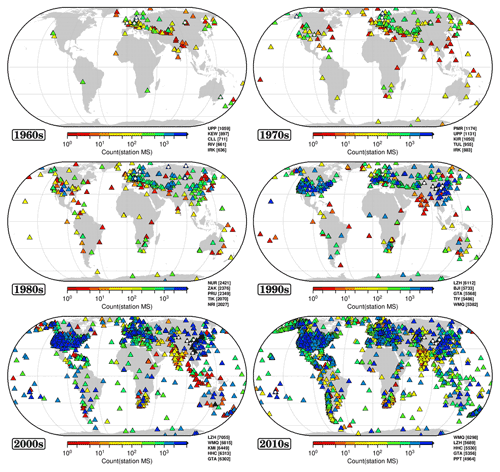
Figure 5As for Fig. 4 but since the 1960s. Maps drawn using the Generic Mapping Tools (GMT) (Wessel et al., 2013) software.
Not surprisingly, the Ms network geometry is unbalanced as the Northern Hemisphere features many more stations than the Southern Hemisphere (a known issue in every aspect of instrumental seismology). In more detail, these figures highlight how the Ms network became more dense and widespread over time after most of the stations were located in Europe at the beginning of the last century. Indeed, most of the Ms measurements in the first two decades of the last century heavily rely on stations in Germany (e.g., GTT, JEN), UPP in Sweden and a few others (e.g., DBN in the Netherlands and PUL in Russia). From the 1920s to the 1960s the station density increased in Europe and in former Soviet Union territory. North American stations also contributed but for a small number of earthquakes.
The Southern Hemisphere had only a handful of Ms reporting stations up to the 1970s–1980s. However, thanks to the extraordinary efficiency in observatory practice at the Observatorio San Calixto (LPZ, Bolivia, opened in 1913, Coenraads, 1993) and Riverview (RIV, Australia, opened in 1909, Drake, 1993), both from the Jesuit network (Udias and Stauder, 1996), our capabilities of obtaining Ms improved significantly in the first half of last century both for Southern Hemisphere and worldwide earthquakes, as was noted by Gutenberg and Richter (1954).
From the 1970s, when surface wave data started to be digitally available in the ISC Bulletin, we witness a significant increase in the Ms network coverage, particularly in the last two decades, where many more stations in the Southern Hemisphere have contributed to Ms. However, their spatial distribution is not yet as dense as in North America or the Euro-Mediterranean area.
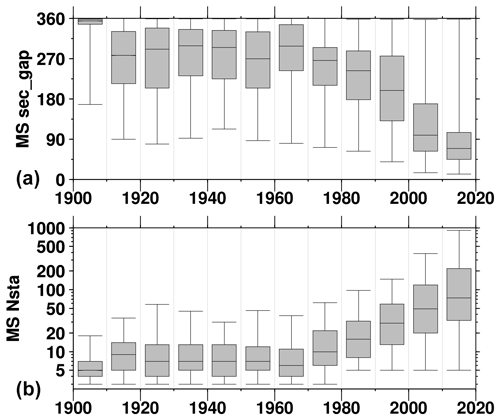
To summarize the evolution of the Ms network over the decades, Fig. 6 shows the network Ms decadal box-and-whisker plot of the number of stations (Nsta) and secondary gap (i.e., the largest azimuthal gap in which only one station exists, and the quality of the data at that station may bias the solution). The latter parameter is normally used as a network geometry parameter in earthquake location (Bondár et al., 2004), but here it is used as a measure of the azimuthal coverage of the station contributing to Ms computation (both gap and secondary gap are included in the Ms catalogue file). Ideally, the station distribution should sample the focal sphere from different azimuth to reduce the effects of propagation path heterogeneities and radiation pattern (von Seggern, 1970) on the network Ms, although the latter is symmetric for surface waves (either two-lobed or four-lobed). In light of the station distributions shown in Figs. 4–5, it is not surprising that for most of the last century the secondary gap is usually 180–270∘ or above, meaning that the stations contributing to the network Ms are often located in a narrow azimuth. To showcase the possible effects of this aspect, in Fig. A1 we show the azimuthal distribution of the station Ms for the 20 March 1960 earthquake off the east coast of Honshu (event 878564). Most of the Ms stations are located in Europe, and it appears that those are responsible for making the network Ms=7.9, as most of the station magnitudes at different azimuth are well below the final network Ms. Nevertheless, significant improvements in the station azimuthal coverage occur from the 1970s, and with the increase in Nsta we observe an overall decrease in secondary gap.
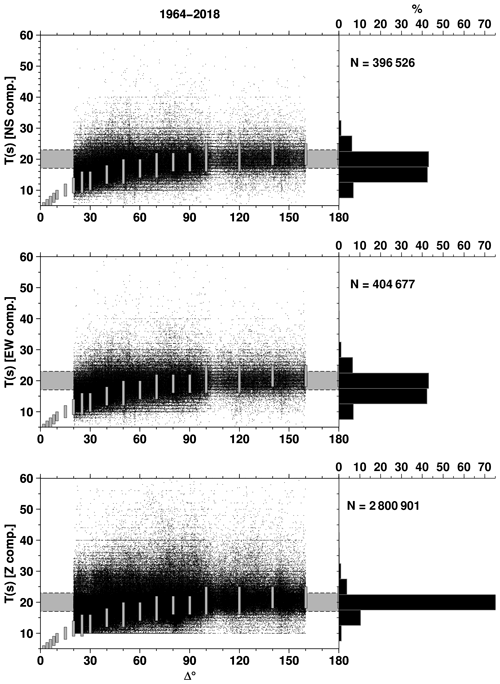
The final aspect of the station data we discuss here regards the period at which the amplitudes of the surface waves are measured. We do that by showing, similarly to Bormann et al. (2009, 2012), the distance-period distributions of for earthquakes prior to and since 1964 (Fig. 7 and Fig. 8, respectively). The separation in these two time periods is linked both to the start of the original ISC Bulletin (Adams et al., 1982) in 1964 and a change in observatory practice by many institutions due to the WWSSN introduction in the early 1960s. The standard WWSSN practice produces amplitudes of surface waves as measured for T around 20 s (usually ±2 or ±3 s) for distances ≥ 20∘ (in addition, measurements on the vertical component were preferred to horizontal ones since the 1970s). Before WWSSN, however, the standard practice was to measure the surface wave amplitudes in broader period ranges (such differences led IASPEI, 2013, to recommend the computation of two types of Ms, Ms20 and MsBB). Therefore, before 1964 we observe in Fig. 7 that T falls reasonably well within the expected period ranges of Vanĕk et al. (1962) (i.e., amplitudes measured over a broad T range and using data below 20∘), whereas from 1964 onward we see surface amplitudes predominantly measured around T of 20 s throughout the entire distance range, as shown by the vertical component of Fig. 8. The surface wave amplitude-period measurements pre-WWSSN, therefore, allow us to expand the delta-period limits for pre-1964 earthquakes as outlined in Sect. 2.
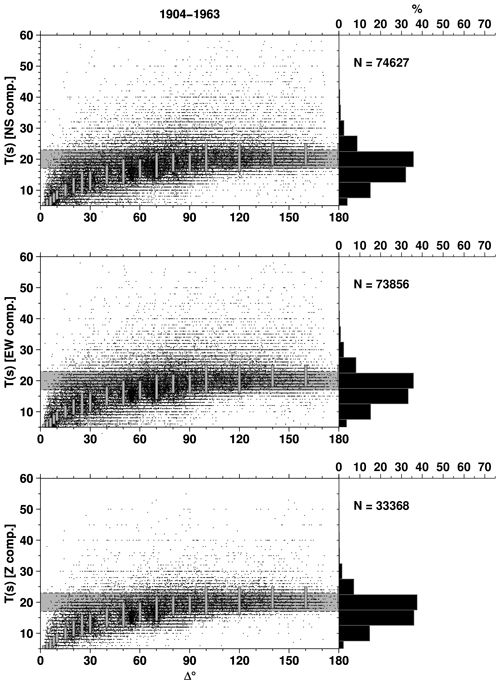
Figure 7Three-component distance-period plots of for surface wave readings digitized from printed bulletins for earthquakes that occurred before 1964. The horizontal grey shaded area depicts measurements around 20 s, whereas the vertical grey bars represent the expected period ranges at various distances (Vanĕk et al., 1962) as published in Table 3.2.2.1 of Willmore (1979). The histograms on the right-hand side show the period distribution in bins of 5 s. See text for details.
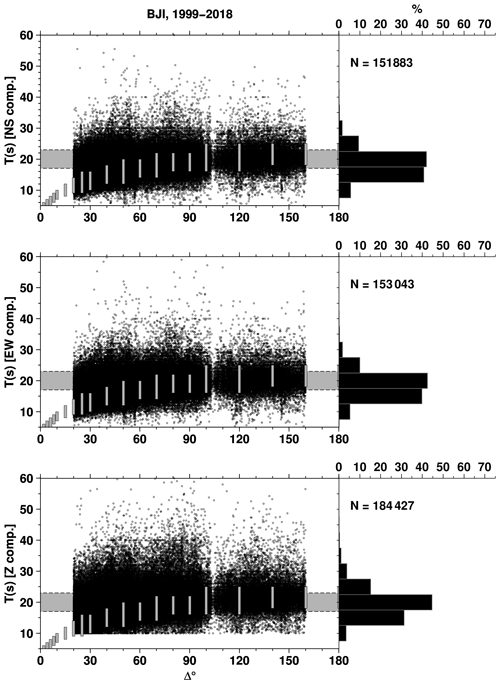
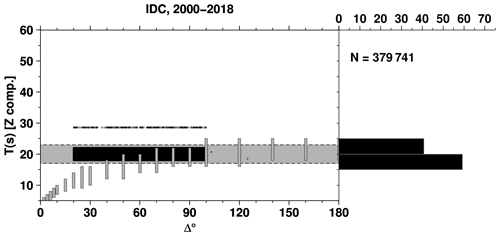
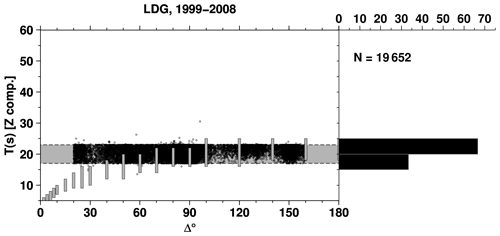
However, not all reporters fully adopted WWSSN standards. Indeed, among the largest ones (Fig. 3), agency BJI, MOS and PRU report surface wave amplitudes in broad period ranges. The delta-period plots of those agencies are shown in Appendix A (Figs. A2, A3 and A4). Other agencies, instead, strictly adhere to amplitude-period measurements around 20 s (Figs. A5, A6 and A7, for agencies IDC, LDG and NEIC from 2009, respectively).
As a final remark in this section, we reiterate, as already done in Di Giacomo et al. (2015a), that the differences in distance and period ranges do not introduce a discontinuity in the Ms estimates before and after 1964. The expansion of the delta-period limits pre-1964 is allowed by the data, and it often gives us the opportunity to increase Nsta for our network Ms computation in a time period where surface wave data were scant (compared to current times) and not digitally available (hence the need of not discarding precious and hard-to-get data). As a result of our approach, about 40 % of the pre-1964 earthquakes we list in the ISC Ms dataset gained from 1 to 28 station magnitudes, and 1000 of those earthquakes would not have network Ms without delta-period augmentation. This is synthesized in Fig. 9. An area encompassing the North Atlantic mid-oceanic ridges, the Euro-Mediterranean and the Middle East benefitted the most thanks to European and central Asian stations that measured surface waves in broad period ranges at distances below 20∘.
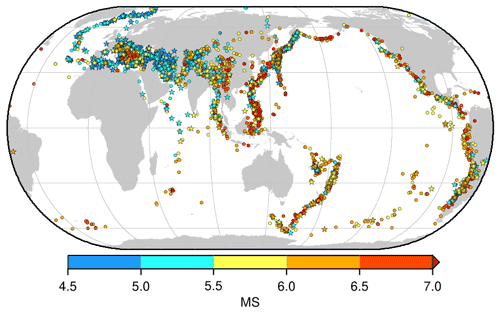
Figure 9Map of the pre-1964 earthquakes where the expansion of the delta-period ranges compared to the current ISC practice allowed us to better constrain Ms. Stars are for the 1000 earthquakes that otherwise would not have network Ms. All symbols colour-coded by Ms. Map drawn using the Generic Mapping Tools (GMT) (Wessel et al., 2013) software.
The ISC Ms dataset has a minimum cut-off magnitude of 4.5. Earthquakes with lower Ms values are available in the ISC Bulletin but mostly in recent decades. The major improvements regard earthquakes prior to 1964, where, according to our records, out of 10 057 earthquakes the ISC is the first to compute Ms for 4940 of them (their distribution and timeline is shown in Fig. A8). Considering the whole ISC Ms dataset, major features can be discussed using Fig. 10, where we show the magnitude timeline, number of earthquakes per year for various magnitude thresholds and annual magnitude of completeness (Mc) computed with the maximum curvature method of Wiemer and Wyss (2000). The completeness analysis is only meant to highlight general features of the dataset (a more detailed study in this respect, as the one by Michael, 2014, is not the aim of this work). As in any other earthquake catalogue, we cannot include all shallow earthquakes since some of them may be poorly recorded or not matching our selection criteria. Hence, we perform annual Mc estimations knowing that the dataset may have missing records. This is more likely to be the case in the first part of the last century. As a result, annual Mc uncertainties (error bars in the top panel of Fig. 10) are generally larger for the early decades of the last century compared to recent times.
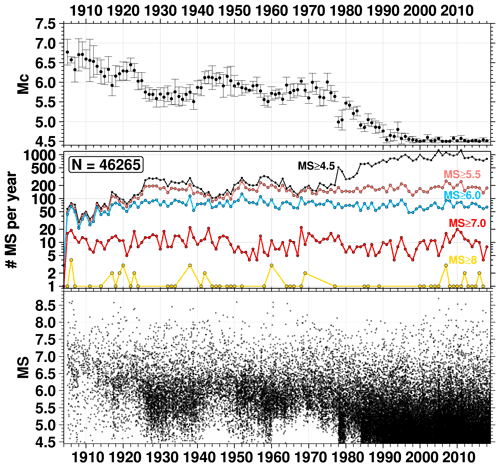
Figure 10Bottom panel: magnitude timeline of the ISC Ms dataset. Middle panel: number of Ms per year for different Ms thresholds (4.5, 5.5, 6.0, 7.0 and 8.0 in black, light red, blue, red and yellow, respectively). Top panel: annual magnitude of completeness Mc (Wiemer and Wyss, 2000) in the dataset, shown as average ±1 standard deviation.
Overall, we include Ms<5.5 earthquakes mostly from the 1980s, and Mc approaches approximately 4.5 in the last 20 years. We note that we were able to obtain more solutions at the low magnitude end particularly in the late-1920s–1930s. This has been possible thanks to the establishment of the backbone network in former Soviet Union territory and a general increase of Ms stations in other areas (see annual station maps in International Seismological Centre, 2021d). An overall dip is observed in the 1940s, most likely caused by the disruption of World War II on the seismic network (Di Giacomo et al., 2018). The period 1960–1977 also features fewer earthquakes below 5.5 than the previous and following decades. This is due both to the limited number of stations available and the fact that we digitized surface wave data from the 1960s printed station bulletins only for earthquakes selected in the first version of the ISC-GEM Catalogue (magnitude 5.5 and above, Storchak et al., 2013). In Sect. 6 we propose activities that are likely to mitigate significantly the deficiencies of the ISC Ms dataset in most of the 1960s–1970s. Another fluctuation at low magnitudes is observed in the early-1980s. Indeed both the annual counts and Mc show a significant variation from 1978–1979 (Mc close to 5.0) to 1980–1983 (higher Mc ranging between 5.2–5.5). We believe this is due to the temporary absence of MOS surface wave data in 1980–1983 (see Sect. 6), which was included into the rebuilt ISC Bulletin (Storchak et al., 2020) from 1984 onward (Mc dropping again to about 5 and below).
Weaker variations are seen for moderate size earthquakes (i.e., Ms between 5.0 and 6.0). The early part of last century (up to the mid-1920s) is clearly complete above magnitude 6.0, whereas since the 1950s the frequency of Ms 5.5 and 6.0 appears rather stable. Pronounced variations are observed from the mid-1920s to the 1940s for reasons mentioned above.
Variations over time of the frequency of large (i.e., Ms≥6.0) earthquakes based on past catalogues have been the subject of debate in past literature. In particular, Pérez and Scholz (1984) suggested that, under the assumption of constant rate earthquake occurrence, temporal variations of large shallow earthquakes were driven by instrumental changes. Ogata and Abe (1991) and more recently Ogata (2021), however, suggest that variations in the frequency of global large earthquakes are a real effect of the Earth's seismic activity (long-range dependence nature of earthquake occurrence). Therefore, to further discuss the rate of the Earth's large shallow seismicity, we show in Fig. 11 the cumulative number of strong to major earthquakes in the ISC Ms dataset similarly to the figures in Pérez and Scholz (1984) and Pérez (1999). Compared to these works, our rates for Ms ≥ 7.0 and 6.0 in different time intervals (Table 2) show some significant differences and lack large jumps from one period to another. This is strikingly evident for the Ms ≥ 6.0 distribution, where the Pérez (1999) rate goes down to 38 yr−1 during 1964–1978 compared to a rate of about 78 yr−1 in the ISC Ms dataset. We note that this period in the original ISC Bulletin lacked the ISC's own computations of Ms. Therefore, Pérez (1999) rates may have been biased by using largely incomplete inputs.
(Pérez and Scholz, 1984)(Pérez, 1999)Table 2Rates of seismicity in the ISC Ms dataset and in Pérez and Scholz (1984); Pérez (1999). See text for details.
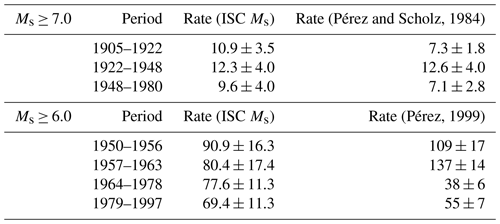
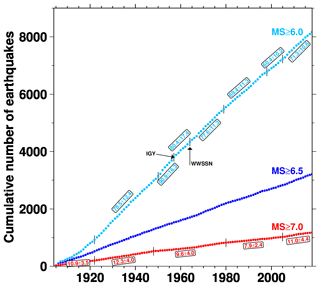
Figure 11Cumulative number of earthquakes with Ms ≥ 7.0 (red), ≥ 6.5 (blue) and ≥6.0 (cyan). The vertical black segments on the red and cyan symbols locate the time periods considered by Pérez and Scholz (1984) for Ms ≥ 7.0 (up to 1980) and Pérez (1999) Ms ≥ 6.0 (from 1950 to 1997), respectively. IGY stands for International Geophysical Year started in 1957. See text for details.
In general, we see that shallow seismicity rates are characterized by a global low occurring between the great earthquakes of the early 1960s and the beginning of the current century (Ammon et al., 2010). Although rates for Ms ≥ 7.0 in the first part of the last century are comparable to the rate we have observed since 2005, it seems that rates for Ms ≥ 6.0 from the WWSSN introduction appear to be lower than rates in the first part of the last century. We also assessed if by declustering (Reasenberg, 1985) the Ms catalogue the rates would be different but only small variations occur, and, more importantly, relative differences between time periods remain. This is not surprising as the ISC Ms dataset does not contain a large number of aftershocks for Ms ≥ 6.0 (by the very nature of Ms it is more difficult to obtain it for aftershocks of large earthquakes due to association challenges in overlapping signals, particularly in routine operations).
It is not the aim of this work to investigate whether fluctuations in seismic activity rates are partially due to instrumental changes or purely due to natural variations of the Earth's seismicity. However, we believe that the ISC Ms dataset is one of the best inputs to date to do such studies. In this context it is important to point out that the quality of instrumental earthquake catalogues depends on the quality of the data available at the time of processing. In our experience, for long-term datasets it is almost unavoidable that different types of shortcomings may occur in different time periods, for example due to external factors (e.g., network deficiencies during world wars) and that faulty individual entries may be present. It is of paramount importance, therefore, that datasets are well documented and that users know how they are created in order to properly use them for research.
By the time Ms was introduced by Gutenberg (1945), no magnitude 9 or 9+ earthquake had been recorded instrumentally. The occurrence of the 4 November 1952 Kamchatka earthquake and the well-know great earthquakes of the early 1960s (22 May 1960 Chile and 28 March 1964 Alaska earthquakes) drew attention to a shortcoming of Ms, which is commonly referred to as magnitude saturation. This was one of the factors that led Kanamori (1977) and Hanks and Kanamori (1979) to introduce the moment magnitude Mw, which is based on a physical parameter of the seismic source (i.e., seismic moment) rather than amplitude-period measurements.
In Fig. 12 we compare the ISC Ms dataset with Mw from GCMT and the bibliographic search for pre-1976 earthquakes of Lee and Engdahl (2015) and follow-up updates as listed at http://www.isc.ac.uk/iscgem/mw_bibliography.php (last access: August 2021; hereafter referred to as Mw from the literature). Such magnitude comparison has been discussed in several papers, particularly to derive magnitude conversion relationships. For this work, however, we show this comparison to focus on the Ms saturation issue and briefly touch upon earthquakes with large (Mw–Ms) differences.

Figure 12Comparison of Ms with Mw from GCMT (black dots) and from the literature (red, Lee and Engdahl, 2015, and further updates listed at http://www.isc.ac.uk/iscgem/mw_bibliography.php, last access: August 2021). The black solid curve is a digitized version of the midpoint Mw–Ms curve shown in Fig. 4b of Kanamori (1983). The largest 10 earthquakes in terms of Mw (bulls eye symbols) are also identified by the event code in the ISC Event Bibliography (http://www.isc.ac.uk/event_bibliography/index.php, last access: August 2021).
The 10 largest earthquakes (in Mw terms) ever recorded are easily identified in Fig. 12 by the event code in the ISC Event Bibliography (Di Giacomo et al., 2014; International Seismological Centre, 2021a). As already summarized by Kanamori (1983), the saturation of Ms is generally expected to start between 8.2 and 8.5. For recent (26 December 2004, Sumatra, and 11 March 2011, Tohoku) and pre-GCMT earthquakes (the above-mentioned 1960 Chile and 1964 Alaska earthquakes) with Mw 9 and above, the effects of saturation are quite severe and vary between 0.6 and 1 magnitude unit (m.u.). However, for earthquakes with Mw between 8 and 9, the variation of the saturation appears to vary much more (from near to 0 up to 1 m.u.). For example, the 27 February 2010 Mw 8.8 Maule earthquake has an Ms only 0.25 m.u. smaller, which is close to common Mw–Ms differences observed across a wide magnitude range before the saturation of Ms is expected. Figure 12 shows other examples where Mw and Ms are close to the 1:1 line between 8 and 8.7 (including the 15 August 1950 Assam earthquake). With regard to great earthquakes with large Mw–Ms differences, some of those belong to a peculiar category, the so-called tsunami earthquakes (Kanamori, 1972). These have a relatively small Ms compared to their Mw and are well documented in the literature. The most striking example is probably the 1 April 1946 Aleutian earthquake, where our Ms of 7.4 is much smaller than the Mw 8.6 by López and Okal (2006). On the other hand, large differences are observed for other earthquakes (e.g., 4 February 1965 Rat Islands and 28 March 2005 Nias earthquakes) not strictly considered tsunami earthquakes.
In light of the Ms values for the largest earthquakes ever recorded, we support the remarks by Bormann (2011) that it would be more correct to speak of Ms underestimation rather than saturation, as the latter would need to be systematically observable for great earthquakes with Mw between 8.2–8.5 and above. However, we have shown that underestimation (“saturation”) depends on the type of earthquake, and it is severe only for a handful of the largest earthquakes ever recorded (Mw ≥ 9). Therefore, the underestimation (saturation) of Ms should not discourage researches to use it as a reliable measure of the size of shallow earthquakes. We also suggest that Ms and Mw, as expressions at different periods of the earthquake size, should be used together to better characterize the source properties of an earthquake.
Overall, the magnitude comparison of Fig. 12 shows that Ms is typically close to Mw over the magnitude range 6.2 to 8, whereas for smaller earthquakes Ms is usually smaller than Mw. However, some earthquakes show large differences (examples listed in Table A1 for Ms ≫ Mw and vice versa). For the sake of brevity we do not discuss every earthquake with such large differences but touch only on the case of the 18 April 1906 San Francisco earthquake (SANFRANCISCO1906, first event in Table A1) to clarify our reasons for keeping such entries in the ISC Ms dataset.
The Ms of the SANFRANCISCO1906 earthquake is dominated by stations located in Germany (GTT, POT, LEI and JEN), plus Apia (API, Samoa Islands) and Osaka (OSA, Japan) at different azimuths. All station Ms values are consistently above 8, resulting in a network Ms of 8.6 ± 0.1 (full station details listed under event 16957905 in International Seismological Centre, 2021d). This is a much higher value than the Mw=7.7 obtained by Wald et al. (1993). Such outliers occur in most earthquake catalogues for various reasons. As mentioned earlier, parameters of individual earthquakes are the result of the processing of the data available at a given time. For the SANFRANCISCO1906 earthquake, instrumental issues could have played a major role in the high Ms value. However, we believe that listing such results in the dataset (rather than deprecating) is important for legacy reasons and that users may still use such information for further studies and, ideally, motivate the community to attempt additional data collection. The latter is an activity that we will continue and discuss in the next section.
The maintenance and development of the ISC Ms dataset will not cease with this work. First, we intend to routinely add the last calendar year reviewed by the ISC. This means that once the ISC review is over for 2019 earthquakes, the ISC Ms dataset will be updated and end in 2019 and so on in following years. Secondly, we aim at refining and adding Ms solutions for past years. Indeed, we are aware that the Ms station contribution can be improved in certain years. One example was already pointed out for 1980–1983, where MOS surface wave data were not included in time for the ISC rebuild project (Storchak et al., 2020). By adding such data we expect to fill (or, at least, partially fill) the gap shown in those years for low Ms earthquakes, as shown in Fig. 10.
Before the early 1980s, the following time periods may benefit from additional station contributions.
-
During the 1970s, one source that, to our knowledge, has never been digitized is the printed bulletins of the Chinese network. Tens of stations with plenty of surface wave data are available in those bulletins, which can potentially increase Nsta for earthquakes already listed in the dataset and allow us to compute Ms for several new ones.
-
Due to time and funding limitations, the digitization of 1964–1970 surface wave data from printed station/network bulletins (Di Giacomo et al., 2015b) was not done for all bulletins available at the ISC, and, if done, it focused on earthquakes with magnitude 5.5 and above. Hence, a more comprehensive approach for surface wave data digitization is desirable for these years.
-
For the period 1936–1963 we are finalizing the digitization of station arrival times for earthquakes in the bulletins of the Bureau Central International de Séismologie (BCIS, 1933–1968) that were not listed in the International Seismological Summary (ISS, 1918–1963) (earthquakes in this time period that are not listed in the ISS currently have no station data digitally available in the ISC database). Once this undertaking is finished, we will add surface wave data for earthquakes recorded teleseismically and attempt to obtain Ms for as many earthquakes as possible.
-
Improvements in the first part of the last century are more challenging as we have nearly exhausted the digitization of printed bulletins available to us. It is hard to verify if our surface wave data collection from printed bulletins is as complete as possible. Assistance in this respect from observatories and archives around the world would be highly appreciated (the presence or absence of a set of station data can be easily checked in the ISC Ms dataset).
Hence, if conditions permit, we wish to continue the digitization of printed bulletins and add surface wave data in order to improve the Ms solutions for a significant fraction of pre-1980 earthquakes. However, we stress that additional contributions for earthquakes in recent decades are welcome as well, and we will strive to include them in the ISC Bulletin and, in turn, in the ISC Ms dataset.
The ISC Ms dataset (International Seismological Centre, 2021d) is available in the ISC Dataset Repository at https://doi.org/10.31905/0N4HOS2D. The dataset is released without licence. It is composed of a catalogue file (CSV format) and annual files containing the underlying station data used to obtain Ms for each earthquake. All parameters in the catalogue and annual files are detailed in the README file in International Seismological Centre (2021d). The annual files include, below the earthquake parameters, two data blocks: first the station magnitude block (sorted by distance) and then the phase data block, which includes the original amplitude and period measurements as well as the intermediate magnitude results (amplitude and reading magnitude, MsZ and MsH) that lead to the station magnitude computation (see Sect. 2). Annual station plots and annual station lists are also included as well as the file with the data points to generate Fig. 12.
An aspect that differentiates Ms from other magnitude scales is that it can be computed from original measurements of surface wave amplitudes and periods throughout the instrumental period. The ISC Ms dataset we presented here includes 100+ years of earthquakes with Ms ≥ 4.5 starting from the dawn of modern instrumental seismology (1904) up to the last complete reviewed year by the ISC (2018). This achievement is possible as a result of a monumental undertaking thanks to which pre-1971 measurements of surface waves were digitized from a multitude of printed station/network bulletins.
We have summarized the evolution of the station network contributing to Ms and highlighted its shortcomings (e.g., significant lack of stations in the Southern Hemisphere for a large part of the last century) and strengths (e.g., high density in Europe that allowed us to obtain Ms for earthquakes in a wide area in low magnitude ranges before the introduction of modern digital stations). The expansion of the delta-period ranges, as allowed by the data, resulted in more and better constrained Ms estimations for about 40 % of the pre-1964 earthquakes.
We have discussed the Ms underestimation for the largest earthquakes ever recorded and pointed out the presence of occasional large differences with Mw. Those entries are listed for legacy and other purposes and may require further work.
Inevitably, the dataset has fluctuations in terms of completeness and earthquake rates over different time periods. We discussed the most relevant ones and outlined plans for continuing and improving this dataset.
In the years to come we envisage the ISC Ms dataset as one of the best inputs researchers can use for various seismological studies, including the Earth's seismicity patterns.
Here we show figures in support of the main text. Most of them regard additional delta-period plots similar to Fig. 7 for major Ms reporters.
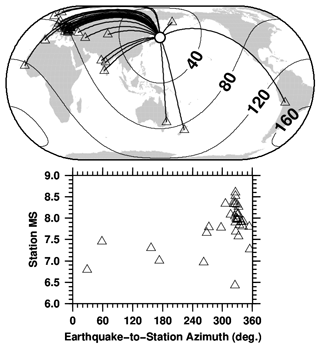
Figure A1Top: map showing the location of the 20 March 1960 earthquake off the east coast of Honshu (event ID: 878564, white circle) and the stations (triangles) contributing to the network Ms=7.9. Contours every 40∘ distance shown for guidance. Map drawn using the Generic Mapping Tools (GMT) (Wessel et al., 2013) software; Bottom: azimuthal distribution of the single station Ms for this event.
Table A1Examples of Mw<8.2 earthquakes characterized by large differences between Mw and Ms. Mw is from the literature for pre-1976 earthquakes and GCMT otherwise. The last column is the ISC event identifier.

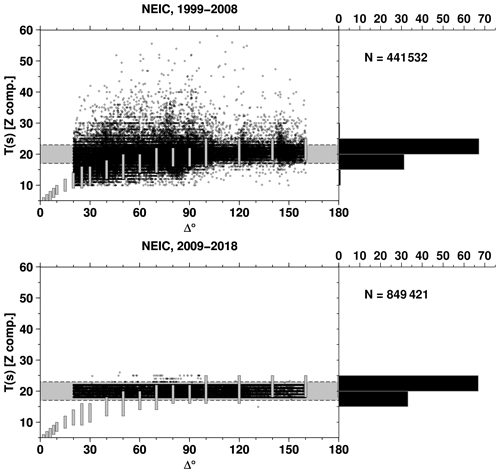
Figure A7As for Fig. 7 but for reporter NEIC (vertical component only). Here we split the plot in two time periods to emphasize the change in 2009 by NEIC in reporting surface wave amplitudes strictly around 20 s.

Figure A8Map colour-coded by Ms and timeline of the pre-1964 earthquakes where, according to our records, Ms has been computed for the first time. Map drawn using the Generic Mapping Tools (GMT) (Wessel et al., 2013) software.
DDG is the lead author, prepared the dataset and figures, supervised the digitization of the surface wave data, and vetted the Ms results up to 1963. DAS obtained the funding for the work and established and maintained operational connections with many data providers, especially for obtaining additional datasets previously unavailable. Both authors contributed to the manuscript and approved the final version.
The contact author has declared that neither they nor their co-author has any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We are grateful to all reporters that contribute or have contributed data to the ISC, particularly in terms of Ms for this work. We thank Kenji Satake, Emmanuel Scordilis, Nobuo Hamada and an anonymous reviewer for their comments and suggestions that helped us to improve the manuscript. Special thanks go to many colleagues that lent or donated to the ISC station/network printed bulletins originally not available to us, as summarized at http://www.isc.ac.uk/printedStnBulletins/ (last access: November 2021). Daniela Olaru and former data entry staff were instrumental to this work for digitizing the surface wave data from printed bulletins. The ISC is able to continue its mission thanks to the support of its members (http://www.isc.ac.uk/members/, last access: November 2021) and sponsors (http://www.isc.ac.uk/sponsors/, last access: November 2021). All figures were drawn using the Generic Mapping Tools (Wessel et al., 2013).
This work was partially funded by NSF grants 1811737, 1417970 and 0949072 as well as USGS awards G14AC00149, G15AC00202, G18AP00035 and G19AS00033.
This paper was edited by Kirsten Elger and reviewed by Kenji Satake, Emmanuel Scordilis, and one anonymous referee.
Abe, K.: Magnitudes of large shallow earthquakes from 1904 to 1980, Phys. Earth Planet. In., 27, 72–92, https://doi.org/10.1016/0031-9201(81)90088-1, 1981. a
Abe, K.: Complements to “Magnitudes of large shallow earthquakes from 1904 to 1980”, Phys. Earth Planet. In., 34, 17–23, https://doi.org/10.1016/0031-9201(84)90081-5, 1984. a
Abe, K. and Noguchi, S.: Determination of magnitude for large shallow earthquakes 1898–1917, Phys. Earth Planet. In., 32, 45–59, https://doi.org/10.1016/0031-9201(83)90077-8, 1983a. a
Abe, K. and Noguchi, S.: Revision of magnitudes of large shallow earthquakes, 1897–1912, Phys. Earth Planet. In., 33, 1–11, https://doi.org/10.1016/0031-9201(83)90002-x, 1983b. a
Adams, R. D., Hughes, A. A., and McGregor, D. M.: Analysis procedures at the International Seismological Centre, Phys. Earth Planet. In., 30, 85–93, https://doi.org/10.1016/0031-9201(82)90093-0, 1982. a
Allen, T. I., Marano, K. D., Earle, P. S., and Wald, D. J.: PAGER-CAT: A Composite Earthquake Catalog for Calibrating Global Fatality Models, Seismol. Res. Lett., 80, 57–62, https://doi.org/10.1785/gssrl.80.1.57, 2009. a
Ammon, C. J., Lay, T., and Simpson, D. W.: Great Earthquakes and Global Seismic Networks, Seismol. Res. Lett., 81, 965–971, https://doi.org/10.1785/gssrl.81.6.965, 2010. a
BCIS: Bureau Central International de Séismologie, monthly issues, 1933–1968. a
Bondár, I. and Storchak, D. A.: Improved location procedures at the International Seismological Centre, Geophys. J. Int., 186, 1220–1244, https://doi.org/10.1111/j.1365-246x.2011.05107.x, 2011. a
Bondár, I., Myers, S. C., Engdahl, E. R., and Bergman, E. A.: Epicentre accuracy based on seismic network criteria, Geophys. J. Int., 156, 483–496, https://doi.org/10.1111/j.1365-246x.2004.02070.x, 2004. a
Bondár, I., Engdahl, E. R., Villaseñor, A., Harris, J., and Storchak, D.: ISC-GEM: Global Instrumental Earthquake Catalogue (1900–2009), II. Location and seismicity patterns, Phys. Earth Planet. In., 239, 2–13, https://doi.org/10.1016/j.pepi.2014.06.002, 2015. a
Bormann, P.: Earthquake, Magnitude, in: Encyclopedia of Solid Earth Geophysics, edited by: Gupta, H. K., Springer, Dordrecht, 207–218, https://doi.org/10.1007/978-90-481-8702-7_3, 2011. a
Bormann, P. (Ed.): Magnitude calibration formulas and tables, comments on their use and complementary data, in: New Manual of Seismological Observatory Practice 2 (NMSOP-2), Potsdam, Deutsches GeoForschungsZentrum GFZ, 1–19, https://doi.org/10.2312/GFZ.NMSOP-2_DS_3.1, 2012. a
Bormann, P., Liu, R., Xu, Z., Ren, K., Zhang, L., and Wendt, S.: First Application of the New IASPEI Teleseismic Magnitude Standards to Data of the China National Seismographic Network, B. Seismol. Soc. Am., 99, 1868–1891, https://doi.org/10.1785/0120080010, 2009. a
Bormann, P., Wendt, S., and Di Giacomo, D.: Seismic Sources and Source Parameters, in: New Manual of Seismological Observatory Practice 2 (NMSOP-2), edited by: Bormann, P., Potsdam, Deutsches GeoForschungsZentrum GFZ, 1–259, https://doi.org/10.2312/GFZ.NMSOP-2_CH3, 2012. a, b, c
Coenraads, R. R.: The San Calixto Observatory in La Paz, Bolivia. Eighty years of operation, Director Dr. Lawrence A. Drake S.J., Journal and Proceedings – Royal Society of New South Wales, 126, 191–198, 1993. a
Di Giacomo, D. and Storchak, D. A.: A scheme to set preferred magnitudes in the ISC Bulletin, J. Seismol., 20, 555–567, https://doi.org/10.1007/s10950-015-9543-7, 2016. a
Di Giacomo, D., Storchak, D. A., Safronova, N., Ozgo, P., Harris, J., Verney, R., and Bondár, I.: A New ISC Service: The Bibliography of Seismic Events, Seismol. Res. Lett., 85, 354–360, https://doi.org/10.1785/0220130143, 2014. a
Di Giacomo, D., Bondár, I., Storchak, D. A., Engdahl, E. R., Bormann, P., and Harris, J.: ISC-GEM: Global Instrumental Earthquake Catalogue (1900–2009), III. Re-computed MS and mb, proxy MW, final magnitude composition and completeness assessment, Phys. Earth Planet. In., 239, 33–47, https://doi.org/10.1016/j.pepi.2014.06.005, 2015a. a, b, c
Di Giacomo, D., Harris, J., Villaseñor, A., Storchak, D. A., Engdahl, E. R., and Lee, W. H. K.: ISC-GEM: Global Instrumental Earthquake Catalogue (1900–2009), I. Data collection from early instrumental seismological bulletins, Phys. Earth Planet In., 239, 14–24, https://doi.org/10.1016/j.pepi.2014.06.003, 2015b. a, b, c, d
Di Giacomo, D., Engdahl, E. R., and Storchak, D. A.: The ISC-GEM Earthquake Catalogue (1904–2014): status after the Extension Project, Earth Syst. Sci. Data, 10, 1877–1899, https://doi.org/10.5194/essd-10-1877-2018, 2018. a, b, c, d
Drake, L. A.: Riverview Observatory, in: St. Ignatius' Centennial 1880–1980, edited by: Fracer, C. and Scarlett, E. L., St. Ignatius College, Lane-Cove NSW, 1993. a
Dziewonski, A. M., Chou, T.-A., and Woodhouse, J. H.: Determination of earthquake source parameters from waveform data for studies of global and regional seismicity, J. Geophys. Res.-Sol Ea., 86, 2825–2852, https://doi.org/10.1029/jb086ib04p02825, 1981. a
Ekström, G., Nettles, M., and Dziewoński, A. M.: The global CMT project 2004–2010: Centroid-moment tensors for 13,017 earthquakes, Phys. Earth Planet. In., 200–201, 1–9, https://doi.org/10.1016/j.pepi.2012.04.002, 2012. a
Engdahl, E. R. and Villaseñor, A.: Global seismicity: 1900–1999, in: International Handbook of Earthquake and Engineering Seismology, edited by: Lee, W. H. K., Kanamori, H., Jennings, J. C., and Kisslinger, C., vol. A, chap. 41, Academic Press, San Diego, 665–690, 2002. a
Gutenberg, B.: Amplitudes of surface waves and magnitudes of shallow earthquakes, Bulletin of the Seismological Society of America, 35, 3–12, 1945. a, b
Gutenberg, B. and Richter, C.: Seismicity of the Earth and Associated Phenomena, Princeton Univ. Press, Princeton, NJ, 310 pp., 1954. a
Hanks, T. C. and Kanamori, H.: A moment magnitude scale, J. Geophys. Res., 84, 2348–2350, https://doi.org/10.1029/jb084ib05p02348, 1979. a, b
Herak, M. and Herak, D.: Distance dependence of Ms and calibrating function for 20 second Rayleigh waves, B. Seismol. Soc. Am., 83, 1881–1892, 1993. a
IASPEI: Summary of Magnitude Working Group recommendations on standard procedures for determining earthquake magnitudes from digital data, available at: ftp://ftp.iaspei.org/pub/commissions/CSOI/Summary_WG_recommendations_20130327.pdf (last access: November 2021), 2013. a, b, c, d
International Seismological Centre: On-line Event Bibliography, https://doi.org/10.31905/EJ3B5LV6 [data set], 2021a. a
International Seismological Centre: International Seismograph Station Registry (IR), https://doi.org/10.31905/EL3FQQ40 [data set], 2021b. a
International Seismological Centre: On-line Bulletin, https://doi.org/10.31905/D808B830 [data set], 2021c. a
International Seismological Centre: The ISC MS dataset for shallow earthquakes since 1904, ISC Seismological Dataset Repository, https://doi.org/10.31905/0N4HOS2D [data set], 2021d. a, b, c, d, e, f, g, h
ISS: International Seismological Summary, annual volumes, 1918–1963. a
Kanamori, H.: Mechanism of tsunami earthquakes, Phys. Earth Planet. In., 6, 346–359, https://doi.org/10.1016/0031-9201(72)90058-1, 1972. a
Kanamori, H.: The energy release in great earthquakes, J. Geophys. Res., 82, 2981–2987, https://doi.org/10.1029/jb082i020p02981, 1977. a, b
Kanamori, H.: Magnitude scale and quantification of earthquakes, Tectonophysics, 93, 185–199, https://doi.org/10.1016/0040-1951(83)90273-1, 1983. a, b
Kárník, V., Kondorskaya, N. V., Riznitchenko, J. V., Savarensky, E. F., Soloviev, S. L., Shebalin, N. V., Vanek, J., and Zátopek, A.: Standardization of the earthquake magnitude scale, Stud. Geophys. Geod., 6, 41–48, https://doi.org/10.1007/BF02590040, 1962. a
Lee, W. H. K. and Engdahl, E. R.: Bibliographical search for reliable seismic moments of large earthquakes during 1900–1979 to compute MW in the ISC-GEM Global Instrumental Reference Earthquake Catalogue, Phys. Earth Planet. In., 239, 25–32, https://doi.org/10.1016/j.pepi.2014.06.004, 2015. a, b
López, A. M. and Okal, E. A.: A seismological reassessment of the source of the 1946 Aleutian “tsunami” earthquake, Geophys. J. Int., 165, 835–849, https://doi.org/10.1111/j.1365-246x.2006.02899.x, 2006. a
Michael, A. J.: How Complete is the ISC-GEM Global Earthquake Catalog?, B. Seismol. Soc. Am., 104, 1829–1837, https://doi.org/10.1785/0120130227, 2014. a
Ogata, Y.: Visualizing heterogeneities of earthquake hypocenter catalogs: modeling, analysis, and compensation, Progr. Earth Pl. Sci., 8, https://doi.org/10.1186/s40645-020-00401-8, 2021. a
Ogata, Y. and Abe, K.: Some Statistical Features of the Long-Term Variation of the Global and Regional Seismic Activity, Int. Stat. Rev., 59, 139–161, https://doi.org/10.2307/1403440, 1991. a, b
Oliver, J. and Murphy, L.: WWNSS: Seismology's Global Network of Observing Stations, Science, 174, 254–261, https://doi.org/10.1126/science.174.4006.254, 1971. a
Pacheco, J. F. and Sykes, L. R.: Seismic moment catalog of large shallow earthquakes, 1900 to 1989, B. Seismol. Soc. Am., 82, 1306–1349, 1992. a
Peterson, J. R. and Hutt, C. R.: World-Wide Standardized Seismograph Network: a data users guide, U.S. Geological Survey Open-File Report 2014–1218, 74 pp., https://doi.org/10.3133/ofr20141218, 2014. a
Pérez, O. J.: Revised world seismicity catalog (1950–1997) for strong (Ms ≧ 6) shallow (h ≦ 70 km) earthquakes, B. Seismol. Soc. Am., 89, 335–341, 1999. a, b, c, d, e, f, g
Pérez, O. J. and Scholz, C. H.: Heterogeneities of the instrumental seismicity catalog (1904–1980) for strong shallow earthquakes, B. Seismol. Soc. Am., 74, 669–686, 1984. a, b, c, d, e, f
Reasenberg, P.: Second-order moment of central California seismicity, 1969–1982, J. Geophys. Res.-Sol. Ea., 90, 5479–5495, https://doi.org/10.1029/jb090ib07p05479, 1985. a
Rezapour, M. and Pearce, R. G.: Bias in surface-wave magnitude Ms due to inadequate distance corrections, B. Seismol. Soc. Am., 88, 43–61, 1998. a
Richter, C. F.: An instrumental earthquake magnitude scale, B. Seismol. Soc. Am., 25, 1–32, 1935. a
Schering, H.: Seismische Registrierungen in Göttingen im Jahre 1904, Nachrichten von der Königlichen Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-physikalische Klasse, 181–200, 1905. a
Storchak, D. A., Di Giacomo, D., Bondár, I., Engdahl, E. R., Harris, J., Lee, W. H. K., Villaseñor, A., and Bormann, P.: Public Release of the ISC–GEM Global Instrumental Earthquake Catalogue (1900–2009), Seismol. Res. Lett., 84, 810–815, https://doi.org/10.1785/0220130034, 2013. a
Storchak, D. A., Harris, J., Brown, L., Lieser, K., Shumba, B., Verney, R., Di Giacomo, D., and Korger, E. I. M.: Rebuild of the Bulletin of the International Seismological Centre (ISC), part 1: 1964–1979, Geosci. Lett., 4, 32, https://doi.org/10.1186/s40562-017-0098-z, 2017. a, b, c
Storchak, D. A., Harris, J., Brown, L., Lieser, K., Shumba, B., and Di Giacomo, D.: Rebuild of the Bulletin of the International Seismological Centre (ISC) – part 2: 1980–2010, Geosci. Lett., 7, 18, https://doi.org/10.1186/s40562-020-00164-6, 2020. a, b, c, d, e
Udias, A. and Stauder, W.: The Jesuit Contribution to Seismology, Seismol. Res. Lett., 67, 10–19, https://doi.org/10.1785/gssrl.67.3.10, 1996. a
Vanĕk, J., Zapotek, A., Karnik, V., Kondorskaya, N. V., Riznichenko, Y. V., Savarensky, E. F., Solov’yov, S. L., , and Shebalin, N. V.: Standarizaciya shkaly magnitude, Izvestiya Akad. SSSR., Ser. Geofiz., 2, 153–158 (with English translation in 1962 by D. G. Frey, published in Izv. Geophys, Ser.), 1962 (in Russian). a, b, c
von Seggern, D.: The effects of radiation patterns on magnitude estimates, B. Seismol. Soc. Am., 60, 503–516, 1970. a
Wald, D. J., Kanamori, H., Helmberger, D. V., and Heaton, T. H.: Source study of the 1906 San Francisco earthquake, B. Seismol. Soc. Am., 83, 981–1019, 1993. a
Wessel, P., Smith, W. H. F., Scharroo, R., Luis, J., and Wobbe, F.: Generic Mapping Tools: Improved Version Released, Eos T. Am. Geophys. Un., 94, 409–410, https://doi.org/10.1002/2013eo450001, 2013. a, b, c, d, e, f
Wiemer, S. and Wyss, M.: Minimum Magnitude of Completeness in Earthquake Catalogs: Examples from Alaska, the Western United States, and Japan, B. Seismol. Soc. Am., 90, 859–869, https://doi.org/10.1785/0119990114, 2000. a, b
Willmore, P.: Manual of Seismological Observatory Practice, World Data Center A for Solid Earth Geophysics, Report SE-20, 165 pp., 1979. a
- Abstract
- Introduction
- Reporters and Ms recomputation
- Station data
- Catalogue properties
- On the Ms saturation and large differences with Mw
- Future developments
- Data availability
- Conclusions
- Appendix A: Additional plots
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References
- Abstract
- Introduction
- Reporters and Ms recomputation
- Station data
- Catalogue properties
- On the Ms saturation and large differences with Mw
- Future developments
- Data availability
- Conclusions
- Appendix A: Additional plots
- Author contributions
- Competing interests
- Disclaimer
- Acknowledgements
- Financial support
- Review statement
- References