the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Into the Noddyverse: a massive data store of 3D geological models for machine learning and inversion applications
Jiateng Guo
Yunqiang Li
Mark Lindsay
Richard Scalzo
Jérémie Giraud
Guillaume Pirot
Ed Cripps
Vitaliy Ogarko
Unlike some other well-known challenges such as facial recognition, where machine learning and inversion algorithms are widely developed, the geosciences suffer from a lack of large, labelled data sets that can be used to validate or train robust machine learning and inversion schemes. Publicly available 3D geological models are far too restricted in both number and the range of geological scenarios to serve these purposes. With reference to inverting geophysical data this problem is further exacerbated as in most cases real geophysical observations result from unknown 3D geology, and synthetic test data sets are often not particularly geological or geologically diverse. To overcome these limitations, we have used the Noddy modelling platform to generate 1 million models, which represent the first publicly accessible massive training set for 3D geology and resulting gravity and magnetic data sets (https://doi.org/10.5281/zenodo.4589883, Jessell, 2021). This model suite can be used to train machine learning systems and to provide comprehensive test suites for geophysical inversion. We describe the methodology for producing the model suite and discuss the opportunities such a model suite affords, as well as its limitations, and how we can grow and access this resource.
- Article
(2632 KB) - Full-text XML
- BibTeX
- EndNote
Although they have become the focus of intense research activity in recent times, with more papers published in the 5 years prior to 2018 than all years before that combined, machine learning (ML) techniques applied to geoscience problems date back to the middle of the last century (see Van der Baan and Jutten, 2000, and Dramsch, 2020, for reviews). ML applications relate to a whole range of geological and geophysical problems, but many of these studies face common challenges due to the nature of geoscientific data sets. Karpatne et al. (2017) summarise the principal challenges as follows:
- i.
Objects with amorphous boundaries. The form, structure and patterns of geoscience objects are much more complex than those found in the discrete spaces that ML algorithms typically deal with, consisting of changes in both the topology and the dimensionality of geoscience objects with time.
- ii.
Spatio-temporal structure. Since almost every geoscience phenomenon occurs in the realm of space and time, we need to consider the evolution of systems in order to understand the current state.
- iii.
High dimensionality. The Earth system is incredibly complex, with a huge number of potential variables, which may all impact each other, and thus many of them may have to be considered simultaneously.
- iv.
Heterogeneity in space and time. Geoscience processes are extremely variable in space and time, resulting in heterogeneous data sets in terms of both sparse and clustered data. In addition, the primary evidence for a process may be erased by subsequent processes.
- v.
Interest in rare phenomena. In a number of geoscience problems, we are interested in studying objects, processes, and events that occur infrequently in space and time, such as ore deposit formation and earthquakes.
- vi.
Multi-resolution data. Geoscience data sets are often available via different sources and at varying spatial and temporal resolutions.
- vii.
Noise, incompleteness and uncertainty in data. Many geoscience data sets are plagued with noise and missing values. In addition, we often have to deal with observational biases during data collection and interpretation.
- viii.
Small sample size. The number of samples in geoscience data sets is often limited in both space and time, which of course is accentuated by their high dimensionality (iii) and our interest in rare phenomena (v). In the case examined in this study, there are few publicly available 3D geological models, and they are stored in a wide variety of formats, rendering comparison difficult.
- ix.
Paucity of ground truth. Even though many geoscience applications involve large numbers of data, geoscience problems often lack labelled samples with ground truth.
In this study we specifically focus on six of these challenges by providing a database of 1 million 3D geological models and resulting gravity and magnetic fields. We address the spatio-temporal structure of the system by using a kinematic modelling engine that converts a sequence of deformation events into a 3D geological model. We address high dimensionality by generating a very large database of possible 3D geological models. This represents a fundamental point of difference from many ML targets such as those studying consumer preference, movie ratings or facial recognition. Although of course every human face is different, with few exceptions we share the same number of features (eyes, ears, noses), and these features' sizes and relative positions vary only within small bounds. The number, geometry, composition and relative position of features in the subsurface have very wide bounds, and this represents a major hurdle to the application of ML to characterising 3D geology. This challenge is shared by more traditional geophysical inversion approaches (Li and Oldenburg, 1998).
We address issues related to multi-resolution data by providing a “controlled” data set, at the same resolution; it offers possibilities of addressing multi-resolution issues, by subsampling or upscaling.
We address noise, incompleteness and uncertainty in data by providing synthetic data; we have noise- and uncertainty-free data, or at least under control, and complete spatial coverage over the simulation domain. The models we provide can easily have a structured or unstructured noise added to them, and they can be subsampled to reproduce incomplete data sets.
We address small sample size by generating 1 million models, which is certainly not enough to thoroughly explore the high dimensional model space; however, it illustrates the feasibility of producing large suites of models in the near future. Modern ML training sets for popular subjects such as the human face may contain tens of millions of examples (Kollias and Zafeiriou, 2019). A search of the Kaggle database of training data sets (https://kaggle.com, last access: 27 January 2022, which contains over 63 000 distinct data sets at the time of writing) had only 151 data sets with geoscience in the keywords, and only seismic catalogues featured as geophysical data. Similarly, only 59 data sets contained 3D data, and none were related to the geosciences.
Finally, we address the spatial and temporal paucity of ground truth by publishing over 1 million models for which the full 3D lithological and petrophysical distribution is provided in a labelled form for comparison with resulting gravity and magnetic fields. This challenge is also faced by geophysical inversion methods. Three-dimensional geological models built using sufficient data to reduce uncertainty arguably exist, but leaving aside a strict definition of uncertainty, well-constrained 3D geological models are primarily restricted to restricted areas of significant economic interest, specifically sedimentary basins and mineral deposits, which only represent a subset of possible geological scenarios. A number of studies have built simple or complex synthetic models as a way to overcome these problems by providing fully defined test cases for testing processing, imaging and inversion algorithms (Versteeg, 1994; Lu et al., 2011; Salem et al., 2014; Shragge et al., 2019a, b). Whilst these provide valuable insights, the efforts required to build these test cases preclude the construction of large numbers of significantly different models. It is easy enough to vary petrophysical properties with fixed volumes; however varying the geometry and, in particular, the topology is time-consuming.
Implicit geological modelling is based on the calculation of scalar fields that can be iso-surfaced to retrieve stratigraphy and structure, as opposed to earlier methods that were CAD-like or based on the interpolation of data points. Recent advances in implicit modelling allow extensive geology model suites to be generated by perturbing the data inputs to the model (Caumon, 2010; Cherpeau et al., 2010; Jessell et al., 2010; Wellmann et al., 2010; Wellmann and Regenauer-Lieb, 2012; Lindsay et al., 2012, 2013a, b, 2014; Wellmann et al., 2014, 2017; Pakyuz-Charrier et al., 2018a, b, 2019) as part of studies that characterised 3D model uncertainty; however since they use a single model as the starting point for the stochastic simulations, these works do not provide a broad exploration of the range of geological geometries and relationships found in nature. Work on the automating of modelling workflows may allow us to explore the model uncertainty space more efficiently (Jessell et al., 2021).
In this study, we have created a massive open-access resource consisting of 1 million three-dimensional geological models using the Noddy modelling package (Jessell, 1981; Jessell and Valenta, 1996). These are provided as the input file that define the kinematics, together with the resulting voxel model and gravity and magnetic forward-modelled response. The models are classified by the sequence of their deformation histories, thus addressing a temporal paucity of ground truth. This resource is provided to anyone who would like to train a ML algorithm to understand 3D geology and the resulting potential-field response or to anyone wishing to test the robustness of their geophysical inversion techniques. Guo et al. (2022) used the same modelling engine to produce more than 3 million models of a more restricted range of parameters to train a ML convolutional neural network system to estimate 3D geometries from magnetic images. In this study we aim to provide a much broader range of possible geological scenarios as the starting point for a more general exploration of the geological model space.
The Noddy software has been used in the past for a range of studies due to its ease in producing “reasonable-looking” geological models with a low design or computational cost. A precursor to this study used 100 or so manually specified models as a way of training geologists in the interpretation of regional geophysical data sets by providing a range of 3D geological models and their geophysical responses (Jessell, 2002). Similarly, Clark et al. (2004) developed a suite of ore deposit models and their potential-field responses. The automation of model generation using Noddy was first explored using a genetic algorithm approach to modifying parameters as a way of inverting for potential-field geophysical data, specifically gravity and magnetics (Farrell et al., 1996). Wellmann et al. (2016) developed a modern Python interface to Noddy to allow stochastic variations of the input parameters to be analysed in a Bayesian framework. Finally Thiele et al. (2016a, b) used this ability to investigate the sensitivity of variations in spatial and temporal relationships as a function of variations in input parameters.
In this study we draw upon the ease of generating stochastic model suites to build a publicly accessible database of 1 million 3D geological models and their gravity and magnetic responses.
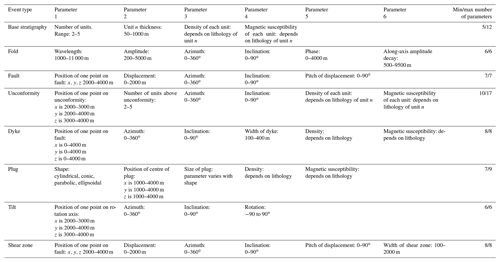
The Noddy package (Jessell, 1981; Jessell and Valenta, 1996) provides a simple framework for building generic 3D geological models and calculating the resulting gravity and magnetic responses for a given set of petrophysical properties. The 3D model is defined by superimposing user-defined kinematic events that represent idealised geological events, namely base stratigraphy (STRAT), folds (FOLD), faults (FAULT), unconformities (UNC), dykes (DYKE), plugs (PLUG), shear zones (SHEAR-ZONE) and tilts (TILT), which can be superimposed in any order, except for STRAT, which can only occur once and has to be the first event. The 3D geological models are calculated by taking the current position of a point and unravelling the kinematics (using idealised displacement equations) until we get back to the time when the infinitesimal volume of rock was formed, whether defined by the initial stratigraphy, the time of formation of a stratigraphy above an unconformity or an intrusive event. In this study, we use only the resulting voxel representation of the 3D geological models; however it is possible to produce iso-surface representations of the pre-deformation location of points in an implicit scheme. We have used this tool as it is rapid, taking under 15 s to generate voxel models with both geological and geophysical representations combined using an Intel® Xeon® Gold 6254 CPU at 3.10 GHz, and produces “geologically plausible” models that may occur in nature. Given that the final 3D model depends on the user's choice of geological history, Noddy can be thought of as a kinematic, semantic, implicit modelling scheme.
As opposed to Wellmann et al. (2016), Thiele et al. (2016) and Guo et al. (2022), who used a Python wrapper to generate stochastic model suites, in this study we have modified the C code itself to simplify use by third parties, although the philosophy of model generation is an extension of, as well as very similar to, these earlier studies. The most significant difference is that we have added petrophysical variations by randomly selecting from a set of stratigraphic groups; see the next section.
Figure 1 shows one example model set for a STRAT–TILT–DYKE–UNC–FOLD history, consisting of a 3D visualisation looking from the NE of the voxel model, with some units rendered transparent for clarity; the top surface of the model; an E–W section at the northern face of the model looking from the south; a N–S section on the western face of the model looking from the east; and the resulting gravity and magnetic fields.
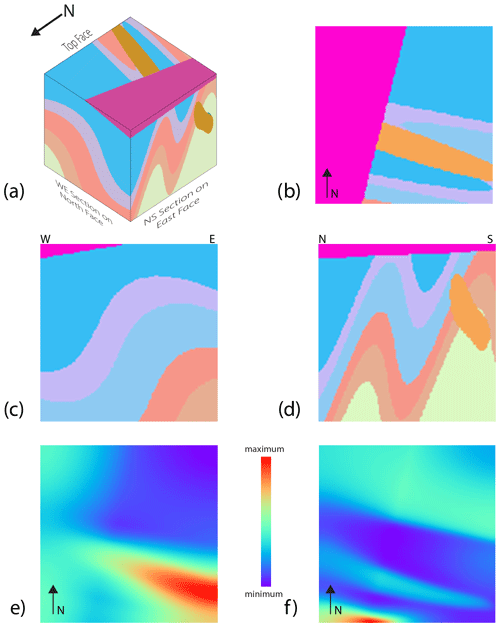
Figure 1Example model set for a STRAT–TILT–DYKE–UNC–FOLD sequence showing (a) 3D visualisation looking from the NW of the voxel model, (b) the top surface of the model, (c) an E–W section at the northern face of the model looking from the south, (d) a N–S section on the western face of the model looking from the west, and the resulting (e) gravity and (f) magnetic fields. Geophysical images are all normalised to model max–min values.
In this section we describe the choices and range of values for the parameters that we have allowed to vary for our 1-million-model suite. We recognise there are other unused modes of deformation that Noddy allows that have been ignored. The selection of these parameters is based on assessing the range of parameter values that will produce suites of models that we believe will help in and not hinder addressing the challenges cited in the Introduction. For example, we limited the size of the plugs so that a single plug could not replace the geology of the entire volume of interest. In the discussion, we refer to additional event parameters that could be activated in future studies. We limited the study to five deformation events, starting with an initial horizontal stratigraphy which is always followed by tilting of the geology. The following three events are drawn randomly and independently from the event list comprised of folds, faults, unconformities, dykes, plugs, shear zones and tilts. The likelihoods of folds, faults and shear zones are double those of the other events as we found, based on a qualitative assessment, that they had a bigger impact of changing the overall 3D geology, and hence we wished to sample more of these events. This means we can have 73=343 distinct deformation histories, although the specific parameters for each event can also vary, so the actual dimensionality of the system is much higher. For clarification, the 1 million models are not the result of a combinatorial approach but of 1 million independent draws using a Monte Carlo (MC) sampling of the model space. Whilst a combinatorial approach may in theory explore the parameter space more uniformly, the sequence of five deformation events is so non-linear that it was reasoned that a pure MC approach would serve our purposes.
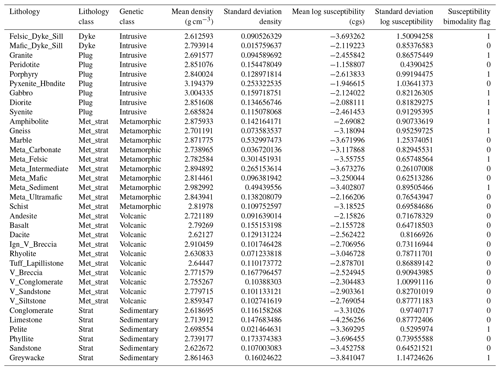
The initial stratigraphy, as well as new, above-unconformity stratigraphies, is defined to randomly have between two and five units to keep the systems relatively simple, but this could of course be increased if desired. The lithology of each unit in a stratigraphy is chosen to be coherent with the specific event and other units in the same sequence so that we do not, for example, mix high-grade metamorphic lithologies and un-metamorphosed mudstones in the same stratigraphic series (Table 2), nor do we assign the petrophysical properties of a sandstone to an intrusive plug. Once a lithology is chosen, the density and magnetic susceptibility are randomly sampled from a table defining the Gaussian distribution of properties (linear for density, log-linear for magnetic susceptibility) for that rock type. In the case of densities this may result in occasional negative values; however since the gravity field is only sensitive to density contrasts, this does not invalidate the calculation. Some rock types have bimodal petrophysical properties to reflect real-world empirical observations, so we draw from a Gaussian mixture in these cases. The petrophysical data are drawn from aggregated statistics (mean and standard deviation of one or two peaks) of the approximately 13 500-sample British Columbia petrophysical database (Geoscience BC, 2008).
The parameters which can be varied for each type of event, together with the range of these parameters, are shown in Table 1. These parameters can be grouped by the shape, position, scale and orientation of the events, and for a five-stage deformation history, the random selection is required of a minimum of 23 parameters for a STRAT–TILT–TILT–TILT–TILT model and up to 69 parameters for a STRAT–TILT–UNC–UNC–UNC model where each stratigraphy has five units. Apart from the petrophysical parameters, all other parameters are randomly sampled from a uniform distribution.
Table 2Simplified petrophysical values derived from British Columbia database (Geoscience BC, 2008). Values are randomly sampled from Gaussian distributions defined by the mean and standard deviation of density and log magnetic susceptibility. For lithologies with bimodal magnetic susceptibilities (flag of 1), mixed sampling is based on offsetting the means by ±0.75 orders of magnitude, which approximates the variations seen in nature. V_ is short for volcanic.
Any subset of the geology can be calculated for any sub-volume of an infinite Cartesian space using Noddy, but we limit ourselves to a km volume of interest in this study. Similarly, although the geology within this volume can be calculated at an arbitrary resolution, we have chosen to sample it using equant 20 m voxels as this is well below the typical resolved measurement scale for these types of data when collected in the field.
Geophysical forward models were calculated using a Fourier domain formulation using reflective padding to minimise (but not remove) boundary effects. The forward gravity and magnetic field calculations assume a flat top surface with a 100 m sensor elevation above this surface and the Earth's magnetic field with vertical inclination, zero declination and an intensity of 50 000 nT.
The 73 possible event histories produce 343 possible sequences, which averages to 2915 models per sequence. Given the imposed bias towards folds, faults and shear zones, different event sequences were more or less likely to be found in the 1-million-model suite. The high-probability event sequences (e.g. FAULT–SHEAR ZONE–FOLD) produced 8245 models, while the low-probability event sequences (e.g. UNC–TILT–PLUG) produced only 905 models. The different combinations produced plateaux in the number of models calculated, giving event sequence frequencies at around 1000, 2000, 4000 and 8000 depending on the number (0, 1, 2 and 3 respectively) of events in the sequence. Together these form a “Noddyverse” of 1 million 3D geological models and their gravity and magnetic responses. Figure 2 shows an arbitrarily selected suite of 100 models as a 10×10 grid showing the top surface and two sections of the model as in Fig. 1, together with the resulting gravity and magnetic fields, to show the variability in the results.
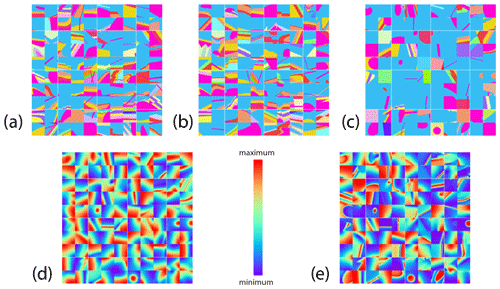
Figure 2Example models for 100 randomly selected models drawn from the 1-million-model suite showing (a) the top surface of the model, (b) an E–W section at the northern face of the model looking from the south, (c) a N–S section on the western face of the model looking from the west, and the resulting (d) gravity and (e) magnetic fields. Geophysical images are all normalised to model max–min values.
The same logic of using millions of Noddy models was first applied by generating a massive 3D model training set and used to invert real-world magnetic data (Guo et al., 2022). That study used a model suite consisting of only FOLD, FAULT and TILT events and only one of each to predict 3D geology using a convolutional neural network (CNN). This approach corresponds to a use case where prior geological knowledge of the local geological history has been used to limit the model search space, and formal expert elicitation could provide an important precursor step to support the generation of sensible and tractable problems. In addition to the CNN training demonstrated by Guo et al. (2022), we can envisage three broad categories of studies that could build upon the 3D model database we present here.
-
Studies into the uniqueness of 3D models relative to geological event histories. The principal question here is whether any form of classification of the patterns seen in the geophysical fields, perhaps including mapping of the surface, can be used to recover the event sequence or event parameters. Feature extraction techniques are well known for supporting image classification and clustering, so using the same principles, can we identify unique clusters of forward models from the Noddyverse, and do these clusters then correspond to distinct histories? Likewise, can we train a classifier with extracted features from the forward models of the gravity and magnetic responses which can then successfully identify models with similar or the same histories? Three broad aspects need to be considered here: (1) the feature extraction method, (2) the choice of pre-processing methods for dimensionality reduction (self-organising maps, principal component analysis, kernel principal component analysis, t-distributed stochastic neighbour embedding, etc.), and (3) the clustering (k-means, hierarchical methods, DBSCAN/OPTICS) or classification methods (random forests, support vector machines, linear classifiers).
A study of geophysical image variability using a simple 2D correlation or maximal information coefficient between pairs of images of different histories would be illuminating. Do we have images which are the same as each other (or at least very similar and within the noise tolerance of the geophysical fields) but belong to very different histories? If these exist, the ambiguity of the histories can be examined, and we then know where we would expect poor performance from ML techniques which rely on easily discriminated images. The systems of equations characterising geophysical inverse problems often have a non-unique solution. In ML research, if we only use magnetic data or gravity data for inversion, we will be troubled by the non-uniqueness of the solution. However, because we have both gravity data and magnetic data, we can extract features from multi-source heterogeneous data at the same time and then classify or regress them after feature fusion. This could greatly reduce the influence of the non-unique solution. Having a large set of models will allow clustering of models according to their geophysical response and identifying subsets of geological models that are geophysically equivalent and cannot be distinguished using geophysical data. The analysis of diversity of such subsets of models will give an estimate of the severity of non-uniqueness and allow the derivation of posterior statistical indicators conditioned by geological plausibility.
-
Comparison between training schemes of ML systems. We see potential applications of deep learning techniques (e.g. convolutional neural network and generative adversarial networks) where the series of models we propose may also be complemented by other data sets. In this broad topic we would seek to understand which ML techniques are suitable and effective in mapping geophysical data back to the geology or geological parameters. We can see potential for investigating which techniques minimise the number of data necessary to obtain a good constraint; i.e. what are the model structures that most successfully capture geological expert knowledge? This could be framed as an open challenge to allow different groups to use their preferred approach to the inversion problem.
-
Validation of the robustness of geophysical inversion schemes. As previously mentioned, one of the limitations to validating geophysical inversion schemes is the small number of test models available, with the resulting danger that the inversion parameters are tuned to the specifics of the test model, rather than being generally applicable. The Noddyverse model suite allows researchers to test their inversions against a wide range of scenarios. It will also allow the examination of the validity and generality of hypotheses at the foundation of several integration and joint inversion procedures. One well-known example is the underlying assumption that the underlying models vary spatially in some coherent fashion (Haber and Oldenburg, 1997; Gallardo and Meju, 2004; Giraud et al., 2021; Ogarko et al., 2021). The analysis of geophysically equivalent models will also enable us to estimate how significantly joint inversion or interpretation can reduce the non-uniqueness of the solution, with the potential to identify families of geological scenarios more suited to joint inversion than others. It is obvious that some 3D geological models will be geologically more complex than others and that some could be used for the benchmark not only of deterministic geophysical inversion of gravity and magnetic data but also of other geophysical techniques relying on wave phenomena. The data set presented here contains all required ingredients for the training of ML surrogate models for general applications and is similar in spirit to the work of Athens and Caers (2021), who train a surrogate ML model on realisations already sampled by Monte Carlo simulation and show that it is very advantageous computationally. While the work they present is performed in 2D, it is safe to assume that this may hold in 3D, which enables another avenue for further use of the Noddyverse.
In this study we have produced a ML training data set that attempts to address six recognised limitations of applying ML to geoscientific data sets, namely spatio-temporal structure; high dimensionality; small sample size; paucity of ground truth; multi-resolution data; and noise, incompleteness and uncertainty in data. Contrary to usual practice, the work for the generation of a comprehensive suite of geological models did not depend on the manual labelling of data. We relied solely on geoscientific theory and principles while remaining computationally efficient. While realistic-looking suites of geological models have been generated using generative adversarial networks (Zhang et al., 2019), these generally represent a limited range of geological scenarios and lack extensive training samples.
6.1 Spatio-temporal structure
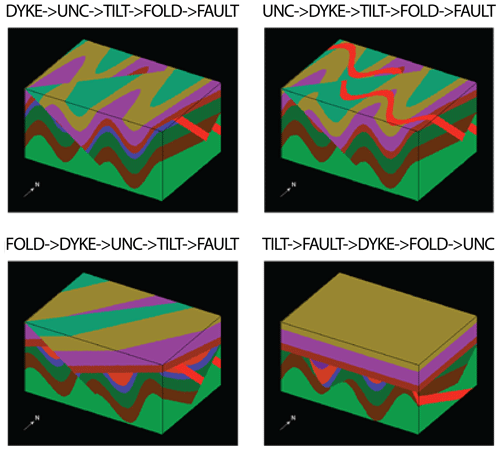
Noddy is by design a spatio-temporal modelling engine that uses a geological history to generate a model. Simple variations in the ordering of three events following two fixed events (STRAT and TILT), even with fixed parameters, quickly demonstrate the importance of relative time ordering to final model geometry (Fig. 3). While Noddy is limited to simple sequential events, nature presents geological processes to be coeval (such as syn-depositional faulting) or partially overlapping, resulting in complex spatio-temporal relationships (Thiele et al., 2016a). Nonetheless, re-ordering only sequential events still produces a vast array of plausible geometries and indicates the enormity of the model space and the necessity of efficient methods to explore them.
6.2 High dimensionality
We have limited ourselves to five deformation events in this study and no more than five units in any one stratigraphy. These decisions were based on an idea to “keep it simple” whilst simultaneously allowing a great variety of models to be built. We recognise that these are somewhat arbitrary choices. We could have true randomly complex 3D histories, leading to models with, for example, nine phases of folding; however the utility of over-complicating the system is not clear and would rarely or ever be discernible in natural systems. Similarly, we limited the parameter ranges of each deformation event, again on the basis that the ranges chosen made models that are more interesting. For example, there did not seem much interest in having folds with very large wavelengths or very low amplitudes, as they are equivalent to small translations of the geology and would translate in the geophysical measurements into a regional trend that is often approximated and removed from the measurements.
Noddy is capable of predicting continuous variations in petrophysical properties, including variably deformed magnetic remanence vectors and the anisotropy of susceptibility, or densities that vary away from structures to simulate alteration patterns; however we decided to limit this study to simple litho-controlled petrophysics whilst recognising the interest of studying more complex discrete–continuous systems. The indexed models could also be reused with different, simpler petrophysical variations, such as keeping constant values for each rock type. Each model comes with the history file used to generate the model, and this provides the full label for that model so that if additional information, such as the number of units in a series, is considered to be important, this can be easily extracted from the file.
6.3 Small sample size
The total number of models sounds impressive; however once we divide that number by the 343 different event sequences, we are left with between 905 and 8245 models per sequence, which, whilst still large, is by no means exhaustive. There is no fundamental problem with building 10 or 100 million models, and if this is found to be necessary to provide useful ML training data sets, we can certainly do so at the expense of an increased computation time: these models were built in around a week on a computer using 20 processor cores. We can also try to apply a metric, such as model topology, to analyse how well sampled the model space is. Thiele et al. (2016b) analysed the topology of stochastically generated Noddy models and found that after 100 models for small perturbations around a starting model, the number of new topologies dropped off rapidly. In our case we are not making small perturbations, so we could expect to require more models before the rate of production of new topologies decays, and topology is only one possible metric for comparing models.
6.4 Paucity of ground truth
The primary goal of this study was to build a large data set to provide a wide range of possible models for use in training ML systems and to test more traditional geophysical inversion systems. The models here, whilst simpler than the large test models mentioned earlier, represent to our knowledge the largest suite of 3D geological models with resulting potential-field data and tectonic history, which have their own utility. This usage applies equally well to classical geophysical inversion codes, which have traditionally been tested on only a handful of synthetic models prior to being applied to real-world data, for which there is no ground truth available.
6.5 Expert elicitation
To use this suite of models as the starting point for inversion of real-world data sets (as has been pioneered by Guo et al., 2022), we can envisage the introduction of expert elicitation methods to meaningfully constrain the model output space while acknowledging our inherent uncertainty regarding the model input space. As a probabilistic encoder of expert knowledge, formal elicitation procedures (O'Hagan et al., 2006) have contributed greatly to physical domain sciences where complex models are essential to our understanding of the underlying processes. From climatology, meteorology and oceanography (Kennedy et al., 2008) to geology and geostatistics (Walker and Curtis, 2014, and Lark et al., 2015) to hydrodynamics and engineering (Astfalck et al., 2018, 2019), the central role of expert elicitation is being increasingly recognised. The complexity and parameterisations of geophysical models, as well as the expert knowledge that resides within the geophysical community, suggest this domain should be no different. It is worth noting that the choice of parameter bounds used to define the 1-million-model suite in this article is itself an informal expression of expert elicitation.
Once a targeted structure is reasonably well characterised, the approach taken by Guo et al. (2021) of thoroughly exploring a narrow search space becomes possible. Unfortunately, in many parts of the world there is no outcrop available due to tens to hundreds of metres of cover. In these scenarios, it makes sense to start with a broader search for possible 3D models that may match the observed gravity or magnetic response, given their inherent ambiguity. We can imagine a hierarchical approach where a subset of the 1 million models is identified as possible causative structures, and then these are accepted or rejected based on the geologist's prior knowledge, and the accepted models are then used as the basis for a focussed parameter exploration. In addition, within the 1-million-model suite, it is currently possible to filter the models based on event ordering, and with minor modifications to the code, it would be possible to filter by any parameter, such as fold wavelength.
6.6 Extending to the model suite
In the future we may need a better representation of the “real-world” 3D model space, specifically by doing the following:
-
Include more parameters. The inclusion of more parameters from Noddy, especially for parameters such as fold profile variation or alteration near structures would allow petrophysical variation within units. This would help to address the Karpatne et al. (2017) challenge of objects with amorphous boundaries. These are capabilities that exist within Noddy but are not used in this study.
-
Allow more events. Allowing more events would increase the range of outcomes. We arbitrarily restricted ourselves to two starting events (STRAT and TILT) followed by three randomly chosen events, and an extension to the model suite could consider any number of events in the sequence.
-
Include magnetic remanence and anisotropy effects. At present we only model scalar magnetic susceptibility, but the Noddy modelling engine can calculate variable remanence and anisotropic magnetic susceptibility as well.
-
Allow linked deformation events. At the moment every event is independently defined; however we could allow parallel fault sets or dyke swarms, situations which commonly occur in nature.
-
Predict different types of geophysical fields. For example, the SimPEG package (Cockett et al., 2015) could easily be linked to this system to predict electrical fields (Cockett et al., 2015).
-
Model larger volumes. Modelling larger volumes would be an improvement as large or deep features cannot currently be modelled due to the 4 km model dimensions.
-
Build more models. We in no way believe we have explored the range of possible models in the present model suite, and if we include more events or more complex event definitions, we will certainly have to generate many more models, perhaps orders of magnitude more, in order to provide robust training suites and inversion scenarios.
-
Add noise. Adding noise to the petrophysical models and/or the resulting geophysical responses would help to address the Karpatne et al. (2017) challenge of noise, incompleteness and uncertainty in data. Incompleteness can be addressed by removing parts of the geophysical data and does not require new models to be built. Similarly, the challenge of multi-resolution data in geoscience could be addressed by subsampling parts of or all existing geophysical outputs.
-
Include topographic effects. In this study, we have ignored the effect of topography on the models, although again this could be included in the future, as it is supported by Noddy.
We also need to be clear that a model built in Noddy is not capable of predicting all geological settings, as all Noddy models have plausible geology, but not all plausible geology can be modelled by Noddy. To improve this situation, we would need to improve the modelling engine itself. Similarly, the logic of trying to predict geology from geophysical data sets in this study is only partially fulfilled: the geometry comes from geological events' sequences, but identical geometries can be produced by different event sequences.
A DOI (https://doi.org/10.5281/zenodo.4589883) provides access to a GitHub repository which contains the following elements (Jessell, 2021):
-
the source code (C language) for the version of Noddy adapted to producing random models;
-
a readme.md file with a link to the windows version of the Noddy software, plus a link to 343 .tar files, 1 for each event history ordering of the model suite;
-
a Jupyter notebook (Python code) for sampling from and unpacking the models;
-
a link in the same readme.md file to the equivalent https://mybinder.org (last access: 27 January 2022) version of the notebook so that no code installation is required to sample from and view the model suite – https://mybinder.org/v2/gh/Loop3D/noddyverse/HEAD?labpath=noddyverse-remote-files-1M.ipynb (last access: 27 January 2022).
All codes and data are released under the MIT License.
This study represents our first steps in producing geologically reasonable training sets for ML and geophysical inversion applications. We have used Noddy to generate a very large, open-access 1-million-model set of 3D geology and resulting gravity and magnetic models as ML training sets. These training sets can also be used as test cases for gravity and/or magnetic inversions. The work presented here may be a first step to overcoming some of the fundamental limitations of applying these techniques to natural geoscientific data sets.
MJ wrote the original and modified Noddy software, ran the experiments, and wrote the Python software for visualising the models. JG and YL were involved in conceptualisation and manuscript preparation. ML, JG and GP were involved in the conceptualisation, as well as in co-writing the Introduction and Discussion sections of the paper. VO, RS and EC were involved in developing and co-writing the Introduction and Discussion sections of the manuscript.
The contact author has declared that neither they nor their co-authors have any competing interests.
Publisher's note: Copernicus Publications remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
We acknowledge the support from the Loop consortia. This is MinEx CRC Document 2021/52. We would like to thank AARNet for supporting this work by hosting the 500 GB model suite at CloudStor.
This research has been supported by the Australian Research Council (grant nos. LP170100985, DE190100431 and IC190100031), the Mineral Exploration Cooperative Research Centre and the National Natural Science Foundation of China (grant no. 41671404).
This paper was edited by Jens Klump and reviewed by Jiajia Sun and one anonymous referee.
Astfalck, L., Cripps, E., Gosling, J. P., Hodkiewicz, M., and Milne, I.: Expert elicitation of directional metocean parameters, Ocean Eng., 161, 268–276, 2018.
Astfalck, L., Cripps, E., Gosling, J. P., and Milne, I.: Emulation of vessel motion simulators for computationally efficient uncertainty quantification, Ocean Eng., 172, 726–736, 2019.
Athens, N. and Caers, J.: Stochastic Inversion of Gravity Data Accounting for Structural Uncertainty, Math. Geosci., https://doi.org/10.1007/s11004-021-09978-2, 2021.
Caumon, G.: Towards stochastic time-varying geological modeling, Math. Geosci., 42, 555–569, 2010.
Cherpeau, N., Caumon, G., Caers, J., and Levy, B. E.: Method for Stochastic Inverse Modeling of Fault Geometry and Connectivity Using Flow Data, Math. Geosci., 44, 147–168, 2012.
Clark, D. A., Geuna, S., and Schmidt, P. W.: Predictive magnetic exploration models for porphyry, Epithermal and iron oxide copper-gold deposits: Implications for exploration, Short course manual for AMIRA p700 project, available at: https://confluence.csiro.au/download/attachments/26574957/Clark%20etal%202004%20P700%20CSIRO%201073Rs.pdf?version=2andmodificationDate=1460597746010andapi=v2https://confluence.csiro.au/download/attachments/26574957/Clark%20etal%202004%20P700%20CSIRO%201073Rs.pdf?version=2andmodificationDate=1460597746010andapi=v2 (last access: 27 January 2022), 2004.
Cockett, R., Lindsey, S. K., Heagy, J., Pidlisecky, A., and Oldenburg, D. W.: SimPEG: An open-source framework for simulation and gradient based parameter estimation in geophysical applications, Comput. Geosci., 85, 142–154, 2015.
Dramsch, J. S.: 70 years of machine learning in geoscience in review, Adv. Geophys., 61, 1–55, 2020.
Farrell, S. M., Jessell, M. W., and Barr, T. D.: Inversion of Geological and Geophysical Data Sets Using Genetic Algorithms, Society of Exploration Geophysicists Extended Abstract, 1404–1406, 1996.
Gallardo, L. A. and Meju, M. A.: Joint two-dimensional DC resistivity and seismic travel time inversion with cross-gradients constraints, J. Geophys. Res., 109, B03311, https://doi.org/10.1029/2003JB002716, 2004.
Geoscience BC: Development and Application of a Rock Property Database for British Columbia, Geoscience BC Project Report 2008-9, Geoscience BC [dataset], 66 pp., available at: https://catalogue.data.gov.bc.ca/dataset/rock-properties-database (last access: 27 January 2022), 2008.
Giraud, J., Ogarko, V., Martin, R., Jessell, M., and Lindsay, M.: Structural, petrophysical, and geological constraints in potential field inversion using the Tomofast-x v1.0 open-source code, Geosci. Model Dev., 14, 6681–6709, https://doi.org/10.5194/gmd-14-6681-2021, 2021.
Guo, J., Li, Y., Jessell, M., Giraud, J., Li, C., Wu, L., Li, F., and Liu, S.: 3D Geological Structure Inversion from Noddy-Generated Magnetic Data Using Deep Learning Methods, Comput. Geosci., 149, 104701, https://doi.org/10.1016/j.cageo.2021.104701, 2021.
Haber, E. and Oldenburg, D. W.: Joint Inversion: A Structural Approach, Inverse Problems, 13, 63–77, https://doi.org/10.1088/0266-5611/13/1/006, 1997.
Jessell, M., Ogarko, V., de Rose, Y., Lindsay, M., Joshi, R., Piechocka, A., Grose, L., de la Varga, M., Ailleres, L., and Pirot, G.: Automated geological map deconstruction for 3D model construction using map2loop 1.0 and map2model 1.0, Geosci. Model Dev., 14, 5063–5092, https://doi.org/10.5194/gmd-14-5063-2021, 2021.
Jessell, M. W.: NODDY – An interactive map creation package, Unpublished MSc, University of London, 1981.
Jessell, M. W.: An atlas of structural geophysics II, Journal of the Virtual explorer, 5, available at: https://virtualexplorer.com.au/journal/2001/05 (last access: 27 January 2022), 2002.
Jessell, M. W.: Loop3D/noddyverse: Noddyverse 1.0.1, Zenodo [data set, code], https://doi.org/10.5281/zenodo.4589883, 2021.
Jessell, M. W. and Valenta, R. K.: Structural Geophysics: Integrated structural and geophysical mapping, in: Structural Geology and Personal Computers, edited by: DePaor, D. G., Elsevier Science Ltd, Oxford, 542 pp., 1996.
Jessell, M. W., Ailleres, L., and Kemp, A. E.: Towards an integrated inversion of geoscientific data: What price of geology?, Tectonophysics, 490, 294–306, 2010.
Karpatne, A., Ebert-Uphoff, I., Ravela, S., Ali Babaie, H., and Kumar, V.: Machine Learning for the Geosciences: Challenges and Opportunities, IEEE T. Knowl. Data En., 31, 1544–1554, https://doi.org/10.1109/TKDE.2018.2861006, 2017.
Kennedy, M., Anderson, C., O'Hagan, A., Lomas, M., Woodward, I., Gosling, J. P., and Heinemeyer, A.: Quantifying uncertainty in the biospheric carbon flux for England and Wales, J. Roy. Stat. Soc. Ser. A, 171, 109–135, 2008.
Kollias, D. and Zafeiriou, S.: Expression, affect, action unit recognition: Aff-wild2, multi-task learning and arcface, British Machine Vision Conference (BMVC), arXiv [preprint], arXiv:1910.04855, 2019.
Lark, R. M., Lawley, R. S., Barron, A. J. M., Aldiss, D. T., Ambrose, K., Cooper, A. H., Lee, J. R., and Waters, C. N.: Uncertainty in mapped geological boundaries held by a national geological survey: eliciting the geologists' tacit error model, Solid Earth, 6, 727–745, https://doi.org/10.5194/se-6-727-2015, 2015.
Li, Y. and Oldenburg, D. W.: 3-D inversion of gravity data, Geophysics, 63, 109–119, 1998.
Lindsay, M., Ailleres, L., Jessell, M. W., de Kemp, E., and Betts, P. G.: Locating and quantifying geological uncertainty in three-dimensional models: Analysis of the Gippsland Basin, Southeastern Australia. Tectonophysics, 546–547, 10–27, 2012.
Lindsay, M., Perrouty, S., Jessell, M. W., and Ailleres, L.: Inversion and geodiversity: Searching model space for the answers, Math. Geosci., 46, 971–1010, 2014.
Lindsay, M. D., Jessell, M. W., Ailleres, L., Perrouty, S., de Kemp, E., and Betts, P. G.: Geodiversity: Exploration of 3D geological model space, Tectonophysics, 594, 27–37, 2013a.
Lindsay, M. D., Perrouty, S., Jessell, M. W., and Ailleres, L.: Making the link between geological and geophysical uncertainty: Geodiversity in the Ashanti Greenstone Belt, Geophys. J. Int., 195, 903–922, 2013b.
Lu, S., Whitmore, N. D., Valenciano, A. A., and Chemingui, N.: Imaging of primaries and multiples with 3D SEAM synthetic, SEG Technical Program Expanded Abstracts, 3217–3221, https://doi.org/10.1190/1.3627864, 2011.
Ogarko, V., Giraud, J., Martin, R., and Jessell, M.: Disjoint interval bound constraints using the alternating direction method of multipliers for geologically constrained inversion: Application to gravity data, Geophysics, 86, G1–G11, https://doi.org/10.1190/geo2019-0633.1, 2021.
O'Hagan, A., Buck, C. E., Daneshkhah, A., Eiser, J. R., Garthwaite, P. H., Jenkinson, D. J., Oakley, J. E., and Rakow, T.: Uncertain judgements: Eliciting experts' probabilities, 1st edn., John Wiley and Sons, https://doi.org/10.1002/0470033312, 2006.
Pakyuz-Charrier, E., Giraud, J., Ogarko, V., Lindsay, M., and Jessell, M.: Drillhole uncertainty propagation for three-dimensional geological modelling using Monte Carlo, Tectonophysics, 747–748, 16–39, https://doi.org/10.1016/j.tecto.2018.09.005, 2018a.
Pakyuz-Charrier, E., Lindsay, M., Ogarko, V., Giraud, J., and Jessell, M.: Monte Carlo simulation for uncertainty estimation on structural data in implicit 3-D geological modeling, a guide for disturbance distribution selection and parameterization, Solid Earth, 9, 385–402, https://doi.org/10.5194/se-9-385-2018, 2018b.
Pakyuz-Charrier, E., Jessell, M., Giraud, J., Lindsay, M., and Ogarko, V.: Topological analysis in Monte Carlo simulation for uncertainty propagation, Solid Earth, 10, 1663–1684, https://doi.org/10.5194/se-10-1663-2019, 2019.
Salem, A., Green, C., Cheyney, C., Fairhead, J. D., Aboud, E., and Campbell, S.: Mapping the depth to magnetic basement using inversion of pseudogravity, application to the Bishop model and the Stord Basin, northern North Sea, Interpretation 2, 1M-T127, https://doi.org/10.1190/INT-2013-0105.1 , 2014.
Shragge, J., Bourget, J., Lumley, D., and Giraud, J.: The Western Australia Modeling (WAMo) Project. Part I: Geomodel Building, Interpretation, 7, 1–67, 2019a.
Shragge, J., Lumley, D., Bourget, J., Potter, T., Miyoshi, T., Witten, B., Giraud, J., Wilson, T., Iqbal, A., Emami Niri, M., and Whitney, B.: The Western Australia Modeling (WAMo) Project. Part 2: Seismic Validation, Interpretation, 7, 1–62, 2019b.
Thiele, S. T., Jessell, M. W., Lindsay, M., Ogarko, V., Wellmann, F., and Pakyuz-Charrier, E.: The Topology of Geology 1: Topological Analysis, J. Struct. Geol., 91, 27–38, 2016a.
Thiele, S. T., Jessell, M. W., Lindsay, M., Wellmann, F., and Pakyuz-Charrier, E.: The Topology of Geology 2: Topological Uncertainty, J. Struct. Geol., 91, 74–87, 2016b.
Van der Baan, M. and Jutten, C.: Neural networks in geophysical applications, Geophysics, 65, 1032–1047, 2000.
Versteeg, R.: The Marmousi experience: Velocity model determination on a synthetic complex data set, The Leading Edge, 5, 927–936, 1994.
Walker, M. and Curtis, A.: Eliciting spatial statistics from geological experts using genetic algorithms, Geophys. J. Int., 198, 342–356, https://doi.org/10.1093/gji/ggu132, 2014.
Wellmann, F. and Regenauer-Lieb, K.: Uncertainties have a meaning: Information entropy as a quality measure for 3-D geological models, Tectonophysics, 526, 207–216, 2012.
Wellmann, F., Horowitz, F. G., Schill, E., and Regenauer-Lieb, K.: Towards incorporating uncertainty of structural data in 3D geological inversion, Tectonophysics, 490, 141–151, 2010.
Wellmann, F., de la Varga, M., Murdie, R. E., Gessner, K., and Jessell, M. W.: Uncertainty estimation for a geological model of the Sandstone greenstone belt, Western Australia – Insights from integrated geological and geophysical inversion in a Bayesian inference framework, Geological Society, London, Special Publications, 453, 41–52, 2017.
Wellmann, J. F., Lindsay, M., Poh, J., and Jessell, M.: Validating 3-D Structural Models with Geological Knowledge for meaningful Uncertainty Evaluations, Enrgy. Proced., 59, 374–381, 2014.
Wellmann, J. F., Thiele, S. T., Lindsay, M. D., and Jessell, M. W.: pynoddy 1.0: an experimental platform for automated 3-D kinematic and potential field modelling, Geosci. Model Dev., 9, 1019–1035, https://doi.org/10.5194/gmd-9-1019-2016, 2016.
Zhang, T.-F., Tilke, P., Dupont, E., Zhu, L.-C., Liang, L., and Bailey, W.: Generating geologically realistic 3D reservoir facies models using deep learning of sedimentary architecture with generative adversarial networks, Pet. Sci., 16, 541–549, 2019.
the answer. We present a suite of synthetic 3D geological models with their gravity and magnetic responses that allow researchers to test their methods on a whole range of geologically plausible models, thus overcoming one of the fundamental limitations of automation studies.