Long-term variations in actual evapotranspiration over the Tibetan Plateau

Actual terrestrial evapotranspiration (ET_a) is a key parameter controlling land–atmosphere interaction processes and water cycle. However, spatial distribution and temporal changes in ET_a over the Tibetan Plateau (TP) remain very uncertain. Here we estimate the multiyear (2001–2018) monthly ET_a and its spatial distribution on the TP by a combination of meteorological data and satellite products. Validation against data from six eddy-covariance monitoring sites yielded root-mean-square errors ranging from 9.3 to 14.5 mm per month and correlation coefficients exceeding 0.9. The domain mean of annual ET_a on the TP decreased slightly (−1.45 mm yr⁻¹, p<0.05) from 2001 to 2018. The annual ET_a increased significantly at a rate of 2.62 mm yr⁻¹ (p<0.05) in the eastern sector of the TP (long >90^∘ E) but decreased significantly at a rate of −5.52 mm yr⁻¹ (p<0.05) in the western sector of the TP (long <90^∘ E). In addition, the decreases in annual ET_a were pronounced in the spring and summer seasons, while almost no trends were detected in the autumn and winter seasons. The mean annual ET_a during 2001–2018 and over the whole TP was 496±23 mm. Thus, the total evapotranspiration from the terrestrial surface of the TP was 1238.3±57.6 km³ yr⁻¹. The estimated ET_a product presented in this study is useful for an improved understanding of changes in energy and water cycle on the TP. The dataset is freely available at the Science Data Bank (https://doi.org/10.11922/sciencedb.t00000.00010; Han et al., 2020b) and at the National Tibetan Plateau Data Center (https://doi.org/10.11888/Hydro.tpdc.270995, Han et al., 2020a).

1 Introduction

As the birthplace of Asia's major rivers, the Tibetan Plateau (TP), famous as the “Water Tower of Asia”, is essential to the Asian energy and water cycles (Immerzeel et al., 2010; Yao et al., 2012). Along with increasing air temperature, evidence from the changes in precipitation, runoff, and soil moisture indicates that the hydrological cycle of the TP has been intensified during the past century (Yang et al., 2014). Consuming around two-thirds of global terrestrial precipitation, evapotranspiration (ET) is a crucial component that affects the exchange of water and energy between the land surface and the atmosphere (Oki and Kanae, 2006; Fisher et al., 2017). ET is also a key factor modulating regional and global weather and climate. As one essential connecting component between the energy budget and the water cycle in the terrestrial ecosystems (Xu and Singh, 2005), ET and its variations have been drawing more attention worldwide (Xu and Singh, 2005; Li et al., 2014; T. Zhang et al., 2018; Yao et al., 2019; G. Wang et al., 2020). Total evaporation from large lakes of the TP has been quantitatively estimated recently (B. Wang et al., 2020); however, the terrestrial ET on the TP and its spatial and temporal changes remain very uncertain.

Many studies have tried to evaluate ET's temporal and spatial variability across the TP using various methods. The pan evaporation (E_pan), which represents the amount of water evaporated from an open circular pan, is the most popular observational data source of ET. Long time series of E_pan are often available with good comparability among various regional measurements. Thus, it has been widely used in various disciplines, e.g., meteorology, hydrology, and ecology. Several studies have revealed the trend of E_pan on the TP (Zhang et al., 2007; Liu et al., 2011; Shi et al., 2017; C. Zhang et al., 2018; Yao et al., 2019). Although E_pan and potential ET suggest the long-term variability in ET according to the complementary relationship (CR) between E_pan and actual ET (ET_a) (Zhang et al., 2007), these measures cannot precisely depict the spatial pattern of trends in ET_a. Recently, several studies applied revised models based on the CR of ET to estimate ET_a on the TP (T. Zhang et al., 2018; Ma et al., 2019; G. Wang et al., 2020). Employing only routine meteorological observations without requiring any vegetation and soil information is the most significant advantage of CR models (Szilagyi et al., 2017). However, numerous assumptions and requirements of validations of key parameters limit the application and performance of CR models over different climate conditions. The application of eddy-covariance (EC) technologies in the past decade has dramatically advanced our understanding of the terrestrial energy balance and ET_a over various ecosystems across the TP. However, the fetch of the EC observation is on the order of hundreds of meters, thus impeding the ability to capture the plateau-scale variations in ET_a. Therefore, finding an effective way to advance the estimation of ET_a on the TP is of great importance.

Satellite remote sensing (RS) provides temporally frequent and spatially contiguous measurements of land surface characteristics that affect ET, for example, land surface temperature, albedo, and vegetation index. Satellite RS also offers the opportunity to retrieve ET over a heterogeneous surface (Zhang et al., 2010). Multiple RS-based algorithms have been proposed. Among these algorithms, the surface energy balance system (SEBS) proposed by Su (2002) has been widely applied to retrieve land surface turbulent fluxes on the TP (Chen et al., 2013b; Ma et al., 2014; Zou et al., 2018; Zhong et al., 2019; Han et al., 2016, 2017). Chen et al. (2013b) improved the roughness length parameterization scheme for heat transfer in SEBS to expand its modeling applicability over bare ground, sparse canopy, dense canopy, and snow surfaces in the TP. An algorithm for effective aerodynamic roughness length had been introduced into the SEBS model to parameterize subgrid-scale topographical form drag (Han et al., 2015, 2017). This scheme improved the skill of the SEBS model in estimating the surface energy budget over mountainous regions of the TP. A recent advance by Chen et al. (2019) optimized five critical parameters in SEBS using observations collected from 27 sites globally, including 6 sites on the TP, and suggested that the overestimation of the global ET was substantially improved with the use of optimal parameters.

While the spatial and temporal pattern of the ET_a in the TP had been investigated in many studies (T. Zhang et al., 2018; G. Wang et al., 2020; Zhang et al., 2007), considerable inconsistencies for both trends and magnitudes of ET_a exist due to uncertainties in forcing and parameters used by various models. Thus, in this study, with full consideration of the recent developments in the SEBS model over the TP, we aim to (1) develop an 18-year (2001–2018) ET_a product of the TP, along with independent validations against EC observations; (2) quantify the spatiotemporal variability in the ET_a in the TP; and (3) uncover the main factors dominating the changes in ET_a, using the estimated product.

2 Methodology and data

2.1 Model description

The SEBS model (Su, 2002) was used to derive land surface energy flux components in the present study. The remotely sensed land surface energy balance equation is given by

$$\begin{array}{}\text{(1)}& R_{\mathrm{n}}=H+LE+G_{\mathrm{0}}.\end{array}$$

R_n is net radiation flux (W m⁻²), H is sensible heat flux (W m⁻²), LE is latent heat flux (W m⁻²), and G₀ is ground heat flux (W m⁻²). Note that this equation neglected energy stored in the canopy, energy consumption related to freeze–thaw processes of permafrost and glaciers, etc. This equation is not applicable to any condition where a phase change in water occurs, except the liquid-to-vapor phase change.

The land surface net radiation flux was computed as

$$\begin{array}{}\text{(2)}& R_{\mathrm{n}}=\left(\mathrm{1}-\mathit{\alpha }\right)\times \text{SWD}+\text{LWD}-\mathit{\epsilon }\times \mathit{\sigma }\times T_{\mathrm{s}}^{\mathrm{4}},\end{array}$$

where α is the land surface albedo derived from the Moderate Resolution Imaging Spectroradiometer (MODIS) products. Downward shortwave (SWD) and longwave (LWD) radiation was obtained from the China Meteorological Forcing Dataset (CMFD). Land surface temperature (T_s) and emissivity (ε) values were also obtained from MODIS products.

In vegetated areas the soil heat flux, G₀, was calculated from the net radiation flux and vegetation cover:

$$\begin{array}{}\text{(3)}& G_{\mathrm{0}}=R_{\mathrm{n}}\times (r_{\mathrm{c}}\times f_{\mathrm{c}}+r_{\mathrm{s}}\times (\mathrm{1}-f_{\mathrm{c}}\left)\right),\end{array}$$

where r_s and r_c are ratios of ground heat flux and net radiation for surfaces with bare soil and full vegetation, respectively. Fractional vegetation cover (f_c) was derived from the normalized difference vegetation index (NDVI). Over water surfaces (NDVI <0 and α<0.47), G₀=0.5R_n was used (Chen et al., 2013a; Gao et al., 2011). On glaciers, G₀ is negligible (Yang et al., 2011) and G₀=0.05R_n.

In the atmospheric surface layer, sensible heat flux and friction velocity were calculated based on the Monin–Obukhov similarity (Stull, 1988),

$$\begin{array}{}\text{(4)}& {\displaystyle }U={\displaystyle \frac{u_{*}}{\mathit{\kappa }}}\left[\ln \left({\displaystyle \frac{z-d_{\mathrm{0}}}{z_{\mathrm{0}\mathrm{m}}^{\mathrm{eff}}}}\right)-{\mathit{\psi }}_{\mathrm{m}}\left({\displaystyle \frac{z-d_{\mathrm{0}}}{L}}\right)+{\mathit{\psi }}_{\mathrm{m}}\left({\displaystyle \frac{z_{\mathrm{0}\mathrm{m}}^{\mathrm{eff}}}{L}}\right)\right]\text{(5)}& {\displaystyle }\begin{array}{rl}{\mathit{\theta }}_{\mathrm{0}}-{\mathit{\theta }}_{\mathrm{a}}=& {\displaystyle \frac{H}{\mathit{\kappa }{u}_{*}\mathit{\rho }{C}_p}}[\ln \left({\displaystyle \frac{z-d_{\mathrm{0}}}{z_{\mathrm{0}\mathrm{h}}^{\mathrm{eff}}}}\right)-{\mathit{\psi }}_{\mathrm{h}}\left({\displaystyle \frac{z-d_{\mathrm{0}}}{L}}\right)\\ & +{\mathit{\psi }}_{\mathrm{h}}\left({\displaystyle \frac{z_{\mathrm{0}\mathrm{h}}^{\mathrm{eff}}}{L}}\right)]\end{array}\text{(6)}& {\displaystyle }L={\displaystyle \frac{\mathit{\rho }{C}_p{u}_{*}^{\mathrm{3}}{\mathit{\theta }}_{\mathrm{v}}}{\mathit{\kappa }gH}}.\end{array}$$

U is the horizontal wind velocity at a reference height z (m) above the ground surface; θ₀ is the potential temperature at the land surface (K); θ_a is the potential temperature (K) at the reference height z; d₀ is the zero-plane displacement height (m); ρ is the air density (kg m⁻³); C_p is the specific heat for moist air (J kg^−1 ∘C⁻¹); κ=0.4 is the von Kármán's constant; u_* is the friction velocity; L is the Monin–Obukhov length (m); θ_v is the potential virtual temperature (K) at the reference height z; ψ_m and ψ_h are the stability correction functions for momentum and sensible heat transfer, respectively; and g is the gravity acceleration (m s⁻²). To account for the form drag caused by subgrid-scale topographical obstacles, effective roughness lengths for momentum ($z_{\mathrm{0}\mathrm{m}}^{\mathrm{eff}}$, m) and sensible heat ($z_{\mathrm{0}\mathrm{h}}^{\mathrm{eff}}$, m) transfer were introduced into the SEBS model by Han et al. (2017). These modifications are parameterized as follows (Grant and Mason, 1990; Han et al., 2015):

$$\begin{array}{}\text{(7)}& {\displaystyle }{\ln }^{\mathrm{2}}\left(h/\mathrm{2}{z}_{\mathrm{0}\mathrm{m}}^{\mathrm{eff}}\right)={\displaystyle \frac{{\mathit{\kappa }}^{\mathrm{2}}}{\mathrm{0.5}D\mathit{\lambda }+{\mathit{\kappa }}^{\mathrm{2}}/{\ln }^{\mathrm{2}}(h/\mathrm{2}{z}_{\mathrm{0}\mathrm{m}})}},\text{(8)}& {\displaystyle }\ln \left(h/\mathrm{2}{z}_{\mathrm{0}\mathrm{h}}^{\mathrm{eff}}+\mathrm{1}\right)=\ln \left(h/\mathrm{2}{z}_{\mathrm{0}\mathrm{h}}+\mathrm{1}\right){\displaystyle \frac{\ln (h/\mathrm{2}{z}_{\mathrm{0}\mathrm{m}}+\mathrm{1})}{\ln (h/z_{\mathrm{0}\mathrm{m}}^{\mathrm{eff}}+\mathrm{1})}},\end{array}$$

where h is the average height of the subgrid-scale roughness obstacles; λ is the average density of the subgrid-scale roughness elements calculated from digital elevation models; D is the form drag coefficient, and D=0.4 is used for the mountainous areas of the TP as suggested by Han et al. (2015); and z_0 m and z_0 h are the local-scale roughness lengths for momentum and heat transfer (m), respectively. Detailed calculations can be found in Su (2002). A revised algorithm for z_0 h developed by Chen et al. (2013b) was applied as this algorithm outperforms the original scheme of the SEBS model on the TP.

To constraint the actual evapotranspiration, the evaporative fraction was applied in the SEBS model, which is determined by taking energy balance considerations at dry and wet limiting cases. Under the dry-limit condition, the evaporation becomes zero due to the limited supply of available soil moisture, while water vapor evaporates at the potential rate under the wet-limit condition (Su, 2002). The evaporative fraction (Λ) is defined as

$$\begin{array}{}\text{(9)}& \mathrm{\Lambda }={\displaystyle \frac{LE}{R_{\mathrm{n}-G_{\mathrm{0}}}}}.\end{array}$$

After calculating evaporative fraction based on the assumption of dry and wet limits, latent heat flux was calculated by inverting Eq. (9). Finally, latent heat flux was converted to ET_a. Details are available in Su (2002) and Chen et al. (2013a). Note that the dry-wet limit assumption did not apply to frozen soil, water, snow, and ice surfaces. The latent heat flux was obtained as the residual of the surface energy balance Eq. (1) after calculating net radiation, sensible heat flux, and ground heat flux when the dry-wet limit assumption is not applicable.

2.2 Data

In situ observations, satellite-based products, and meteorological forcing data were used in this study to estimate monthly ET_a over the TP area. The CMFD, which was developed based on the released China Meteorological Administration (CMA) data (He et al., 2020), was used as model input. The CMFD covers the whole landmass of China at a spatial resolution of 0.1^∘ and a temporal resolution of 3 h. The CMFD dataset was established through the fusion of in situ observations, remote sensing products, and reanalysis datasets. In particular, the dataset benefits from the merging of the observations at about 700 CMA weather stations and by using the Global Energy and Water Cycle Experiment – Surface Radiation Budget (GEWEX-SRB) shortwave radiation dataset (Pinker and Laszlo, 1992). The GEWEX-SRB data have not been used in any other reanalysis dataset. In addition, independent datasets observed in western China, where weather stations are scarce, were used to evaluate the CMFD. This includes data collected through the Heihe Watershed Allied Telemetry Experimental Research (HiWATER) (Li et al., 2013) and the Coordinated Enhanced Observing Period (CEOP) Asia–Australia Monsoon Project (CAMP) (Ma et al., 2003). The CMFD dataset has been validated against in situ meteorological observations and compared with other reanalysis datasets on the TP, demonstrating that it is one of the best meteorological forcing datasets over the TP area (Zhou et al., 2016; Xie et al., 2017; B. Wang et al., 2020). Therefore, it is suitable for this study to drive the SEBS model. Detailed information for the CMFD dataset is listed in Table 1.

Table 1 Input datasets used in this study. Note that DEM stands for digital elevation model, MOD11C3 is the short name of the MODIS/Terra land surface temperature and emissivity monthly L3 global products, MOD09CMG is the short name of the MODIS/Terra surface reflectance daily L3 global products, MOD13C2 is the short name of the MODIS/Terra vegetation indices' monthly L3 global products, ASTER GDEM stands for the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) global DEM (GDEM), GLAS stands for the Geoscience Laser Altimeter System, and SPOT stands for the Systeme pour l’Observation de la Terre sensor.

MODIS monthly land surface products, including land surface temperature and emissivity, land surface albedo, and vegetation index, provide land surface conditions for the SEBS model. Detailed information on MODIS land surface variables is listed in Table 1. The values of land surface variables in the MODIS monthly products are derived by compositing and averaging the values from the corresponding month of MODIS daily files. Validations of MODIS land surface temperature and albedo against in situ observations on the TP suggest a high quality of MODIS land surface products with low biases and small root-mean-square errors (Chen et al., 2014; Wang et al., 2004; Ma et al., 2011).

In situ EC data observed at six flux stations on the TP were used to validate model results. Locations of the six observation sites are illustrated in Fig. 1, and detailed descriptions for these six sites are shown in Table 2. The instrumental setup at each site consists of an EC system comprising a sonic anemometer (CSAT3, Campbell Scientific Inc) and an open-path gas analyzer (LI-7500, LI-COR); a four-component radiation flux system (CNR-1, Kipp & Zonen), installed at a height of 1.5 m; a soil heat flux plate (Hukseflux, HFP01), buried in the soil at a depth of 0.1 m; and soil moisture and temperature probes, buried at a depth of 0.05, 0.10, and 0.15 m, respectively (Han et al., 2017). The EC data were processed with the EC software package TK3 (Mauder and Foken, 2015). The main post-processing procedures of the EC raw data were as follows: spike detection, coordinate rotation, spectral loss correction, frequency response corrections (Moore, 1986), and corrections for density fluctuations (Webb et al., 1980). The ground heat flux was obtained by summing the flux value observed by the heat flux plate and the energy storage in the layer above the heat flux plate (Han et al., 2016). A more comprehensive dataset including the EC data used in this work has been published and is freely available (Ma et al., 2020).

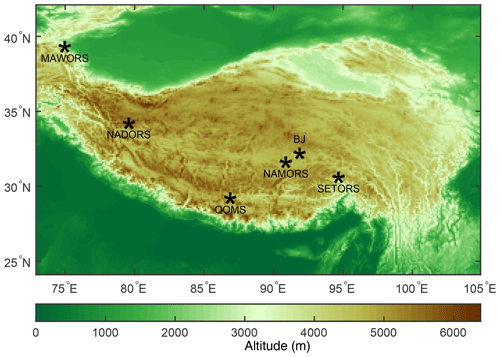
Figure 1 Locations of the six flux tower sites (marked by pentagrams) on the TP. The legend of the color map is elevation above mean sea level in meters.

Table 2 Station information.

The 3-hourly CMFD data were averaged into daily and then into monthly data to be consistent with MODIS products in terms of temporal resolution. Daily land surface albedo has been averaged into a monthly variable. MODIS land surface products and canopy height data were remapped onto the CMFD's grid. Monthly EC data and in situ meteorological observations, which are used for model validation, were generated from half-hourly variables.

2.3 Model evaluation metrics and data analysis methods

The model performance was assessed using the Pearson correlation coefficient (R), the root-mean-square error (RMSE), and the mean bias (MB) between the estimated and observed monthly ET_a at the six stations on the TP.

The least-square regression technique was used to detect the long-term linear annual trends in ET_a values. The linear model to simulate ET_a values (Y_t) against time (t) is defined as below, and the slope of the linear equation (b) is taken as the changing trend,

$$\begin{array}{}\text{(10)}& Y_t=Y_{\mathrm{0}}+bt+{\mathit{\epsilon }}_t.\end{array}$$

The Student's t test, having an n−2 degree of freedom (n is the number of samples), was used to evaluated the statistical significance of the linear trends, and only tests with a p value less than 0.05 were selected as having passed the significance test.

3 Results and discussion

3.1 Validation against flux tower observations

The SEBS-estimated ET_a was validated against EC observations at six flux stations on the TP at a monthly scale (Fig. 2). The SEBS model is capable of capturing both the magnitude and seasonal variation in the monthly ET_a signal at all the six stations. The correlation coefficients are all larger than 0.9 and have passed the significance test at the p=0.01 level. RMSE values range from 9.3 to 14.5 mm per month, with the minimum at the BJ station and the maximum at the SETORS station. The MB values are all negative except at the NADORS station, which means the SEBS model slightly underestimated ET_a values on the TP.

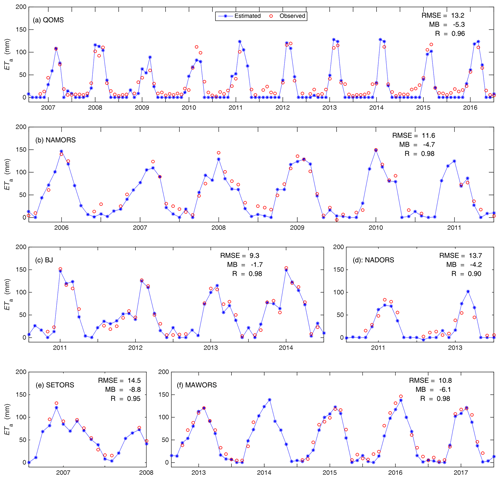
Figure 2 SEBS-estimated and EC-observed monthly ET_a at the six stations (a–f) on the TP in years when the latter observations were available. RMSE is the root-mean-square error, MB is the mean bias, and R is the correlation coefficient.

Specifically, the SEBS model performed particularly well at the short-grass sites (BJ and NAMORS), with correlation coefficients as high as 0.98 and MB values below 5.0 mm per month. At the high-grass site (SETORS) and the gravel site (QOMS), the SEBS model is capable of reproducing the EC-observed monthly ET_a with RMSE values of 14.5 and 13.2 mm per month, respectively. In addition, the underestimates of ET_a by SEBS are mostly in the dry season, when the canopy is withered. The validation at the site scale indicates that the SEBS model used in this work can be applied to a wide range of ecosystems over the TP.

3.2 Spatial distribution

There was a clear spatial pattern to the multiyear average of annual ET_a between 2001 and 2018 (Fig. 3). In general, the SEBS-estimated ET_a decreases from the southeast to the northwest of the TP, with the maximum value above 1200 mm in southeastern Tibet and the Hengduan Mountains and the minimum value less than 100 mm on the northwestern edge of the TP. In the central TP, where there are several lakes, ET_a was typically from 500 to 1000 mm. ET_a was lower than 200 mm over the high snow- and ice-bound mountainous areas, for example, over the northern slopes of the Himalaya, the Nyenchen Tanglha Mountains, and the eastern section of the Tanggula Mountains. The reason is that these snow- and ice-bound mountainous areas have a higher ability to reflect downward shortwave radiation and hence have less available energy to evaporate. On the whole, the domain-averaged multiyear mean annual ET_a over the TP is 496±23 mm. The total amount of water evapotranspired from the terrestrial surface of the TP is around 1238.3±57.6 km³ yr⁻¹, considering the area of the TP to be 2.5×10⁶ km².

Figure 3 Spatial distribution of the SEBS-estimated multiyear (2001–2018) average annual ET_a.

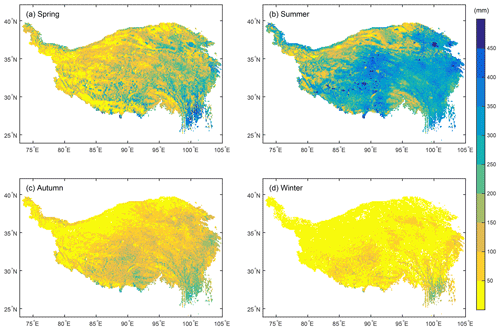
Figure 4 shows the multiyear-average spring (March, April, and May), summer (June, July, and August), autumn (September, October, and November), and winter (December, January, and February) ET_a on the TP. Generally, the distribution pattern of seasonal ET_a was comparable with that of the annual ET_a. Both seasonal and annual ET_a show a decreasing trend from the southeastern TP to the northwestern TP. Note that the spatial contrast of ET_a almost faded out in the winter season owing to a minimum in available energy and precipitation (Fig. 4d). The ET_a in spring is higher than that in autumn, except for some high mountainous areas (e.g., mountain ranges of the Himalaya and Hengduan Mountains). The spring ET_a ranges from 50 to 450 mm, while autumn ET_a ranges from 50 to 250 mm. In summer, the ET_a is larger than 250 mm in most of the TP, while the ET_a is still below 100 mm in large areas of the northwestern TP. The multiyear seasonal ET_a averaged over the whole TP is 140±10, 256±12, 84±5, and 34±4 mm for spring, summer, autumn, and winter, respectively.

Figure 4 Spatial distributions of the SEBS-estimated multiyear (2001–2018) average seasonal ET_a (millimeters per season) values over the TP. (a) Spring, (b) summer, (c) autumn, (d) winter.

3.3 Trend analysis

The trend of annual ET_a during 2001–2018 is shown in Fig. 5. Overall, an increasing trend of SEBS-simulated ET_a is dominant in the eastern TP (long >90^∘ E), while a decreasing trend is dominant in the western TP (long <90^∘ E). The trends pass the t test (p<0.05) in most parts of the areas. The decreasing trend in the western TP is pronounced and passes the t test (p<0.05). This trend is larger than −7.5 mm yr⁻¹ in most parts of the area and even larger than −10 mm yr⁻¹ in a few parts. In the eastern TP, the increasing trend is mostly between 5 and 10 mm yr⁻¹ and passes the t test (p<0.05). The ET_a trend tends to be greater along the marginal region of the northern, eastern, and southeastern TP. Along the marginal region of the southwestern TP and in the western section of the Himalaya Mountains this trend weakens.

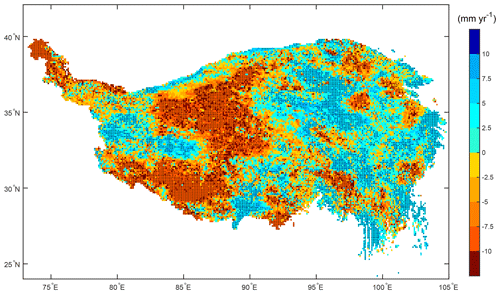
Figure 5 Spatial distribution of annual ET_a linear trend on the TP from 2001 to 2018. The stippling indicates the trends that pass the t test (p<0.05).

The trends of seasonal ET_a between 2001 and 2018 are spatially heterogeneous over the TP (Fig. 6). Decreasing trends in spring and summer are generally at a rate between −2.5 and −7.5 mm yr⁻¹, and increasing trends are generally at a rate below 5.0 and 7.5 mm yr⁻¹ in spring and summer, respectively. Areas showing decreasing ET_a tend to become larger in autumn and winter seasons. Both the decreasing and increasing trends are subdued in autumn and winter compared with that in the spring and summer seasons. Decreasing rates of ET_a in autumn and winter are generally below −2.5 mm yr⁻¹, and only a few areas have a rate larger than −2.5 mm yr⁻¹.

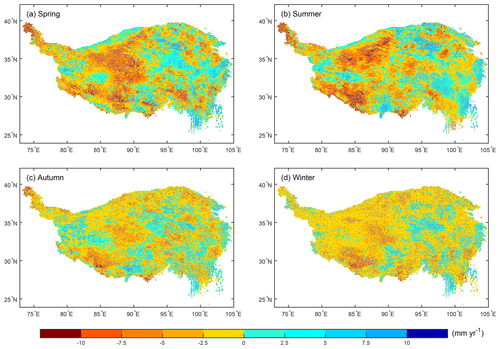
Figure 6 Spatial distributions of seasonal ET_a linear trends on the TP from 2001 to 2018: (a) annual, (b) spring, (c) summer, (d) autumn, (e) winter. The stippling indicates the trends that pass the t test (p<0.05).

Due to the contrast in the trends in the eastern and western halves of the TP, we divided the TP into two regions: the eastern TP (long >90^∘ E) and the western TP (long <90^∘ E). Trends of the ET_a anomaly averaged over the entire TP, the western TP, and the eastern TP are shown in Fig. 7a. The domain means of ET_a on the TP as a whole and in the western TP decreased at rates of −1.45 and −5.52 mm yr⁻¹, respectively. However, the ET_a in the eastern TP increased at a rate of 2.62 mm yr⁻¹. The decreasing rate of ET_a in the entire TP is influenced mainly by the significant decrease in ET_a in the western TP. Seasonally, the rates of change in ET_a over the whole TP are −0.82 mm yr⁻¹ (p<0.05) and −0.79 mm yr⁻¹ (p<0.05) in spring and summer, respectively (Fig. 7b). However, in autumn and winter the ET_a changes at a rate of 0.10 and 0.06 mm yr⁻¹, respectively, and does not pass the t test (p<0.05). ET_a in the spring and summer seasons accounts for 75.7 % of the annual ET_a. The variation in amplitude and changing rates in these two seasons are much larger than in the other seasons. Moreover, spatial distributions of spring and summer ET_a trends are close to that of the annual ET_a trend (Fig. 6). Thus, changes in ET_a in the spring and summer dominate the variations in ET_a in the whole year.

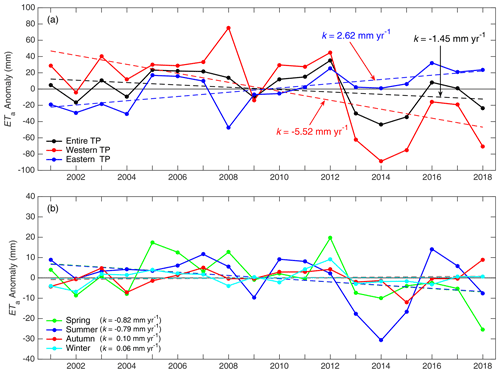
Figure 7 Anomalies of the domain-averaged annual ET_a of the entire TP, the western TP (long <90^∘ E), and the eastern TP (long >90^∘ E), respectively (a). Domain-averaged seasonal ET_a anomalies over the entire TP (b). The dashed straight lines indicate linear trends during 2001–2018, and k is the slope of the straight line.

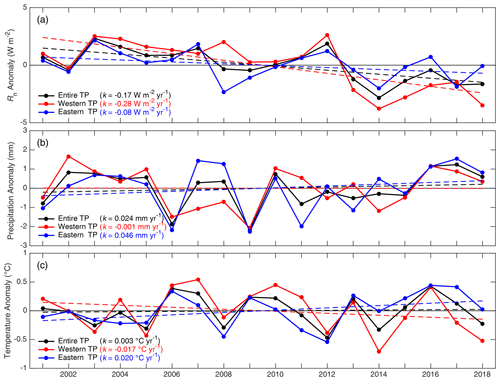
Figure 8 Domain-averaged anomalies of annual R_n (a), precipitation (b), and temperature (c) over the entire TP, the western TP (long <90^∘ E), and the eastern TP (long >90^∘ E), respectively. The dashed straight lines indicate linear trends during 2001–2018, and k is the slope of the straight line.

The decrease in ET_a over the whole TP and in the western TP during 2001–2018 can be explained by the decrease in R_n in the same time period (Fig. 8a). From 2001 to 2012, ET_a averaged over the entire TP increased slightly and then decreased dramatically from 2012, reaching a minimum in 2014. The significant decrease in ET_a between 2012 and 2014 was due to the rapid decline in the R_n (Fig. 8a). In the eastern TP, ET_a increased during 2001–2018, while R_n decreased in the same period. Thus, R_n was not the dominant factor controlling the annual variations in ET_a. However, the increasing trends of both precipitation and air temperature can explain the increase in ET_a in the eastern TP during the period 2001–2018 (Fig. 8b and c). The increasing precipitation increased the water resource available for ET_a. Moreover, the increasing air temperature accelerated the melting of permafrost and glaciers on the TP. Hence, the melting water replenished the ecosystem and increased the ET_a of the eastern TP.

Although the domain-averaged trend in ET_a has been decreasing across the entire TP from 2001 to 2018, ET_a values in some areas have increased. Moreover, the changing rates also depend on the time series of ET_a. For example, the ET_a increased slightly from 2001 to 2012, while it decreased from 2001 to 2018. This demonstrates the necessity to evaluate the spatial distribution of changing trends in ET_a and utilize long time series to investigate the trends in ET_a over the TP.

4 Data availability

The dataset presented and analyzed in this article has been released and is available for free download from the Science Data Bank (https://doi.org/10.11922/sciencedb.t00000.00010, Han et al., 2020b) and from the National Tibetan Plateau Data Center (https://doi.org/10.11888/Hydro.tpdc.270995, Han et al., 2020a). The dataset is published under the Creative Commons Attribution 4.0 International (CC BY 4.0) license.

5 Summary and conclusions

The SEBS-estimated ET_a is at a resolution of around 10 km, while the footprint of EC-observed ET_a values ranges from a few dozen meters to a few hundred meters. SEBS-estimated ET_a compares very well with observations at the six flux towers, showing low RMSE and MB values. These estimates were able to capture annual and seasonal variations in ET_a, despite these two datasets being mismatched in their spatial representation. Note that the energy consumption related to freeze–thaw processes and sublimation is neglected. Thus, the dataset is likely to be less reliable over the glacier and permafrost and in the winter season.

Heterogeneous land surface characteristics and nonlinear changes in atmospheric conditions resulted in heterogeneities in spatial distributions of ET_a and changes in ET_a. The SEBS-estimated multiyear (2001–2018) mean annual ET_a on the TP was 515±22 mm, resulting in approximately 1287.5±55.0 km³ yr⁻¹ of total water evapotranspiration from the terrestrial surface. Annual ET_a generally decreased from the southeast to the northwest of the TP. The maximum was over 1200 mm, in southeastern Tibet and the Hengduan Mountains, while the minimum was less than 100 mm in the northwestern marginal area of the TP. Moreover, ET_a was typically lower than 200 mm over snow- and ice-bound mountainous areas as there was limited available energy to evaporate the water.

Averaged over the entire TP, annual ET_a increased slightly from 2001 to 2012 but decreased significantly after 2012 and reached a minimum in 2014. Generally, there was a slight decreasing trend in the domain mean annual ET_a on the TP at the rate of −1.45 mm yr⁻¹ (p<0.05) from 2001 to 2018. However, trends of annual ET_a were opposite in the western and eastern TP. The annual ET_a decreased significantly in the western TP at a rate of −5.52 mm yr⁻¹ (p<0.05) from 2001 to 2018, while annual ET_a in the eastern TP increased at a rate of 2.62 mm yr⁻¹ (p<0.05) in the same period.

The spatial distributions of seasonal ET_a trends were also noticeably heterogeneous during 2001–2018. The spatial patterns of ET_a trend in spring and summer were similar to the annual changes in ET_a. ET_a decreased as well in the spring and summer seasons but at slower rates compared with the annual ET_a; however, only very weak trends were found in the autumn and winter seasons.