Marine terraces of the last interglacial period along the Pacific coast of South America (1° N–40° S)

Tectonically active coasts are dynamic environments characterized by the presence of multiple marine terraces formed by the combined effects of wave erosion, tectonic uplift, and sea-level oscillations at glacial-cycle timescales. Well-preserved erosional terraces from the last interglacial sea-level highstand are ideal marker horizons for reconstructing past sea-level positions and calculating vertical displacement rates. We carried out an almost continuous mapping of the last interglacial marine terrace along ∼ 5000 km of the western coast of South America between 1^∘ N and 40^∘ S. We used quantitatively replicable approaches constrained by published terrace-age estimates to ultimately compare elevations and patterns of uplifted terraces with tectonic and climatic parameters in order to evaluate the controlling mechanisms for the formation and preservation of marine terraces and crustal deformation. Uncertainties were estimated on the basis of measurement errors and the distance from referencing points. Overall, our results indicate a median elevation of 30.1 m, which would imply a median uplift rate of 0.22 m kyr⁻¹ averaged over the past ∼ 125 kyr. The patterns of terrace elevation and uplift rate display high-amplitude (∼ 100–200 m) and long-wavelength (∼ 10² km) structures at the Manta Peninsula (Ecuador), the San Juan de Marcona area (central Peru), and the Arauco Peninsula (south-central Chile). Medium-wavelength structures occur at the Mejillones Peninsula and Topocalma in Chile, while short-wavelength (< 10 km) features are for instance located near Los Vilos, Valparaíso, and Carranza, Chile. We interpret the long-wavelength deformation to be controlled by deep-seated processes at the plate interface such as the subduction of major bathymetric anomalies like the Nazca and Carnegie ridges. In contrast, short-wavelength deformation may be primarily controlled by sources in the upper plate such as crustal faulting, which, however, may also be associated with the subduction of topographically less pronounced bathymetric anomalies. Latitudinal differences in climate additionally control the formation and preservation of marine terraces. Based on our synopsis we propose that increasing wave height and tidal range result in enhanced erosion and morphologically well-defined marine terraces in south-central Chile. Our study emphasizes the importance of using systematic measurements and uniform, quantitative methodologies to characterize and correctly interpret marine terraces at regional scales, especially if they are used to unravel the tectonic and climatic forcing mechanisms of their formation. This database is an integral part of the World Atlas of Last Interglacial Shorelines (WALIS), published online at https://doi.org/10.5281/zenodo.4309748 (Freisleben et al., 2020).

1 Introduction

Tectonically active coasts are highly dynamic geomorphic environments, and they host densely populated centers and associated infrastructure (Melet et al., 2020). Coastal areas have been episodically affected by the effects of sea-level changes at glacial timescales, modifying the landscape and leaving behind fossil geomorphic markers, such as former paleo-shorelines and marine terraces (Lajoie, 1986). One of the most prominent coastal landforms are marine terraces that were generated during the protracted last interglacial sea-level highstand that occurred ∼ 125 kyr ago (Siddall et al., 2006; Hearty et al., 2007; Pedoja et al., 2011). These terraces are characterized by a higher preservation potential which facilitates their recognition, mapping, and lateral correlation. Furthermore, because of their high degree of preservation and relatively young age, they have been used to estimate vertical deformation rates at local and regional scales. The relative abundance and geomorphic characteristics of the last interglacial marine terraces make them ideal geomorphic markers with which to reconstruct past sea-level positions and to enable comparisons between distant sites under different climatic and tectonic settings.

The western South American coast (WSAC) is a tectonically active region that has been repeatedly affected by megathrust earthquakes and associated surface deformation (Beck et al., 1998; Melnick et al., 2006; Bilek, 2010; Baker et al., 2013). Interestingly, previous studies have shown that despite the broad spectrum of latitudinal climatic conditions and erosional regimes along the WSAC, marine terraces are scattered but omnipresent along the coast (Ota et al., 1995; Regard et al., 2010; Rehak et al., 2010; Bernhardt et al., 2016, 2017; Melnick, 2016). However, only a few studies on interglacial marine terraces have been conducted along the WSAC, primarily in specific areas where they are best expressed; this has resulted in disparate and inconclusive marine terrace measurements based on different methodological approaches and ambiguous interpretations concerning their origin in a tectonic and climatic context (Hsu et al., 1989; Ortlieb and Macharé, 1990; Hsu, 1992; Macharé and Ortlieb, 1992; Pedoja et al., 2006b, 2011; Saillard et al., 2009, 2011; Rodríguez et al., 2013). This lack of reliable data points has revealed a need to re-examine the last interglacial marine terraces along the WSAC based on standardized methodologies in order to obtain a systematic and continuous record of marine terrace elevations along the coast. This information is crucial in order to increase our knowledge of the climatic and tectonic forcing mechanisms that contributed to the formation and degradation of marine terraces in this region.

Marine terrace sequences at tectonically active coasts are landforms formed by wave erosion and/or accumulation of sediments resulting from the interaction between tectonic uplift and superposed oscillating sea-level changes (Lajoie, 1986; Anderson et al., 1999; Jara-Muñoz et al., 2015). Typically, marine terrace elevations are estimated based on the shoreline angle. The marine terrace morphology comprises a gently inclined erosional or depositional paleo-platform that terminates landward at a steeply sloping paleo-cliff surface. The intersection point between both surfaces represents the approximate sea-level position during the formation of the marine terrace, also known as shoreline angle; if coastal uplift is rapid, such uplifting abrasion or depositional surfaces may be preserved in the landscape and remain unaltered by the effects of subsequent sea-level oscillations (Lajoie, 1986).

The analysis of elevation patterns based on shoreline-angle measurements at subduction margins has been largely used to estimate vertical deformation rates and the mechanisms controlling deformation, including the interaction of the upper plate with bathymetric anomalies, the activity of crustal faults in the upper plate, and deep-seated processes such as basal accretion of subducted trench sediments (Taylor et al., 1987; Hsu, 1992; Macharé and Ortlieb, 1992; Ota et al., 1995; Pedoja et al., 2011; Saillard et al., 2011; Jara-Muñoz et al., 2015; Melnick, 2016). The shoreline angle represents a 1D descriptor of the marine terrace elevation whose measurements are reproducible when using quantitative morphometric approaches (Jara-Muñoz et al., 2016). Furthermore, the estimation of the marine terrace elevations based on shoreline angles can be further improved by quantifying their relationship with paleo sea level, also known as the indicative meaning (Lorscheid and Rovere, 2019).

In this continental-scale compilation of marine terrace elevations along the WSAC, we present systematically mapped shoreline angles of marine terraces of the last (Eemian–Sangamonian) interglacial obtained along 5000 km of coastline between 1^∘ N and 40^∘ S. In this synthesis we rely on chronological constraints from previous regional studies and compilations (Pedoja et al., 2011). For the first time we are able to introduce an almost continuous pattern of terrace elevation and coastal uplift rates at a spatial scale of 10³ km along the WSAC. Furthermore, in our database we compare tectonic and climatic parameters to elucidate the mechanisms controlling the formation and preservation of marine terraces and patterns of crustal deformation along the coast. This study was thus primarily intended to provide a comprehensive, standardized database and description of last interglacial marine terrace elevations along the tectonically active coast of South America. This database therefore warrants future research into coastal environments to decipher potential tectonic forcings with regard to the deformation and seismotectonic segmentation of the forearc; as such this database will ultimately help to decipher the relationship between upper-plate deformation, vertical motion, and bathymetric anomalies and aid in the identification of regional fault motions along pre-existing anisotropies in the South American continental plate. Finally, our database includes information on climate-driving forcing mechanisms that may influence the formation, modification, and/or destruction of marine terraces in different climatic sectors along the South American convergent margin. This new database is part of the World Atlas of Last Interglacial Shorelines (WALIS), published online at https://doi.org/10.5281/zenodo.4309748 (Freisleben et al., 2020).

2 Geologic and geomorphic setting of the WSAC

2.1 Tectonic and seismotectonic characteristics

2.1.1 Subduction geometry and bathymetric features

The tectonic setting of the convergent margin of South America is controlled by subduction of the oceanic Nazca plate beneath the South American continental plate. The convergence rate varies between 66 mm yr⁻¹ in the north (8^∘ S latitude) and 74 mm yr⁻¹ in the south (27^∘ S latitude) (Fig. 1). The convergence azimuth changes slightly from 81.7^∘ N toward 77.5^∘ N from north to south (DeMets et al., 2010). The South American subduction zone is divided into four major segments with variable subduction angles inferred from the spatial distribution of Benioff seismicity (Barazangi and Isacks, 1976; Jordan et al., 1983) (Fig. 1). The segments beneath northern and central Peru (2–15^∘ S) and beneath central Chile (27–33^∘ S) are characterized by a gentle dip of the subducting plate between 5 and 10^∘ at depths of ∼ 100 km (Hayes et al., 2018), whereas the segments beneath southern Peru and northern Chile (15–27^∘ S) and beneath southern Chile (33–45^∘ S) have steeper dips of 25–30^∘. Spatial distributions of earthquakes furthermore indicate a steep-slab subduction segment in Ecuador and southern Colombia (2^∘ S to 5^∘ N) and a flat-slab segment in NW Colombia (north of 5^∘ N) (Pilger, 1981; Cahill and Isacks, 1992; Gutscher et al., 2000; Ramos and Folguera, 2009). Processes that have been inferred to be responsible for the shallowing of the subduction slab include the subduction of large buoyant ridges or plateaus (Espurt et al., 2008), as well as the combination of the trenchward motion of thick, buoyant continental lithosphere accompanied by trench retreat (Sobolev and Babeyko, 2005; Manea et al., 2012). Volcanic activity, as well as the forearc architecture and distribution of upper-plate deformation, further emphasizes the location of flat-slab subduction segments (Jordan et al., 1983; Kay et al., 1987; Ramos and Folguera, 2009).

Several high bathymetric features have been recognized on the subducting Nazca plate. The two most prominent bathymetric features being subducted beneath South America are the Carnegie and Nazca aseismic ridges at 0 and 15^∘ S, respectively; they consist of seamounts related to hot-spot volcanism (Gutscher et al., 1999; Hampel, 2002). The 300 km wide and ∼ 2 km high Carnegie Ridge subducts roughly parallel to the convergence direction, and its geometry should have remained relatively stable beneath the continental plate (Angermann et al., 1999; Gutscher et al., 1999; DeMets et al., 2010; Martinod et al., 2016a). In contrast, the obliquity of the 200 km wide and 1.5 km high Nazca Ridge with respect to the convergence direction resulted in 500 km SE-directed migration of its locus of ridge subduction during the last 10 Myr (Hampel, 2002; Saillard et al., 2011; Martinod et al., 2016a). Similarly, smaller aseismic ridges such as the Juan Fernández Ridge and the Iquique Ridge subduct beneath the South American continent at 32 and 21^∘ S, respectively. The intercepts between these bathymetric anomalies and the upper plate are thought to influence the characteristics of interplate coupling and seismic rupture (Bilek et al., 2003; Wang and Bilek, 2011; Geersen et al., 2015; Collot et al., 2017) and mark the boundaries between flat and steep subduction segments and changes between subduction erosion and accretion (Jordan et al., 1983; von Huene et al., 1997; Ramos and Folguera, 2009) (Fig. 1).

In addition to bathymetric anomalies, several studies have shown that variations in the volume of sediments in the trench may control the subduction regime from an erosional mode to an accretionary mode (von Huene and Scholl, 1991; Bangs and Cande, 1997). In addition, the volume of sediment in the trench has also been hypothesized to influence the style of interplate seismicity (Lamb and Davis, 2003). At the southern Chilean margin, thick trench-sediment sequences and a steeper subduction angle correlate primarily with subduction accretion, although the area of the intercept of the continental plate with the Chile Rise spreading center locally exhibits the opposite case (von Huene and Scholl, 1991; Bangs and Cande, 1997). Subduction erosion characterizes the region north of the southern volcanic zone from central and northern Chile to southern Peru (33–15^∘ S) due to decreasing sediment supply to the trench, especially within the flat-slab subduction segments (Stern, 1991; von Huene and Scholl, 1991; Bangs and Cande, 1997; Clift and Vannucchi, 2004). Clift and Hartley (2007) and Lohrmann et al. (2003) argued for an alternate style of slow tectonic erosion leading to underplating of subducted material below the base of the crustal forearc, which is synchronous with tectonic erosion beneath the trenchward part of the forearc. For the northern Andes, several authors also classify the subduction zone as an erosional type (Clift and Vannucchi, 2004; Scholl and Huene, 2007; Marcaillou et al., 2016).

2.1.2 Major continental fault systems in the coastal realm

The South American convergent margin comprises several fault systems with different kinematics whose presence is closely linked to oblique subduction and the motion and deformation of forearc slivers. Here we summarize the main structures that affect the Pacific coastal areas. North of the Talara bend (5^∘ S), active thrusting and dextral strike-slip faulting dominate the coastal lowlands of Ecuador (e.g., Mache, Bahía, Jipijapa faults), although normal faulting also occurs at Punta Galera (Cumilínche fault) and the Manta Peninsula (Río Salado fault) (Fig. 1). Farther south, normal faulting is active in the Gulf of Guayaquil (Posorja fault), and dextral strike-slip faulting occurs at the Santa Elena Peninsula (La Cruz fault) (Veloza et al., 2012; Costa et al., 2020). The most prominent dextral fault in this region is the 2000 km long, NE-striking Dolores–Guayaquil megashear (DGM) which starts in the Gulf of Guayaquil and terminates in the Colombian hinterland east of the range-bounding thrust faults of the Colombian Andes (Veloza et al., 2012; Villegas-Lanza et al., 2016; Costa et al., 2020) (Fig. 1). Normal faults have been described along the coast of Peru at the Illescas Peninsula in the north (6^∘ S), within the El Huevo–Lomas fault system in the San Juan de Marcona area (14.5–16^∘ S), and within the Incapuquio fault system farther south (17–18^∘ S) (Veloza et al., 2012; Villegas-Lanza et al., 2016; Costa et al., 2020). The main fault zones of the Chilean convergent margin comprise the Atacama fault system (AFS) in the Coastal Cordillera extending from Iquique to La Serena (29.75^∘ S; Fig. 1) with predominantly north–south-striking normal faults, which result in the relative uplift of their western side (e.g., Mejillones fault, Salar del Carmen fault) (Naranjo, 1987; González and Carrizo, 2003; Cembrano et al., 2007). Coastal fault systems farther south are located in the Altos de Talinay area (30.5^∘ S; Puerto Aldea fault), near Valparaíso (33^∘ S; Quintay and Valparaíso faults), near the Arauco Peninsula (36–39^∘ S; Santa María and Lanalhue faults), and in between these areas (Topocalma, Pichilemu, Carranza, and Pelluhue faults) (Ota et al., 1995; Melnick et al., 2009, 2020; Santibáñez et al., 2019; Maldonado et al., 2021) (Fig. 1). However, there is still limited knowledge regarding Quaternary slip rates and kinematics and, most importantly, the location of active faults along the forearc region of South America (Jara-Muñoz et al., 2018; Melnick et al., 2019).

2.2 Climate and geomorphic setting

2.2.1 Geomorphology

The 8000 km long Andean orogen is a major, hemisphere-scale feature that can be divided into segments with distinctive geomorphic and tectonic characteristics. The principal segments comprise the NNE–SSW-trending Colombian–Ecuadorian segment (12^∘ N–5^∘ S), the NW–SE-oriented Peruvian segment (5–18^∘ S), and the north–south-trending Chilean segment (18–56^∘ S) (Jaillard et al., 2000) (Fig. 1). Two major breaks separate these segments; these are the Huancabamba bend in northern Peru and the Arica bend at the Peru–Chile border. The distance of the trench from the WSAC coastline averages 118 km and ranges between 44 and 217 km. The depth of the trench varies between 2920 and 8177 m (GEBCO Bathymetric Compilation Group, 2020), and the continental shelf has an average width of 28 km (Paris et al., 2016).

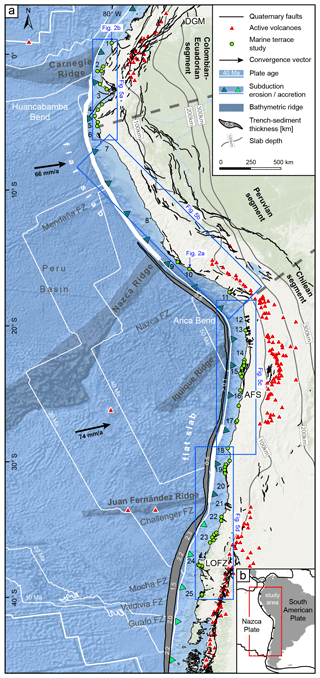
Figure 1 (a) Morphotectonic setting of the South American margin showing major fault systems and crustal faults (Costa et al., 2000; Veloza et al., 2012; Maldonado et al., 2021), slab depth (Hayes et al., 2018), flat-slab subduction segments, active volcanos (Venzke, 2013), bathymetric features of the subducting plate, trench-sediment thickness (Bangs and Cande, 1997), segments of subduction erosion and accretion (Clift and Vannucchi, 2004), plate age (Müller et al., 2008), convergence vectors (DeMets et al., 2010), and marine terrace ages used for lateral correlation. DGM: Dolores–Guayaquil megashear; AFS: Atacama fault system; LOFZ: Liquiñe–Ofqui fault zone; FZ: fracture zone; 1: Punta Galera; 2: Manta Pen.; 3: Gulf of Guayaquil, Santa Elena Pen.; 4: Tablazo Lobitos; 5: Paita Pen.; 6: Illescas Pen.; 7: Chiclayo; 8: Lima; 9: San Juan de Marcona; 10: Chala Bay; 11: Pampa del Palo; 12: Pisagua; 13: Iquique; 14: Tocopilla; 15: Mejillones Pen.; 16: Taltal; 17: Caldera; 18: Punta Choros; 19: Altos de Talinay; 20: Los Vilos; 21: Valparaíso; 22: Topocalma; 23: Carranza; 24: Arauco Pen.; 25: Valdivia (World Ocean Basemap: Esri, Garmin, GEBCO, NOAA NGDC, and other contributors). (b) Location of the study area.

In the 50 to 180 km wide coastal area of the Ecuadorian Andes, where the Western Cordillera is flanked by a structural depression, relief is relatively low (< 300 m a.s.l.). The Gulf of Guayaquil (3^∘ S) and the Dolores–Guayaquil megashear separate the northern from the southern forearc units. The coast-trench distance along the Huancabamba bend is quite small (∼ 55–90 km), except for the Gulf of Guayaquil, and the trench east of the Carnegie Ridge is at a relatively shallow depth of ∼ 3.5 km. Farther south, the Peruvian forearc comprises the up to 160 km wide Coastal Plains in the north and the narrow, 3000 m high Western Cordillera. While the Coastal Plains in north-central Peru are relatively narrow (< 40 km), they widen in southern Peru, and the elevation of the Western Cordillera increases to more than 5000 m (Suárez et al., 1983; Jaillard et al., 2000). The region between the coast and the trench in central Peru (up to 220 km) narrows toward the San Juan de Marcona area (∼ 75 km) near the intercept with the Nazca Ridge, and the relatively deep trench (∼ 6.5 km) becomes shallower (< 5 km) (GEBCO Bathymetric Compilation Group, 2020). Between 18 and 28^∘ S, the Chilean forearc comprises the 50 km wide and up to 2700 m high Coastal Cordillera, which is separated from the Precordillera by the Central Depression. In the flat-slab subduction segment between 27 and 33^∘ S there is neither a morphotectonic region characterized by a central depression nor active volcanism in the high Andean cordillera (Fig. 1) (Jordan et al., 1983). The Chilean forearc comprises the Coastal Cordillera, which varies in altitude from up to 2000 m at 33^∘ S to 500 m at 46^∘ S, and the Central Depression that separates the forearc from the Main Cordillera. From the Arica bend, where the coast-trench distance is up to 170 km and the trench ∼ 8 km deep, a slight increase in coast-trench distance can be observed in Chile toward the south (∼ 80–130 km), as can a decrease in trench depth to ∼ 4.5 km.

2.2.2 Marine terraces and coastal uplift rates

Wave erosion generates wave-cut terrace levels, while the accumulation of shallow marine sediments during sea-level highstands forms wave-built terraces. Another type of terrace is known as “rasa” and refers to wide shore platforms formed under slow-uplift conditions (< 0.2 m kyr⁻¹) and the repeated reoccupation of this surface by high sea levels (Regard et al., 2010; Rodríguez et al., 2013; Melnick, 2016). Other studies indicate a stronger influence of climate and rock resistance to erosion compared to marine wave action (Prémaillon et al., 2018). Typically, the formation of Pleistocene marine terraces in the study area occurred during interglacial and interstadial relative sea-level highstands that were superposed on the uplifting coastal areas; according to the Quaternary oxygen-isotope curve defining warm and cold periods, high Quaternary sea levels have been correlated with warm periods and are denoted with the odd-numbered Marine Isotope Stages (MISs) (Lajoie, 1986; Shackleton et al., 2003).

Along the WSAC, staircase-like sequences of multiple marine terraces are preserved nearly continuously along the coast. These terraces comprise primarily wave-cut surfaces that are frequently covered by beach ridges of siliciclastic sediments and local accumulations of carbonate bioclastic materials (Ota et al., 1995; Saillard et al., 2009; Rodríguez et al., 2013; Martinod et al., 2016b). Rasa surfaces exist in the regions of southern Peru and northern Chile (Regard et al., 2010; Rodríguez et al., 2013; Melnick, 2016). Particularly the well-preserved MIS 5e terrace level has been largely used as a strain marker in the correlation of uplifted coastal sectors due to its lateral continuity and high potential for preservation. Global observations of sea-level fluctuations during MIS 5 allow us to differentiate between three second-order highstands at 80 ka (5a), 105 ka (5c), and 128 to 116 ka (5e) with paleo sea levels of −20 m for both of the younger and $+\mathrm{3}\pm \mathrm{3}$ m for the oldest highstand (Stirling et al., 1998; Siddall et al., 2006; Hearty et al., 2007; Rohling et al., 2009; Pedoja et al., 2011), although glacio-isostatic adjustments (GIAs) can cause local differences of up to 30 m (Simms et al., 2016; Creveling et al., 2017). The database generated in this study is based exclusively on the last interglacial marine terraces exposed along the WSAC between Ecuador and southern Chile (1–40^∘ S). In the following section we present a brief review of previously studied marine terrace sites in this area.

Paleo-shoreline elevations of the last interglacial (MIS 5e) in Ecuador are found at elevations of around 45 ± 2 m a.s.l. in Punta Galera (Esmeraldas area), 43–57 ± 2 m on the Manta Peninsula and La Plata Island, and 15±5 m a.s.l. on the Santa Elena Peninsula (Pedoja et al., 2006b, a). In northern Peru, MIS 5e terraces have been described at elevations of 18–31 m a.s.l. for the Tablazo Lobitos (Cancas and Mancora areas), at 25 ± 5 m a.s.l. on the Paita Peninsula, and at 18 ± 3 m a.s.l. on the Illescas Peninsula and the Bay of Bayovar (Pedoja et al., 2006b). Farther south, MIS 5e terraces are exceptionally high in the San Juan de Marcona area immediately south of the subducting Nazca Ridge, with maximum elevations of 80 m at the Cerro Trés Hermanas and 105 m at the Cerro El Huevo (Hsu et al., 1989; Ortlieb and Macharé, 1990; Saillard et al., 2011). The Pampa del Palo region in southern Peru exhibits relatively thick vertical stacks of shallow marine terrace deposits related to MIS 7, 5e (∼ 20 m), and 5c that may indicate a different geodynamic behavior compared to adjacent regions (Ortlieb et al., 1996b). In central and northern Chile, the terrace levels of the last interglacial occur at 250–400, 150–240, 80–130, and 30–40 m and in southern Chile at 170–200, 70, 20–38, and 8–10 m (Fuenzalida et al., 1965). Specifically, between 24 and 32^∘ S, paleo-shoreline elevations of the last interglacial (MIS 5e) range between 25 and 45 m (Ota et al., 1995; Saillard et al., 2009; Martinod et al., 2016b). Shore platforms are higher in the Altos de Talinay area (30.3–31.3^∘ S) but are small, poorly preserved, and terminate at a high coastal scarp between 26.75 and 24^∘ S (Martinod et al., 2016b). Shoreline-angle elevations between 34 and 38^∘ S (along the Maule seismotectonic segment) vary from high altitudes in the Arauco and Topocalma areas (200 m) to moderate elevations near Carranza (110 m) and to very low elevations in between (15 m) (Melnick et al., 2009; Jara-Muñoz et al., 2015).

Coastal uplift-rate estimates along the WSAC mainly comprise calculations for the Talara Arc, the San Juan de Marcona area, the Mejillones Peninsula, the Altos de Talinay area, and several regions in south-central Chile. Along the Talara Arc (6.5^∘ S–1^∘ N), marine terraces of the Manta Peninsula and La Plata Island in central Ecuador indicate the most pronounced uplift rates of 0.31–0.42 m kyr⁻¹ since MIS 5e, while similar uplift rates are documented to the north in the Esmeraldas area (0.34 m kyr⁻¹) and lower ones to the south at the Santa Elena Peninsula (0.1 m kyr⁻¹). In northern Peru, last interglacial uplift rates are relative low, ranging from 0.17–0.21 m kyr⁻¹ for the Tablazo Lobitos and 0.16 m kyr⁻¹ for the Paita Peninsula to 0.12 m kyr⁻¹ for the Bay of Bayovar and the Illescas Peninsula (Pedoja et al., 2006b, a). Marine terraces on the continental plate above the subducting Nazca Ridge (13.5–15.6^∘ S) record variations in uplift rate where the coastal forearc above the northern flank of the ridge is either stable or has undergone net subsidence (Macharé and Ortlieb, 1992). The coast above the ridge crest has been rising at about 0.3 m kyr⁻¹ and the coast above the southern flank (San Juan de Marcona) has been uplifting at a rate of 0.5 m kyr⁻¹ (Hsu, 1992) or even 0.7 m kyr⁻¹ (Ortlieb and Macharé, 1990) for at least the last 125 kyr. Saillard et al. (2011) state that long-term regional uplift in the San Juan de Marcona area has increased since about 800 ka related to the southward migration of the Nazca Ridge, and it ranges from 0.44 to 0.87 m kyr⁻¹. The Pampa del Palo area in southern Peru rose more slowly or was even down-faulted and had subsided with respect to the adjacent coastal regions (Ortlieb et al., 1996b). These movements ceased after the highstand during the MIS 5e, and slow-uplift rates of approximately 0.16 m kyr⁻¹ have characterized the region since 100 ka (Ortlieb et al., 1996b). In northern Chile (24–32^∘ S), uplift rates for the Late Pleistocene average around 0.28 ± 0.15 m kyr⁻¹ (Martinod et al., 2016b), except for the Altos de Talinay area where pulses of rapid uplift occurred during the Middle Pleistocene (Ota et al., 1995; Saillard et al., 2009; Martinod et al., 2016b). The Central Andean rasa (15–33^∘ S) and Lower to Middle Pleistocene shore platforms – which are also generally wider – indicate a period of tectonic stability or subsidence followed by accelerated and spatially continuous uplift after ∼ 400 ka (MIS 11) (Regard et al., 2010; Rodríguez et al., 2013; Martinod et al., 2016b). However, according to Melnick (2016), the central Andean rasa has experienced slow and steady long-term uplift with a rate of 0.13 ± 0.04 m kyr⁻¹ during the Quaternary, predominantly accumulating strain through deep earthquakes at the crust–mantle boundary (Moho) below the locked portion of the plate interface. The lowest uplift rates occur at the Arica bend and increase gradually southward; the highest values are attained along geomorphically distinct peninsulas (Melnick, 2016). In the Maule segment (34–38^∘ S), the mean uplift rate for the MIS 5 terrace level is 0.5 m kyr⁻¹, exceeded only in the areas of Topocalma, Carranza, and Arauco, where it amounts to 1.6 m kyr⁻¹ (Melnick et al., 2009; Jara-Muñoz et al., 2015). Although there are several studies of marine terraces along the WSAC, these are isolated and based on different methodological approaches, mapping and leveling resolutions, and dating techniques, which make regional comparisons and correlations difficult in the context of the data presented here.

2.2.3 Climate

Apart from latitudinal temperature changes, the present-day morphotectonic provinces along the South American margin have a pronounced impact on the precipitation gradients on the west coast of South America. Since mountain ranges are oriented approximately perpendicular to moisture-bearing winds, they affect both flanks of the orogen (Strecker et al., 2007). The regional-scale pattern of wind circulation is dominated by westerly winds at subtropical and extratropical latitudes primarily up to about 27^∘ S (Garreaud, 2009). However, anticyclones over the South Pacific result in winds blowing from the south along the coast between 35^∘ S and 10^∘ S (Garreaud, 2009). The moisture in the equatorial Andes (Ecuador and Colombia) and in the areas farther south (27^∘ S) is fed by winds from the Amazon basin and the Gulf of Panama, resulting in rainfall mainly on the eastern flanks of the mountain range (Bendix et al., 2006; Bookhagen and Strecker, 2008; Garreaud, 2009). The Andes of southern Ecuador, Peru, and northern Chile are dominated by a rain-shadow effect that causes aridity within the Andean Plateau (Altiplano-Puna), the Western Cordillera, and the coastal region (Houston and Hartley, 2003; Strecker et al., 2007; Garreaud, 2009). Furthermore, the aridity is exacerbated by the effects of the cold Humboldt current which prevents humidity from the Pacific from penetrating inland (Houston and Hartley, 2003; Garreaud, 2009; Coudurier-Curveur et al., 2015). The precipitation gradient reverses between 27 and 35^∘ S where the Southern Hemisphere westerlies cause abundant rainfall on the western flanks of the Coastal and Main cordilleras (Garreaud, 2009). Martinod et al. (2016b) proposed that latitudinal differences in climate largely influence coastal morphology, specifically the formation of high coastal scarps that prevent the development of extensive marine terrace sequences. However, the details of this relationship have not been conclusively studied along the full extent of the Pacific coast of South America.

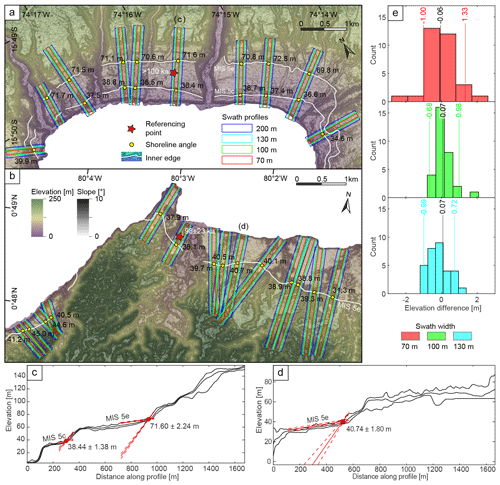
Figure 2 Orthometrically corrected TanDEM-X and slope map of (a) Chala Bay in south-central Peru and (b) Punta Galera in northern Ecuador with mapped inner shoreline edges of the MIS 5e and 5c terrace levels. Colored rectangles represent swath-profile boxes of various widths that were placed perpendicular to the inner edges for the subsequent estimation of terrace elevation in TerraceM. The red star indicates the referencing point with the age constraint for the respective area (Pedoja et al., 2006b; Saillard, 2008). Panels (c) and (d) show the estimation of shoreline-angle elevations in TerraceM by intersecting linear-regression fits of the paleo-cliff and paleo-platform (200 m wide swath profiles). (e) Histograms of elevation differences measured in both areas for various swath widths (70, 100, and 130 m) with respect to the 200 m wide reference swath profile (blue). Vertical lines indicate median values and standard deviations (2σ).

3 Methods

We combined – and describe in detail below – bibliographic information, different topographic data sets, and uniform morphometric and statistical approaches to assess the elevation of marine terraces and accompanying vertical deformation rates along the western South American margin.

3.1 Mapping of marine terraces

Marine terraces are primarily described based on their elevation, which is essential for determining vertical deformation rates. The measurements of the marine terrace elevations of the last interglacial were performed using TanDEM-X topography (12 and 30 m horizontal resolution) (German Aerospace Center, DLR, 2018) and digital terrain models from lidar (1, 2.5, and 5 m horizontal resolution). The digital elevation models (DEMs) were converted to orthometric heights by subtracting the EGM2008 geoid and projected in the universal transverse mercator (UTM) coordinate system using the World Geodetic System (WGS1984) using zone 19S for Chile, zone 18S for southern and central Peru, and zone 17S for northern Peru and Ecuador.

To trace the MIS 5 shoreline, we mapped its inner edge along the west coast of South America based on slope changes in TanDEM-X topography at the foot of paleo-cliffs (Jara-Muñoz et al., 2016) (Fig. 2a and b). To facilitate mapping, we used slope and hillshade maps. We correlated the results of the inner-edge mapping with the marine terraces catalog of Pedoja et al. (2011) and references therein (Sect. 2.2.2, Table 1). Further references used to validate MIS 5e terrace heights include Victor et al. (2011) for the Pampa de Mejillones, Martinod et al. (2016b) for northern Chile, and Jara-Muñoz et al. (2015) for the area between 34 and 38^∘ S. We define the term “referencing point” for these previously published terrace heights and age constraints. The referencing point with the shortest distance to the location of our measurements served as a topographical and chronological benchmark for mapping the MIS 5 terrace in the respective areas. In addition, this distance is used to assign a quality rating (QR) to our measurements.

Table 1 Age constraints used for mapping of the inner edge of MIS 5 and for verifying our terrace-elevation measurements. This compilation is mainly based on the terrace catalog of Pedoja et al. (2011); added references include Victor et al. (2011) for Pampa de Mejillones, Martinod et al. (2016b) for northern Chile, and Jara-Muñoz et al. (2015) for south-central Chile. Absolute ages refer to MIS 5e marine terraces unless otherwise specified; inferred ages refer to their associated MIS. IRSL: infrared-stimulated luminescence, AAR: amino-acid racemization, CRN: cosmogenic radionuclides, ESR: electron spin resonance.

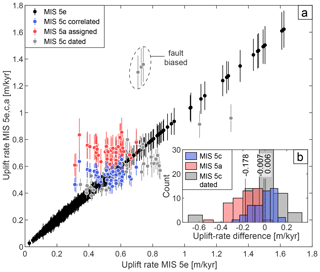
Figure 3 Comparison of MIS 5 uplift-rate estimates. (a) Uplift rates derived by correlating mapped terrace occurrences located immediately below the MIS 5e level to either MIS 5c (blue) or MIS 5a (red) with respect to MIS 5e uplift rates. Marine terraces correlated to MIS 5c by an age constraint are plotted in gray color. (b) Histograms of differences between MIS 5a or MIS 5c uplift rates and MIS 5e uplift rates. Vertical lines show median uplift-rate differences. See Sect. 2.2.2 for relative sea-level elevations of MIS 5a, 5c, and 5e.

In addition to MIS 5e, we also mapped MIS 5c in areas with high uplift rates such as at the Manta Peninsula, San Juan de Marcona, Topocalma, Carranza, and Arauco. Although we observed a terrace level correlated to MIS 5a in the Marcona area, we excluded this level from the database due to its limited preservation at other locations and lack of chronological constraints. Our assignment of mapped terrace levels to MIS 5c is primarily based on age constraints by Saillard et al. (2011) for the Marcona area and Jara-Muñoz et al. (2015) for the area between 34 and 38^∘ S. However, in order to evaluate the possibility that our correlation with MIS 5c is flawed, we estimated uplift rates for the lower terraces by assigning them tentatively to either MIS 5a or MIS 5c. We interpolated the uplift rates derived from the MIS 5e level at the sites of the lower terraces and compared the differences (Fig. 3a). If we infer that uplift rates were constant in time at each site throughout the three MIS 5 substages, the comparison suggests these lower terrace levels correspond to MIS 5c because of the smaller difference in uplift rate rather than to MIS 5a (Fig. 3b).

Table 2 Median values and standard deviations (2σ) representing the indicative meaning along the WSAC. The four sectors were chosen based on their main geomorphic characteristics (see Sect. 4).

A rigorous assessment of marine terrace elevations is crucial for determining accurate vertical deformation rates. Since fluvial degradation and hillslope processes subsequent to the abandonment of marine terraces may alter terrace morphology (Anderson et al., 1999; Jara-Muñoz et al., 2015), direct measurements of terrace elevations at the inner edge (foot of the paleo-cliff) may result in overestimation of the terrace elevations and vertical deformation rates (Jara-Muñoz et al., 2015). To precisely measure the shoreline-angle elevations of the MIS 5 terrace level, we used a profile-based approach in TerraceM, a graphical user interface in MATLAB^® (Jara-Muñoz et al., 2016); http://www.terracem.com/ (last access: 6 May 2021). We placed swath profiles of variable width perpendicular to the previously mapped inner edge, which were used by the TerraceM algorithm to extract maximum elevations to avoid areas of fluvial incision (Fig. 2a and b). For the placement of the swath profiles we tried to capture a local representation of marine terrace topography with a sufficiently long, planar paleo-platform and a sufficiently high paleo-cliff, simultaneously avoiding topographic disturbance, such as colluvial wedges or areas affected by incision. North of Caleta Chañaral (29^∘ S), we used swath profiles of 200 m width, although we occasionally used 100 m wide profiles for narrow terrace remnants. South of 29^∘ S, we used swath widths of 130 and 70 m. The width was chosen based on fluvial drainage densities that are associated with precipitation gradients. Sensitivity tests comparing shoreline-angle measurements from different swath widths in the Chala Bay and at Punta Galera show only minimal vertical deviations of less than 0.5 m (Fig. 2e). The sections of these profiles, which represent the undisturbed paleo-platform and paleo-cliff areas, were picked manually and fitted by linear regression. The extrapolated intersection between both regression lines ultimately allowed us to determine the buried shoreline-angle elevation and associated uncertainty, which is derived from the 95 % confidence interval (2σ) of both regressions (Fig. 2c and d). In total, we measured 1843 MIS 5e and 110 MIS 5c shoreline-angle elevations. To quantify the paleo-position of the relative sea-level elevation and the involved uncertainty for the WALIS database, we calculated the indicative meaning for each marine terrace measurement using the IMCalc software from Lorscheid and Rovere (2019). The indicative meaning comprises the range between the lower and upper limits of sea-level formation – the indicative range – as well as its mathematically averaged position, which corresponds to the reference water level (Lorscheid and Rovere, 2019). Table 2 documents the medians and standard deviations of these values for four extensive regions along the WSAC.

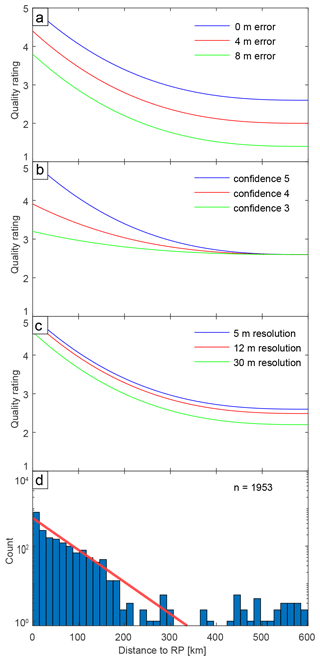
Figure 4 Influence of the parameters on the quality rating. The x axis is the distance to reference point (RP), the y axis is the quality rating, and the color lines represent different values of quality-rating parameters. While one parameter is being tested, the remaining parameters are set to their best values. That is why the QR does not reach values of 1 in the graphs displayed here. (a) Shoreline-angle elevation error. (b) Confidence value of the referencing point. (c) Topographic resolution of the DEM used for terrace-elevation estimation. (d) Histogram displaying the distribution of distances between each shoreline-angle measurement and its nearest RP (n: number of measurements). The red line is an exponential fit.

To quantify the reliability and consistency of our shoreline-angle measurements, we developed a quality rating from low (1) to high (5) confidence. Equation (1) illustrates how we calculated the individual parameters and the overall quality rating:

$$\begin{array}{}\text{(1)}& \begin{array}{rl}\text{QR}=\mathrm{1}& +\mathrm{2.4}\times {\left({\displaystyle \frac{C_{\text{RP}}}{max\left(C_{\text{RP}}\right)}}\times \left(\mathrm{1}-{\displaystyle \frac{D_{\text{RP}}}{max\left(D_{\text{RP}}\right)}}\right)\right)}^e\\ & +\mathrm{1.2}\times \left(\mathrm{1}-{\displaystyle \frac{E_{\text{T}}}{max\left(E_{\text{T}}\right)}}\right)\\ & +\mathrm{0.4}\times \mathrm{1.2}\times \left(\mathrm{1}-{\displaystyle \frac{R}{max\left(R\right)}}\right).\end{array}\end{array}$$

The four parameters included in our quality rating (QR) comprise (a) the distance to the nearest referencing point (D_RP), (b) the confidence of the referencing point based on the dating method used by previous studies (C_RP) (Pedoja et al., 2011), (c) the measurement error in TerraceM (E_T), and (d) the pixel-scale resolution of the topographic data set (R) (Fig. 4). We did not include the error that results from the usage of different swath widths since the calculated elevation difference with respect to the most frequently used 200 m swath width is very low (< 0.5 m) (Fig. 2e). From the reference points we only used data points with a confidence value of 3 or greater (1 – poor, 5 – very good) based on the previous qualification of Pedoja et al. (2011). The confidence depends mainly on the reliability of the dating method but can be increased by good age constraints of adjacent terrace levels or detailed morphostratigraphic correlations, such as in Chala Bay (Fig. 2a) (Goy et al., 1992; Saillard, 2008). We further used this confidence value to quantify the quality of the age constraints in the WALIS template.

To account for the different uncertainties of the individual parameters in the QR, we combined and weighted the parameters D_RP and C_RP in a first equation claiming 60 % of the final QR, E_T in a second, and R in a third equation weighted 30 % and 10 %, respectively. We justify these percentages by the fact that the distance and confidence to the nearest referencing point is of utmost importance for identifying the MIS 5e terrace level. The measurement error represents how well the mapping of the paleo-platform and paleo-cliff resulted in the shoreline-angle measurement, while the topographic resolution of the underlying DEM only influences the precise representation of the actual topography and has little impact on the measurement itself. The coefficient assigned to the topographic resolution is multiplied by a factor of 1.2 in order to maintain the possibility of a maximum QR for a DEM resolution of 5 m. Furthermore, we added an exponent to the first part of the equation to reinforce low confidence and/or high distance of the referencing point for low-quality ratings. The exponent adjusts the QR according to the distribution of distances from referencing points, which follows an exponential relationship (Fig. 4d).

The influence of each parameter to the quality rating can be observed in Fig. 4. We observe that for high D_RP values the QR becomes constant; likewise, the influence of QR parameters becomes significant for QR values higher than 3. We justify the constancy of the QR for high D_RP values (> 300 km) by the fact that most terrace measurements have D_RP values below 200 km (Fig. 4d). The quality rating is then used as a descriptor of the confidence of marine terrace-elevation measurements.

3.2 Estimating coastal uplift rates

Uplift-rate estimates from marine terraces (u) were calculated using Eqs. (2) and (3):

$$\begin{array}{}\text{(2)}& {\displaystyle }& {\displaystyle }\mathrm{\Delta }H=H_{\text{T}}-H_{\text{SL}},\text{(3)}& {\displaystyle }& {\displaystyle }u={\displaystyle \frac{H_{\text{T}}-H_{\text{SL}}}{T}},\end{array}$$

where ΔHis the relative sea level, H_SL is the sea-level altitude of the interglacial maximum, H_T is the shoreline-angle elevation of the marine terrace, and T is its associated age (Lajoie, 1986).

We calculated the standard error SE(u) using Eq. (4) from Gallen et al. (2014):

$$\begin{array}{}\text{(4)}& {\displaystyle }\text{SE}(u{)}^{\mathrm{2}}=u^{\mathrm{2}}\left(\left({\displaystyle \frac{{\mathit{\sigma }}_{\mathrm{\Delta }H}^{\mathrm{2}}}{\mathrm{\Delta }{H}^{\mathrm{2}}}}\right)+\left({\displaystyle \frac{{\mathit{\sigma }}_{\text{T}}^{\mathrm{2}}}{T^{\mathrm{2}}}}\right)\right),\end{array}$$

where ${\mathit{\sigma }}_{\mathrm{\Delta }H}^{\mathrm{2}}$, the error in relative sea level, equals $({\mathit{\sigma }}_{H_{\text{T}}}^{\mathrm{2}}+{\mathit{\sigma }}_{H_{\text{SL}}}^{\mathrm{2}})$. The standard-error estimates comprise the uncertainty in shoreline-angle elevations from TerraceM $\left({\mathit{\sigma }}_{H_{\text{T}}}\right)$, error estimates in absolute sea level $\left({\mathit{\sigma }}_{H_{\text{SL}}}\right)$ from Rohling et al. (2009), and an arbitrary range of 10 kyr for the duration of the highstand (σ_T).

Vertical displacement rates and relative sea level are influenced by flexural rebound associated with loading and unloading of ice sheets during glacio-isostatic adjustments (GIAs) (Stewart et al., 2000; Shepherd and Wingham, 2007). The amplitude and wavelength of GIAs is mostly determined by the flexural rigidity of the lithosphere (Turcotte and Schubert, 1982) and should therefore not severely influence vertical deformation along non-glaciated coastal regions (Rabassa and Clapperton, 1990) that are located in the forearc of active subduction zones. This is supported by Creveling et al. (2017) who showed no significant GIA along the WSAC between 1^∘ N and 40^∘ S since MIS 5a. Current GIA models use an oversimplified lithospheric structure defined by horizontal layers of homogeneous rheology (e.g., Creveling et al., 2017), which might be appropriate for cratons and ocean basins but not necessarily for the forearcs of subduction margins. Therefore, we did not account for the GIA effect on terrace elevations and uplift rates.

3.3 Tectonic parameters of the South American convergent margin

We compared the deformation patterns of marine terraces along the coast of South America with proxies that included crustal faults, bathymetric anomalies, trench-sediment thickness, and distance to the trench. To evaluate the possible control of climatic parameters in the morphology of marine terraces, we compared our data set with wave heights, tidal range, mean annual precipitation rate, and the azimuth of the coastline (Schweller et al., 1981; Bangs and Cande, 1997; von Huene et al., 1997; Collot et al., 2002; Ceccherini et al., 2015; Hayes et al., 2018; Santibáñez et al., 2019; GEBCO Bathymetric Compilation Group, 2020) (Fig. 1).

To evaluate the potential correlations between tectonic parameters and marine terraces, we analyzed the latitudinal variability of these parameters projected along a curved “simple profile” and a 300 km wide “swath profile” following the trace of the trench. We used simple profiles for visualizing 2D data sets; for instance, to compare crustal faults along the forearc area of the margin (Veloza et al., 2012; Maldonado et al., 2021), we projected the seaward tip of each fault. For the trench-sediment thickness, we projected discrete thickness estimates based on measurements from seismic reflection profiles of Bangs and Cande (1997), Collot et al. (2002), Huene et al. (1996), and Schweller et al. (1981). Finally, we projected the discrete trench distances from the point locations of our marine terrace measurements along a simple profile. To compare bathymetric features on the oceanic plate, we used a compilation of bathymetric measurements at 450 m resolution (GEBCO Bathymetric Compilation Group, 2020). The data set was projected along a curved, 300 km wide swath profile using TopoToolbox (Schwanghart and Kuhn, 2010).

Finally, to elucidate the influence of climatic factors on marine terrace morphology, we compared the elevation but also the number of measurements as a proxy for the preservation and exposure of marine terraces. We calculated wave heights, tidal ranges, and reference water levels at the point locations of our marine terrace measurements using the indicative meaning calculator (IMCalc) from Lorscheid and Rovere (2019). We used the maximum values of the hourly significant wave height, and for the tidal range we calculated the difference between the highest and lowest astronomical tide. The reference water level represents the averaged position of the paleo sea level with respect to the shoreline-angle elevation and, together with the indicative range (uncertainty), quantifies the indicative meaning (Lorscheid and Rovere, 2019). We furthermore used the high-resolution data set of Ceccherini et al. (2015) for mean annual precipitation, and we compared the azimuth of the coast in order to evaluate its exposure to wind and waves. To facilitate these comparisons, we extracted the values of all these parameters at the point locations of our marine terrace measurements and projected them along a simple profile. Calculations and outputs were processed and elaborated using MATLAB^® (2020b).

4 Results

4.1 Marine terrace geomorphology and shoreline-angle elevations

In the following sections we describe our synthesized database of last interglacial marine terrace elevations along the WSAC. Marine terraces of the last interglacial are generally well preserved and almost continuously exposed along the WSAC, allowing the estimation of elevations with a high spatial density. To facilitate the descriptions of marine terrace-elevation patterns, we divided the coastline into four sectors based on their main geomorphic characteristics (Fig. 5): (1) the Talara bend in northern Peru and Ecuador, (2) southern and central Peru, (3) northern Chile, and (4) central and south-central Chile. In total we carried out 1843 MIS 5e terrace measurements with a median elevation of 30.1 m a.s.l. and 110 MIS 5c terrace measurements with a median of 38.6 m. The regions with exceptionally high marine terrace elevations (≥ 100 m) comprise the Manta Peninsula in Ecuador, the San Juan de Marcona area in south-central Peru, and three regions in south-central Chile (Topocalma, Carranza, and Arauco). Marine terraces at high altitudes (≥ 60 m) can also be found in Chile on the Mejillones Peninsula, south of Los Vilos, near Valparaíso, in Tirúa, and near Valdivia, while terrace levels only slightly above the median elevation are located at Punta Galera in Ecuador, south of Puerto Flamenco, at Caldera and Bahía Inglesa, near Caleta Chañaral, and near the Quebrada El Moray in the Altos de Talinay area in Chile. In the following sections we describe the characteristics of each site in detail; the names of the sites are written in brackets following the same nomenclature as in the WALIS database (i.e., Pe – Peru, Ec – Ecuador, Ch – Chile).

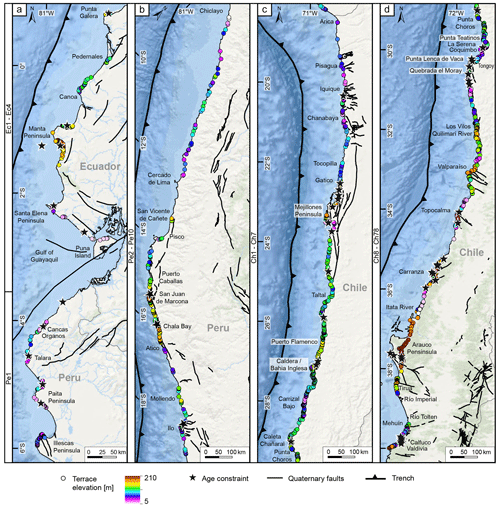
Figure 5 Shoreline-angle elevation measurements (colored points), referencing points (black stars), Quaternary faults (bold black lines) (Veloza et al., 2012; Maldonado et al., 2021), and locations mentioned in the text for the four main geomorphic segments (for location see Fig. 1a) (World Ocean Basemap: Esri, Garmin, GEBCO, NOAA NGDC, and other contributors). Site names referring to the entries in the WALIS database are on the left margin of each panel (Pe – Peru, Ec – Ecuador, Ch – Chile). (a) Talara bend in Ecuador and northern Peru. (b) Central and southern Peru. (c) Northern Chile. (d) Central and south-central Chile.

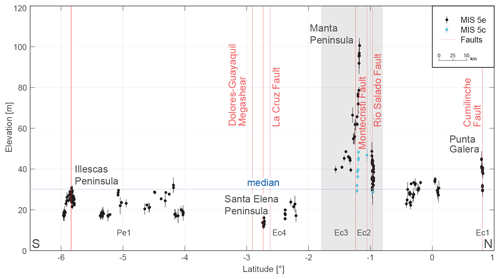
Figure 6 Measured shoreline-angle elevations of MIS 5e and 5c in Ecuador (Ec) and northern Peru (Pe). A high and inferred long-wavelength change in terrace elevation occurs at the Manta Peninsula (gray area) and at low elevations farther south at the Santa Elena Peninsula. Several terrace-elevation changes over short distances coincide with faulting at Punta Galera and on the Illescas Peninsula. Median elevation: 30.1 m. For location see Fig. 5a.

4.1.1 Ecuador and northern Peru (1^∘ N–6.5^∘ S)

The MIS 5e terrace levels in Ecuador and northern Peru (sites Ec1 to Ec4 and Pe1) are discontinuously preserved along the coast (Fig. 6). They often occur at low elevations (between 12 and 30 m) and show abrupt local changes in elevation, reaching a maximum at the Manta Peninsula. Punta Galera in northern Ecuador displays relatively broad and well-preserved marine terraces ranging between 40 and 45 m elevation that rapidly decrease eastward to about 30 m a.s.l. across the Cumilínche fault (Ec1). Farther south, between Pedernales and Canoa (Ec1), narrow terraces occur at lower altitudes of 22–34 m a.s.l. A long-wavelength (∼ 120 km) pattern in terrace-elevation change can be observed across the Manta Peninsula with the highest MIS 5e terraces peaking at ∼ 100 m a.s.l. at its southern coast (Ec2). This terrace level is hardly visible in its highest areas with platform widths smaller than 100 m due to deeply incised and narrowly spaced river valleys. We observe lower and variable elevations between 30 and 50 m across the Rio Salado fault in the San Mateo paleo-gulf in the north, while the terrace elevations increase gradually from ∼ 40 m in the Pile paleo-gulf in the south (Ec3) toward the center of the peninsula (El Aromo dome) and the Montecristi fault (Ec3). A lower terrace level correlated to MIS 5c displays similar elevation patterns as MIS 5e within the Pile paleo-gulf and areas to the north. Near the Gulf of Guayaquil and the Dolores–Guayaquil megashear, the lowest terrace elevations occur at the Santa Elena Peninsula ranging between 17 and 24 m a.s.l., even lower altitudes in its southern part, and between 11 and 16 m a.s.l. on the Puna Island (Ec4). In northern Peru (Pe1), we observe dismembered MIS 5e terraces in the coastal area between Cancas and Talara below the prominent Mancora Tablazo. “Tablazo” is a local descriptive name used in northern Peru (∼ 3.5–6.5^∘ S) for marine terraces that cover a particularly wide surface area (Pedoja et al., 2006b). South of Cancas, MIS 5e terrace elevations range between 17 and 20 m a.s.l., reaching 32 m near Organos, and vary between 20 and 29 m in the vicinity of Talara. In the southward continuation of the Talara harbor, the Talara Tablazo widens, with a lower marine terrace at about 23 m a.s.l. immediately north of Paita Peninsula reaching 30 m a.s.l. in the northern part of the peninsula. The last occurrence of well-preserved MIS 5e terraces in this sector exists at the Illescas Peninsula, where terrace elevations decrease from around 30 to 17 m a.s.l. southward.

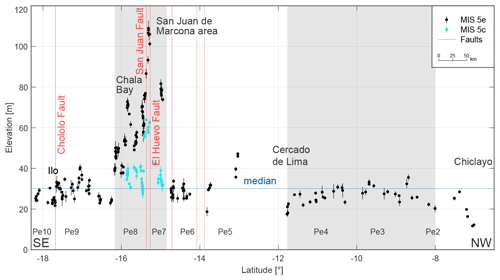
Figure 7 Measured shoreline-angle elevations of MIS 5e and 5c terraces in central and southern Peru (Pe). While only sparsely preserved terraces below the median (30.1 m) occur in central Peru between Chiclayo and Lima, a relatively broad and asymmetric distribution of marine terraces characterizes the area of San Juan de Marcona. For location see Fig. 5b.

4.1.2 Central and southern Peru (6.5–18.3^∘ S)

This segment comprises marine terraces at relatively low and constant elevations but which are rather discontinuous (sites Pe2 to Pe10), except in the San Juan de Marcona area where the terraces increase in elevation drastically (Fig. 7). The coast in north-central Peru exhibits poor records of MIS 5e marine terraces characterized by mostly narrow and discontinuous remnants that are sparsely distributed along the margin with limited age constraints. Marine terraces increase in elevation from 11 to 35 m a.s.l. south of Chiclayo (Pe2) and decrease to 17 m a.s.l. near Cercado de Lima (Pe3, Pe4), forming a long-wavelength (∼ 600 km), small amplitude (∼ 20 m) upwarped structure. The MIS 5e terrace levels are better expressed in the south-central and southern part of Peru at elevations between 35 and 47 m a.s.l. in San Vicente de Cañete, decreasing to approximately 30 m a.s.l. in the vicinity of Pisco (Pe5). South of Pisco, the coastal area becomes narrow with terrace elevations ranging between 25 and 34 m a.s.l. (Pe6) and increasing abruptly to 74–79 m near Puerto Caballas and the Río Grande delta. MIS 5e terrace elevations are highest within the San Juan de Marcona area, reaching 93–109 m at Cerro Huevo and 56–87 m at Cerro Trés Hermanas (Pe7). These higher terrace elevations coincide with a wider coastal area, a better-preserved terrace sequence, and several crustal faults, such as the San Juan and El Huevo faults.

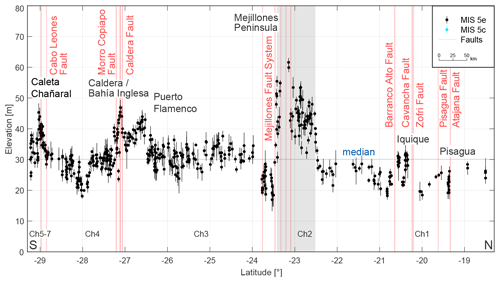
Figure 8 Measured shoreline-angle elevations of MIS 5e and 5c terraces in northern Chile (Ch). Faults and asymmetrically uplifted marine terraces of up to 60 m elevation characterize the Mejillones Peninsula, reaching values below 20 m at the southern margin. Terrace elevations attain peak values south of Puerto Flamenco, at Caldera and Bahía Inglesa, and north of Caleta Chañaral, while in between minimum elevations below 20 m prevail (north of Carrizal Bajo). Median elevation: 30.1 m. For location see Fig. 5c.

Terrace heights west of Yauca indicate a further decrease to 50–58 m before a renewed increase to 70–72 m can be observed in the Chala embayment (Pe8). We observe a similar trend in elevation changes for the shoreline angles attributed to the MIS 5c interglacial within the previously described high-elevation area: 31–39 m near the Río Grande delta, 58–62 m below the Cerro Huevo peak, 27–64 m below the Cerro Trés Hermanas peak (Pe7), 36–40 m near Yauca, and 34–40 m within the Chala embayment (Pe8). Besides various changes in between, terrace elevations decrease slowly from 54 m south of the Chala region to 38 m near Atico (Pe8). The overall decrease south of the San Juan de Marcona area therefore contrasts strikingly with the sharper decrease to the north. These high-elevation marine terraces, which extend ∼ 250 km along the coast from north of the San Juan de Marcona area to south of Chala Bay, constitute one of the longest wavelength structures of the WSAC. SE of Atico, less well-preserved marine terraces appear again in the form of small remnants in a narrower coastal area. Starting with elevations as low as 24 m, MIS 5e terrace altitudes increase southeastward to up to 40 m near Mollendo (Pe9) before they slightly decrease again. The broader and quite well-preserved terraces of the adjacent Ilo area resulted in a smooth increase from values greater than 25 to 33 m and a sudden decrease to as low as 22 m across the Chololo fault (Pe9). North of the Arica bend, shoreline-angle measurements yielded estimates of 24–29 m in altitude (Pe10).

4.1.3 Northern Chile (18.3–29.3^∘ S)

Along the northern Chilean coast, marine terraces of the MIS 5e are characterized by a variable elevation pattern and the occurrence of numerous crustal faults associated with the Atacama fault system, although the changes in terrace elevation are not as pronounced as in the northern segments (Fig. 8) (sites Ch1 to Ch7). The local widening of the coastal area near the Arica bend narrows southward with MIS 5e terraces at elevations of between 24 and 28 m a.s.l. in northernmost Chile (Ch1). Just north of Pisagua, we measured shoreline-angle elevations of well-preserved marine terraces between 19 and 26 m across the Atajana fault (Ch1). An areally limited zigzag pattern starting with shoreline-angle elevation values of 32 m south of Iquique and south of the Zofri and Cavancha faults decreases rapidly to approximately 22 m but increases again to similar altitudes and drops as low as 18 m toward Chanabaya south of the Barranco Alto fault (Ch1). A gentle, steady rise in terrace elevations can be observed south of Tocopilla where altitudes of 25 m are attained. South of Gatico, terrace markers of the MIS 5e highstand increase and continue northward for much of the Mejillones Peninsula within an approximate elevation range of 32–50 m a.s.l. before reaching a maximum of 62 m a.s.l. at the Pampa de Mejillones (Ch2). With its ∼ 100 km latitudinal extent, we consider this terrace-elevation change to be a medium-wavelength structure. Although no MIS 5e terrace levels have been preserved at the Morro Mejillones Horst (Binnie et al., 2016), we measured shoreline-angle elevations at the elevated SW part of the peninsula that decrease sharply from 55 to 17 m a.s.l. in the vicinity of the Mejillones fault system (Ch2). After a short interruption of the MIS 5e terrace level at Pampa Aeropuerto, elevations remain relatively low between 19 and 25 m farther south (Ch2). Along the ∼ 300 km coastal stretch south of Mejillones, marine terraces are scattered along the narrow coastal area ranging between 25 and 37 m a.s.l. (Ch3). South of Puerto Flamenco, MIS 5e terrace elevations range between 40 and 45 m a.s.l. until Caldera and Bahía Inglesa (Ch4). The MIS 5e marine terrace elevations decrease abruptly south of the Caldera fault and the Morro Copiapó (Morro Copiapó fault) to between 25 and 33 m a.s.l., reaching 20 m a.s.l. north of Carrizal Bajo (Ch4). In the southernmost part of the northern Chilean sector, the MIS 5e terraces rise from around 30 m a.s.l. to a maximum of 45 m a.s.l. near the Cabo Leones fault (Ch4) before decreasing in elevation abruptly near Caleta Chañaral and Punta Choros (Ch5, Ch6, Ch7).

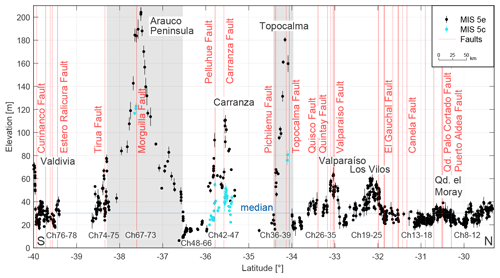
Figure 9 Measured shoreline-angle elevations of MIS 5e and 5c terraces in central Chile (Ch). Extensive faulting coincides with various high terrace elevations of the last interglacial highstand north of Los Vilos, near Valparaíso, at Topocalma, Carranza, and near Valdivia. The most pronounced long-wavelength change in terrace elevation occurs on the Arauco Peninsula with maximum elevations over 200 m and minimum elevations below 10 m north of Concepción. Qd. – Quebrada. Median elevation: 30.1 m. For location see Fig. 5d.

4.1.4 Central Chile (29.3–40^∘ S)

Marine terraces along central Chile display variable, high-amplitude terrace-elevation patterns associated with numerous crustal faults and include a broad-scale change in terrace altitudes with the highest MIS 5e marine terrace elevations of the entire South American margin on the Arauco Peninsula (Fig. 9) (sites Ch8 to Ch78). South of Punta Choros, marine terrace elevations decrease from values close to 40 to 22 m a.s.l. north of Punta Teatinos (Ch8, Ch9). A maximum elevation of 40 m is reached by the terraces just south of this area (Ch10), whereas north of La Serena, a sharp decrease leads to values between 20 and 30 m for marine terraces south of Coquimbo Bay and in the Tongoy Bay area (Ch11, Ch12). South of Punta Lengua de Vaca, our measurements of the exceptionally well-preserved staircase morphology of the terraces are within the same elevation range between 20 and 30 m, increasing slowly to 40 m near the Quebrada el Moray (Ch13). Although we could not observe a significant change in terrace elevation across the Puerto Aldea fault, we measured an offset of ∼ 7 m across the Quebrada Palo Cortado fault. MIS 5e terrace levels decrease thereafter and vary between 20 and 30 m in altitude until north of Los Vilos (Ch14–Ch18) where they increase in elevation (Ch19), reaching 60 m near the Quilimari River (Ch20). The marine terraces become wider in this area and are associated with scattered sea stacks. Decreasing farther south to only 20 m a.s.l. (Ch21–Ch25), the coastal area narrows and has terrace heights of up to 64 m near Valparaíso in an area that is cut by numerous faults (e.g., Valparaíso and Quintay faults) (Ch26–Ch32). Another low-elevation area follows southward, with values as low as 17 m (Ch33–Ch35). Farther south, between 34 and 38^∘ S, broad (∼ 200 km at Arauco), medium (∼ 45 km at Topocalma), and narrow (Carranza) upwarped zones occur that are manifested by variable terrace elevations. These include prominent high-terrace elevations at Topocalma with a maximum of 180 m (Ch36–Ch39), slightly lower levels of 110 m at Carranza (Ch42–Ch47), exceptionally low values near the Itata River (< 10 m) (Ch48–Ch64, Ch66), and the most extensive and highest shoreline-angle elevations on the Arauco Peninsula with elevations in excess of 200 m (Ch67–Ch73). Additionally, we measured MIS 5c terrace elevations in the three higher exposed areas with a range of 20–55 m at Carranza and a few locations at Topocalma (76–81 m) and Arauco (117–123 m). The medium-wavelength structure of Topocalma is bounded by the Pichilemu and Topocalma faults, and near Carranza several fault offsets (e.g., Pelluhue and Carranza faults) are responsible for the short-wavelength changes in terrace elevation. In contrast, crustal faulting is nearly absent in the high-elevation and long-wavelength structure at Arauco. MIS 5e terrace elevations are highly variable within a small area south of the Arauco Peninsula near the Tirúa fault, increasing rapidly from 27 to 78 m and decreasing thereafter to approximately 20 m (Ch74, Ch75). The continuity of terraces is interrupted by the absence of terrace levels between Imperial River and Toltén River but resumes afterward with a highly frequent zigzag pattern and multiple faults (e.g., Estero Ralicura and Curinanco faults) from as low as 18 m to a maximum of 40 m (Ch76, Ch77). In this area locations with the highest terrace levels comprise the terraces near Mehuín and Calfuco. A final increase in shoreline-angle elevations from about 20–30 m up to 76 m near Valdivia coincides with the southern terminus of our terrace-elevation measurements (Ch78).

4.2 Statistical analysis

Our statistical analysis of mapped shoreline-angle elevations resulted in a maximum kernel density at 28.96 m with a 95 % confidence interval from 18.59 to 67.85 m (2σ) for the MIS 5e terrace level (Fig. 10a). The MIS 5c terrace yielded a maximum kernel density at a higher elevation of 37.20 m with 2σ ranging from 24.50 to 63.92 m. It is important to note that the number of MIS 5c measurements is neither as high nor as continuous compared to that of the MIS 5e level. MIS 5c data points were measured almost exclusively at sites where MIS 5e reaches high elevations (e.g., San Juan de Marcona with MIS 5e elevations between 40 and 110 m).

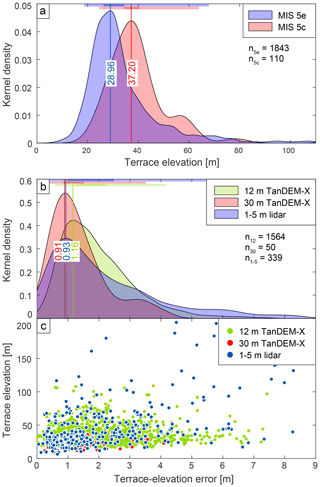
Figure 10 Statistical analysis of measured shoreline-angle elevations. (a) Kernel-density plot of MIS 5e and 5c terrace elevations with maximum likelihood probabilities (MLPs) at 28.96 m elevation for MIS 5e and 37.20 m elevation for MIS 5c (n: number of measurements). Colored bars on top highlight the standard deviations σ and 2σ. (b) Kernel densities and their associated standard-deviation (σ and 2σ) calculations of terrace-elevation errors for source DEMs of various resolutions. The measurements on the most abundant DEM, the 12 m TanDEM-X, have an MLP error of 1.16 m, while the 30 m TanDEM-X and the 1–5 m lidar produce slightly lower errors of 0.91 and 0.93 m, respectively. (c) Terrace-elevation errors plotted against terrace elevation for the individual source DEMs. Although the point density for high terrace elevations is low, a weak correlation of high errors with high terrace elevations can be observed.

The distribution of measurement errors was studied using probability kernel-density plots for each topographic resolution (1–5 m lidar, 12 m TanDEM-X, and 30 m TanDEM-X). The three data sets display similar distributions and maximum likelihood probabilities (MLPs); for instance, lidar data show an MLP of 0.93 m, the 12 m TanDEM-X an MLP of 1.16 m, and 30 m TanDEM-X an MLP of 0.91 m (Fig. 10b). We observe the lowest errors from the 30 m TanDEM-X, slightly higher errors from the 1–5 m lidar data, and the highest errors from the 12 m TanDEM-X. This observation is counterintuitive as we would expect lower errors for topographic data sets with higher resolution (1–5 m lidar). The reason for these errors is probably related to the higher number of measurements using the 12 m TanDEM-X (1564) in comparison with the measurements using 30 m TanDEM-X (50), which result in a higher dispersion and a more realistic representation of the measurement errors (Fig. 10b). In addition, the relation between terrace elevations and error estimates shows that comparatively higher errors are associated with higher terrace elevations, although the sparse point density of high terrace-elevation measurements prevents the recognition of a clear correlation (Fig. 10c).

4.3 Coastal uplift-rate estimates

We calculated uplift rates from 1953 terrace-elevation measurements of MIS 5e (1843) and MIS 5c (110) along the WSAC with a median uplift rate of approximately 0.22 m kyr⁻¹ (Fig. 11). As with the distribution of terrace elevations, we similarly observed several small-scale and large-scale high-amplitude changes in uplift rate along the coast. The most pronounced long-wavelength highs (≥ 1^∘ latitude) in uplift rate are located on the Manta Peninsula (0.79 m kyr⁻¹), in the San Juan de Marcona area (0.85 m kyr⁻¹), and on the Arauco Peninsula (1.62 m kyr⁻¹). Medium-wavelength structures include the Mejillones Peninsula (0.47 m kyr⁻¹) and Topocalma (1.43 m kyr⁻¹), while shorter wavelength structures that are characterized by exceptionally high uplift rates seem to be limited to the central Chilean part of the coastline, especially between 31.5 and 40^∘ S. The most striking example includes Carranza with an uplift rate of up to 0.87 m kyr⁻¹ since the formation of the oldest MIS 5 terrace levels. Lower, but still quite high, uplift rates were calculated for areas north of Los Vilos (0.46 m kyr⁻¹), near Valparaíso (0.49 m kyr⁻¹), and near Valdivia (0.59 m kyr⁻¹). The lowest uplift rates along the South American margin occur at Penco immediately north of Concepción (0.03 m kyr⁻¹), south of Chiclayo in northern Peru (0.07 m kyr⁻¹), and on the southern Santa Elena Peninsula in Ecuador (0.07 m kyr⁻¹).

5 Discussion

5.1 Advantages and limitations of the database of last interglacial marine terrace elevations along the WSAC

In this study we generated a systematic database of last interglacial marine terrace elevations with unprecedented resolution based on an almost continuous mapping of ∼ 2000 measurements along 5000 km of the WSAC. This opens up several possibilities for future applications in which this database can be used; for example, marine terraces are excellent strain markers that can be used in studies on deformation processes at regional scale, and thus the synthesis allows for comparisons between deformation rates at different temporal scales in different sectors of the margin or analyses linking specific climate-driven and tectonic coastal processes and landscape evolution. However, there are a number of limitations and potential uncertainties that can limit the use of this database in such studies without taking several caveats into consideration.

One of the most critical limitations of using the database is associated with the referencing points used to tie our marine terrace measurements which are in turn based on the results and chronological constraints provided by previous studies. The referencing points are heterogeneously distributed along the WSAC, resulting in some cases with distances of up to 600 km to the nearest constrained point, such as in Central Peru, e.g., Pe2. This may have a strong influence on the confidence in the measurement of the marine terrace elevation at these sites. In addition, the geochronological control of some of the referencing points may be based on dating methods with pronounced uncertainties (e.g., amino acid racemization, electron spin resonance, terrestrial cosmogenic radionuclides) which may result in equivocal interpretations and chronologies of marine terrace levels. In order to address these potential factors of uncertainty we defined a quality rating (see Sect. 3.1) which allows us to classify our mapping results based on their confidence and reliability. Therefore, by considering measurements above a defined quality it is possible to increase the level of confidence for future studies using this database; however, this might result in a decrease in the number of measurements available for analysis and comparison.

5.2 Tectonic and climatic controls on the elevation and morphology of marine terraces along the WSAC

In this section we provide a brief synthesis of our data set and its implications for coastal processes and overall landscape evolution influenced by a combination of tectonic and climatic forcing factors. This synthesis emphasizes the significance of our comprehensive data set for a variety of coastal research problems that were briefly introduced in Sect. 5.1. Our detailed measurements of marine terraces along the WSAC reveal variable elevations and a heterogeneous distribution of uplift rates associated with patterns of short, medium, and long wavelengths. In addition, we observe different degrees of development of marine terraces along the margin expressed in variable shoreline-angle densities. There are several possible causes for this variability which we explore by comparing terrace-elevation patterns with different climatic and tectonic parameters.

5.2.1 Tectonic controls on coastal uplift rates

The spatial distribution of the MIS 5 marine terrace elevations along the convergent South American margin has revealed several high-amplitude and long-wavelength changes with respect to tectonically controlled topography. Long-wavelength patterns in terrace elevation (∼ 10² km) are observed at the Manta Peninsula in Ecuador, central Peru between Chiclayo and Lima, San Juan de Marcona (Peru), and on the Arauco Peninsula in Chile, while medium-wavelength structures occur at Mejillones Peninsula and Topocalma (Chile). Instead, short-wavelength patterns in MIS 5 terrace elevations are observed, for instance, near Los Vilos, Valparaíso, and Carranza in Chile.

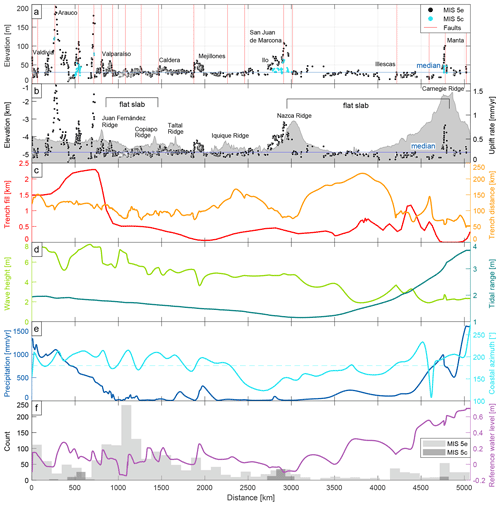
Figure 11 Terrace-elevation and uplift-rate estimates plotted in comparison with various parameters (i.e., bathymetry, trench fill, trench distance, wave height, tidal range, precipitation, and coastal azimuth) that might influence the disparate characteristics of the marine terrace distribution revealed by our data set. We projected these parameters, elevations, and uplift rates with respect to a south–north-oriented polyline that represents the trench. (a) Terrace-elevation measurements and the most important crustal faults (Veloza et al., 2012; Maldonado et al., 2021). This shows the range of altitudes in different regions along the coast and possible relationships between terrace elevation and crustal faulting. The blue horizontal line indicates the median elevation (30.1 m). (b) Coastal uplift rates and mean bathymetry (GEBCO Bathymetric Compilation Group, 2020) of a 150 km swath west of the trench. The blue horizontal line indicates the median uplift rate (0.22 mm yr⁻¹). (c) Sediment thickness of trench-fill deposits (red) (Bangs and Cande, 1997) and the distance of the trench from our terrace measurements (orange). Flat-slab segments of the subducting Nazca plate are indicated for central Chile and Peru. (d) Maximum wave heights along the WSAC (light green) and the tidal range (dark green) between highest and lowest astronomical tides (Lorscheid and Rovere, 2019). (e) Precipitation (blue) along the WSAC (Ceccherini et al., 2015) and azimuthal orientation of the coastline (cyan). (f) Histogram of terrace-elevation measurements along the WSAC.

The subduction of bathymetric anomalies has been shown to exert a substantial influence on upper-plate deformation (Fryer and Smoot, 1985; Taylor et al., 1987; Macharé and Ortlieb, 1992; Cloos and Shreve, 1996; Gardner et al., 2013; Wang and Bilek, 2014; Ruh et al., 2016), resulting in temporally and spatially variable fault activity, kinematics, and deformation rates (Mann et al., 1998; Saillard et al., 2011; Morgan and Bangs, 2017; Melnick et al., 2019). When comparing the uplift pattern of MIS 5 marine terraces and the bathymetry of the oceanic plate, we observe that the two long-wavelength structures in this area, on the Manta Peninsula and at San Juan de Marcona, both coincide with the location of the subducting Nazca and Carnegie ridges, respectively (Fig. 11a and b); this was also previously observed by other authors (Macharé and Ortlieb, 1992; Gutscher et al., 1999; Pedoja et al., 2006a; Saillard et al., 2011). In summary, long-wavelength structures in coastal areas of the upper plate may be associated with deep-seated processes (Melosh and Raefsky, 1980; Watts and Daly, 1981) possibly related to changes in the mechanical behavior of the plate interface. In this context it is interesting that the high uplift rates on the Arauco Peninsula do not correlate with bathymetric anomalies, which may suggest a different deformation mechanism. The scarcity of crustal faults described in the Arauco area rather suggests that shallow structures associated with crustal bending and splay faults occasionally breaching through the upper crust (Melnick et al., 2012; Jara-Muñoz et al., 2015; Jara-Muñoz et al., 2017; Melnick et al., 2019) may cause long-wavelength warping and uplift there (Fig. 11a).

In contrast, small-scale bathymetric anomalies correlate in part with the presence of crustal faults perpendicular to the coastal margin near, for instance, the Juan Fernandez, Taltal, and Copiapó ridges (Fig. 11b); this results in short-wavelength structures and a more localized altitudinal differentiation of uplifted terraces. This emphasizes also the importance of last interglacial marine terraces as strain markers with respect to currently active faults, which might be compared in the future with short-term deformation estimates from GPS or the earthquake catalog. In summary, short-wavelength structures in the coastal realms of western South America may be associated with faults that root at shallow depths within the continental crust (Jara-Muñoz et al., 2015, 2017; Melnick et al., 2019).

The thickness of sediment in the trench is an additional controlling factor on forearc architecture that may determine which areas of the continental margin are subjected to subduction erosion or accretion (Hilde, 1983; Cloos and Shreve, 1988; Menant et al., 2020). Our data show that the accretionary part of the WSAC (south of the intersection with the Juan Fernandez Ridge at 32.9^∘ S) displays faster median uplift rates of 0.26 m kyr⁻¹ than in the rest of the WSAC (Fig. 11b and c). However, no clear correlation is observed between trench fill, uplift rates, and the different structural patterns in the erosive part of the margin. On the other hand, we observe lower uplift rates for greater distances from the trench at the Arica bend, in central Peru, and in the Gulf of Guayaquil, while higher uplift rates occur in areas closer to the trench, such as near the Nazca and Carnegie ridges and the Mejillones Peninsula.

5.2.2 Climatic controls on the formation and preservation of last interglacial marine terraces

The latitudinal climate differences that characterize the western margin of South America may also control coastal morphology and the generation and preservation of marine terraces (Martinod et al., 2016b). In order to evaluate the influence of climate in the generation and/or degradation of marine terraces, we compared the number of marine terrace measurements, which is a proxy for the degree of marine terrace preservation, and climatically controlled parameters such as wave height, tidal range, coastline orientation, and the amount of precipitation.

The maximum wave height along the WSAC decreases northward from ∼ 8 to ∼ 2 m (see Sect. 3.3, Fig. 11d). Similarly, the tidal range decreases progressively northward from 2 to 1 m between Valdivia and San Juan de Marcona, followed by a rapid increase to 4 m between San Juan de Marcona and the Manta Peninsula. We observe an apparent correlation between the number of measurements and the tidal range in the north, between Illescas and Manta (Fig. 11f). Likewise, the increasing trend in the number of measurements southward matches with the increase in wave height (Fig. 11d). An increase in wave height and tidal range may lead to enhanced erosion and morphologically well-expressed marine terraces (Anderson et al., 1999; Trenhaile, 2002), which is consequently reflected in a higher number of measurements that can be carried out. Furthermore, we observe low values for the reference water level (< 0.7 m) resulting from tide and wave-height estimations in IMCalc (Lorscheid and Rovere, 2019), which are used to correct our shoreline-angle measurements in the WALIS database (see Sect. 3.3).

The control of wave-erosion processes on the morphological expression of marine terraces may be counteracted by erosional processes such as river incision. We note that the high number of preserved marine terraces between Mejillones and Valparaíso decreases southward, which coincides with a sharp increase in mean annual precipitation from 10 to 1000 mm yr⁻¹ (Fig. 11e and f) and fluvial dissection. However, in the area with a high number of measurements between the Illescas Peninsula and Manta we observe an opposite correlation: higher rainfall associated with an increase in marine terrace preservation (Fig. 11e). This suggests that the interplay between marine terrace generation and degradation processes apparently buffer each other resulting in different responses under different climatic conditions and coastal settings.

The greater number of marine terraces between Mejillones and Valparaíso and north of Illescas corresponds with a SSW–NNE orientation of the coastline (azimuth between 200 and 220^∘). In contrast, NW–SE- to north–south-oriented coastlines (azimuth between 125 and 180^∘), such as between the Arica and Huancabamba bends, correlate with a lower number of marine terrace measurements (Fig. 11e and f). This observation appears, however, implausible considering that NW–SE-oriented coastlines may be exposed more directly to the erosive effect of storm waves associated with winds approaching from the south. We interpret the orientation of the coastline therefore to be of secondary importance at regional scale for the formation of marine terraces compared to other parameters, such as wave height, tidal range, or rainfall.

6 Conclusions

We measured 1953 shoreline-angle elevations as proxies for paleo sea levels of the MIS 5e and 5c terraces along ∼ 5000 km of the WSAC between Ecuador and southern Chile. Our measurements are based on a systematic methodology, and the resulting data have been standardized within the framework of the WALIS database. Our mapping was tied using referencing points based on previously published terrace-elevation estimates and age constraints that are summarized in the compilation of Pedoja et al. (2011). The limitations of this database are associated with the temporal accuracy and spatial distribution of the referencing points, which we attempt to consider by providing a quality-rating value to each measurement. The marine terrace elevations display a median value of 30.1 m for the MIS 5e level and a median uplift rate of 0.22 m kyr⁻¹ for MIS 5e and 5c. The lowest terrace elevations and uplift rates along the entire WSAC occur immediately north of Concepción in Chile (6 m, 0.03 m kyr⁻¹), south of Chiclayo in northern Peru, and on the Santa Elena Peninsula in Ecuador (both 12 m, 0.07 m kyr⁻¹). The regions with exceptionally high marine terrace elevations (≥ 100 m) comprise the Manta Peninsula in Ecuador, the San Juan de Marcona area in south-central Peru, and three regions in south-central Chile (Topocalma, Carranza, and Arauco).

The pattern of terrace elevations displays short-, medium-, and long-wavelength structures controlled by a combination of various mechanisms. Long-wavelength structures may be controlled by deep-seated processes at the plate interface, such as the subduction of major bathymetric anomalies (e.g., Manta Peninsula and San Juan de Marcona region). In contrast, short- and medium-wavelength deformation patterns may be controlled by crustal faults rooted within the upper plate (e.g., between Mejillones and Valparaíso).

Latitudinal climate characteristics along the WSAC may influence the generation and preservation of marine terraces. An increase in wave height and tidal range generally results in enhanced erosion and morphologically well-expressed, sharply defined marine terraces, which correlates with the southward increase in the number of our marine terrace measurements. Conversely, river incision and lateral scouring in areas with high precipitation may degrade marine terraces, thus decreasing the number of potential marine terrace measurements, such as observed south of Valparaíso.

7 Data availability

The South American database of last interglacial shoreline-angle elevations is available online at https://doi.org/10.5281/zenodo.4309748 (Freisleben et al., 2020). The description of the WALIS-database fields can be found at https://doi.org/10.5281/zenodo.3961543 (Rovere et al., 2020).