the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Global CO2 uptake by cement from 1930 to 2019
Jiaoyue Wang
Longfei Bing
Dan Tong
Philippe Ciais
Steven J. Davis
Robbie M. Andrew
Fengming Xi
Because of the alkaline nature and high calcium content of cements in general, they serve as a CO2-absorbing agent through carbonation processes, resembling silicate weathering in nature. This carbon uptake capacity of cements could abate some of the CO2 emitted during their production. Given the scale of cement production worldwide (4.10 Gt in 2019), a life-cycle assessment is necessary to determine the actual net carbon impacts of this industry. We adopted a comprehensive analytical model to estimate the amount of CO2 that had been absorbed from 1930 to 2019 in four types of cement materials, including concrete, mortar, construction waste, and cement kiln dust (CKD). In addition, the process CO2 emission during the same period based on the same datasets was also estimated. The results show that 21.02 Gt CO2 (95 % confidence interval, CI: 18.01–24.41 Gt CO2) had been absorbed in the cements produced from 1930 to 2019, with the 2019 annual figure mounting up to 0.89 Gt CO2 yr−1 (95 % CI: 0.76–1.06 Gt CO2). The cumulative uptake is equivalent to approximately 55 % of the process emission based on our estimation. In particular, China's dominant position in cement production or consumption in recent decades also gives rise to its uptake being the greatest, with a cumulative sink of 6.21 Gt CO2 (95 % CI: 4.59–8.32 Gt CO2) since 1930. Among the four types of cement materials, mortar is estimated to be the greatest contributor (approximately 59 %) to the total uptake. Potentially, our cement emission and uptake estimation system can be updated annually and modified when necessary for future low-carbon transitions in the cement industry. All the data described in this study, including the Monte Carlo uncertainty analysis results, are accessible at https://doi.org/10.5281/zenodo.4459729 (Wang et al., 2021).
- Article
(4393 KB) - Full-text XML
- BibTeX
- EndNote
According to the International Energy Agency (IEA) statistics, cement industry is the second-largest industrial CO2 emitter with a share of 27 % (2.2 Gt CO2 yr−1) in 2014 (IEA and WBCSD, 2018), and is estimated to account for approximately 7.4 % of the total anthropogenic CO2 emission in 2016 (Sanjuán et al., 2020). Broadly, there are two direct sources of CO2 emission originating from cement production: (1) the thermal decomposition of limestone (CaCO3) in the process of producing clinker; (2) the energy required for the decomposition, largely provided by combustion of fossil fuels. For the latter, energy efficiency improvement and cement kiln technology advancement have gained noticeable progress in recent years (Shen et al., 2016; Xu et al., 2014; Zhang et al., 2015). However, it has been widely estimated that the former so-called process emission constitutes most of the total direct emission (approximately 60 %). Consequently, the targeted reduction in emission of the cement industry for achieving climate action sustainable development goals (SDGs), which fully aligns with meeting the “below 1.5∘” climate target (Rogelj et al., 2018), hinges upon reducing process emission. Unfortunately, the traditional standardised ordinary Portland cement (OPC), which has been the dominant type of cement used by humans so far, has very high clinker content historically, i.e. high clinker-to-cement ratio (herein referred as clinker ratio). Both Marland et al. (1989) and Boden et al. (1995) reported the emission factor (EF) to be around 0.5 t CO2 t−1 cement then, which suggested an implicit clinker ratio > 95 %. On the other hand, since OPC clinkers are CaO-rich, a high clinker ratio would also increase the CO2 absorption capabilities (by carbonation) of cements. The main carbonation mechanisms that are responsible for the carbon uptake of cements can be attributed to their hydroxide and silicate constituents1, as described by Reactions (R1) and (R2):
Pan et al. (2020) recently studied the emission reduction potential from producing cement mortar and concrete blocks by mixing in a high level of alkaline blending (e.g. blast furnace slag, fly ash, and mine tailings) and discovered a yearly multi-gigatonne potential of CO2 abatement. Therefore, reducing the clinker ratio is still the key to lowering the process emission level of the cement industry, while the projected demand for cement is going to increase by a factor of 1.1–1.2 by the end of 2050 (IEA and WBCSD, 2018).
Andrew (2018) updated the global cement industry (process) emission inventory recently by using various data sources for different countries and time periods. The insufficient accounting for the geographically and temporally varying clinker ratio, as was embedded in prior estimation methods adopted by the Carbon Dioxide Information Analysis Centre (CDIAC) (Boden et al., 2017), was considered and corrected for. On the other hand, in our previous study on the uptake (Xi et al., 2016), clinker ratio values from the historical literature, including the default value of 0.75 (as the lower bound) recommended by the Intergovernmental Panel on Climate Change (IPCC) (Hanle et al., 2006), were used in our model for estimating the uptake as well as the uncertainty analysis by the Monte Carlo method. Therefore, updating the results by applying more realistic clinker ratio data is necessary, especially for China, where multiple surveys and reports have uncovered the strikingly lower-than-average clinker ratios post-1990.
In this study, we re-estimated the amount of CO2 uptake by cements produced from 1930 to 2019, including those used in concrete and mortar as well as those “lost” as construction waste and kiln dust. We updated the clinker ratio or production data after 1990 for China and treated India as a separate region. We estimated that 21.02 Gt CO2 (95 % confidence interval, CI: 18.01–24.41 Gt CO2) had been absorbed and sequestered in cements that had been produced between 1930 and 2019, which effectively abated 52 % of the corresponding process emission. The annual uptake in 2019 alone reached a staggering 0.89 Gt CO2 yr−1 (95 % CI: 0.76–1.06 Gt CO2 yr−1). Using this consistent framework and model, we could include regularly updated annual estimates of cement carbon uptake into annual assessments of the global carbon budget (GCB) (Friedlingstein et al., 2019) as an important anthropogenic carbon sink, which has not been thoroughly assessed or documented.
2.1 Cement and clinker production data resources and treatment
Global cement production data have been estimated by the United States Geological Survey (USGS) since the 1930s. In our previous study (Xi et al., 2016), we used USGS production data explicitly as the only source for calculations of the uptake. In addition, the world was geographically divided into four primary countries and aggregated regions, including China, the United States (US), Europe and central Eurasia (including Russia), and the rest of the world (ROW). We noticed that, other than Russia and Turkey, the country-specific European and central Eurasian cement production data were not available yet from the USGS after 2017. In this work, to keep the consistency with the prior geographical division and data source, 2018 and 2019 cement production data were projected for the “Europe and central Eurasia” region. Specifically, the average ratio of the production in Russia and Turkey to the total production in Europe and central Eurasia from 2013 to 2017 was taken as the scaling factor so that the total regional production for 2018 and 2019 can be projected, assuming this proportion remained the same. For the US, ROW, and China (prior to 1990), we continued to use the cement production data since 1930 from the USGS. The IPCC-recommended clinker ratios were continually used for these aggregated regions without extra fine-tuning to country-level data.
In terms of the updates on China, we first collected national cement production data for the period of 1990–2019 from the China Statistical Yearbook, available from the National Bureau of Statistics (NBS, 2019). To calculate the CO2 uptake based on our model (see Sect. 2.3 and 2.4), subject to data availability for different periods during 1990–2019, we then collected the clinker ratio data from various sources for the 1990–1999, 2000–2014, and 2015–2019 periods from the published literature (Gao et al., 2017; Xu et al., 2012, 2014), the China Cement Almanac (CCA; 2001–2015), and public national data from the Ministry of Information Technology (MIIT, 2019), respectively. As such, we also obtained the national clinker production for the 1930–2019 period. Additional progress we made in this work was to separate India from the ROW on the basis that India has now become the second-largest cement producer after China, with approximately 8 % of the world total in 2014 (IEA and WBCSD, 2018). Recent studies (Andrew, 2018, 2020) suggested that the average clinker ratio in India has been fluctuating in the past 3 decades. Therefore, we used the newly published year-by-year clinker ratio data for India for 1990–2019.
2.2 Estimating the process emission
Process CO2 emissions of the cement industry were estimated by multiplying regional clinker production by the derived process CO2 emission factors. Since the process CO2 emissions arise from chemical reactions involved in the production of clinker as carbonates (largely limestone, CaCO3) and are decomposed into oxides (largely lime, CaO) and CO2 by the addition of heat, they can be estimated by the conservation of the mass flow principle. The default value recommended by the IPCC is 510 kg CO2 t−1 clinker (Hanle et al., 2006), without considering emissions originating from MgCO3. In this study, we first collected local survey data by kiln type from the literature and applied them in the emission estimates. There are mainly five kiln types worldwide, including dry with preheater and precalciner, dry without preheater (long dry kiln), dry with preheater without precalciner, wet or shaft kiln, and semi-wet or semi-dry.
For China, a nationwide sampling survey of 359 cement production lines across 22 provinces was conducted (Shen et al., 2016), and we adopted the process CO2 emission factor estimated from this local Chinese study. As a result, we applied the sample-averaged emission factors: 519.66 kg CO2 t−1 clinker for dry with preheater without precalciner, dry with preheater and precalciner, and dry without preheater (long dry) kilns, and 499.83 kg CO2 t−1 clinker for semi-wet or semi-dry and wet or shaft kilns. For other countries in the absence of detailed survey data, we adopted the emission factors that were collected and summarised in Andrew (2018), which integrated local emission information for key countries (e.g. India). We then obtained annual country- or regional-level production technology information from the World Business Council for Sustainable Development (WBCSD) and the Global Cement Directory 2019 (publicly named as the GCD-2019 dataset). While the WBCSD collected technology-based clinker production information using a survey-based approach (IEA and WBCSD, 2018), the GCD-2019 dataset provides plant-level information of cement industries in service as of 2019 (for example, cement production capacity, physical address, number of kilns, cement production technology, etc.). We then cross-checked and integrated the “start of operation year” information at plant level from the “industryAbout” database (industryAbout, 2019) and various companies' websites. This information enabled us to infer the annual capacity-weighted production technology (i.e. kiln types) distributions for the 1930–2019 period. Finally, we used technology-weighted emission factors to calculate the regional-average emission factors, which were then used to estimate process CO2 emissions directly.
It is noted that in order to stay in line with the life-cycle CO2 uptake assessments of concrete structures, concrete construction waste, and cement kiln dust (CKD) in this study, in comparison to some previous studies (e.g. Andrew, 2018), our estimation framework for process CO2 emissions is relatively simple. Nevertheless, we integrated the global plant-level capacity and technology information into our estimates for the first time to provide new perspectives on emission estimates. In addition, we also assessed the uncertainties in such estimates using the Monte Carlo method.
2.3 Life-cycle uptake assessments of concrete structures
Here, we adhere to the breakdown of concrete utilisation into three stages as before (Xi et al., 2016): (1) service, (2) demolition, (3) secondary use. Therefore, the carbon uptake of concrete (Ccon) can be calculated as an aggregate of the three subcomponents:
where Cl,tl, Cd,td, and Cs,ts are the uptake during service, demolition, and secondary-use stage, respectively. The life cycle was deemed to be 100 years, in line with a historical study by Pade and Guimaraes (2007), considering that the longest average life of buildings in Europe is merely 70 years (Pommer and Pade, 2005). During concretes' service life, they are used primarily to build various functional buildings, roads, utilities, other public works, etc., hence exhibiting different sizes and geometrical shapes in the environment. We adopt a simplified approach by considering a three-dimensional diffusion “slab” model in which carbonation starts at the exterior side of the slab and gradually moves inwards: this is schematically shown in Fig. 1. According to Fick's second law, which is used in the calculation2, the carbonation depth is proportional to the square root of the carbonation time (tl) i.e. , linked by an apparent diffusion coefficient (ki). According to Reactions (R1) and (R2), in order to determine the amount of CO2 being absorbed during the carbonation processes, it is pivotal to work out the number of Ca cations in the cements; i.e. 1 mol Ca cation takes 1 mol of CO2. Similarly to what was recommended by the IPCC regarding the calculation of cement emission factor (), the theoretical carbon uptake of cements also depends on the clinker ratio () and on the CaO content in the clinker (). Additionally, in natural conditions, not all of the calcium in OPC would be associated with carbonation reactions due to its microstructural constraints (Lagerblad, 2005); hence the fraction of CaO that could be converted to CaCO3 (γ) should be considered, too, as follows:
where and MCaO are the molar mass of CO2 and CaO, respectively.
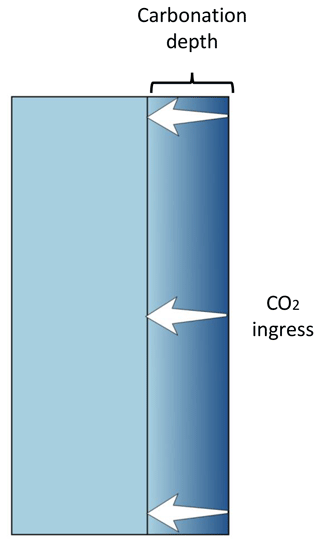
Figure 1A two-dimensional schematic representation (rectangular cross-section) of the three-dimensional “slab” carbonation model of concretes. The right-hand side that is close to the CO2 source is being carbonated first, with further carbonation taking place by CO2 diffusion in the cement.
In order to estimate the carbon uptake at macroscopic scale with the data available, we made the following simplifications: (1) assuming the diffusion front is equivalent to the carbonation front and the area behind the front is regarded to be fully carbonated3, (2) assuming the geometries of the cement parts resemble the slab shown in Fig. 1 so that the exposed surface area (Ai) can be calculated by the concrete volume in different structure categories and average thickness data. Further, since the carbonation rate depends on the environmental conditions, e.g. humidity and temperature, CO2 concentration, etc., and the concrete's physiochemical conditions, e.g. compressive strength, additives, surfacing, etc., we further broke down the utilisation of concrete based on these specifications (see https://doi.org/10.5281/zenodo.4459729; Wang et al., 2021). The region-specific calculations were then realised by regrouping the data based on their region-specific sources. Consequently, the regional and global uptakes can be calculated by aggregating each compressive strength class (i)4 as
where the common symbols keep their meanings as defined previously, and ci stands for the cement content of concrete. In short, on top of the regional cement production and/or clinker ratio data, other statistics necessary to carry out such regional calculations include (all regional) the proportion of cement used for making concrete (as opposed to mortar), the cement contents, the CaO content of clinker, the distribution of compressive strength class, and the average thickness of different concrete utilisations. Crucially though, diffusion coefficients of CO2 in concretes of the above specifications and the corresponding service lives will dictate how rapidly and for how long the uptake lasts. We conducted an extensive literature survey to collect the data needed on a regional basis and used collected datasets representative of Europe for ROW, apart from the concrete utilisation data, which we opted to apply to the Chinese situation5 and service lives, which we derived directly from the literature (see https://doi.org/10.5281/zenodo.4459729; Wang et al., 2021).
After their service life, concretes are usually demolished either for landfill or to be reused. Reusing concrete at the end of its service life has been encouraged and envisaged to reduce the total emissions and increase the sustainability of the cement industry (IEA and WBCSD, 2018). However, the reusing rate of demolished concrete had been found to be very low, at about 25 % worldwide (Kikuchi and Kuroda, 2011; Yang et al., 2014). Demolition entails crushing of the bulk concrete structures so that the embedded steel structures can be easily extracted and recycled; hence the end product is usually broken into pieces. Therefore, the surface area exposed to the air dramatically increases during the demolition stage. As pointed out earlier (Eq. 3), the exposed surface area is one of the key parameters that is positively correlated with the rate of carbonation; it is therefore expected that the carbon sequestered per unit time would increase with increasing exposure. Again, we simplified the geometrical aspects of the calculations by assuming that the demolished and crushed concrete parts ended up in spherical shapes so that the carbonation starts from the outer surface, moving inwards radially (see Fig. 2). Similarly, we considered the same diffusion model to be applied for the carbonation process. Based on the survey of typical crushed cement particle sizes, we divided the distributions into three distinct groups according to their respective minimum (a) and maximum diameters (b) in the range with respect to the maximum diameter (D0i) with which a particle will undergo full carbonation in compressive strength class i: (1) b≤D0i, (2) , (3) a> D0i. The corresponding methods for calculating their carbonated fraction (Fdi) then are as follows:
where kdi and td6are the diffusion coefficient of “exposed to air” condition for compressive strength class I and the time between service life and subsequent dealings. In addition, based on the survey data from the literature for the particle size, we assumed a uniform distribution between a and b for each reginal subcategory.
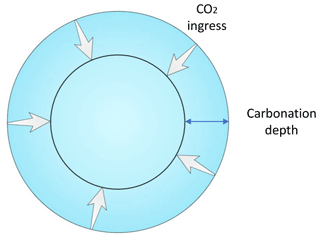
Figure 2Two-dimensional schematic representation (circular cross-section) of the three-dimensional “sphere” carbonation model of a concrete particle in the demolition stage.
Since carbonation during the demolition stage took place only in the bulk of concrete material, where it remains noncarbonated after used in service, the fraction of carbonated concrete before demolition should be excluded from the calculation to avoid double-counting. We assigned the total mass of consumed cement as mci7 and the carbonated cement in service life as , as in Eq. 3). Therefore, the total amount of CO2 uptake during the demolition stage () can be calculated as
Carbonation during the secondary-use stage that follows would be slower because a carbonate layer has formed at the particle surface previously. It might be less confusing to the readers to think of the demolition and secondary-use stages as a whole, with the diffusion process slowing down during the latter. Additionally, because of the high rates of landfill post-demolition, the diffusion processes are further retarded in the buried conditions8 (Papadakis et al., 1991; Yoon et al., 2007). Therefore, we introduce a lag time Δt because it would take longer for the carbonation to reach the same depth (ddi) when concrete particles are in the secondary-use conditions compared with the demolition conditions (tdi):
and we have
where the common symbols shared with Eq. (4) have the same meanings, and ksi stands for the diffusion coefficient during secondary use for compressive strength class i. By now, we can represent the combined carbonation depth of demolition and secondary-use stages with all known variables as
where tsi is the average time of the secondary-use stage9, and Dti is the maximum diameter with which a particle will undergo full carbonation in compressive strength class i in the demolition and secondary-use stages combined. Similarly to how we determined the fraction of carbonation previously, the fraction of further carbonation during the secondary-use stage can be calculated by integration according to the same set of particle size criteria:
Like for the demolition stage, where double-counting was avoided by excluding the carbonated concrete during service, calculating the carbonation during secondary use should be based on the noncarbonated fraction of concrete after the service and demolition stages. Accordingly, the carbon uptake during the last piece of the concrete life cycle can be expressed as follows:
where mdi stands for the mass of concrete carbonated during the demolition stage. Overall, Eq. (1) can be applied to obtain the total amount of CO2 absorbed based on the three stages as outlined above.
2.4 Kinetic-uptake models for other types of cement materials
2.4.1 Carbon uptake of cement mortar structures
Here, we adhere to the breakdown of mortar utilisation into three subcomponents as before (Winter and Plank, 2007; Xi et al., 2016): (1) rendering and plastering mortar, (2) masonry mortar, (3) maintenance and repairing mortar. Therefore, the total carbon uptake of mortar (Cmor) can be calculated as an aggregate of the three subcomponents:
where Crpt, Crmt, and Crmat are the uptake of the corresponding component, respectively. For each subcomponent, we conducted an extensive literature survey to collect the Chinese cement mortar utilisation category and percentage data. Additionally, since mortar carbonisation has not been quantified before as far as we are aware, we conducted experiments to measure the mortar carbonation rate coefficients and the proportion of CaO converted to CaCO3 of typical mortar cements produced in China and used these measured datasets as being representative of the other regions owing to a lack of data. Like concrete, mortar carbonation processes were also simplified to a two-dimensional diffusion “slab” model in which carbonation starts at the exterior of the slab and gradually moves inwards, and similarly, Fick's second law was applied to determine the carbonation depth in the general form. However, mortar cement diffusion rates (Km) were shown to be higher than concrete, which has a lower cement content, higher watercement ratios, and finer aggregate grains (El-Turki et al., 2009). The total mortar carbonation can be determined based on Eqs. (2) and (11), with the corresponding proportion of CaO conversion (γ1; see Eq. 14) adjusted to the mortar situation as measured. Again, we assumed the diffusion front is equivalent to the carbonation front, and the area behind the front was regarded to be fully carbonated.
The large exposure area and thin layers of mortar cement translate into rapid carbonation. We calculate annual mortar cement carbon uptake based on the proportion of annual carbonation depths of the utilisation thicknesses. The annual carbonation of mortar used for rendering, plastering, and decorating is calculated as follows:
where drp is the carbonation depth of rendering mortar; Km is the carbonation rate coefficient of cement mortar; t is the exposure time of rendering mortar after construction; frpt is the annual carbonation percentage of cement used for rendering mortar in year t; drpt and drp(t−1) are the carbonation depths of rendering mortar in year t and (t−1), respectively; dTrp is the utilisation thickness of rendering mortar; Crpt is the annual carbon uptake of carbonated rendering mortar; Wm is the amount of cement for producing mortar; rrp is the percentage of rendering mortar cement of total mortar cement; γ1 is the proportion of CaO within fully carbonated mortar cement that converts to CaCO3. After the carbonation depths in adjacent years were determined, the annual carbonation percentage was obtained by the difference between adjacent years to the total utilisation thickness. Combined with the cement for mortar and the percentage of mortar for rendering survey data, the annual carbonation of rendering mortar is then quantified. Calculation for carbon uptake of repairing and maintaining cement mortar is similar to rendering, plastering, and decorating mortar, with differences in the utilisation thickness and the percentage of mortar for repairing and maintaining.
In comparison to mortars for rendering and repairing, it takes longer for masonry mortar to complete carbonation due to the partially exposed condition, thicker utilisation layers, and their covering by rendering mortar on masonry wall surfaces. Here, we classify masonry walls into walls with both sides rendered (Cmbt), walls with one side rendered (Cmot), and walls without rendering (Cmnt). We conducted an extensive survey to collect data on the extents to which mortar rendering has been applied to masonry walls in China and used the representative data of China for other regions due to a lack of data. The carbon uptake of masonry mortar can be calculated as an aggregate of the three subcomponents:
where Cmbt, Cmot, and Cmnt are the uptake of the corresponding classification, respectively. The schematics of the carbonation models for the three situations mentioned are shown in Fig. 3; i.e. carbonation starts from the exterior rendering layer into the masonry layer when having a one- and two-side rendering layer or directly from the masonry layer and gradually moves inwards when there is no rendering.
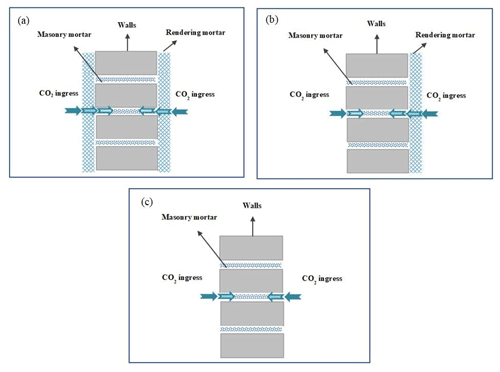
Figure 3Two-dimensional schematic representations (cross-section) of the carbonation model for masonry mortar. (a) Masonry mortar with two-side rendering carbonation takes place by diffusion from both rendering layers before reaching the masonry; (b) masonry mortar with one-side rendering carbonation takes place by CO2 diffusion from the rendering layer on one side and directly from the masonry on the other; (c) masonry mortar without rendering carbonation takes place by CO2 diffusion directly from the exterior of the masonry.
Based on the models outlined above, the calculation of masonry mortar carbonation is similar to rendering and repairing mortar in that determining the annual carbonation is according to the proportion of carbonation depth. The carbonation of masonry mortar for walls with both sides rendered is as follows:
where dmb is the total carbonation depth of masonry mortar of the wall with both sides rendered; t is the exposure time of masonry mortar after construction; tr is the time of full carbonation of rendering mortar of thickness dTrp; dTrp is the thickness of rendering mortar on masonry wall; fmbt is the annual carbonation percentage of cement used for masonry mortar with both sides rendered in year t; dmbt and dmb(t−1) are carbonation depth of masonry mortar with both sides rendered in year t and (t−1), respectively; dw is the thickness of masonry wall; tsl is the building service life; is the carbonation depth of a masonry mortar with both sides rendered in building service life; Cmbt is the annual carbon uptake of cement for masonry mortar with both sides rendered in year t; rrm is the percentage of masonry mortar cement in total mortar cement; rb is the percentage of masonry mortar with both sides rendered of total masonry mortar. For walls with both sides rendered, carbonation starts from the rendering exterior on both sides and gradually moves inward. When the utilisation time of masonry mortar is shorter than the time required for full carbonation of rendering mortar on the masonry wall, there is no chance for the underlying masonry to be exposed to CO2; hence carbonation should not happen. Otherwise, the fraction of carbonated rendering mortar on the surface should be excluded from the calculation to avoid double-counting. If the utilisation time of masonry mortar is longer than the time required for full carbonation of rendering mortar but shorter than the building service life, we used the ratio of the carbonation depth difference between adjacent years to the total thickness to show the carbonation fraction of masonry mortar with both sides rendered in year t. If the utilisation time of masonry mortar is longer than the building service life, it was assumed that the left noncarbonised masonry mortar will be fully carbonated in 1 year due to the large exposure area post-demolition. Therefore, the fraction of masonry mortar carbonation after the service life can be quantified by the difference between the fraction of masonry mortar carbonation during the service life (that is, the ratio of the carbonation depth during the service life to the total thickness) and the total masonry mortar carbonation of 100 %. The calculation for the carbonation of masonry mortar for walls with one side rendered differs only in the carbonation depth calculation; i.e. without rendering on one side, CO2 directly contacts the bare masonry mortar so that only the fraction of carbonated rendering mortar on one side was excluded. Similarly, for walls without rendering at all, CO2 directly contacts the bare masonry mortar from both sides so that the total carbonation depth is twice the carbonation depth on one side.
2.4.2 Uptake assessments of construction wastes
Cement wastes mainly arise during construction and accounts for 1 % to 3 % of total cement consumption according to construction budget standards (Zhou, 2003) and survey data (Lu et al., 2011). Most of this waste is in small pieces and will be recycled as backfill or landfilled after the completion of building projects; of these about 45 % is concrete, and 55 % is mortar (Bossink and Brouwers, 1996; Huang et al., 2013). Here, we adhere to the breakdown of construction wastes into two components as before: (1) construction waste mortar, (2) construction waste concrete. The carbon uptake of construction wastes (Cwaste) then can be calculated as an aggregate of the two subcomponents:
where Cwastecon and Cwastemor are the uptake of the corresponding component, respectively. Given the small piece sizes and hence large exposure area of the construction wastes, we made a few simplifications according to the literature survey: (1) assuming waste mortar completely carbonates in the first year, (2) assuming waste concrete completely carbonates over the following 5 years (ranging from 1 to 10 years) (Bossink and Brouwers, 1996; Huang et al., 2013). Consequently, the carbon uptake of construction wastes can be quantified by the annual carbonation fraction in line with the ratio of carbonation depths to the full carbonation depths. The expression of construction wastes carbonation is as follows:
where Wci is the cement used for concrete in strength class i, fcon is the loss rate of cement for concrete in construction stage, rcont is the annual carbonation fraction of construction waste concrete, Wmi is the cement used for mortar in strength class i, fmor is the loss rate of cement for mortar, and rmor is the annual carbonation fraction of construction waste mortar. In short, in addition to the regional cement production and clinker ratio data, other statistics needed to conduct the calculation include the distribution of compressive strength class, the loss rate of cement for concrete and mortar in the construction stage, and the carbonation time of construction wastes. Crucially though, the latter two statistics, for which we collected the data on a regional basis, will dictate the amount of carbon uptake.
2.4.3 Uptake assessments of cement kiln dust
Cement kiln dust (CKD) is the major by-product of the cement manufacturing process and has traditionally been considered to be industrial waste. Most of CKD is diverted to landfills, and a small part is beneficially reused (Khanna, 2009; USEPA, 1993). CKD is composed of fine, powdery solids and highly alkaline particulate material and is similar in appearance to Portland cement (Seo et al., 2019). Given the very small particle size (it predominantly ranges from a few micrometres to 50 µm, and some coarse particles are between 50–100 µm; Kaliyavaradhan et al., 2020), CKD full carbonation in landfill conditions can be achieved very rapidly within 1 year, and indeed substantial carbonation even occurs within the first 2 d of reaction (Huntzinger et al., 2009a, b; Siriwardena and Peethamparan, 2015). Therefore, the carbon uptake by CKD is calculated as follows:
where Wcem is the cement production, rCKD is the CKD generation rate based on clinker production, rlandfill is the proportion of CKD treatment in a landfill, is the CaO proportion in CKD (Siriwardena and Peethamparan, 2015), and γ2 is the fraction of CaO within fully carbonated CKD that has been converted to CaCO3. This equation stands because CKD carbonation effectively completes within 1 year.
2.5 Yearly and cumulative uptake calculations
While the sectoral carbon uptake can be analytically estimated by the corresponding sectoral equations, i.e. for concrete, mortar, construction waste, and CKD, respectively, using aggregated regional datasets as the inputs, the regional carbon uptake was determined by aggregating all sectoral contributions but with disaggregated regional production or consumption and diffusion or carbonation coefficient, concrete structure thickness, concrete strength distribution, mortar utilisation distribution, waste particle distribution, and CKD generating rate data, among others, as the model inputs. Consequently, the world total uptake can be divided up according to the usage of the cement produced as well as where the cement was produced/consumed.
For mortar cement, we explicitly showed how to determine the annual carbonation from Eqs. (12) to (14) and (16) to (18). Basically, for the carbon uptake of a specific year t, we can apply a simple subtraction of the cumulative values between adjacent years as
so that each year's contribution to the total carbonation can also be quantified. This way, we will be able to visualise the time lag in the carbonation process in that the uptake of a specific year t is not limited to the cement produced in the same year.
2.6 Uncertainty analysis
Based on the kinetic models described in previous sections, the annual regional carbon uptake was calculated by aggregating the contributions from individual types of cement. Likewise, the annual global carbon uptake was obtained from regional aggregation. It should be noted, though, that a Monte Carlo analysis method with 26 variables (see https://doi.org/10.5281/zenodo.4459729; Wang et al., 2021) was applied to evaluate the carbon uptake at each level; hence the annual median at a higher level (i.e. regional w.r.t. cement type and global w.r.t. regional) is not equal to the sum of its sublevel components. The variables associated with the estimates are mostly in common with our previous study (Xi et al., 2016), with the only difference being the distribution of the clinker ratio. Previously, the clinker ratio was set to range from 75 % to 97 % in a Weibull distribution with shape and scale parameters of 91.0 % and 25 for the years of 1990–2019. In this research, for China, based on previous studies and local survey data, we adjusted the corresponding uncertainty range for the 1990–2019 period. Specifically, for 1990–2004, the range of coefficient values of the clinker ratio was set to 10 %–20 %. In this range, the pseudo-random numbers were generated with a uniform distribution then multiplied by the mean values of clinker ratio to obtain the corresponding standard deviation. As such, the normally distributed random clinker ratio values were created. For 2004–2019, the random errors were calculated within the range of ±5 % of the mean values with a uniform distribution. For 1930–1989, the clinker ratio distribution was unchanged.
On the other hand, emission estimates are subject to uncertainties due to incomplete knowledge of activity levels and emission factors. In order to assess the uncertainties in our results more thoroughly, we conducted a comprehensive analysis of regional emission estimates. Following the method of previous studies (Tong et al., 2018; Zhao et al., 2011), we performed a Monte Carlo analysis that varied key parameters, including cement production, clinker ratio, and emission factors. The term “uncertainty” in this study refers to the lower and upper bounds of a 95 % confidence interval (CI) around our central estimate, i.e. median. All of the input parameters of activity levels and emission factors, with corresponding statistical distributions, were fed into a Monte Carlo framework, and 10 000 simulations were performed to analyse the uncertainties in estimated CO2 emissions. For the uncertainties in the regional process CO2 emission estimates, national-average emission factors were derived from previous studies and local survey databases (Andrew, 2018; Hanle et al., 2006; Shen et al., 2016), and we assumed these activity rates are normally distributed, with coefficients of variations (CVs; i.e. the standard deviation divided by the mean) ranging from 0.05 to 0.2 based on the specific data sources and year. Furthermore, the ranges of parameter values also vary by country, in part due to the quality of their statistical infrastructure.
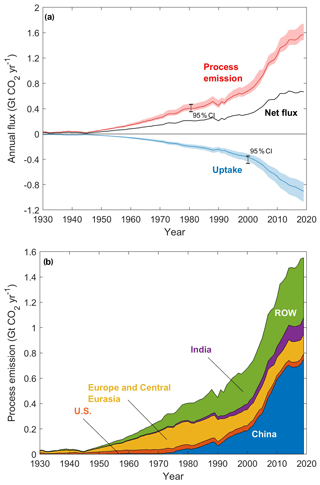
Figure 4(a) Annual CO2 process emission and uptake from producing and utilising cement materials from 1930 to 2019. The dotted lines denote the median values, while the respective shaded area denotes the 95 % confidence interval from Monte Carlo simulations. The net emission is also illustrated with the solid black line; (b) the country- and region-wise process CO2 emission (median) from 1930 to 2019.
3.1 Aggregated regional and global process emission
With the continued increase in the production of cement and associated clinker globally in the past few decades, the process CO2 emissions correspondingly have been increasing with limited abating measures (i.e. carbon capture and storage, CCS). According to our estimates, by 2019, the global process CO2 emissions reached 1.57 Gt yr−1 (95 % CI: 1.42–1.86 Gt) (see Fig. 4a), equivalent to about 25 % of the total CO2 emissions from industrial activities in 2018 (Tong et al., 2019). Cumulative emissions from 1930 to 2019 were estimated to be 38.22 Gt (95 % CI: 36.98–40.06 Gt), and more strikingly, more than 71 % of which have occurred since 1990. This finding agrees with other studies on cement carbon uptake using similar modelling approaches (Cao et al., 2020). From 1930 to 2019, with the rapid increase in cement demand (+5777 % of cement production increase during 1930–2019) driven by global industrialisation and urbanisation, the total process CO2 emissions correspondingly increased by a factor of about 49, which is actually slightly slower than the increase in production. This is partly due to the relative decreases in average clinker ratios (from ∼89 % in 1930 to ∼70 % in 2019) (Wang et al., 2021). Meanwhile, the regional attribution of such an increase changed significantly during the same period. As we can see in Fig. 4b, the process emission from cement produced in China and ROW (mainly comprising developing countries) gradually replaced the dominant roles of the US and Europe (and central Eurasia), while there has been considerable growth for India after the 2000s, contributing more than 85 % to the total emissions (1.42 Gt; 95 % CI: 1.34–1.59 Gt) in 2019 altogether. Specifically, China alone emitted more than half (∼ 53 %, 0.75 Gt; 95 % CI: 0.69–0.89 Gt), and India, as the second-largest cement production country in the world, emitted ∼ 10 % of the total process emissions of the cement industry as of 2019.
As mentioned in Sect. 2.2, there are other studies estimating the process emission based on high-resolution, national-level clinker ratio data. Andrew (2019) reported the process emission in 2017 to be 1.48 ± 0.20 Gt CO2 and that aggregated over 1928–2017 to be 36.9 ± 2.3 Gt CO2. Using our simpler region-based approach yields a 2017 process emission of 1.37 Gt CO2 (95 % CI: 1.30–1.53 Gt CO2), while the 1930-2017 cumulative process emission is 35.3 Gt CO2 (95 % CI: 32.8–40.5 Gt CO2). The results are very similar, and unsurprisingly our estimates have a greater level of uncertainty due to our coarser disaggregation of geographic regions.
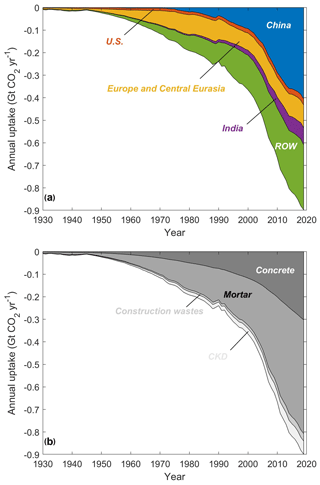
Figure 5Annual global uptake (median) by cement materials by (a) country or region and (b) type from 1930 to 2019. The uptake is projected onto the y axis as negative values, denoting absorption as opposed to emission.

Figure 6The increase in cement CO2 uptake in China, India, Europe and central Eurasia, the US, and the rest of the world from 1930 to 2019. The y axes are plotted in logarithm scale (absolute value) and within the same range for comparison; both the median (dotted lines) and 95 % CI (shaded area) are shown.
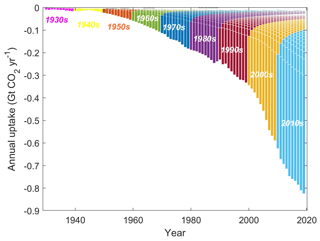
Figure 7The cumulative characteristic of carbon uptake of cement. The colour-coded bar areas represent the amount of uptake by the cement produced/consumed in each decade from 1930 to 2019. The fractions of uptake that occurred in each decade post-1990 are annotated. The “tails” indicate that cement produced in a certain time will keep absorbing CO2 beyond its production or consumption, and the annual uptakes are composed of current and historical contributions.
3.2 Cement carbon uptake by region and material type
Global CO2 uptake by cement materials in 2019 reached 0.89 Gt (95 % CI: 0.76–1.06 Gt) according to our estimates, of which cement consumed in China contributed about 0.40 Gt. Cumulatively speaking, China, as a country, also made the greatest contribution, mounting up to 6.21 Gt CO2 (95 % CI: 4.59–8.32 Gt CO2). This is clearly illustrated in Fig. 5a, where the area representing each region denotes the amount of uptake. In the US and Europe, since the cement stock per capita has reached saturation (Cao et al., 2017), and the concrete structures generally have long service lives (70 and 65 years for Europe and the US on average, respectively) relative to the life cycle (i.e. 100 years) considered in our model, it is conceivable that the absolute uptake in these two regions only increased mildly after the 1980s, which is in drastic contrast to the “exponential” rise observed for China (see Fig. 6). In terms of ROW, the increase in uptake has been somewhat intermediate between the case for China and developed nations, reflecting their relatively milder increase in cement production or consumption as compared with China, yet far from saturation as well as relatively shorter building service lives as compared with the US and Europe. On the other hand, although cements have been predominantly used for making concretes worldwide, mortar had absorbed more CO2, reaching 12.34 Gt (95 % CI: 9.99–14.97 Gt) cumulatively according to our estimates. This is mainly attributed to the faster carbonation kinetics of mortar compared with concrete, manifested by the higher diffusion coefficients, thinner layers of mortar cement, and large exposure area in our model as supported by our own experimental measurements (see https://doi.org/10.5281/zenodo.4459729; Wang et al., 2021) and the literature (Lutz and Bayer, 2010; Winter and Plank, 2007).
3.3 Characteristics of cement carbon uptake
One of the limitations of natural carbonation for carbon capture is that it is a slow process; hence speeding up the chemical processes involved is the key to realising tangible impacts on mitigating CO2 emissions. This is also the case for cement materials, especially concrete structures, which took up the majority of their utilisation. Therefore, the carbon uptake by concretes, before demolition, persisted during their lifetimes. This is evident in Fig. 7, where the cement materials (mainly concretes) consumed in a given decade (colour-coded) still made a contribution to carbon uptake decades later. In spite of this feature, more than 71 % of the total uptake was attributed to, based on our estimates, the cement materials produced/consumed after the 1990s. This is in line with the trend of process emission growth, i.e. 73 % for the post-1990 era in the same 1930–2019 period. The difference10 can be accounted for by the dynamic processes and the varying durations of the stages involved in the life cycles, as considered and implemented in the uptake models. This contrasts with the immediate process emission process. It is also suggested in Fig. 7 that a surge in uptake occurs at the demolition stage because of the significant increase in fresh surface area. Figure 8 more evidently demonstrates such an effect by showing the sudden increase in uptake in the late 2000s owing to the concrete produced/consumed historically. This can be traced back to the 1930s–1940s, when the majority of cement was produced and consumed in Europe, where the average service life of concrete structures is set as 70 years in our model.
All the original datasets used for estimating the emission and uptake in this study and the resulting datasets themselves from the simulation as well as the associated uncertainties are made available by Zenodo at https://doi.org/10.5281/zenodo.4459729 (Wang et al., 2021).
Estimating CO2 uptake of cements is essential for evaluating the real environmental impact of the cement industry. Previous efforts were limited by data availabilities and incomplete accounting for other cement materials other than concrete. From a historical perspective, while mortar had absorbed more CO2 than any other type of cement, more uptake had occurred in China than in any other country, owing to its dominant cement production or consumption position in recent decades (> 43 % from 2000 to 2019). The kinetic processes dictate that CO2 uptake of cement is a dynamic process such that legacy absorption from cements produced in the past should not be omitted. Overall, the post-1990 era sees more than 75 % of the total uptake estimated. As a revision to our previous work (Xi et al., 2016), where the clinker ratios were likely to have been overestimated, a dynamic clinker ratio approach was adopted to reflect the recent technological changes in the industry despite being limited to China and India only. In addition, the dynamic clinker ratios were also applied in re-evaluating the process emissions. The compounded results suggest that the cumulative CO2 uptake reached 21.02 Gt (95 % CI: 18.01–24.41 Gt), offsetting approximately 55 % of the corresponding process emission as of 2019. The offset level is noticeably higher than our previous estimate for 1930–2015 (∼ 43 %), while the uptake for the same period is broadly similar: 4.8 GtC from this study as opposed to 4.5 GtC from the previous one (Xi et al., 2016), indicating internal consistency of the uptake model and a direct relationship between cement clinker content and process emission.
This dataset and the estimation methodology can serve as a set of tools to assess the emission and, more importantly, the uptake of CO2 by cement materials during their life cycles. Given that cement demand is projected to continue to increase to satisfy society developments globally, future work is crucially needed to increase the accuracy of the uptake estimates by utilising the direct clinker production data where possible and obtaining spatially resolved conversion factors determined by experiments.
RG prepared, reviewed, and edited the manuscript with assistance from JW, PC, SJD, and RMA. RG performed the analyses with support from JW and LB on analytical approaches. JW curated the datasets. DT, LB, and FX developed the code and performed the simulations with support from RG, JW, DT, and RMA on datasets. FX and ZL conceptualised and supervised the study.
The authors declare that they have no conflict of interest.
Jiaoyue Wang and Fengming Xi acknowledge funding from the Youth Innovation Promotion Association, Chinese Academy of Sciences (grant nos. 2020201 and 2016180). Fengming Xi acknowledges funding from the National Natural Science Foundation of China (grant no. 41977290); the CAS President's International Fellowship for Visiting Scientists (grant no. 2017VCB0004); the Liaoning Xingliao Talents Project (grant no. XLYC1907148); and the Liaoning Hundred, Thousand and Ten Thousand Talent Project. Zhu Liu acknowledges funding from the National Natural Science Foundation of China (grant nos. 71874097 and 41921005), the Beijing Municipal Natural Science Foundation (grant no. JQ19032), and the Qiushi Foundation.
This research has been supported by the National Natural Science Foundation of China (grant nos. 71874097, 41921005, and 41977290), the CAS President's International Fellowship Initiative (grant no. 2017VCB0004), the Beijing Municipal Natural Science Foundation (grant no. JQ19032), and the Liaoning Xingliao Talents Project (grant no. XLYC1907148).
This paper was edited by David Carlson and reviewed by two anonymous referees.
Andrew, R. M.: Global CO2 emissions from cement production, 1928–2017, Earth Syst. Sci. Data, 10, 2213–2239, https://doi.org/10.5194/essd-10-2213-2018, 2018.
Andrew, R. M.: Global CO2 emissions from cement production, 1928–2018, Earth Syst. Sci. Data, 11, 1675–1710, https://doi.org/10.5194/essd-11-1675-2019, 2019.
Andrew, R. M.: Timely estimates of India's annual and monthly fossil CO2 emissions, Earth Syst. Sci. Data, 12, 2411–2421, https://doi.org/10.5194/essd-12-2411-2020, 2020.
Boden, T. A., Marland, G., and Andres, R. J.: Estimates of Global, Regional, and National Annual CO2 Emissions from Fossil-Fuel Burning, Hydraulic Cement Prduction, and Gas Flaring: 1950–1992 (NDP-030/R6), Oak Ridge, available at: https://cdiac.ess-dive.lbl.gov/epubs/ndp/ndp030/ndp0301.htm (last access: 1 April 2020), 1995.
Boden, T. A., Marland, G., and Andres, R. J.: Global, Regional, and National Fossil-Fuel CO2 Emissions, Oak Ridge, TN, United States, 2017.
Bossink, B. A. G. and Brouwers, H. J. H.: Construction Waste: Quantification and Source Evaluation, J. Constr. Eng. Manag., 122, 55–60, https://doi.org/10.1061/(ASCE)0733-9364(1996)122:1(55), 1996.
Cao, Z., Shen, L., Løvik, A. N., Müller, D. B., and Liu, G.: Elaborating the History of Our Cementing Societies: An in-Use Stock Perspective, Environ. Sci. Technol., 51, 11468–11475, https://doi.org/10.1021/acs.est.7b03077, 2017.
Cao, Z., Myers, R. J., Lupton, R. C., Duan, H., Sacchi, R., Zhou, N., Reed Miller, T., Cullen, J. M., Ge, Q., and Liu, G.: The sponge effect and carbon emission mitigation potentials of the global cement cycle, Nat. Commun., 11, 3777, https://doi.org/10.1038/s41467-020-17583-w, 2020.
China Cement Association (CCA): China Cement Almanac, China Building Industry Press, Beijing, China, 2001–2015.
El-Turki, A., Carter, M. A., Wilson, M. A., Ball, R. J., and Allen, G. C.: A microbalance study of the effects of hydraulicity and sand grain size on carbonation of lime and cement, Constr. Build. Mater., 23, 1423–1428, https://doi.org/10.1016/j.conbuildmat.2008.07.006, 2009.
Friedlingstein, P., Jones, M. W., O'Sullivan, M., Andrew, R. M., Hauck, J., Peters, G. P., Peters, W., Pongratz, J., Sitch, S., Le Quéré, C., Bakker, D. C. E., Canadell, J. G., Ciais, P., Jackson, R. B., Anthoni, P., Barbero, L., Bastos, A., Bastrikov, V., Becker, M., Bopp, L., Buitenhuis, E., Chandra, N., Chevallier, F., Chini, L. P., Currie, K. I., Feely, R. A., Gehlen, M., Gilfillan, D., Gkritzalis, T., Goll, D. S., Gruber, N., Gutekunst, S., Harris, I., Haverd, V., Houghton, R. A., Hurtt, G., Ilyina, T., Jain, A. K., Joetzjer, E., Kaplan, J. O., Kato, E., Klein Goldewijk, K., Korsbakken, J. I., Landschützer, P., Lauvset, S. K., Lefèvre, N., Lenton, A., Lienert, S., Lombardozzi, D., Marland, G., McGuire, P. C., Melton, J. R., Metzl, N., Munro, D. R., Nabel, J. E. M. S., Nakaoka, S.-I., Neill, C., Omar, A. M., Ono, T., Peregon, A., Pierrot, D., Poulter, B., Rehder, G., Resplandy, L., Robertson, E., Rödenbeck, C., Séférian, R., Schwinger, J., Smith, N., Tans, P. P., Tian, H., Tilbrook, B., Tubiello, F. N., van der Werf, G. R., Wiltshire, A. J., and Zaehle, S.: Global Carbon Budget 2019, Earth Syst. Sci. Data, 11, 1783–1838, https://doi.org/10.5194/essd-11-1783-2019, 2019.
Gao, T., Shen, L., Shen, M., Liu, L., Chen, F. and Gao, L.: Evolution and projection of CO2 emissions for China's cement industry from 1980 to 2020, Renew. Sust. Energ Rev., 74, 522–537, https://doi.org/10.1016/j.rser.2017.02.006, 2017.
Hanle, L., Maldonado, Pedro Onuma, E., Milos, T., and van Oss, H. G.: 2006 IPCC – Guidelines for National Greenhouse Gas Inventories: Industrial Processes and Product Use, available at: https://www.ipcc-nggip.iges.or.jp/public/2006gl/vol3.html (last access: 10 August 2020), 2006.
Huang, T., Shi, F., Tanikawa, H., Fei, J., and Han, J.: Materials demand and environmental impact of buildings construction and demolition in China based on dynamic material flow analysis, Resour. Conserv. Recy., 72, 91–101, https://doi.org/10.1016/j.resconrec.2012.12.013, 2013.
Huntzinger, D. N., Gierke, J. S., Kawatra, S. K., Eisele, T. C. and Sutter, L. L.: Carbon dioxide sequestration in cement kiln dust through mineral carbonation, Environ. Sci. Technol., 43, 1986–1992, https://doi.org/10.1021/es802910z, 2009a.
Huntzinger, D. N., Gierke, J. S., Sutter, L. L., Kawatra, S. K., and Eisele, T. C.: Mineral carbonation for carbon sequestration in cement kiln dust from waste piles, J. Hazard. Mater., 168, 31–37, https://doi.org/10.1016/j.jhazmat.2009.01.122, 2009b.
Hyvert, N., Sellier, A., Duprat, F., Rougeau, P., and Francisco, P.: Dependency of C-S-H carbonation rate on CO2 pressure to explain transition from accelerated tests to natural carbonation, Cem. Concr. Res., 40, 1582–1589, https://doi.org/10.1016/j.cemconres.2010.06.010, 2010.
IEA and WBCSD: Technology Roadmap: Low-Carbon Transition in the Cement Industry, IEA, Paris, available at: https://www.iea.org/reports/technology-roadmap-low-carbon-transition-in-the-cement-industry (last access: 22 August 2020), 2018.
industryAbout: World – Cement Industry Map, available at: https://www.industryabout.com/world-cement-industry-map (last access: 22 August 2020), 2019.
Kaliyavaradhan, S. K., Ling, T. C., and Mo, K. H.: Valorization of waste powders from cement-concrete life cycle: A pathway to circular future, J. Clean. Prod., 268, 122358, https://doi.org/10.1016/j.jclepro.2020.122358, 2020.
Khanna, O. S.: Characterization and utilization of cement kiln dusts (CKDs) as partial replacements of Portland cement – NASA/ADS, University of Toronto, available at: https://ui.adsabs.harvard.edu/abs/2009PhDT .252K/abstract (last access: 31 July 2020), 2009.
Kikuchi, T. and Kuroda, Y.: Carbon Dioxide Uptake in Demolished and Crushed Concrete, J. Adv. Concr. Technol., 9, 115–124, https://doi.org/10.3151/jact.9.115, 2011.
Lagerblad, B.: Carbon dioxide uptake during concrete life cycle – State of the art, Cement och Betong Institutet, Stockholm, 47 pp., 2005.
Lu, W., Yuan, H., Li, J., Hao, J. J. L., Mi, X., and Ding, Z.: An empirical investigation of construction and demolition waste generation rates in Shenzhen city, South China, Waste Manag., 31, 680–687, https://doi.org/10.1016/j.wasman.2010.12.004, 2011.
Lutz, H. and Bayer, R.: Dry Mortars, in: Ullmann's Encyclopedia of Industrial Chemistry, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim, Germany, 2010.
Marland, G., Boden, T. A., Griffin, R. C., Huang, S. F., Kanciruk, P., and Nelson, T. R.: Estimates of CO2 emissions from fossil fuel burning and cement manufacturing, based on the United Nations energy statistics and the US Bureau of Mines cement manufacturing data, Oak Ridge, TN, United States, 1989.
MIIT: Building materials, available at: http://www.miit.gov.cn/n1146312/n1146904/n1648356/n1648361/index.html (last access: 22 August 2020), 2019.
NBS: National data, available at: https://data.stats.gov.cn/ (last access: 22 August 2020), 2019.
Pade, C. and Guimaraes, M.: The CO2 uptake of concrete in a 100 year perspective, Cem. Concr. Res., 37, 1348–1356, https://doi.org/10.1016/j.cemconres.2007.06.009, 2007.
Pan, S. Y., Chen, Y. H., Fan, L. S., Kim, H., Gao, X., Ling, T. C., Chiang, P. C., Pei, S. L. and Gu, G.: CO2 mineralization and utilization by alkaline solid wastes for potential carbon reduction, Nat. Sustain., 3, 399–405, https://doi.org/10.1038/s41893-020-0486-9, 2020.
Papadakis, V. G., Vayenas, C. G., and Fardis, M. N.: Experimental investigation and mathematical modeling of the concrete carbonation problem, Chem. Eng. Sci., 46, 1333–1338, https://doi.org/10.1016/0009-2509(91)85060-B, 1991.
Pommer, K. and Pade, C.: Guidelines – Uptake of carbon dioxide in the life cycle inventory of concrete, Danish Technological Institute, ISBN: 87-7756-757-9, 2005.
Rogelj, J., Shindell, D., Jiang, K., Fifita, S., Forster, P., Ginzburg, V., Handa, C., Kheshgi, H., Kobayashi, S., Kriegler, E., Mundaca, L., Séférian, R. and Vilariño, M. V.: Mitigation Pathways Compatible with 1.5 ∘C in the Context of Sustainable Development, available at: https://www.ipcc.ch/site/assets/uploads/sites/2/2019/02/SR15_Chapter2_Low_Res.pdf (last access: 2 September 2020), 2018.
Sanjuán, M. Á., Andrade, C., Mora, P., and Zaragoza, A.: Carbon Dioxide Uptake by Cement-Based Materials: A Spanish Case Study, Appl. Sci., 10, 339, https://doi.org/10.3390/app10010339, 2020.
Seo, M., Lee, S.-Y., Lee, C., and Cho, S.-S.: Recycling of Cement Kiln Dust as a Raw Material for Cement, Environments, 6, 113, https://doi.org/10.3390/environments6100113, 2019.
Shen, L., Zhao, J., Wang, L., Liu, L., Wang, Y., Yao, Y., Geng, Y., Gao, T., and Cao, Z.: Calculation and evaluation on carbon emission factor of cement production in China, Chinese Sci. Bull., 61, 2926–2938, https://doi.org/10.1360/N972016-00037, 2016.
Siriwardena, D. P. and Peethamparan, S.: Quantification of CO2 sequestration capacity and carbonation rate of alkaline industrial byproducts, Constr. Build. Mater., 91, 216–224, https://doi.org/10.1016/j.conbuildmat.2015.05.035, 2015.
Tong, D., Zhang, Q., Davis, S. J., Liu, F., Zheng, B., Geng, G., Xue, T., Li, M., Hong, C., Lu, Z., Streets, D. G., Guan, D., and He, K.: Targeted emission reductions from global super-polluting power plant units, Nat. Sustain., 1, 59–68, https://doi.org/10.1038/s41893-017-0003-y, 2018.
Tong, D., Zhang, Q., Zheng, Y., Caldeira, K., Shearer, C., Hong, C., Qin, Y., and Davis, S. J.: Committed emissions from existing energy infrastructure jeopardize 1.5 ∘C climate target, Nature, 572, 373–377, https://doi.org/10.1038/s41586-019-1364-3, 2019.
USEPA: Cement Kiln Dust Report to Congress, available at: https://archive.epa.gov/epawaste/nonhaz/industrial/special/web/html/cement2.html (last access: 31 July 2020), 1993.
Wang, J. Y., Bing, L. F, Tong, D., Guo, R., and Xi, F. M.: Global CO2 uptake of cement in 1930–2019 (Version 3) [Data set], Zenodo, https://doi.org/10.5281/zenodo.4459729, 2021.
Winter, C. and Plank, J.: The European dry-mix mortar industry (Part 1), ZKG Int., 60, 62–69, 2007.
Xi, F., Davis, S. J., Ciais, P., Crawford-Brown, D., Guan, D., Pade, C., Shi, T., Syddall, M., Lv, J., Ji, L., Bing, L., Wang, J., Wei, W., Yang, K. H., Lagerblad, B., Galan, I., Andrade, C., Zhang, Y., and Liu, Z.: Substantial global carbon uptake by cement carbonation, Nat. Geosci., 9, 880–883, https://doi.org/10.1038/ngeo2840, 2016.
Xu, J. H., Fleiter, T., Eichhammer, W., and Fan, Y.: Energy consumption and CO2 emissions in China's cement industry: A perspective from LMDI decomposition analysis, Energ. Policy, 50, 821–832, https://doi.org/10.1016/j.enpol.2012.08.038, 2012.
Xu, J. H., Fleiter, T., Fan, Y., and Eichhammer, W.: CO2 emissions reduction potential in China's cement industry compared to IEA's Cement Technology Roadmap up to 2050, Appl. Energy, 130, 592–602, https://doi.org/10.1016/j.apenergy.2014.03.004, 2014.
Yang, K. H., Seo, E. A., and Tae, S. H.: Carbonation and CO2 uptake of concrete, Environ. Impact Assess. Rev., 46, 43–52, https://doi.org/10.1016/j.eiar.2014.01.004, 2014.
Yoon, I. S., Çopuroglu, O., and Park, K. B.: Effect of global climatic change on carbonation progress of concrete, Atmos. Environ., 41, 7274–7285, https://doi.org/10.1016/j.atmosenv.2007.05.028, 2007.
Zhang, S., Worrell, E., and Crijns-Graus, W.: Evaluating co-benefits of energy efficiency and air pollution abatement in China's cement industry, Appl. Energy, 147, 192–213, https://doi.org/10.1016/j.apenergy.2015.02.081, 2015.
Zhao, Y., Nielsen, C. P., Lei, Y., McElroy, M. B., and Hao, J.: Quantifying the uncertainties of a bottom-up emission inventory of anthropogenic atmospheric pollutants in China, Atmos. Chem. Phys., 11, 2295–2308, https://doi.org/10.5194/acp-11-2295-2011, 2011.
Zhou, H.: Construction and Installation Engineering Budget Manual, China Machine Press, 2003.
Other minor phases including ettringite also contribute to the overall carbonation (Hyvert et al., 2010).
Other more sophisticated diffusion models have not been widely accepted or verified.
As opposed to the concept of “partly carbonated”, where reaction kinetics are considered.
Four class strengths are considered, including C15, C16–C23, C24–C35, > C35.
The rationale is that ROW is mainly comprised of developing nations; hence it is more likely that the utilisation of concrete adopts similar patterns to China.
The average value was estimated to be 0.4 years worldwide (Pade and Guimaraes, 2007).
The cement consumed was taken to be the same as the cement produced. The discrepancies were considered in the uncertainty analysis.
Demolished concretes that are subsequently landfilled and recycled as backfill aggregates are assumed to be devoid of further carbonation.
Since the life cycle of concrete is assessed on a 100-year basis, .
It is not necessarily the case that the fraction of uptake is smaller than that of the process emission for the post-1990 era.