the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A European map of groundwater pH and calcium
Borja Jiménez-Alfaro
Ondřej Hájek
Lisa Brancaleoni
Marco Cantonati
Michele Carbognani
Anita Dedić
Daniel Dítě
Renato Gerdol
Petra Hájková
Veronika Horsáková
Florian Jansen
Jasmina Kamberović
Jutta Kapfer
Tiina Hilkka Maria Kolari
Mariusz Lamentowicz
Predrag Lazarević
Ermin Mašić
Jesper Erenskjold Moeslund
Aaron Pérez-Haase
Tomáš Peterka
Alessandro Petraglia
Eulàlia Pladevall-Izard
Zuzana Plesková
Stefano Segadelli
Yuliya Semeniuk
Patrícia Singh
Anna Šímová
Eva Šmerdová
Teemu Tahvanainen
Marcello Tomaselli
Yuliya Vystavna
Claudia Biţă-Nicolae
Michal Horsák
Water resources and associated ecosystems are becoming highly endangered due to ongoing global environmental changes. Spatial ecological modelling is a promising toolbox for understanding the past, present and future distribution and diversity patterns in groundwater-dependent ecosystems, such as fens, springs, streams, reed beds or wet grasslands. Still, the lack of detailed water chemistry maps prevents the use of reasonable models to be applied on continental and global scales. Being major determinants of biological composition and diversity of groundwater-dependent ecosystems, groundwater pH and calcium are of utmost importance. Here we developed an up-to-date European map of groundwater pH and Ca, based on 7577 measurements of near-surface groundwater pH and calcium distributed across Europe. In comparison to the existing European groundwater maps, we included several times more sites, especially in the regions rich in spring and fen habitats, and filled the apparent gaps in eastern and southeastern Europe. We used random forest models and regression kriging to create continuous maps of water pH and calcium at the continental scale, which is freely available also as a raster map (Hájek et al., 2020b; https://doi.org/10.5281/zenodo.4139912). Lithology had a higher importance than climate for both pH and calcium. The previously recognised latitudinal and altitudinal gradients were rediscovered with much refined regional patterns, as associated with bedrock variation. For ecological models of distribution and diversity of many terrestrial ecosystems, our new map based on field groundwater measurements is more suitable than maps of soil pH, which mirror not only bedrock chemistry but also vegetation-dependent soil processes.
- Article
(12914 KB) - Full-text XML
-
Supplement
(1078 KB) - BibTeX
- EndNote
The Earth system is currently undergoing unprecedented changes in climate, global biogeochemical cycles and land use, resulting in biodiversity loss (Ceballos et al., 2017; Song et al., 2018; Blowes et al., 2019; Brondizio et al., 2019). Freshwater systems belong to the most endangered habitats (Cantonati et al., 2020a; Tickner et al., 2020), and, among them, groundwater-dependent ecosystems, such as fens and springs, hold primacy (Janssen et al., 2016; Chytrý et al., 2019; Hájek et al., 2020a; Stevens et al., 2020). Species composition and richness of spring systems are generally governed by water pH and calcium concentration (Ca2+), which are highly variable at different spatial scales (Malmer, 1986; Rydin et al., 2013; Peterka et al., 2017; Horsáková et al., 2018; Cantonati et al., 2020a, b). Therefore, understanding the spatial patterns in groundwater pH and Ca2+ is important not only for general geochemical knowledge and for water resource management but also to the same extent for the conservation of freshwater systems and associated biodiversity.
In Earth and biodiversity sciences, ecological modelling is a widely used tool for understanding the distribution and diversity patterns of ecosystems and habitats and for predicting their future development under global change. Ecological models usually incorporate environmental or historical predictors extracted from thematic maps (Jiménez-Alfaro et al., 2018a; Večeřa et al., 2019; Divíšek et al., 2020), including soil properties for terrestrial ecosystems (Hengl et al., 2017). However, soil parameters such as soil pH contribute negligibly to the models for groundwater-dependent habitats, even for those strongly controlled by pH and Ca2+, such as base-rich fens (Jiménez-Alfaro et al., 2018b). This is due to a poor correlation between groundwater chemistry and pH or Ca2+ in soil, disrupted mainly by mineral leaching or accumulation of organic matter in soil. For this reason, there is a strong need to produce maps for groundwater pH and Ca2+ concentration at the European scale that would allow for producing the continental-scale ecological models useful for enforcing conservation strategies in groundwater-dependent habitats. Ideally, such models should include lithology as a dominant factor determining groundwater pH and Ca2+ concentration (Hem, 1985; Chapelle, 2003; Tahvanainen; 2004; Stevens et al., 2020).
In spite of important mapping efforts of groundwater (Duscher et al., 2015) and karst aquifers (Chen et al., 2017) at the European and global level, the only available European-scale maps of groundwater pH and Ca2+ concentration are those included in the FOREGS (Forum of European Geological Surveys) Geochemical Atlas of Europe (Salminen et al., 2006). These maps are based on 808 stream-water measurements distributed relatively equally across Europe. However, they show a large gap in eastern and southeastern Europe (Romania, Bulgaria, Belarus, the Russian Federation, Ukraine, Moldova, Serbia, Kosovo, Montenegro, Bosnia and Herzegovina, and North Macedonia). In addition, those maps are based on insufficient data density in some areas rich in groundwater-dependent ecosystem types but heterogeneous in terms of lithology (the Alps, the Carpathians, Bohemian Massif, the Cantabrian Mountains and the Pyrenees, and some regions of Fennoscandia). We therefore aimed at substantial improvement of the existing data by creating a database with field data measurements across the entire European continent and at creating a model-based map representing major patterns of groundwater pH and Ca2+ concentration at local and continental scales. Our data will allow for a better understanding of the patterns and causes of groundwater conditions in freshwater systems, strongly improving the spatial information suitable for European-scale modelling of biodiversity in groundwater-dependent and related ecosystems.
2.1 Data collection
We assembled the data set of pH and Ca2+ (or electrical conductivity in µS cm−1 at 20 ∘C; hereinafter abbreviated as EC) measurements in groundwater, covering the whole of Europe, with a greater density in the regions rich in endangered groundwater-dependent ecosystems such as springs and fens. We excluded most of Ukraine and the European part of the Russian Federation because of large data gaps in these areas. We considered all types of shallow groundwater systems, especially spring, spring fen and stream water. The core of our data set is formed by unpublished pH and Ca2+ or EC data sets of the co-authors (3618 sites); some of them were processed in ecological papers without having presented original pH and Ca2+ data (Hájková et al., 2006, 2008; Hájek et al., 2008; Sekulová et al., 2013; Plesková et al., 2016; Horsáková et al., 2018; Šímová et al., 2019). The second most important source were vegetation databases registered in GIVD (Global Index of Vegetation‐Plot Databases; Dengler et al., 2011; Table 1) and EVA (European Vegetation Archive; Chytrý et al., 2016), from where 1160 measurements from freshwater habitats were obtained. Both unpublished data and data from vegetation databases were filtered using original information or metadata of the sources in a way that only data from spring-fed fens and springs were considered. The data from ombrotrophic bogs and clearly topogenic fens (mainly terrestrialised lakes) were omitted because their water chemistry is governed by the decomposition of organic matter, atmospheric humidity and deposition, algal photosynthesis (Kann and Smith, 1999), and biotic processes such as cation exchange capacity of mosses (Clymo, 1963; Soudzilovskaia et al., 2010; Vicherová et al., 2015) rather than by bedrock chemistry. We also obtained data from public data sets stored in national environmental and nature conservation agencies of Germany, Slovenia and Bulgaria (1081 sites; see Table 1); data from the FOREGS Geochemical Atlas of Europe (Salminen et al., 2006; 808 sites); and literature data based on our gap-oriented excerption (883 sites; Table 1); most data came from Hinterlang (1992), Tanneberger et al. (2011), Eades et al. (2018), Kadūnas et al. (2017) and Savić et al. (2017).
In total, we collected 7577 samples (Table 1). Some of these samples are repeated measurements conducted in the same site, especially in public data sets, while other samples (from vegetation databases or literature data) share the same coordinates and site name or code, suggesting repeated measurements as well. We therefore averaged repeated measurements from the same sampling sites. We further deleted samples whose coordinates were obviously erroneous, such as those in oceans. These steps reduced the number of samples to 6561, out of which 6459 samples contained information on the water pH, and 5927 samples contained information about EC of water or Ca2+ concentration. Out of these 5927 samples, 2988 had directly measured both Ca2+ and EC (µS cm−1 at 20 ∘C), and for the remaining 2939 samples we estimated the Ca2+ concentration by EC of water.
2.2 Imputation of missing Ca2+ values by EC of water
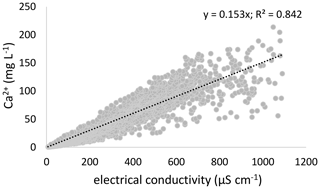
For imputation of Ca2+ values based on EC, we first aimed at constructing a simple imputation equation based on the well-known correlation between EC and the Ca2+ concentration in springs and fens (Hem, 1985; Sjörs and Gunnarsson, 2002; Plesková et al., 2016). In our data set of 2988 samples, as well as in its regional subsets, this relationship was strongly governed by EC values above ca. 1000 µS cm−1, although they formed only a small part of the data set (4.7 % of the data set; 139 samples). In the EC range of 1000–10 000 µS cm−1 (an outlier of 17 000 µS cm−1 was omitted), the correlation between water EC and the Ca2+ concentration was not statistically significant (r = 0.15, p = 0.07). The problem of high EC values governing the regression model was the most apparent in the public data sets. In the data set of the Bulgarian Ministry of Environment and Water, weak correlation between EC and Ca2+ persisted even when EC values above 1000 were omitted (Fig. S1 in the Supplement). This database further contains many samples which are not near-surface samples that were measured in other datasets. We therefore finally decided (1) not to include the database of the Bulgarian Ministry of Environment and Water into the imputation model and (2) limit the gradient of EC to 1000 µS cm−1. We further omitted a few samples from ophiolite (Kamberović et al., 2019) where high EC occurred despite low Ca2+. The resulting data set of 2319 samples nevertheless still showed some samples with a suspiciously high or low Ca2+ concentration relative to EC (Fig. S2 in the Supplement), suggesting either the effect of ions other than Ca2+ or an inconsistent analytical methodology. Because our aim was to create the most accurate imputation model rather than test the relationship, we removed these outliers. Therefore, we calculated the EC:Ca and Ca:EC ratios and removed outliers, i.e. all points larger than 1.5 times the interquartile range. The final imputation model was hence based on 2062 sites. We performed a null-intercept linear regression (Fig. 1) with Ca2+ as a dependent variable (y) and EC as a predictor (x); the resulting equation of y = 0.153x was obtained (R2 = 0.84). Such a relationship between Ca2+ and EC is similar to that found in the abovementioned studies (Hem, 1985; Sjörs and Gunnarsson, 2002; Plesková et al., 2016). Based on this equation, we imputed Ca2+ concentrations to all samples where only EC was measured. The imputed Ca2+ values show a somewhat narrower range (Fig. S3 in the Supplement) than originally measured values. Both subsets show a minimum Ca2+ value below 1 mg L−1, but imputed data show a lower non-outlier maximum (125.5 mg L−1) than measured data (197.2 mg L−1). The absolute maximum value was also lower for the subset with imputed values. Imputation of Ca2+ values to all samples, including high EC ones (> 1000 µS cm−1), hence did not skew the imputed data to higher values.
2.3 Geographical modelling and selection of the predictors
We used our dataset with measured groundwater pH and either measured or imputed Ca2+ concentrations to model expected values across non-sampled areas. Our aim was to produce continuous maps for groundwater-dependent pH (GW-pH) using 6459 samples (pH min = 2.20; max = 11.32; mean = 6.69) and groundwater-dependent Ca2+ (GW-Ca) using 5927 samples (min = 0.15; max = 3567.41; mean = 48.73 mg L−1). Ca2+ values were ln-transformed. All field samples had geographic coordinates assigned from GPS or georeferenced with an accuracy between ca. 10 m (precise field measurements) and 500 m (from georeferenced sites in databases). We kept the pH outliers: 10 values below 3.5 and 9 values above 8.8. Even if these values may be suspicious, they largely come from published sources (FOREGS Geochemical Atlas of Europe and the British vegetation database). Apart from measurement error, they may be explained by the influence of mineral waters from deep hydrological circulations (e.g. in a spring in the Apennines, a very high pH value of 11.2 was due to enrichment with sodium and chloride associated with a low-temperature reaction between meteoric water and ultramafic rocks; Boschetti and Toscani, 2008; Boschetti et al., 2013; Segadelli et al., 2017; Cantonati et al., 2020c). These values form only a minor part of the data set and have a negligible effect on the results.
For each site, we obtained environmental predictors from thematic GIS (geographic information system) maps (see below). We focused on the predictors that may causally affect the groundwater pH and calcium concentration. Aquifer chemistry is of prime importance (Hem, 1985; Fairchild et al., 1994; Frei et al., 2000; Chapelle, 2003; Tahvanainen, 2004; Stevens et al., 2020), but no such thematic map exists, at least not at the scale needed for computing our spatial predictions. We therefore included the lithological groups from the Hydrogeological Map of Europe (Duscher et al., 2015), together with soil pH maps (see below), for which we anticipated a certain correlation with bedrock chemistry. Apart from aquifer chemistry, residence time may also affect groundwater chemistry by impacting dissolution rates. Precipitation amount and frequency affect not only flow paths activity and redistribution of groundwater but also its residence time in the aquifer, impacting carbonate dissolution and precipitation rates (Hem, 1985; Crossman et al., 2011; Lewandowski et al., 2015; Vystavna et al., 2020). Groundwater with a short transit time (1–3 years) or “young water” (Soulsby et al., 2015) can be particularly sensitive to changes in precipitation amount and frequency. We therefore also considered climatic parameters associated with precipitation in the models (see below). Although there are some other potential predictors of minor importance that may affect groundwater chemistry (Hem, 1985; Stevens et al., 2020), no corresponding thematic map is available to be included into our models. For some sites, the selected predictors were missing in the maps (e.g. sites at the far north in the Arctic zone or close to the sea or water bodies), and these sites were therefore not included in the final models. We finally collected topographic data to test the potential effect of elevation and slope as indirect factors potentially influencing groundwater chemistry.
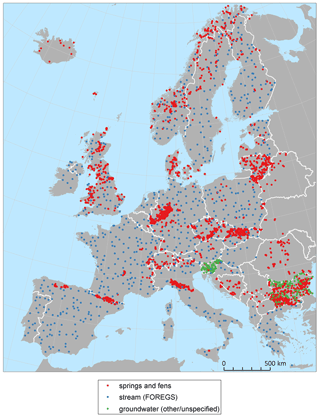
Figure 2Spatial distribution of the three groups of calibration data collected for modelling groundwater pH and Ca2+ in European fens (original and literature data from springs and fens; data from streams from the FOREGS Geochemical Atlas of Europe; other data). Other data include public data from national groundwater monitoring in Bulgaria and Slovenia. For separate maps of pH and Ca2+ see Fig. S5 in the Supplement.
2.4 Numerical analyses
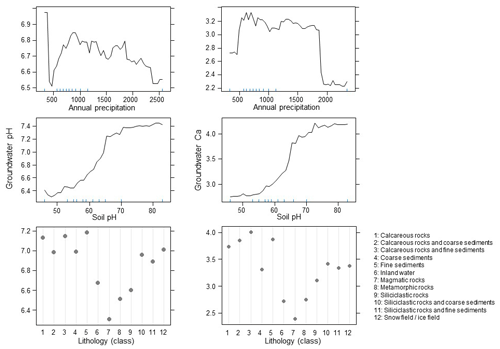
Numerical analyses were done in R version 3.6.3 (R Core Team, 2020), with the support of ArcGIS 10.2 (Esri, Redlands, CA, USA) for geoprocessing and map production. We first conducted exploratory analyses to test the prediction ability of GIS layers related to soil bedrock, climate and topography on the variation of both Ca and pH. We focused on layers with a complete coverage of Europe, with an eastern border of the Black Sea in Turkey to the White Sea in the Russian Federation, thus including the regions with a relatively good cover of field measurements (Fig. 2). We performed linear models for individual variables to select those providing significant relationships and > 1 % of explained variance. A variable for soil pH (measured in water solution) at 15 cm depth for a 250 m grid resolution provided by the SoilGrids project (https://www.soilgrids.org, last access: June 2020) had the highest explanatory power for GW-pH (R2 = 0.22) and GW-Ca (R2 = 0.16). The same results were obtained when using the same variable for 5 or 10 cm depth. We also tested soil estimates from Ballabio et al. (2019), but they provided weaker relationships for both GW-pH (R2 = 0.14 using soil pH as a predictor) and GW-Ca (R2 = 0.01 using soil pH; R2 = 0.01 using soil CaCO3). To account for lithology, we used the lithological groups (litho3 level, identifying 12 major classes; see Fig. 4) included in the polygon layer of the Hydrogeological Map of Europe (Duscher et al., 2015) as a categorical variable. We also selected annual precipitation (coded as Bio12) as provided in CHELSA (Climatologies at high resolution for the earth's land surface areas; Karger et al., 2017) to account for precipitation gradients which are expected to influence groundwater regimes. Other CHELSA variables related to precipitation were highly correlated with annual precipitation (Pearson r > 0.75) and omitted. Slope and elevation showed negligible effects on both GW-pH and GW-Ca (linear regression, adjR2 < 0.05, p < 0.001). Since preliminary models showed no differences when these variables were included, they were discharged.
The variables of lithology and soil pH were aggregated to the same grid extent of CHELSA at 1 km resolution, as this is the most appropriate scale to balance the original scales of both layers. This grid extent is also the most suitable spatial scale to be used in the context of further ecological modelling, which is in many cases combined with climatic data from e.g. CHELSA or WorldClim (http://www.worldclim.org, last access: June 2020) for making temporal climatic projections. The lithological map (originally at 1 : 1 500 000 scale, which corresponds to a raster resolution of ca. 1 km) was converted to a grid resolution using the dominant unit. Soil pH was converted from the original 250 m to 1 km grid resolution using a bilinear interpolation to create a smooth surface based on the weighted average of the four nearest cells.
Because even the combination of the selected variables might not lead to a precise fine-scale indication of aquifer chemistry, we further employed a kriging approach to data analysis, assuming an effect of spatial correlation to estimate the values close to the original samples. The final spatial predictions were therefore based on regression kriging (RK), a technique that combines a regression model based on explanatory variables with the interpolation of model residuals with ordinary kriging (Hengl et al., 2007; Meng et al., 2013). RK is especially appropriate for modelling soil attributes at medium and large scales, combining the spatial autocorrelation of soil variables with the explanatory power of auxiliary variables (Keskin and Grunwald, 2018). We implemented RK with the “GSIF” R package (Hengl, 2020). As the regression component, we computed random forests, since a preliminary analysis with our data showed better performance than linear models, generalised linear models or generalised additive models. Random forests are ensemble learning methods based on decision trees and an internal correction of overfitting, which provide high interpretability and good performance when compared with other algorithms used in soil spatial modelling (Wiesmeier et al., 2011). Another advantage of random forests is that they have no requirements for considering the probability distribution of soil variables, fitting complex non-linear relationships for spatial extrapolation (Hengl et al., 2015) that ultimately improve the spatial predictions. We fitted the random forest model and the residual variogram for groundwater pH and Ca2+ separately using the function fit.gstatModel() in the “GSIF” package. Effect plots for the predictors were created for the same models using the partial() function in the “pdp” package (Greenwell, 2017). Spatial predictions were then computed with the predict() function using the model object generated previously and a 5-fold cross-validation. Model evaluation was based on the calculation of the mean error (ME) and the root mean squared error (RMSE) as the differences between predicted and observed values (Keskin and Grunwald, 2018; Pham et al., 2019). We compared the relationships between the models produced for both groundwater pH and Ca2+ by using a random sampling of 5000 points to extract cell values and computing a Pearson correlation. To assess regional differences, we correlated values grouped in 25 neighbouring cells of each single cell using the rasterCorrelation() function in the “spatialEco” R package (Evans, 2020).
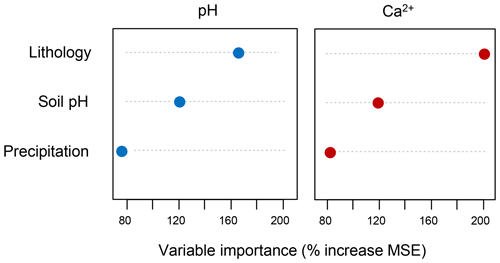
Figure 3Variable importance of random forest models computed for groundwater pH and Ca2+. MSE: mean standard error.
In measured data, ranges and medians of pH and Ca2+ concentration were similar across Europe (Fig. S4 in the Supplement), with the lowest pH values found in the Atlantic and Iberian regions and the highest pH values found in southern Europe except the Iberian Peninsula. The lowest Ca2+ values were found in boreal Europe, while the highest were found in central and southern Europe. The random forest models computed with the lithology, soil pH and precipitation explained 40 % and 55 % of the variance for GW-pH and GW-Ca, respectively. Lithology was the variable with the highest importance in both models (Fig. 3), although its effect was higher in the model computed for Ca2+ than for pH. These effects were mainly associated with the lithological units reflecting calcareous bedrock, followed by categories with coarse and fine sediments such as flysch (Fig. 4). Soil pH had a higher relative importance in GW-pH than GW-Ca, although in both cases the variable had a similar positive effect. Finally, annual precipitation had the lowest contributions in the two models (Fig. 3), with both Ca2+ and pH dropping suddenly after the threshold of annual precipitation of ca. 1800 mm (Fig. 4), although the highest pH values occur under the lowest precipitation and tend to decrease towards high-precipitation areas.
When adding the kriging component, model predictions reached 65 % and 74 % of explained variance for GW-pH and GW-Ca, respectively. The mean values of standard errors (SEs; 0.0006 for pH; −0.0009 for Ca) and root mean squared errors (RMSEs; 0.588 for pH; 0.690 for Ca) were higher in the models for pH, but in both cases they showed low values that suggest accurate predictions, in agreement with their total explained variance.
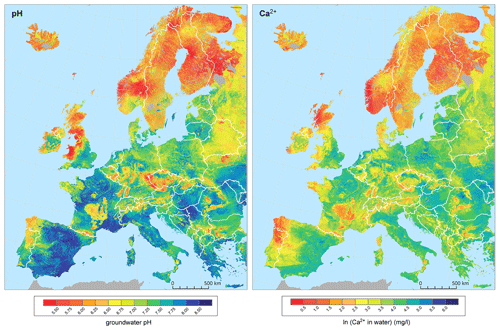
Figure 5Model predictions based on regression kriging. Note that the Ca2+ concentration is on an ln scale. The map was created entirely by the authors with state borders from ArcGIS® version 10.2 (Esri, Redlands, CA, USA).
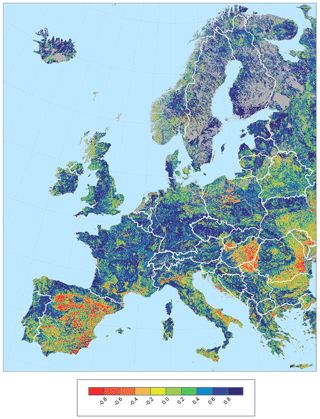
Figure 6Spatial correlation between the models computed for groundwater pH and Ca2+. Values show the Pearson correlation coefficient computed over every single cell by using a sampling of 25 neighbouring cells. The map was created entirely by the authors with state borders from ArcGIS® version 10.2 (Esri, Redlands, CA, USA).
Model predictions for GW-pH reflected the lowest values in Scandinavia, Iceland, the northern UK, and some regions of central and eastern Europe (Fig. 5). The highest values were predicted in eastern Iberia and many regions of central and eastern Europe, although a big part of the study area was dominated by neutral pH values (6 to 7). The spatial patterns for GW-Ca (Fig. 5) were rather similar to pH. The overall correlation between the two models was 0.83 (Pearson r, p < 0.001), but they showed differences in some regions. This was supported by the spatial correlation computed for each cell (Fig. 6), reflecting different magnitudes of correlation across the study area, especially in the eastern Iberian Peninsula and southeastern Europe.
4.1 Spatial patterns in groundwater pH and Ca2+ concentration in Europe
As expected, the values of water pH and Ca2+ concentration are largely shaped by lithology in groundwater-dependent habitats across Europe. Indeed, it has been recognised by regional studies that the distribution of major spring and fen habitats, of which the species composition largely depends on pH and Ca2+, is well determined by bedrock type (Hájek et al., 2002; Tahvanainen, 2004; Hinterlang, 2017; Peterka et al., 2017; Cantonati et al., 2020c). Since the European-scale geological map we used here is not precise enough to capture differences in bedrock chemistry within the major lithological units that are defined largely by geological stratification, the contribution of soil pH in the model probably also reflected lithological variation, as soil pH generally correlates with regional bedrock chemistry (Chadwick and Chorover, 2001). On the other hand, soil pH is also affected by climate-dependent pedogenesis, which incorporates a climate-zonal geographical component in this effect (Duchaufour, 2012; Maxbauer et al., 2017).
Precipitation is another determinant of groundwater chemistry in our study. High annual precipitation above ca. 1800 mm obviously reduced an interaction time of groundwater with Ca2+ and carbonates deposited in rocks (Fairchild et al., 1994; Segadelli et al., 2017; Cantonati et al., 2020b), resulting in lower Ca2+ concentration in groundwater. This effect is more pronounced in snowy regions, where seasonal snowmelt modulates the recharge patterns of groundwater. The duration of the snowmelt period can impact the occurrence and dynamic of preferential flow and prolong or reduce the interaction of the seepage with soil and bedrock materials (Mohammed et al., 2019). We therefore suggest that fast hydrological pathways and a short transit time driven by snowmelt and precipitation can explain the lowest Ca2+ values in hyper-oceanic cold regions of southwestern Norway or western Scotland. It may further explain lower pH and Ca2+ values on windward slopes of high mountains, even if bedrock is moderately calcium-rich. Nevertheless, understanding the complementary effects of precipitation and slope will need to account for more accurate models based on GPS data, better precipitation data and high-resolution (< 250 m) topographic predictors.
The resulting pattern at the European scale is governed by the strong latitudinal and altitudinal gradients, i.e. decreasing pH and Ca2+ northwards and regionally also towards mountain regions. This pattern largely follows bedrock chemistry, with crystalline rocks prevailing and most carbonate rocks being eroded by glaciers, in high latitudes and altitudes. The excess of precipitation over evaporation and theoretically also slower weathering rates in colder regions (White and Blum, 1995) contribute as well. Although this pattern is well known (Økland et al., 2001; Hájek et al., 2006; Hinterlang, 2017; Peterka et al., 2017) and has been captured also by the FOREGS Geochemical Atlas of Europe (Salminen et al., 2006), our improved model provides much finer regional patterns. In southern Europe, low pH and Ca2+ values were modelled in the Pyrenees, the Balkans, southwestern Corsica and Calabria, i.e. the regions where boreal or endemic types of fen communities occur as relicts (Chytrý et al., 2020). The Alps, the Apennines, the Carpathians and the Baltic region show a fine-scaled mosaic of alkaline (calcium-rich) and acidic (calcium-poor) groundwater that contributes to the high diversity and conservation value of groundwater-dependent ecosystems, such as fens (Cantonati et al., 2009, 2011; Gerdol et al., 2011; Joosten et al., 2017; Horsáková et al., 2018). The most apparent “acidic island” in central Europe is located in the southwestern part of the Bohemian Massif (Czech Republic and Germany), where acidic types of springs and fens are quite frequent, and some studies further document anthropogenic acidification on siliceous bedrock in the 1970s and 1980s, which has re-emerged recently because of extreme climatic events (Kapfer et al., 2012; Schweiger et al., 2015). It is, however, possible that particularly this acidic island is picked out mainly because of the high amount of available data.
Clearly, most of Fennoscandia is markedly acidic and calcium-poor mainly due to glacial history. Yet, the model identified small alkaline- and calcium-enriched islands in northeastern and central Sweden and northwestern Norway which are associated with rare types of calcareous fen and spring communities (Dierssen, 1982; Vorren et al., 1999; Udd et al., 2015; Miller et al., 2021). More localised pockets of calcareous habitats are however known from most parts of Fennoscandia that are not recognised with the grain of our European-wide analysis. With our results, the future modelling of diversity and distribution of individual habitat types of groundwater-dependent wetlands will be more reliable. Regionally rare habitat conditions will be recognised better, and the disentangling of climate and pH effects will be more feasible.
4.2 Data gaps and further improvements
Although being based on the hitherto most comprehensive field data set currently available, the presented map cannot be considered definitive. Surely there are many pH and EC or Ca2+ measurements conducted across Europe that we could not include into the data set because they are hardly accessible. Except for the Russian Federation and Moldova, the largest gaps still occur in the southern parts of the Pannonian Plain (southeastern Hungary, northern Serbia and western Romania), southeastern Belarus and eastern Ukraine. We have available some data from the latter region (Vystavna et al., 2015; Table S2 in the Supplement), but a large gap in the rest of the data set prevented reliable geospatial modelling. These data might be used in future updates of the map once the gap in central Ukraine is filled. The lack of data in the Pannonian Plain has led to a poor correlation between predicted pH and Ca2+ values (Fig. 4). Such a poor correlation and sometimes low density of data apply also for some other lowland regions, such as the Danube Plain in southern Romania; Po Valley in Italy; and valleys around the Douro, Ebro and Tagus rivers in Spain. Apart from eutrophication, this pattern may be caused by the imbalanced distribution of groundwater-dependent habitat types in our data set. Unlike mountain regions, the data for these lowlands were largely taken from the FOREGS Geochemical Atlas of Europe (Salminen et al., 2006) and national groundwater databases, i.e. largely from stream water. Considering the major purpose of our map (creating new data sources for ecological modelling of fens and springs) these regions are less crucial for biodiversity modelling because they have largely been transformed to arable land or they are too dry. On the other hand, caution is needed when interpreting the maps in an ecological sense. The extremely high pH (> 8) and Ca2+ (ln [Ca2+] > 4; i.e. Ca2+ > 55 mg L−1) values that occur in lowlands visually govern the map, but for ecological differentiation of groundwater-dependent habitats in Europe the differences within the middle part of the gradient, i.e. between pH 5.5 and 7.0, are much more important (Malmer, 1986; Wheeler and Proctor, 2000; Hájek et al., 2006; Rydin et al., 2013).
Our data set is expected to be amended in the future, as more studies will be published and more data will be available, so further versions will be accessible in the open repository. New data will help to improve predictions for those regions with a relatively lower sampling effort and also those with lithologically heterogeneous landscapes. Future updates of the model may also focus at finer spatial resolutions (e.g. 100 to 250 m), but this will require an increase of the spatial accuracy of the calibration data and the predictor variables, as in some central European areas (Le et al., 2019; Chuman et al., 2019). Although we tested several variables with a potential predictive effect on groundwater pH and Ca, many of them had lower explanatory power (e.g. Ballabio et al., 2019), or they were redundant with the soil pH layer we used (i.e. previous versions of SoilGrids using the same data sources). The low predictive value of other predictors with potential predictive value, like slope, elevation or another precipitation variable, is probably related to their broad spatial scale, with values averaged at 1 km grid resolution having little impact to discriminate groundwater variation at the landscape level (Jiménez-Alfaro et al., 2018b). This contrasts with the predictive value of the lithological layer, which is however based on a similar spatial (but originally vectorial) resolution. However, lithological bedrock is generally more homogeneous at the landscape scale, with the only exception of certain geologically complex regions. These findings suggest that future improvements of our models will depend on the quality of new lithological (or related soil chemistry) variables with a direct effect on groundwater pH and Ca. We also note that the lithological map we used here is simplified to large units, while many regional and national geological maps are being produced at finer resolutions. The combination of such new predictors with accurate calibration data at the continental level and at fine-scale resolution seems the most likely opportunity to produce significantly better models, since the influence of spatially dependent (kriging) effects is rather limited by the distribution of sample points.
The dataset of georeferenced pH and EC measurements and the resulting maps in GIS-compatible format (shapefile) are accessible at https://www.zenodo.org/ (last access: March 2021); https://doi.org/10.5281/zenodo.4139912 (Hájek et al., 2020b).
No original R code was used; the used codes are cited.
Here, we provide the first European map of groundwater pH and Ca2+ content. We collected field measurements, distributed as evenly as possible, of water pH and Ca2+ or EC from European groundwater-dependent habitats, with a relatively higher sampling effort in regions rich in endangered groundwater-dependent ecosystems (springs and fens). Despite the general high accuracy of our models, we note that prediction uncertainties may affect the reliability of models computed with both random forests and kriging (Hengl et al., 2018; Szatmári and Pásztor, 2019). Another source of prediction uncertainty is related to the quality of the original chemical measurements and the georeferentiation of their geographic position. Moreover, the predictor variables rely on spatial models (soil pH and precipitation) or broad geographic maps (lithology) which are based on their own uncertainties and assumptions. Future improvements of groundwater pH and Ca estimates should therefore consider a more accurate set of response variables and fine-scale predictors, preferably including lithology and soil pH (i.e. variables surrogating bedrock chemistry) and precipitation sum (i.e. residence time of groundwater). Despite potential uncertainties and data gaps, this study uses an unprecedented combination of data to provide freely accessible and realistic maps that can be used in any kind of spatial modelling, showing a better resolution and fewer gaps than previously published maps. The character of our input data, which are also freely accessible, predetermines our map to be used in ecological modelling to address the distribution and diversity of groundwater-dependent ecosystems and associated species. We even believe that our maps could be also suitable for ecological modelling of habitats other than those which are groundwater-dependent. It may mirror the bedrock chemistry better than the map of soil pH because soil pH is a resultant of pedogenetic processes, which are tightly associated with the character of the vegetation cover itself (Miles, 1985; Duchaufour, 2012). We conclude that our European maps of near-surface groundwater pH and EC provides the best solution currently available for modelling the biodiversity of groundwater-dependent ecosystems, especially at the continental or supra-regional scale.
The supplement related to this article is available online at: https://doi.org/10.5194/essd-13-1089-2021-supplement.
MH and BJA contributed equally to the paper. They conceived the research, collected data and led the writing process. BJA designed and executed models for both the random forest and regression kriging. OH prepared the input data and final map outputs. All authors provided unpublished data and commented on the paper.
The authors declare that they have no conflict of interest.
This work was supported by the Czech Science Foundation (grant no. 19-01775S provided support for Borja Jiménez-Alfaro, Petra Hájková, Veronika Horsáková and Michal Horsák; grant no. GX19-28491X to the Centre for European Vegetation Syntheses provided support for Michal Hájek, Tomáš Peterka and Ondřej Hájek). Jutta Kapfer was supported by the Fram Center (grant no. A36214). We thank Sabine Bergmann and Dirk Hinterlang (State Agency for Nature, Environment and Consumer Protection North Rhine-Westphalia, Germany) and Rossitza Gorova (Ministry of Environment and Water of Bulgaria) for providing us with the public water chemistry data, Andraž Čarni for alerting us to the open data on Slovenian groundwater, and Valerijus Rašomavičius for providing us with the data from Kadūnas et al. (2017). We thank Tatyana Ivchenko for providing us with the data for the Ural Mountains, which were not included in the paper. Paweł Pawlikowski (P.P.), Lucia Sekulová (L.S.), Jana Navrátilová (J.N.) and Dag-Inge Øien (D.-I.Ø.) kindly agreed for us to use their unpublished pH and EC data. We further thank Ilona Knollová, John Rodwell (J.R.), Kiril Vasilev (K.V.) and Idoia Biurrun (I.B.) for providing pH data from vegetation databases via the European Vegetation Archive.
This research has been supported by the Czech Science Foundation (grant nos. 19-01775S and GX19-28491X) and the Fram Center (grant no. A36214).
This paper was edited by Jens Klump and reviewed by two anonymous referees.
Ballabio, C., Lugato, E., Fernández-Ugalde, O., Orgiazzi, A., Jones, A., Borrelli, P., Montanarella, L., and Panagos, P.: Mapping LUCAS topsoil chemical properties at European scale using Gaussian process regression, Geoderma, 355, 113912, https://doi.org/10.1016/j.geoderma.2019.113912, 2019.
Blowes, S. A., Supp, S. R., Antão, L. H., Bates, A., Bruelheide, H., Chase, J. M., Moyes, F., McGill, B., Magurran, A., Myers-Smith, H., Winter, M., Bjorkman, A. D., Bowler, E., Byrnes, J. E. K., Gonzalez, A., Hines, J., Isbell, F., Jones, H. P., Navarro, L. M., Thompson, P. L., Vellend, M., Waldock, C., and Dornelas, M.: The geography of biodiversity change in marine and terrestrial assemblages, Science, 366, 339–345, https://doi.org/10.1126/science.aaw1620, 2019.
Boschetti, T. and Toscani, L.: Springs and streams of the Taro-Ceno Valleys (Northern Apennine, Italy): Reaction path modeling of waters interacting with serpentinised ultramafic rocks, Chem. Geol., 257, 76–91, https://doi.org/10.1016/j.chemgeo.2008.08.017, 2008.
Boschetti, T., Etiope, G., Pennisi, M., Romain, M., and Toscani, L.: Boron, lithium and methane isotope composition of hyperalkaline waters (Northern Apennines, Italy): Terrestrial serpentinisation or mixing with brine?, Appl. Geochem., 32, 17–25, https://doi.org/10.1016/j.apgeochem.2012.08.018, 2013.
Brondizio, E. S., Settele, J., Díaz, S., and Ngo, H. T.: Global assessment report on biodiversity and ecosystem services of the Intergovernmental Science-Policy Platform on Biodiversity and Ecosystem Services, IPBES Secretariat, Bonn, Germany, available at: https://ipbes.net/global-assessment (last access: March 2021), 2019.
Cantonati, M., Van de Vijver, B., and Lange-Bertalot, H.: Microfissurata gen. nov. (Bacillariophyta), a new diatom genus from dystrophic and intermittently-wet terrestrial habitats, J. Phycol., 45, 732–741, https://doi.org/10.1111/j.1529-8817.2009.00683.x, 2009.
Cantonati, M., Lange-Bertalot, H., Decet, F., and Gabrieli, J.: Diatoms in very-shallow pools of the site of community importance Danta di Cadore Mires (south-eastern Alps), and the potential contribution of these habitats to diatom biodiversity conservation, Nova Hedwigia, 93, 475–507, https://doi.org/10.1127/0029-5035/2011/0093-0475, 2011.
Cantonati, M., Poikane, S., Pringle, C. M., Stevens, L. E., Turak, E., Heino, J., Richardson, J. S., Bolpagni, R., Borrini, A., Cid, N., Čtvrtlíková, M., Galassi, D. M. P., Hájek, M., Hawes, I., Levkov, Z., Naselli-Flores, L., Saber, A. A., Di Cicco, M., Fiasca, B., Hamilton, P. B., Kubečka, J., Segadelli, S., and Znachor, P.: Characteristics, main impacts, and stewardship of natural and artificial freshwater environments: Consequences for biodiversity conservation, Water, 12, 260, https://doi.org/10.3390/w12010260, 2020a.
Cantonati, M., Stevens, L. E., Segadelli, S., Springer, A. E., Goldscheider, N., Celico, F., Filippini, M., Ogata, K., and Gargini, A.: Ecohydrogeology: The interdisciplinary convergence needed to improve the study and stewardship of springs and other groundwater-dependent habitats, biota, and ecosystems, Ecol. Indic., 110, 105803, https://doi.org/10.1016/j.ecolind.2019.105803, 2020b.
Cantonati, M., Segadelli, S., Springer, A. E., Goldscheider, N., Celico, F., Filippini, M., Ogata, K., and Gargini, A.: Geological and hydrochemical prerequisites of unexpectedly high biodiversity in spring ecosystems at the landscape level, Sci. Total Environ., 740, 140157, https://doi.org/10.1016/j.scitotenv.2020.140157, 2020c.
Ceballos, G., Ehrlich, P. R., and Dirzo, R.: Biological annihilation via the ongoing sixth mass extinction signaled by vertebrate population losses and declines, P. Natl. Acad. Sci. USA, 114, E6089–E6096, https://doi.org/10.1073/pnas.1704949114, 2017.
Chadwick, O. A. and Chorover, J.: The chemistry of pedogenic thresholds, Geoderma, 100, 321–353, https://doi.org/10.1016/S0016-7061(01)00027-1, 2001.
Chapelle, F. H.: Geochemistry of Groundwater, in: Treatise on Geochemistry, edited by: Holland, H. D. and Turekian, K. K., Pergamon, 425–449, US Geological Survey, Columbia, SC, USA, https://doi.org/10.1016/B0-08-043751-6/05167-7, 2003.
Chen, Z., Auler, A. S., Bakalowicz, M., Drew, D., Griger, F., Hartmann, J., Jiang, G., Moosdorf, N., Richts, A., Stevanovic, Z., Veni, G., and Goldscheider, N.: The World Karst Aquifer Mapping project: concept, mapping procedure and map of Europe, Hydrogeol. J., 25, 771–785, https://doi.org/10.1007/s10040-016-1519-3, 2017.
Chuman, T., Gürtlerová, P., Hruška, J., and Adamová, M.: Map of geochemical reactivity of rocks of the Czech Republic, Czech Geological Survey, Prague, Czech Republic, 2019.
Chytrý, M., Hennekens, S. M., Jiménez-Alfaro, B., Knollová, I., Dengler, J., Jansen, F., Landucci, F., Schaminée, J. H. J., Adid, S., Agrillo, E., Ambarlı, D., Angelini, P., Apostolova, I., Attorre, F., Berg, C., Bergmeier, E., Biurrun, I., Botta-Dukát, Z., Brisse, H., Campos, J. A., Carlón, L., Čarni, A., Casella, L., Csiky, J., Ćušterevska, R., Dajid Stevanovid, Z., Danihelka, J., De Bie, E., de Ruffray, P., De Sanctis, M., Dickoré, W. B., Dimopoulos, P., Dubyna, D., Dziuba, T., Ejrnæs, R., Ermakov, N., Ewald, J., Fanelli, G., Fernández-González, F., FitzPatrick, Ú., Font, X., GarcíaMijangos, I., Gavilán, R. G., Golub, V., Guarino, R., Haveman, R., Indreica, A., Işık Gürsoy, D., Jandt, U., Janssen, J. A. M., Jiroušek, M., Kącki, Z., Kavgacı, A., Kleikamp, M., Kolomiychuk, V., Krstivojevid Duk, M., Krstonošid, D., Kuzemko, A., Lenoir, J., Lysenko, T., Marcenò, C., Martynenko, V., Michalcová, D., Moeslund, J. E., Onyshchenko, V., Pedashenko, H., Pérez-Haase, A., Peterka, T., Prokhorov, V., Rašomavičius, V., Rodríguez-Rojo, M. P., Rodwell, J. S., Rogova, T., Ruprecht, E., Rūsira, S., Seidler, G., Šibík, J., Šilc, U., Škvorc, Ž., Sopotlieva, D., Stančid, Z., Svenning, J.-C., Swacha, G., Tsiripidis, I., Turtureanu, P. D., Uğurlu, E., Uogintas, D., Valachovič, M., Vashenyak, Y., Vassilev, K., Venanzoni, R., Virtanen, R., Weekes, L., Willner, W., Wohlgemuth, T., and Yamalov, S.: European Vegetation Archive (EVA): an integrated database of European vegetation plots, Appl. Veg. Sci., 19, 173–180, https://doi.org/10.1111/avsc.12191, 2016.
Chytrý, M., Hájek, M., Kočí, M., Pešout, P., Roleček, J., Sádlo, J., Šumberová, K., Sychra, J., Boublík, K., Douda, J., Grulich, V., Härtel, H., Hédl, R., Lustyk, P., Navrátilová, J., Novák, P., Vydrová, P., and Chobot, K.: Red list of habitats of the Czech Republic, Ecol. Indic., 106, 105446, https://doi.org/10.1016/j.ecolind.2019.105446, 2019.
Chytrý, M., Tichý, L., Hennekens, S. M., Knollová, I., Janssen, J. A. M., Rodwell, J. S., Peterka, T., Marcenò, C., Landucci, F., Danihelka, J., Hájek, M., Dengler, J., Novák, P., Zukal, D., Jiménez-Alfaro, B., Mucina, L., Abdulhak, S., Aćić, S., Agrillo, E., Attorre, F., Bergmeier, E., Biurrun, I., Boch, S., Bölöni, J., Bonari, G., Braslavskaya, T., Bruelheide, H., Campos, J. A., Čarni, A., Casella, L., Ćuk, M., Ćušterevska, R., De Bie, E., Delbosc, P., Demina, O., Didukh, Y., Dítě, D., Dziuba, T., Ewald, J., Gavilán, R. G., Gégout, J.-C., Giusso del Galdo, G. P., Golub, V., Goncharova, N., Goral, F., Graf U., Indreica, A., Isermann, M., Jandt, U., Jansen, F., Jansen, J., Jašková, A., Jiroušek, M., Kącki, Z., Kalníková, V., Kavgacı, A., Khanina, L., Korolyuk, A.Yu., Kozhevnikova, M., Kuzemko, A., Küzmič, F., Kuznetsov, O. L., Laiviņš, M., Lavrinenko, I., Lavrinenko, O., Lebedeva, M., Lososová, Z., Lysenko, T., Maciejewski, L., Mardari, C., Marinšek, A., Napreenko, M. G., Onyshchenko, V., Pérez-Haase, A., Pielech, R., Prokhorov, V., Rašomavičius, V., Rodríguez Rojo, M. P., Rūsiņa, S., Schrautzer, J., Šibík, J., Šilc, U., Škvorc, Ž., Smagin, V. A., Stančić, Z., Stanisci, A., Tikhonova, E., Tonteri, T., Uogintas, D., Valachovič, M., Vassilev, K., Vynokurov, D., Willner, W., Yamalov S., Evans, D., Palitzsch Lund, M., Spyropoulou, R., Tryfon, E. and Schaminée J. H. J.: EUNIS Habitat Classification: expert system, characteristic species combinations and distribution maps of European habitats, Appl. Veg. Sci., 23, 1–28, https://doi.org/10.1111/avsc.12519, 2020.
Clymo, R. S.: Ion exchange in Sphagnum and its relation to bog ecology, Ann. Bot.-London, 27, 309–324, https://doi.org/10.1093/oxfordjournals.aob.a083847, 1963.
Ćirić, S., Spasić, Z., Ilić, Z., and Prodanović, D.: Bottling spring water from a Serbian mountain, Pol. J. Environ. Stud., 27, 597–607, https://doi.org/10.15244/pjoes/75816, 2018.
Crossman, J., Bradley, C., Boomer, I., and Milner, A. M.: Water flow dynamics of groundwater-fed streams and their ecological significance in a glacierised catchment, Arct. Antarct. Alp. Res., 43, 364–379, https://doi.org/10.1657/1938-4246-43.3.364, 2011.
Dengler, J., Jansen, F., Glöckler, F., Peet, R. K., De Cáceres, M., Chytrý, M., Ewald, J., Oldeland, J., Lopez-Gonzalez, G., Finckh, M., Mucina, L., Rodwell, J. S., Schaminée, J. H. J., and Spencer, N.: The Global Index of VegetationPlot Databases (GIVD): a new resource for vegetation science, J. Veg. Sci., 22, 582–597, https://doi.org/10.1111/j.1654-1103.2011.01265.x, 2011.
Dierssen, K.: Die wichtigsten Pflanzengesellschaften der Moore NW-Europas, Conservatoire et Jardin botaniques, Genève, 1–382, 1982.
Divíšek, J., Hájek, M., Jamrichová, E., Petr, L., Večeřa, M., Tichý, L., Willner, W., and Horsák, M.: Holocene matters: Landscape history accounts for current species richness of vascular plants in forests and grasslands of eastern Central Europe, J. Biogeogr., 47, 721–735, https://doi.org/10.1111/jbi.13787, 2020.
Duchaufour, R.: Pedology: pedogenesis and classification, Springer, Dordrecht, https://doi.org/10.1007/978-94-011-6003-2, 2012.
Duscher, K., Günther, A., Richts, A., Clos, P., Philipp, U., and Struckmeier, W.: The GIS layers of the “International Hydrogeological Map of Europe 1:1,500,000” in a vector format, Hydrogeol. J., 23, 1867–1875, https://doi.org/10.1007/s10040-015-1296-4, 2015.
Eades, P., Tratt, R., and Shaw, S.: Alkaline Fen and Transition Mire Survey of the North York Moors National Park and Bishop Monkton Ings (report), Natural England, York, 2018.
Evans J. S.: spatialEco, R package version 1.3-4, available at: https://github.com/jeffreyevans/spatialEco, last access: September 2020.
Fairchild, I. J., Bradby, L., Sharp, M., and Tison, J.-L.: Hydrochemistry of carbonate terrains in alpine glacial settings, Earth Surf. Proc. Land., 19, 33–54, https://doi.org/10.1002/esp.3290190104, 1994.
Frei, M., Bielert, U., and Heinrichs, H: Effects of pH, alkalinity and bedrock chemistry on metal concentrations of springs in an acidified catchment (Ecker Dam, Harz Mountains, FRG), Chem. Geol., 170, 221–242, https://doi.org/10.1016/S0009-2541(99)00249-1, 2000.
Gerdol, R., Pontin, A., Tomaselli, M., Bombonato, L., Brancaleoni, L., Gualmini, M., Petraglia, A., Siffi, C., and Gargini A.: Hydrologic controls on water chemistry, vegetation and ecological patterns in two mires in the South-Eastern Alps (Italy), Catena, 86, 86–97, https://doi.org/10.1016/j.catena.2011.02.008, 2011.
Gorham, E.: The chemical composition of some natural waters in the Cairn Gorm-Strath Spey District of Scotland, Limnol. Oceanogr., 2, 143–154, https://doi.org/10.4319/lo.1957.2.2.0143, 1957.
Greenwell, B. M.: pdp: An R Package for Constructing Partial Dependence Plots, R J., 9, 421–436, https://doi.org/10.32614/RJ-2017-016, 2017.
Hájek, M., Hekera, P., and Hájková, P.: Spring fen vegetation and water chemistry in the Western Carpathian flysch zone, Folia Geobot., 37, 205–224, https://doi.org/10.1007/BF02804232, 2002.
Hájek, M., Horsák, M., Hájková, P., and Dítě, D.: Habitat diversity of central European fens in relation to environmental gradients and an effort to standardise fen terminology in ecological studies, Perspect. Plant Ecol., 8, 97–114, https://doi.org/10.1016/j.ppees.2006.08.002, 2006.
Hájek, M., Hájková, P., and Apostolova, I.: New plant associations from Bulgarian mires, Phytologia Balcanica, 14, 377–399, 2008.
Hájek, M., Horsáková, V., Hájková, P., Coufal, R., Dítě, D., Němec, T., and Horsák, M.: Habitat extremity and conservation management stabilise endangered calcareous fens in a changing world, Sci. Total Environ., 719, 134693, https://doi.org/10.1016/j.scitotenv.2019.134693, 2020a.
Hájek, M., Jiménez-Alfaro, B., Hájek, O., Brancaleoni, L., Cantonati, M., Carbognani, M., Dedić A., Dítě, D., Gerdol, R., Hájková, P., Horsáková, V., Jansen, F., Kamberović, J., Kapfer, J., Kolari, T., Lamentowicz, M., Lazarević, P., Mašić, E., Moeslund, J. E., Pérez-Haase, A., Peterka, T., Petraglia, A., Pladevall-Izard, E., Plesková, Z., Segadelli, S., Semeniuk, Y., Singh, P., Šímová, A., Šmerdová, E., Tahvanainen, T., Tomaselli, M., Vystavna Y., Biţă-Nicolae, C., and Horsák, M.: Data from: European map of groundwater pH and calcium, Zenodo, https://doi.org/10.5281/zenodo.4139912, 2020b.
Hájková, P., Hájek, M., and Apostolova, I.: Diversity of wetland vegetation in the Bulgarian high mountains, main gradients and context-dependence of the pH role, Plant Ecol., 184, 111–130, https://doi.org/10.1007/s11258-005-9056-5, 2006.
Hájková, P., Hájek, M., Apostolova, I., Zelený, D., and Dítě, D.: Shifts in the ecological behaviour of plant species between two distant regions: evidence from the base richness gradient in mires, J. Biogeogr., 35, 282–294, https://doi.org/10.1111/j.1365-2699.2007.01793.x, 2008.
Hem, J. D.: Study and interpretation of the chemical characteristics of natural water, U. S. Geological Survey Water-Supply Paper 2254, 1985.
Hengl, T.: GSIF: Global Soil Information Facilities, R package version 0.5-5.1, available at: https://CRAN.R-project.org/package=GSIF, last access: September 2020.
Hengl, T., Heuvelink, G. B. M., and Rossiter, D. G.: About regression-kriging: From equations to case studies, Comput. Geosci., 33, 1301–1315, https://doi.org/10.1016/j.cageo.2007.05.001, 2007.
Hengl, T., Heuvelink, G. B. M., Kempen, B., Leenaars, J. G. B., Walsh, M. G., Shepherd, K. D., Sila, A., MacMillan, R. A., de Jesus, J. M., Tamena, L., and Tondoh, J. E.: Mapping Soil Properties of Africa at 250 m Resolution: Random Forests Significantly Improve Current Predictions, PLOS ONE, 10, e0125814, https://doi.org/10.1371/journal.pone.0125814, 2015.
Hengl, T., de Jesus, J. M., Heuvelink, G. B. M., Ruiperez-Gonzalez, M., Kilibarda, M., Blagotić, A., Shangguan, W., Wright, M. N., Geng, X., Bauer-Marschallinger, B., Guevara, M. A., Vargas, R., MacMillan, R. A., Batjes, N. H., Leenaars, J. G. B., Ribeiro, E., Wheeler, I., Mantel, S., and Kempen, B.: SoilGrids250m: Global gridded soil information based on machine learning, PLOS ONE, 12, e0169748, https://doi.org/10.1371/journal.pone.0169748, 2017.
Hengl, T., Nussbaum, M., Wright, M. N., Heuvelink, G. B. M., and Gräler, B.: Random forest as a generic framework for predictive modeling of spatial and spatio-temporal variables, PeerJ, 6, e5518, https://doi.org/10.7717/peerj.5518, 2018.
Hinterlang, D.: Vegetationsökologie der Weichwasserquellgesellschaften zentraleuropäischer Mittelgebirge, Crunoecia, 1, 1–117, 1992.
Hinterlang, D.: Montio-Cardaminetea: Quell- und Waldsumpf-Gesellschaften, Synopsis der Pflanzengesellschaften Deutschlands, Heft 12, Floristisch-soziologische Arbeitsgemeinschaft e.V., Göttingen, 2017.
Horsáková, V., Hájek, M., Hájková, P., Dítě, D., and Horsák, M.: Principal factors controlling the species richness of European fens differ between habitat specialists and matrix-derived species, Divers. Distrib., 24, 742–754, https://doi.org/10.1111/ddi.12718, 2018.
Janssen, J. A. M., Rodwell, J. S., García-Criado, M., Gubbay, S., Haynes, T., Nieto, A., Sanders, N., Landucci, F., Loidi, J., Ssymank, A., Tahvanainen, T., Valderrabano, M., Acosta, A., Aronsson, M., Arts, G., Attorre, F., Bergmeier, E., Bijlsma, R.-J., Bioret, F., Biţă-Nicolae, C., Biurrun, I., Calix, M., Capelo, J., Čarni, A., Chytrý, M., Dengler, J., Dimopoulos, P., Essl, F., Gardfjell, H., Gigante, D., Giusso del Galdo, G., Hájek, M., Jansen, F., Jansen, J., Kapfer, J., Mickolajczak, A., Molina, J. A., Molnár, Z., Paternoster, D., Piernik, A., Poulin, B., Renaux, B., Schaminée, J. H. J., Šumberová, K., Toivonen, H., Tonteri, T., Tsiripidis, I., Tzonev, R., and Valachovič, M.: European red list of habitats, Part 2, Terrestrial and freshwater habitats, European Commission, European Commission, Luxembourg, https://doi.org/10.2779/091372, 2016.
Jiménez-Alfaro, B., Girardello, M., Chytrý, M., Svenning, J.-C., Willner, W., Gégout, J.-C., Agrillo, E., Campos, J. A., Jandt, U., Kącki, Z., Šilc, U., Slezák, M., Tichý, L., Tsiripidis, I., Turtureanu, P., Ujházyová, M., and Wohlgemuth, T.: History and environment shape species pools and community diversity in European beech forests, Nature Ecology & Evolution, 2, 483–490, https://doi.org/10.1038/s41559-017-0462-6, 2018a.
Jiménez-Alfaro, B., Suárez-Seoane, S., Chytrý, M., Hennekens, S., Willner, W., Hájek, M., Agrillo, E., Álvarez-Martínez, J. M., Bergamini, A., Brisse, H., Brunet, J., Casella, L., Dítě, D., Castell, X., Gillet, F., Hájková, P., Jansen, F., Jandt, U., Kącki, Z., and Tsiripidis, I.: Modelling the distribution and compositional variation of plant communities at the continental scale, Divers. Distrib., 24, 978–990, https://doi.org/10.1111/ddi.12736, 2018b.
Joosten, H., Tanneberger, F., and Moen, A. (eds.): Mires and peatlands of Europe, Status, distribution and conservation, E. Schweizerbart'sche Verlagsbuchhandlung, Stuttgart, Germany, ISBN 978-3-510-65383-6, 2017.
Kadūnas, K., Gedžiūnas, P., Zanevskij, Z., Guobytė, R., Pūtys, P., and Balčiūnaitė, D.: Lietuvos šaltinių katalogas, 220 versmiø ir šaltiniø, Lietuvos Geologijas Tarnyba, Grunto valymo technologijos, Vilnius, 2017.
Kamberović, J., Plenković-Moraj, A., Borojević, K. K., Udovič, M. G., Žutinić, P., Hafner, D., and Cantonati, M.: Algal assemblages in springs of different lithologies (ophiolites vs. limestone) of the Konjuh Mountain (Bosnia and Herzegovina), Acta Bot. Croat., 78, 66–81, https://doi.org/10.2478/botcro-2019-0004, 2019.
Kann, J. and Smith, V. H.: Estimating the probability of exceeding elevated pH values critical to fish populations in a hypereutrophic lake, Can. J. Fish. Aquat. Sci., 56, 2262–2270, 1999.
Kapfer, J., Audorff, V., Beierkuhnlein, C., and Hertel, E.: Do bryophytes show a stronger response than vascular plants to interannual changes in spring water quality?, Freshw. Sci., 31, 625–635, https://doi.org/10.1899/11-037.1, 2012.
Karger, D. N., Conrad, O., Böhner, J., Kawohl, T., Kreft, H., Soria-Auza, R. W., Zimmermann, N. E., Linder, H. P., and Kessler, M.: Climatologies at high resolution for the earth's land surface areas, Sci. Data, 4, 170122, https://doi.org/10.1038/sdata.2017.122, 2017.
Kelmendi, M., Kadriu, S., Sadiku, M., Aliu, M., Sadriu, E., and Hyseni, S. M.: Assessment of drinking water quality of Kopiliq village in Skenderaj, Kosovo, Journal of Water and Land Development, 39, 61–65, https://doi.org/10.2478/jwld-2018-0059, 2018.
Keskin, H. and Grunwald, S.: Regression kriging as a workhorse in the digital soil mapper's toolbox, Geoderma, 326, 22–41, https://doi.org/10.1016/j.geoderma.2018.04.004, 2018.
Kolda, A., Petrić, I., Mucko, M., Gottstein, S., Žutinić, P., Goreta, G., Ternjej, I., Rubinić, J., Radišić, M., and Udovič, M. G.: How environment selects: Resilience and survival of microbial mat community within intermittent karst spring Krčić (Croatia), Ecohydrology, 12, e2063, https://doi.org/10.1002/eco.2063, 2019.
Laburdová, J. and Hájek, M.: Vztah vegetace prameništ' západočeské zřídelní oblasti k chemismu prostředí [Relationships between spring vegetation and environment chemistry in West-Bohemian mineral-spring region], Zprávy České botanické společnosti, 49, 49–71, 2014.
Lajçi, N., Sadiku, M., Lajçi, X., Baruti, B., and Aliu, M.: Assessment of physico-chemical quality of fresh water springs in village Pepaj, Rugova Region, Kosova, Journal of International Environmental Application and Science, 12, 73–81, 2017.
Lamentowicz, M. and Mitchell, E. A.: The ecology of testate amoebae (Protists) in Sphagnum in north-western Poland in relation to peatland ecology, Microb. Ecol., 50, 48–63, https://doi.org/10.1051/limn/09003, 2005.
Lamentowicz, M., Lamentowicz, Ł., van der Knaap, W. O., Gąbka, M., and Mitchell, E. A.: Contrasting species—environment relationships in communities of testate amoebae, bryophytes and vascular plants along the fen–bog gradient, Microb. Ecol., 59, 499–510, https://doi.org/10.1007/s00248-009-9617-6, 2010.
Le, T. D., Kattwinkel, M., Schützenmeister, K., Olson, J. R., Hawkins, C. P., and Schäfer, R. B.: Predicting current and future background ion concentrations in German surface water under climate change, Philos. T. Roy. Soc. B, 374, 20180004, https://doi.org/10.1098/rstb.2018.0004, 2019.
Lewandowski, J., Meinikmann, K., Nützmann, G., and Rosenberry, D. O.: Groundwater—the disregarded component in lake water and nutrient budgets, Part 2: Effects of groundwater on nutrients, Hydrol. Process., 29, 2922–2955, https://doi.org/10.1016/j.jhydrol.2020.124834, 2015.
Malmer, N.: Vegetational gradients in relation to environmental conditions in northwestern European mires, Can. J. Botany, 64, 375–383, https://doi.org/10.1139/b86-054, 1986.
Maxbauer, D. P., Feinberg, J. M., Fox, D. L., and Nater, E. A.: Response of pedogenic magnetite to changing vegetation in soils developed under uniform climate, topography, and parent material, Sci. Rep.-UK, 7, 1–10, https://doi.org/10.1038/s41598-017-17722-2, 2017.
Meng, Q., Liu, Z., and Borders, B. E.: Assessment of regression kriging for spatial interpolation – comparisons of seven GIS interpolation methods, Cartogr. Geogr. Inf. Sc., 40, 28–39, https://doi.org/10.1080/15230406.2013.762138, 2013.
Miles, J.: The pedogenic effects of different species and vegetation types and the implications of succession, J. Soil Sci., 36, 571–584, https://doi.org/10.1111/j.1365-2389.1985.tb00359.x, 1985.
Miller, T. K., Heegaard, E., Hassel, K., and Kapfer, J.: Environmental variables driving species composition in subarctic springs in the face of climate change, J. Veg. Sci., 32, e12955, https://doi.org/10.1111/jvs.12955, 2021.
Mohammed, A. A., Pavlovskii, I., Cey, E. E., and Hayashi, M.: Effects of preferential flow on snowmelt partitioning and groundwater recharge in frozen soils, Hydrol. Earth Syst. Sci., 23, 5017–5031, https://doi.org/10.5194/hess-23-5017-2019, 2019.
Økland, R. H., Økland, T., and Rydgren, K.: A Scandinavian perspective on ecological gradients in north-west European mires: reply to Wheeler and Proctor, J. Ecol., 89, 481–486, https://doi.org/10.1046/j.1365-2745.2001.00573.x, 2001.
Pentecost, A. and Zhaohui, Z.: Bryophytes from some travertine-depositing sites in France and the UK: relationships with climate and water chemistry, J. Bryol., 24, 233–241, https://doi.org/10.1179/037366802125001402, 2002.
Peterka, T., Hájek, M., Jiroušek, M., Jiménez-Alfaro, B., Aunina, L., Bergamini, A., Dítě, D., Felbaba-Klushyna, L., Graf, U., Hájková, P., Hettenbergerová, E., Ivchenko, T. G., Jansen, F., Koroleva, N. E., Lapshina, E. D., Lazarević, P. M., Moen, A., Napreenko, M. G., Pawlikowski, P., Plesková, Z., Sekulová, L., Smagin, V. A., Tahvanainen, T., Thiele, A., Biţa-Nicolae, C., Biurrun, I., Brisse, H., Ćušterevska, R., De Bie, E., Ewald, J., FitzPatrick, Ú., Font, X., Jandt, U., Kącki, Z., Kuzemko, A., Landucci, F., Moeslund, J. E., Pérez-Haase, A., Rašomavičius, V., Rodwell, J. S., Schaminée, J. H., Šilc, U., Stančić, Z., and Chytrý, M.: Formalized classification of European fen vegetation at the alliance level, Appl. Veg. Sci., 20, 124–142, https://doi.org/10.1111/avsc.12271, 2017.
Pham, T. G., Kappas, M., Huynh, C. V., and Nguyen, L. H. K.: Application of Ordinary Kriging and Regression Kriging method for soil properties mapping in hilly region of central Vietnam, ISPRS Int. J. Geo-Inf., 8, 147, https://doi.org/10.3390/ijgi8030147, 2019.
Plesková, Z., Jiroušek, M., Peterka, T., Hájek, T., Dítě, D., Hájková, P., Navrátilová, J., Šímová, A., Syrovátka, V., and Hájek, M.: Testing inter-regional variation in pH niches of fen mosses, J. Veg. Sci., 27, 352–364, https://doi.org/10.1111/jvs.12348, 2016.
R Core Team: R: A language and environment for statistical computing, R Foundation for Statistical Computing, Vienna, Austria, available at: https://www.R-project.org/ (last access: September 2020) (packages=GSIF, spatialEco), 2020.
Ridl, A., Vilenica, M., Ivković, M., Popijač, A., Sivec, I., Miliša, M., and Mihaljević, Z.: Environmental drivers influencing stonefly assemblages along a longitudinal gradient in karst lotic habitats, J. Limnol., 77, 412–427, https://doi.org/10.4081/jlimnol.2018.1816, 2018.
Rydin, H., Jeglum, J. K., and Bennett, K. D.: The biology of peatlands, 2nd Edn., Oxford University Press, https://doi.org/10.1093/acprof:osobl/9780199602995.001.0001, 2013.
Salminen, R., De Vos, W., and Tarvainen, T.: Geochemical atlas of Europe, Geological Survey of Finland, Espoo, 2006.
Savić, A., Dmitrović, D., and Pešić, V.: Ephemeroptera, Plecoptera, and Trichoptera assemblages of karst springs in relation to some environmental factors: a case study in central Bosnia and Herzegovina, Turk. J. Zool., 41, 119–129, https://doi.org/10.3906/zoo-1512-31, 2017.
Schweiger, A. H., Audorff, V., and Beierkuhnlein, C.: The acid taste of climate change: 20th century acidification is re-emerging during a climatic extreme event, Ecosphere, 6, 1–11, https://doi.org/10.1890/ES15-00032.1, 2015.
Segadelli, S., Vescovi, P., Ogata, K., Chelli, A., Zanini, A., Boschetti, T., Petrella, M., Toscani, L., Gargini, A., and Celico, F.: A conceptual hydrogeological model of ophiolitic aquifers (serpentinised peridotite): The test example of Mt. Prinzera (Northern Italy), Hydrol. Process., 32, 969–1201, https://doi.org/10.1002/hyp.11090, 2017.
Sekulová, L., Hájek, M., and Syrovátka, V.: Vegetation–environment relationships in alpine mires of the West Carpathians and the Alps, J. Veg. Sci., 24, 1118–1128, https://doi.org/10.1111/jvs.12035, 2013.
Šímová, A., Pánek, T., Gałka, M., Zernitskaya, V., Hájková, P., Brodská, H., Jamrichová, E., and Hájek, M.: Landslides increased Holocene habitat diversity on a flysch bedrock in the Western Carpathians, Quaternary Sci. Rev., 219, 68–83, https://doi.org/10.1016/j.quascirev.2019.07.009, 2019.
Sjörs, H. and Gunnarsson, U.: Calcium and pH in north and central Swedish mire waters, J. Ecol., 90, 650–657, https://doi.org/10.1046/j.1365-2745.2002.00701.x, 2002.
Song, X. P., Hansen, M. C., Stehman, S. V., Potapov, P. V., Tyukavina, A., Vermote, E. F., and Townshend, J. R.: Global land change from 1982 to 2016, Nature, 560, 639–643, https://doi.org/10.1038/s41586-018-0411-9, 2018.
Soudzilovskaia, N., Cornelissen, J., During, H., Van Logtestijn, R., Lang., S., and Aerts, R.: Similar cation exchange capacities among bryophyte species refute a presumed mechanism of peatland acidification, Ecology, 91, 2716–2726, https://doi.org/10.1890/09-2095.1, 2010.
Soulsby, C., Birkel, C., Geris, J., Dick, J., Tunaley, C., and Tetzlaff, D.: Stream water age distributions controlled by storage dynamics and nonlinear hydrologic connectivity: Modeling with high-resolution isotope data, Water Resour. Res., 51, 7759–7776, https://doi.org/10.1002/2015WR017888, 2015.
Špoljar, M., Štafa, D., Ostojić, A., Dražina, T., Matoničkin Kepčija, R., Kralj Borojević, K., and Primc, B.: Tufa deposition in a karst stream as an indicator of water quality (Papuk Nature Park, Croatia), Ribarstvo, Croatian Journal of Fisheries, UDK:552.545:504.453, 2011.
Stevens, L. E., Schenk, E. R., and Springer, A. E.: Springs ecosystem classification, Ecol. Appl., 31, e2218, https://doi.org/10.1002/eap.2218, 2020.
Szatmári, G. and Pásztor, L.: Comparison of various uncertainty modelling approaches based on geostatistics and machine learning algorithms, Geoderma, 337, 1329–1340, https://doi.org/10.1016/j.geoderma.2018.09.008, 2019.
Tahvanainen, T.: Water chemistry of mires in relation to the poor-rich vegetation gradient and contrasting geochemical zones of the north-eastern Fennoscandian Shield, Folia Geobot., 39, 353–369, https://doi.org/10.1007/BF02803208, 2004.
Tanneberger, F., Bellebaum, J., Dylawerski, M., Fartmann, T., Jurzyk, S., Koska, I., Tegetmeyer, C., and Wojciechowska, M.: Habitats of the globally threatened Aquatic Warbler (Acrocephalus paludicola) in Pomerania – site conditions, flora, and vegetation characteristics, Plant Diversity and Evolution, 129, 253–273, https://doi.org/10.1127/1869-6155/2011/0129-0047, 2011.
Terzić, J., Marković, T., and Reberski, J. L.: Hydrogeological properties of a complex Dinaric karst catchment: Miljacka Spring case study, Environ. Earth Sci., 72, 1129–1142, https://doi.org/10.1007/s12665-013-3031-6, 2014.
Tickner, D., Opperman, J. J., Abell, R., Acreman, M., Arthington, A. H., Bunn, S. E., Cooke, S. J., Dalton, J., Darwall, W., Edwards, G., Harrison, I., Hughes, K., Jones, T., Leclère, D., Lynch, A. J., Leonard, P., McClain, M. E., Muruven, D., Olden, J. D., Ormerod, S. J., Robinson, J., Tharme, R. E., Thieme, M., Tockner, K., Wright, M., and Young, L.: Bending the curve of global freshwater biodiversity loss: an emergency recovery plan, Bioscience, 70, 330–342, https://doi.org/10.1093/biosci/biaa002, 2020.
Udd, D., Mälson, K., Sundberg, S., and Rydin, H.: Explaining species distributions by traits of bryophytes and vascular plants in a patchy landscape, Folia Geobot., 50, 161–174, https://doi.org/10.1007/s12224-015-9219-7, 2015.
Večeřa, M., Divíšek, J., Lenoir, J., Jiménez-Alfaro, B., Biurrun, I., Knollová, I., Agrillo, E., Campos, J. A., Čarni, A., Crespo Jiménez, G., Ćuk, M., Dimopoulos, P., Ewald, J., Fernández-González, F., Gégout, J.-C., Indreica, A., Jandt, U., Jansen, F., Kącki, Z., Rašomavičius, V., Řezníčková, M., Rodwell, J. S., Schaminée, J. H. J., Šilc, U., Svenning, J.-C., Swacha, G., Vassilev, K., Venanzoni, R., Willner, W., Wohlgemuth, T., and Chytrý, M.: Alpha diversity of vascular plants in European forests, J. Biogeogr., 46, 1919–1935, https://doi.org/10.1111/jbi.13624, 2019.
Vicherová, E., Hájek, M., and Hájek, T.: Calcium intolerance of fen mosses: physiological evidence, effects of nutrient availability and successional drivers, Perspect. Plant Ecol., 17, 347–359, https://doi.org/10.1016/j.ppees.2015.06.005, 2015.
Vorren, K. D., Eurola, S., and Tveraabak, U.: The lowland terrestrial mire vegetation about 69∘ N lat. in northern Norway, Tromura, Tromsø Museums Rapportserie, Naturvitenskap, Tromsø Museum, Tromsø, 84, 1999.
Vystavna, Y., Yakovlev, V., Diadin, D., Vergeles, Y., and Stolberg, F.: Hydrochemical characteristics and water quality assessment of surface and ground waters in the transboundary (Russia/Ukraine) Seversky Donets basin, Environ. Earth Sci., 74, 585–596, https://doi.org/10.1007/s12665-015-4060-0, 2015.
Vystavna, Y., Schmidt, S. I., Kopáček, J., Hejzlar, J., Holko, L., Matiatos, I., Wassenaar, L. I., Persoiu, A., Badaluta, C. A., and Huneau, F.: Small-scale chemical and isotopic variability of hydrological pathways in a mountain lake catchment, J. Hydrol., 585, 124834, https://doi.org/10.1016/j.jhydrol.2020.124834, 2020.
Wheeler, B. D. and Proctor, M. C. F.: Ecological gradients, subdivisions and terminology of north-west European mires, J. Ecol., 88, 187–203, https://doi.org/10.1046/j.1365-2745.2000.00455.x, 2000.
White, A. F. and Blum, A. E.: Effects of climate on chemical-weathering in watersheds, Geochim. Cosmochim. Ac., 59, 1729–1747, https://doi.org/10.1016/0016-7037(95)00078-E, 1995.
Wiesmeier, M., Barthold, F., Blank, B., and Kögel-Knabner, I.: Digital mapping of soil organic matter stocks using Random Forest modeling in a semi-arid steppe ecosystem, Plant Soil, 340, 7–24, https://doi.org/10.1007/s11104-010-0425-z, 2011.