the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
Improved estimate of global gross primary production for reproducing its long-term variation, 1982–2017
Yi Zheng
Ruoque Shen
Yawen Wang
Xiangqian Li
Shuguang Liu
Shunlin Liang
Jing M. Chen
Weimin Ju
Li Zhang
Wenping Yuan
Satellite-based models have been widely used to simulate vegetation gross primary production (GPP) at the site, regional, or global scales in recent years. However, accurately reproducing the interannual variations in GPP remains a major challenge, and the long-term changes in GPP remain highly uncertain. In this study, we generated a long-term global GPP dataset at 0.05∘ latitude by 0.05∘ longitude and 8 d interval by revising a light use efficiency model (i.e., EC-LUE model). In the revised EC-LUE model, we integrated the regulations of several major environmental variables: atmospheric CO2 concentration, radiation components, and atmospheric vapor pressure deficit (VPD). These environmental variables showed substantial long-term changes, which could greatly impact the global vegetation productivity. Eddy covariance (EC) measurements at 95 towers from the FLUXNET2015 dataset, covering nine major ecosystem types around the globe, were used to calibrate and validate the model. In general, the revised EC-LUE model could effectively reproduce the spatial, seasonal, and annual variations in the tower-estimated GPP at most sites. The revised EC-LUE model could explain 71 % of the spatial variations in annual GPP over 95 sites. At more than 95 % of the sites, the correlation coefficients (R2) of seasonal changes between tower-estimated and model-simulated GPP are larger than 0.5. Particularly, the revised EC-LUE model improved the model performance in reproducing the interannual variations in GPP, and the averaged R2 between annual mean tower-estimated and model-simulated GPP is 0.44 over all 55 sites with observations longer than 5 years, which is significantly higher than those of the original EC-LUE model (R2=0.36) and other LUE models (R2 ranged from 0.06 to 0.30 with an average value of 0.16). At the global scale, GPP derived from light use efficiency models, machine learning models, and process-based biophysical models shows substantial differences in magnitude and interannual variations. The revised EC-LUE model quantified the mean global GPP from 1982 to 2017 as 106.2±2.9 Pg C yr−1 with the trend 0.15 Pg C yr−1. Sensitivity analysis indicated that GPP simulated by the revised EC-LUE model was sensitive to atmospheric CO2 concentration, VPD, and radiation. Over the period of 1982–2017, the CO2 fertilization effect on the global GPP (0.22±0.07 Pg C yr−1) could be partly offset by increased VPD ( Pg C yr−1). The long-term changes in the environmental variables could be well reflected in global GPP. Overall, the revised EC-LUE model is able to provide a reliable long-term estimate of global GPP. The GPP dataset is available at https://doi.org/10.6084/m9.figshare.8942336.v3 (Zheng et al., 2019).
- Article
(4922 KB) - Full-text XML
-
Supplement
(1090 KB) - BibTeX
- EndNote
Vegetation gross primary production (GPP) is the largest carbon flux component within terrestrial ecosystems and plays an essential role in regulating the global carbon cycle (Canadell et al., 2007; Zhao et al., 2010). As a primary variable of the terrestrial ecosystem cycle, GPP estimates will substantially determine other variables of the carbon cycle (Yuan et al., 2011). Satellite-based GPP models have been developed based on the light use efficiency (LUE) principle (Monteith, 1972; Potter et al., 1993; Running et al., 2004; Xiao et al., 2005; Yuan et al., 2007). Thus far, LUE models have been a major tool for investigating the spatiotemporal changes in GPP and the environmental regulations, either independently or by combining with other ecosystem models (Keenan et al., 2016; Smith et al., 2016).
However, current LUE models exhibit poor performance in reproducing the interannual variations in GPP. A previous study indicated that seven LUE models could only explain 6 %–36 % of the interannual variations in GPP at 51 eddy covariance (EC) towers (Yuan et al., 2014). Similarly, a model comparison showed that none of the examined 16 process-based biophysical models or the three remote sensing products (BESS, MODIS C5, and MODIS C5.1) could consistently reproduce the observed interannual variations in GPP at 11 forest sites in North America (Keenan et al., 2012). Seven LUE models simulated the long-term trends in global GPP that varied from −0.15 to 1.09 Pg C yr−1 over the period 2000–2010 (Cai et al., 2014). An important reason for the poor performance in modeling the interannual variability is that the effect of environmental regulations on vegetation production is not completely integrated into the LUE models (Stocker et al., 2019). In particular, the long-term changes in several environmental variables are very important for accurately simulating the GPP series at the decadal scale.
Several environmental variables should be included in GPP models. Firstly, as we all know, the rising atmospheric CO2 concentration in the past few decades substantially stimulated global vegetation growth (Zhu et al., 2016; Liu et al., 2017). Field experiments using greenhouses or open-top chambers showed that an increase of approximately 300 ppm in CO2 concentration can increase the photosynthesis of C3 plants on the order of 60 % (Norby et al., 1999). Free-air CO2 enrichment (FACE) experiments generally confirmed the enhancement in net primary production (NPP) with the rising CO2 concentration (Ainsworth and Long, 2005). For example, four FACE experiments indicated that the forest NPP consistently increased at the median of 23±2 % when the ambient CO2 concentration was elevated to approximately 550 ppm (Norby et al., 2005). According to observations, the atmospheric CO2 concentration has risen by approximately 20 % from 340 ppm (1982) to 410 ppm (2018) (https://www.esrl.noaa.gov/, last access: 25 June 2019). However, the effects of CO2 fertilization on GPP have not been integrated in most current satellite-based LUE models.
Secondly, solar radiation, or more specifically the photosynthetic active radiation (PAR) substantially influences the vegetation production of the terrestrial ecosystem (Alton et al., 2007; Kanniah et al., 2012; Krupkova et al., 2017). A study indicated that the solar radiation incident at the earth surface underwent significant decadal variations (Wild et al., 2005). A comprehensive analysis based on the datasets of worldwide distributed sites indicated significant decreases in solar radiation (2 % per decade) from the late 1950s to 1990 in the regions of Asia, Europe, North America, and Africa (Gilgen et al., 1998). A later assessment by Wild et al. (2005) showed that the radiation has increased at widespread locations since the mid-1980s.
However, not only the total amount of solar radiation or PAR incident at the earth surface but more importantly also their partitioning into direct and diffuse radiations impact the vegetation productivity (Urban et al., 2007; Kanniah et al., 2012). An increased proportion of diffuse radiation enhances vegetation photosynthesis, because a higher blue ∕ red light ratio within the diffuse radiation may lead to higher light use efficiency (Gu et al., 2002; Alton et al., 2007). For example, the sharply increased diffuse radiation induced by the 1991 Mount Pinatubo eruption enhanced the noontime vegetation productivity of a deciduous forest for the following 2 years (Gu et al., 2003). Besides volcanic aerosols, clouds could also reduce the total and direct radiation, while increasing the proportion of diffuse radiation. Yuan et al. (2010) found that the higher LUE at European forests than North America was because of the higher ratio of cloudy days in Europe. Yuan et al. (2014) further proved that the significantly underestimated GPP during cloudy days by six LUE models was because the effects of diffuse radiation on LUE were neglected in these models.
Thirdly, atmospheric vapor pressure deficit (VPD) is another factor that should be included in GPP models. As an important driver of atmospheric water demand for plants, VPD influences terrestrial ecosystem function and photosynthesis (Rawson et al., 1977; Yuan, et al., 2019). Rising air temperature increases the saturated vapor pressure at a rate of ∼ 7 % K−1 according to the Clausius–Clapeyron relationship, and therefore, VPD will increase if the atmospheric water vapor content does not increase by exactly the same amount as the saturated vapor pressure. Numerous studies indicated significant changes in the relative humidity (ratio of actual water vapor pressure to saturated water vapor pressure) in both humid areas and continental areas located far from oceanic humidity (Van Wijngaarden and Vincent, 2004; Pierce et al., 2013). In particular, the global averaged land surface relative humidity decreased sharply after the late 1990s (Simmons et al., 2010; Willett et al., 2014), and the global averaged land surface VPD increased sharply after the late 1990s (Yuan et al., 2019). The leaf and canopy photosynthetic rate declines when the atmospheric VPD increases due to stomatal closure (Fletcher et al., 2007). A recent study highlighted that increases in VPD rather than changes in precipitation would be a dominant influence on vegetation productivity (Konings et al., 2017). However, currently the influence of long-term VPD variations is not well expressed in many LUE models.
We have developed a LUE model, namely the EC-LUE model, by integrating remote sensing data and eddy covariance data to simulate daily GPP (Yuan et al., 2007, 2010). The model has been evaluated using the observations at EC towers located in Europe, North America, China, and East Asia, covering various ecosystem types (Yuan et al., 2007, 2010; Li et al., 2013). In this study, we revised the EC-LUE model by integrating the impacts of several environmental variables (i.e., atmospheric CO2 concentration, radiation components, and atmospheric VPD) across a long-term temporal scale. Firstly, we evaluated the effectiveness of the revised EC-LUE model in determining the spatial, seasonal, and interannual variations in GPP from multiple eddy covariance sites. Secondly, a global GPP dataset at 0.05∘ spatial resolution was generated based on the optimized model. Finally, we analyzed the contributions of the aforementioned environmental variables to the global GPP and discussed the spatial and interannual variations in GPP from different datasets.
2.1 Data from the eddy covariance towers
The FLUXNET2015 dataset (http://www.fluxdata.org, last access: 2 March 2018) includes over 200 variables of carbon fluxes, energy fluxes, and meteorological variables collected and processed at sites by the FLUXNET community. In our study, 95 EC sites in the FLUXNET2015 dataset were utilized to optimize the parameters and evaluate the performance of the revised EC-LUE model, including nine major terrestrial ecosystem vegetation types (Table 1): evergreen broadleaf forest (EBF), evergreen needleleaf forest (ENF), deciduous broadleaf forest (DBF), mixed forest (MF), grassland (GRA), savanna (SAV), shrubland (SHR), wetland (WET), and cropland (CRO). More information about the characteristics of these sites can be found at the FLUXNET website. For each site, the daily GPP, PAR, air temperature (Ta), and VPD were used in our study. The GPP variable (GPP_NT_ VUT_REF) used in this study was estimated from the nighttime partitioning method. The corresponding net ecosystem exchange (NEE) was generated using the variable friction velocity (USTAR) threshold for each year (VUT), in which 40 versions of NEE were created by using different percentiles of USTAR thresholds. The model efficiency between each version and the other 39 versions was calculated to test their similarities, and the reference (REF) NEE was selected as the one with the higher model efficiency sum (the most similar to the other 39). The 120 daily meteorological variables were gap-filled or downscaled from the ERA-Interim reanalysis dataset in both space and time (Vuichard and Papale, 2015). The gap-filling technique of the carbon flux measurements and meteorological variables is the marginal distribution sampling (MDS) method described in Reichstein et al. (2005). In the FLUXNET 2015 dataset, the quality flags ranged from 0 to 1 to indicate percentage of measured and good-quality gap-filled data. For each variable, we used the daily/monthly values with more than 80 % of good-quality data (quality flag > 0.8). We aggregated the daily values to an 8 d time step. And only the 8 d measurements with more than 5 d valid values were used.
2.2 Data at the global scale
The global-scale datasets used in this study are shown in Table 2. The meteorological reanalysis dataset was derived from the second Modern-Era Retrospective analysis for Research and Applications (MERRA-2) dataset. It was produced by NASA's Global Modeling and Assimilation Office that used an upgraded version of GEOS-5 (Rienecker et al., 2011). It has been validated carefully using surface meteorological datasets and an enhanced assimilation system to reduce the uncertainty in various meteorological variables globally. In our study, we obtained the daily mean air temperature (Ta, ∘C), mean dew point temperature (Td, ∘C), total direct PAR (PARdr, MJ m−2 d−1), and total diffuse PAR (PARdf, MJ m−2 d−1) at 0.625∘ in longitude by 0.5∘ in latitude from 1982 to 2017. VPD was calculated from air temperature and dew point temperature:
where SVP is the saturated vapor pressure (kPa), and RH is the relative humidity. We aggregated the daily variables (air temperature, dew point temperature, VPD, direct PAR, and diffuse PAR) to 8 d interval temporal resolution. And these variables were resampled to the spatial resolution of 0.05∘ latitude by 0.05∘ longitude using the bilinear interpolation method.
The 8 d Global LAnd Surface Satellite Leaf Area Index (GLASS LAI) dataset at 0.05∘ latitude by 0.05∘ longitude was adopted to indicate vegetation growth from 1982 to 2017. It was produced using the general regression neural networks (GRNNs) trained with the fused MOD15 LAI and CYCLOPES LAI and the preprocessed MODIS and AVHRR reflectance data over the BELMANIP sites (Xiao et al., 2016). Product validation and comparison showed that the GLASS LAI product was spatially complete and temporally continuous with lower uncertainty (Xu et al., 2018).
Additionally, the MCD12Q1 product with the IGBP classification scheme was used as the input land cover map. The ISLSCP II C4 vegetation percentage map was used to separate the C3 and C4 crop. The NOAA Earth System Research Laboratory (ESRL) CO2 concentration dataset was used to express the CO2 fertilization effect.
2.3 The revised EC-LUE model
The terrestrial vegetation GPP can be expressed as follows in the revised EC-LUE model:
where εmsu is the maximum LUE of sunlit leaves; APARsu is the PAR absorbed by sunlit leaves; εmsh is the maximum LUE of shaded leaves; APARsh is the PAR absorbed by shaded leaves; and Cs, Ts, and Ws represent the downward regulation scalars of atmospheric CO2 concentration ([CO2]), air temperature, and VPD on LUE ranging from 0 to 1; min represents the minimum value.
The effect of atmospheric CO2 concentration on GPP is determined by the following equations (Farquhar et al., 1980; Collatz et al., 1991):
where φ is the CO2 compensation point in the absence of dark respiration (ppm), Ci is the leaf internal CO2 concentration, Ca is the atmospheric CO2 concentration, and χ is the ratio of leaf internal to atmospheric CO2 concentration which can be estimated as follows (Prentice et al., 2014; Keenan et al., 2016):
where ε is a parameter related to the “carbon cost of water”, which means the sensitivity of VPD to χ; K is the Michaelis–Menten coefficient of Rubisco; and η* is the viscosity of water relative to its value at 25 ∘C (Korson et al., 1969).
where Po is the partial pressure of O2, and Kc and Ko are the Michaelis–Menten constants for CO2 and O2 (Keenan et al., 2016):
where Ta is air temperature (unit: K) and R is the molar gas constant (8.314 J mol−1 K−1).
Table 3Optimized parameters (εmsu, εmsh, φ, and VPD0) of the revised EC-LUE model for different vegetation types.

Ts and Ws can be expressed as follows:
where Tmin, Topt, and Tmax are the minimum, optimum, and maximum temperatures for vegetation photosynthesis, respectively (Yuan et al., 2007); VPD0 is the half-saturation coefficient of the VPD constraint equation (k Pa).
APARsu and APARsh can be expressed as follows (Chen et al., 1999):
where PARdir is the direct PAR; PARdif is the diffuse PAR; PARdif,u is the diffuse PAR under the canopy; C represents the multiple scattering effects of direct radiation; Ω is the clumping index, which is set according to vegetation types (Tang et al., 2007); θ is the solar zenith angle; β is the mean leaf–sun angle, which is set to 60∘; and is the representative zenith angle for diffuse radiation transmission and can be expressed by LAI (Chen et al., 1999):
The LAIs of shaded leaves (LAIsh) and sunlit leaves (LAIsu) in Eqs. (14) and (15) are computed following Chen et al. (1999):
2.4 Model calibration and validation
Cross-validation method was used to calibrate and validate the revised EC-LUE model. About 50 % of the sites were randomly selected to calibrate model parameters for each vegetation type, and the remaining 50 % of the sites were used to validate the model. This parameterization process was repeated until all possible combinations of 50 % sites were achieved for each vegetation type. The nonlinear regression procedure (Proc NLIN) in the Statistical Analysis System (SAS, SAS Institute Inc., Cary, NC, USA) was applied to optimize the model parameters (εmsu, εmsh, φ, and VPD0) using 8 d estimated GPP based on EC measurements. The mean GPP simulations of 8 d from all validation runs only were used to model validation. At the global scale, mean calibrated parameter values (Table 3) were used to produce a GPP dataset at spatial resolution and 8 d temporal resolution over 1982–2017. In order to investigate the uncertainties of the global GPP dataset, 10 000 sets of optimized parameters were randomly selected to simulate global GPP by assuming a normal distribution of these parameters (Table 3). The uncertainty of global GPP simulations was determined by the mean absolute deviation (MAD) of all the 10 000 simulations (Khair et al., 2017).
Three metrics, the coefficient of determination (R2), RMSE, and bias (the difference between observations and simulations) were adopted to evaluate the performance of the revised EC-LUE model. Additionally, Kendall's coefficient of rank correlation τ (Kanji, 1999) was used to quantify the agreement of seasonal changes between the simulated and tower-estimated GPP. The Kendall coefficient measured the tendency coherence between predicted and observed GPP by comparing the ranks assigned to successive pairs. If and have the same sign (positive or negative), the pair would be concordant, or discordant. With time series data with n observations, the Kendall coefficient of rank correlation τ can be expressed as
where is the total combination of pairs, C is the number of concordant pairs, and D is the number of discordant pairs. Kendall's coefficient ranged from −1 (C=0) to 1 (D=0). The Kendall coefficient is much closer to 1, which means a stronger positive relationship between the seasonal patterns of the simulated and tower-estimated GPP.
In addition, we compared the model performance of the revised EC-LUE model with seven light use efficiency models, three machine learning methods, and 10 process-based biophysical models at a monthly step. The participating light use efficiency models include CASA (Potter et al., 1993), CFlux (Turner et al., 2006; King et al., 2011), CFix (Veroustraete et al., 2002), MODIS (Running et al., 2004), VPM (Xiao et al., 2005), VPRM (Mahadevan et al., 2008), and EC-LUE (Yuan et al., 2007). We calibrated the model parameters of all seven light use efficiency models based on the eddy covariance measurements using the same parameterization method as the revised EC-LUE model (see the above method), and then we compared the GPP simulations of seven LUE models driven by EC tower-based meteorology data against the estimated GPP based on EC measurements. For the comparison with machine learning models and process-based biophysical models, we collected their global monthly GPP products released by FLUXCOM (Jung et al., 2017) and the TRENDY program (version 5) (Le Quéré et al., 2016), respectively. The FLUXCOM program uses the artificial neural network method (FLUXCOM ANN), the multivariate adaptive regression splines method (FLUXCOM MARS), and the random forest method (FLUXCOM RF). The TRENDY program includes the CSIRO Atmosphere and Biosphere Land Exchange (CABLE) (Zhang et al., 2013), the coupled Canadian Land Surface Scheme and Canadian Terrestrial Ecosystem Model (CLASS-CTEM) (Melton and Arora, 2016), the Community Land Model (CLM) (Oleson et al., 2013), the Integrated Science Assessment Model (ISAM) (Jain et al., 2013), the land component of the Max Planck Institute Earth System Model (JSBACH) (Reick et al., 2013), the Joint UK Land Environment Simulator (JULES) (Clark et al., 2011), the Lund-Postdam-Jena General Ecosystem Simulator (LPJ-GUESS) (Smith et al., 2014), the Land surface Processes and eXchanges (LPX-Bern) (Stocker et al., 2014), the ORganizing Carbon and Hydrology In Dynamic EcosystEms (ORCHIDEE) (Krinner et al., 2005), and the Vegetation Integrated Simulator for Trace Gases (VISIT) (Kato et al., 2013). The monthly GPP simulations at all investigated EC sites were derived from their global products, and equally we obtained the monthly GPP simulations of the revised EC-LUE model from its global dataset driven by the MERRA-2 reanalysis dataset.
2.5 Environmental contributions to long-term changes in GPP
To evaluate the contribution of the major environmental variables to GPP, including the atmospheric CO2 concentration ([CO2]), climate, and satellite-based LAI, two types of experimental simulations were performed. The first simulation experiment (SALL) was a normal model run, with all the environmental drivers changing over time. In the second type of simulation experiments (SCLI0, SLAI0, and ), two driving factors could be varied with time while maintaining the third constant at an initial baseline level. For example, the SCLI0 simulation experiment allowed the LAI and atmospheric [CO2] to vary with time while the climate variables were kept constant at 1982 values. The SLAI0 () simulation experiments kept LAI (atmospheric [CO2]) constant at 1982 values and varied the other two variables.
Considering the differences between the simulation results of the first type (SALL) and the second type ( and SLAI0) of experiments, the GPP sensitivities to atmospheric [CO2] () and LAI (βLAI) were estimated as follows:
where ΔGPPi, ΔCO2i, and ΔLAIi denote the differences in the GPP simulations, atmospheric [CO2], and LAI between the two model experiments from 1982 to 2017, and ε is the stochastic error term.
The GPP sensitivities to the three climate variables air temperature (), VPD (βVPD), and PAR (βPAR) were calculated using a multiple regression approach:
where , ΔVPDi, and ΔPARi denote the differences in Ta, VPD, and PAR time series between the two model experiments (SALL and SCLI0), respectively. The regression coefficient β was estimated using the maximum likelihood analysis.
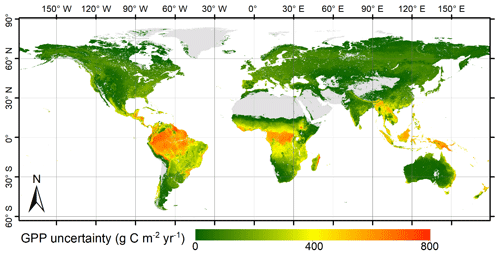
Figure 1Comparisons between annual mean GPP estimated from EC towers and annual mean GPP simulated by the revised EC-LUE model. The modeled GPP values were simulated using (a) tower-derived meteorology and (b) global reanalysis meteorology. The black lines are the regression lines, and the red dashed lines are the 1 : 1 lines. The equations at the bottom of each panel are the regression equations derived from all the sites.
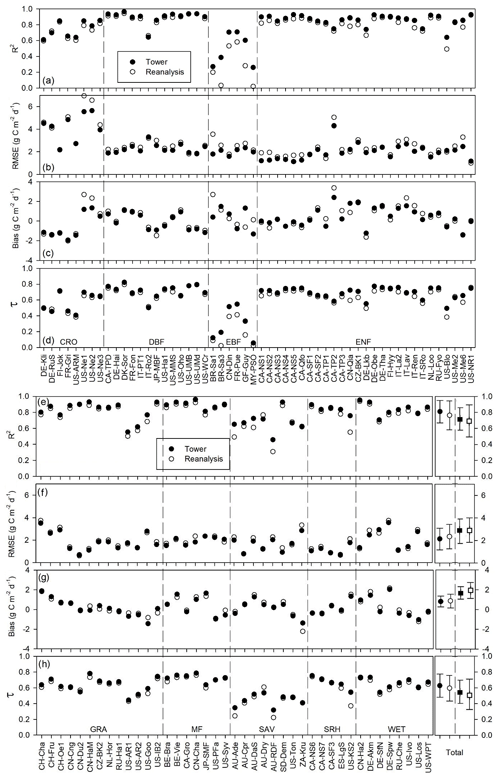
Figure 2Comparisons of 8 d mean GPP between the model-simulated GPP and tower-estimated GPP. Solid and open dots indicate the GPP simulations of the revised EC-LUE model derived from the tower-derived meteorology data and the meteorological reanalysis dataset, respectively; solid and open squares indicate the GPP simulations of the original EC-LUE model derived from the tower-derived meteorology data and the meteorological reanalysis dataset, respectively.
3.1 Model performance
In general, the revised EC-LUE model could effectively reproduce the spatial, seasonal, and annual variations in the tower-estimated GPP at most sites (Figs. 1–3). The revised EC-LUE model explained 71 % and 64 % of the spatial variations in GPP across all the validation sites by using the tower-derived meteorology data and the meteorological reanalysis dataset, respectively (Fig. 1).
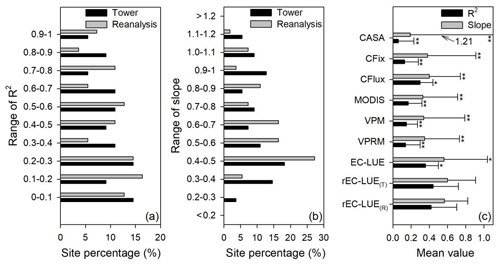
Figure 3Site percentage of (a) correlation coefficients (R2) and (b) regression slopes between the model-simulated and tower-based interannual variabilities in GPP. (c) Averaged values (error bars represent the standard deviations) of R2 and slope for various LUE models. rEC-LUE(T) and rEC-LUE(R) indicate the revised EC-LUE models derived from the tower-derived meteorology data and the meteorological reanalysis dataset. The R2 and slopes of the other seven LUE models (i.e., EC-LUE, VPRM, VPM, MODIS, CFlux, CFix, and CASA) in the figure were obtained from the study by Yuan et al. (2014). and * indicate a significant difference in statistic variables (R2 and slope) between the rEC-LUE(T) and other LUE models (i.e., rEC-LUE(T) and other seven LUE models) at p value < 0.01 and p value < 0.05, respectively.
The revised EC-LUE model also showed a good performance in reproducing the seasonal variations in GPP at most EC sites (Fig. 2). In this study, we compared the modeled and tower GPP at an 8 d step for each site to examine the model capacity in reproducing the temporal variations in GPP. In terms of GPP simulations driven by tower-derived meteorology data, the coefficients of determination (R2) varied from 0.26 at the MY-PSO site to 0.96 at the DK-Sor site, with most of them being statistically significant (p value < 0.05) (Fig. 2a, e), and the mean R2 was 0.81 over all investigated sites. The low R2 values (< 0.4) were found at three tropical forest sites (i.e., MY-PSO, BR-Sa1, and BR-Sa3). The averaged Kendall correlation coefficient (τ) was 0.63 over all sites, indicating a strong seasonal coherence between simulated and tower-estimated GPP (Fig. 2d, h). Similarly, τ at tropical forest sites was generally lower than at other sites. According to the RMSE and absolute value of bias, the revised EC-LUE model performed very well at most sites. The averaged RMSE and absolute value of bias over all the sites were 2.13 and 0.81 g C m−2 d−1, respectively (Fig. 2b–c, f–g). In addition, there was no obvious difference between the seasonal GPP performances using the tower-derived meteorology data and the meteorological reanalysis dataset (Fig. 2). On average, the revised EC-LUE model showed higher R2 and τ and lower RMSE and absolute value of bias than the original EC-LUE model (Fig. 2). Furthermore, we selected three sites with high R2 (US-UMB; DBF; R2=0.93), median R2 (CN-Din; EBF; R2=0.71), and low R2 (Br-Sa3; EBF; R2=0.39) to illustrate the time series changes of observed and simulated GPP, LAI, and environmental factors (i.e., air temperature, VPD, and PAR) (Figs. S1–S3). At the US-UMB site, the model captured the GPP variations well year round with no obvious bias (Fig. S1). At the CN-Din site, the model generally performed well except for the underestimation at the end of the year (November–December) with decreased LAI (Fig. S2). However, at the Br-Sa3 site, the model could not capture the variations in GPP for the vegetation greenness and environmental factors varying slightly during the year (Fig. S3).
The ability of the LUE models to reproduce the interannual variations in GPP was investigated at 55 EC towers with observations greater than 5 years (Table 1; Fig. 3). We examined the relations between the mean annual GPP simulations and observations at each site and used the coefficient correlation (R2) and slope of the regression relationship to investigate the model capability of simulating the interannual variations in GPP. The result showed that the revised EC-LUE model could effectively determine the interannual variations in GPP (Fig. 3). Approximately 42 % and 40 % of the sites showed higher R2 values (> 0.5) by using the tower-derived meteorology data and the meteorological reanalysis dataset (Fig. 3a). The averaged R2 for the revised EC-LUE model was 0.44 by using the tower-derived meteorology data, which was significantly higher than the original EC-LUE model (R2=0.36) and other LUE models (R2 ranged from 0.06 to 0.30 with an average value of 0.16) (Fig. 3c). The averaged R2 for the revised EC-LUE model was 0.42 by using the meteorological reanalysis dataset. The averaged slopes of the revised EC-LUE model were 0.60 and 0.57 by using the tower-derived meteorology data and the meteorological reanalysis dataset (Fig. 3c).
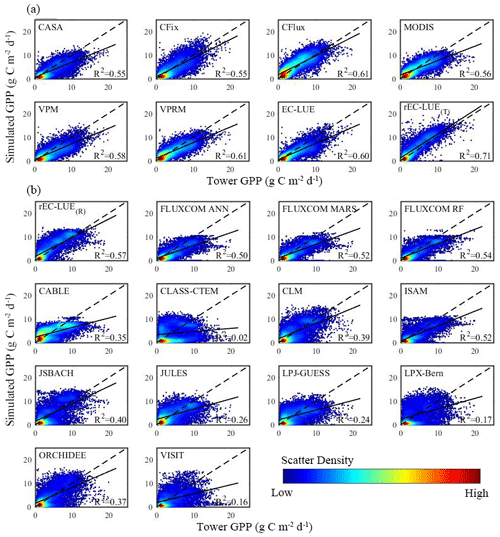
Figure 4Comparisons between estimated GPP based on EC measurements and GPP simulations in growing season (defined as temperature larger than 0∘) by the various models (including LUE models, machine learning models, and process-based biophysical models in TRENDY) at a monthly scale. The comparison of GPP simulations was simulated using (a) tower-derived meteorology data and (b) global reanalysis meteorology data, respectively (see Sect. 2.4). rEC-LUE(T) and rEC-LUE(R) indicate the simulations of the revised EC-LUE model derived from tower-derived meteorology data and global reanalysis meteorology data, respectively.
Additionally, we examined the model performance of the revised EC-LUE model, other LUE models, machine learning models, and process-based biophysical models in TRENDY at a monthly step by comparing against EC tower-estimated GPP (Fig. 4). In comparison with seven LUE models driven by the EC tower-based meteorology dataset, the overall R2 of the revised EC-LUE model was 0.71, higher than the original EC-LUE model and other LUE models (R2 ranged from 0.55 to 0.61) (Fig. 4a). For each site, we compared the R2, RMSE, and absolute value of bias of the individual model with the averaged value of all eight LUE models (each site has an averaged R2, RMSE, and absolute value of bias) (Fig. S4a1–c1). The revised EC-LUE model had higher R2 than the mean R2 of the eight LUE models at 62 % of sites, which was comparable with the original EC-LUE model (63 % of sites) and VPM model (60 % of sites) (Fig. S4a1). Moreover, the revised EC-LUE model showed the lower RMSE and absolute value of bias compared to mean values of all eight LUE models at 68 % and 67 % of sites, respectively, which indicated the better performance compared to the other LUE models at most sites (Fig. S4b1–c1). By using the global reanalysis meteorology data, we compared the performance of the revised EC-LUE model with three existing machine learning model products and 10 process-based biophysical model products in TRENDY (Fig. 4b). The overall R2 of the revised EC-LUE model (R2=0.57) was higher than that of other models (R2 ranged from 0.02 to 0.54) (Fig. 4b). The revised EC-LUE model, FLUXCOM ANN, and FLUXCOM MARS had more sites (over 90 %) with higher R2 than the mean R2 (Fig. S4a2). And the revised EC-LUE model, FLUXCOM MARS, and FLUXCOM RF showed the lower RMSE at more than 90 % of sites (Fig. S4b2). Compared to the other models, the revised EC-LUE model had the highest site percentage (81 %) with a lower absolute value of bias (Fig. S4c2). Furthermore, the revised EC-LUE model had a higher R2, higher τ, lower RMSE, and lower absolute value of bias at most of the sites (Fig. S5).

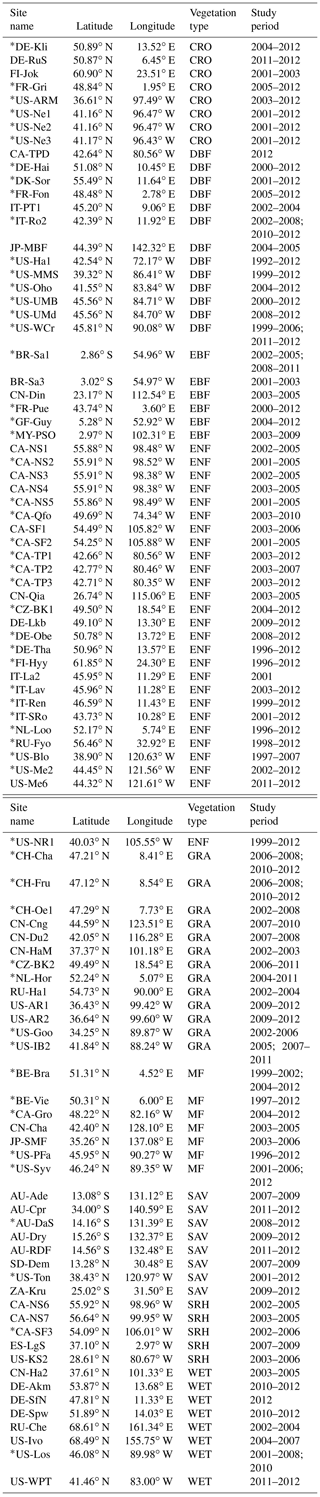
Figure 5Spatial pattern of global GPP simulated by the revised EC-LUE model during 1982–2017: (a) averaged annual GPP; (b) averaged annual GPP at different temperature and precipitation gradients.
3.2 Spatial–temporal patterns of global GPP
A global GPP dataset at 0.05∘ latitude by 0.05∘ longitude and an 8 d interval was generated from 1982 to 2017 based on the revised EC-LUE model. The global GPP was 106.2±2.9 Pg C yr−1 across the vegetated area averaged from 1982 to 2017. The GPP was high over the tropical forest areas, such as the Amazon and Southeast Asia, where the moisture and temperature conditions are sufficient for photosynthesis (Fig. 5a). The GPP decreased with the decreasing gradients of temperature and precipitation (Fig. 5b). The moderate GPP was found in temperate and subhumid regions, and the lowest GPP was located in arid or cold regions, where either precipitation or temperature is limited (Fig. 5b).
The long-term trend of GPP over the period of 1982–2017 was determined using a linear regression analysis (Fig. 6). In general, the revised EC-LUE model showed an increased trend in the annual mean GPP from 1982 to 2017. Approximately 69.5 % of the vegetated areas, mainly located in temperate and humid regions, showed increased trends. The spatial pattern of the GPP trend along with the temperature and precipitation gradients was substantially heterogeneous (Fig. 6b). The decreased GPP was found in the tropic regions, especially in the Amazon forest (Fig. 6a). The extremely cold or arid areas exhibited fewer variations in GPP (Fig. 6b).
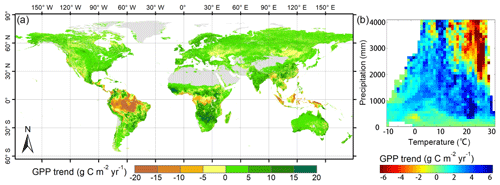
In addition, this study used the MAD of 10 000 simulations to quantify the uncertainty of estimated GPP globally (see methods). Over the globe, the mean uncertainty of estimated GPP by the revised EC-LUE model is 19.33 Pg C yr−1. The GPP uncertainties were found to be low in high and middle latitudes but relatively high in tropical forests (about 600 g C m−2 yr−1) (Fig. 7).
3.3 Contributions of environmental variables to GPP
To quantify the contributions of the environmental variables to long-term changes in GPP, we explored the sensitivity of global summed GPP to climate variables (i.e., VPD, Ta, and PAR), LAI, and atmospheric CO2 (Fig. 8). The global summed GPP generated from different experimental simulations (Sect. 2.5) appeared differently in terms of the annual mean value, trend, and standard deviation (Fig. 8a). The normal simulated GPP (SALL GPP, all the environmental drivers changing over time) significantly increased at the rate of 0.15 Pg C yr−1, while the increasing rate of SCLI0 GPP (climate variables were kept constant at 1982 values) was even greater (0.41 Pg C yr−1). On the contrary, the SLAI0 GPP (LAI was kept constant at 1982 values) and the GPP (atmospheric [CO2] was kept constant at 1982 values) showed an insignificantly decreasing trend at the rate of −0.04 and −0.07 Pg C yr−1 (Fig. 8a). The GPP sensitivity analysis showed that the global GPP decreased by 6.67±5.04 Pg C with a 0.1 kPa increase in VPD, which was comparable to the increase in GPP with 0.1 unit greening of LAI (i.e., Pg C 0.1 unit−1) or a 100 MJ increase in PAR (i.e., Pg C 100 MJ−1) (Fig. 8b). The global GPP increased by 12.31±0.61 Pg C with a 100 ppm−1 rise of atmospheric [CO2] (i.e., Pg C 100 ppm−1). Over the period of 1982–2017, the increased VPD resulted in global GPP decreases of Pg C yr−1, which could partly counteract the fertilization effect of CO2 (0.22±0.07 Pg C yr−1). The global GPP showed a decreasing trend after 2001 due to the joint effect of increased VPD and decreased PAR (Fig. 8c). While the increasing trend of GPP before 2000 was affected by the rising atmospheric [CO2], greening of LAI, and increased PAR (Fig. 8c).
4.1 Model accuracy analysis
Numerous studies have shown that most GPP models can reproduce the spatial changes in GPP but failed to reproduce the temporal variations (Keenan et al., 2012; Yuan et al., 2014). Therefore, the capacity to reproduce realistic interannual variations for a GPP model is significantly important. In our study, the revised EC-LUE model performed a higher accuracy in reproducing the interannual variations in GPP than did the original EC-LUE model and other LUE models. Yuan et al. (2014) reported that the averaged slope of the regression relation between the mean annual GPP simulated by seven LUE models and the mean annual GPP estimated from the EC towers ranged from 0.19 to 0.56 (Fig. 3c). In contrast, the revised EC-LUE model showed a higher slope of regression relation (0.60), which is much closer to 1 than that obtained from other LUE models (Fig. 3c). The VPM GPP showed fewer interannual variations across most biomes (R2<0.5), probably because of the insensitivity of the environmental stress factors at the interannual scale (Zhang et al., 2017). In contrast, 42 % of the sites showed higher R2 values (> 0.5) for the revised EC-LUE model. The improvements of the revised EC-LUE model in reproducing interannual variations are owing to the integration of several important environmental drivers for vegetation production (i.e., atmospheric CO2 concentration, radiation components, and VPD), which exhibited large variations and contributed significantly to vegetation production at an interannual scale.
By integrating the atmospheric CO2 concentration, the revised EC-LUE model suggested a CO2 sensitivity () of 12.31±0.61 Pg C per 100 ppm (Fig. 8b), which indicates an increase of 11.6 % in GPP with a rise of 100 ppm in atmospheric [CO2]. Our estimate is comparable to the observed response of NPP to the increased CO2 in the FACE experiments (13 % per 100 ppm) and estimates of other ecosystem models (5 %–20 % per 100 ppm) (Piao et al., 2013). The elevated atmospheric CO2 concentration substantially contributes to vegetation productivity.
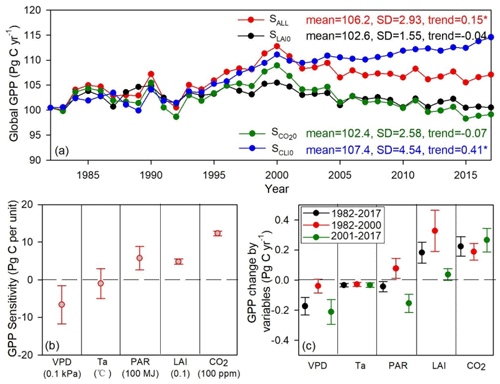
Figure 8Long-term changes in global GPP and the environmental regulations: (a) global summed GPP derived from the four experimental simulations in Sect. 2.5; (b) GPP sensitivity to climate variables (i.e., VPD, Ta, and PAR), LAI, and atmospheric CO2; (c) contributions of climate variables (i.e., VPD, Ta, and PAR), LAI, and atmospheric CO2 to GPP changes over 1982–2017, 1982–2000, and 2001–2017. The asterisk indicates the significant level at p value < 0.05.
The evaporation fraction (EF), namely the ratio of evapotranspiration (ET) to net radiation (Rn), was used to indicate the water stress on vegetation growth in the original EC-LUE model (Yuan et al., 2007, 2010). The atmospheric VPD was used to indicate water stress to avoid the aggregated errors from ET simulations in the revised EC-LUE model. Physiologically, vegetation production is sensitive to both atmospheric VPD and soil moisture availability to roots. Several studies have reported highly consistent interannual variability of VPD and soil moisture (Zhou et al., 2019a, b). In addition, recent studies highlighted that the increase in VPD had a larger limitation to the surface conductance and evapotranspiration than soil moisture over short timescales in many biomes (Novick et al., 2016; Sulman et al., 2016). Other studies have also suggested substantial impacts of VPD on vegetation growth (de Cárcer et al., 2018; Ding et al., 2018), forest mortality (Williams et al., 2013), and crop yields (Lobell et al., 2014). It is increasingly important to integrate the atmospheric water constraint into carbon and water flux modeling.
4.2 Comparison of global GPP products
Global and regional GPP estimates remain highly uncertain despite the substantial advances in remote sensing technology, ground observations, and theory of carbon flux modeling (Zheng et al., 2018; Ryu et al., 2019). At a regional scale, we compared the annual mean GPP between the revised EC-LUE model and other models across the bioclimatic zones in the Köppen–Geiger climate classification map (Beck et al., 2018) (Fig. 9). The GPP of the revised EC-LUE model was comparable to the mean value of other models for each bioclimatic zone (Fig. 9a). The GPP of different models exhibited large discrepancies in tropical regions (Af, Am, Aw) (Fig. 9a). The correlations (R2) of GPP across all the bioclimatic zones between the revised EC-LUE model and other models ranged from 0.73 (LPX-Bern) to 0.95 (FLUXCOM MARS, FLUXCOM RF) (Fig. 9b).
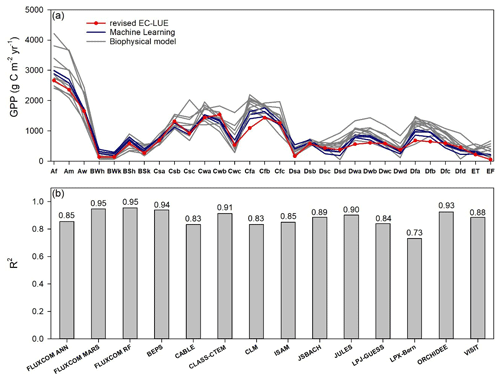
Figure 9Comparisons of long-term (1982 to 2010s) averaged GPP between the revised EC-LUE model and other models across bioclimatic zones in the Köppen–Geiger climate classification map (Beck et al., 2018). (a) The regional averaged value (b) correlation coefficients (R2) of GPP across all the bioclimatic zones between the revised EC-LUE model and other models. These models include three machine learning models (FLUXCOM ANN, FLUXCOM MARS, FLUXCOM RF; Jung et al., 2017), the biophysical model BEPS (Ju et al., 2006; Liu et al., 2018), and 10 biophysical models in TRENDY (CABLE, CLASS-CTEM, CLM, ISAM, JSBACH, JULES, LPJ-GUESS, LPX-Bern, ORCHIDEE, and VISIT). The abbreviations for the bioclimatic zones are as follows: Af, tropical, rainforest; Am, tropical, monsoon; Aw, tropical, savannah; BWh, arid, desert, hot; BWk, arid, desert, cold; BSh, arid, steppe, hot; BSk, arid, steppe, cold; Csa, temperate, dry summer, hot summer; Csb, temperate, dry summer, warm summer; Csc, temperate, dry summer, cold summer; Cwa, temperate, dry winter, hot summer; Cwb, temperate, dry winter, warm summer; Cwc, temperate, dry winter, cold summer; Cfa, temperate, no dry season, hot summer; Cfb temperate, no dry season, warm summer; Cfc, temperate, no dry season, cold summer; Dsa, cold, dry summer, hot summer; Dsb, cold, dry summer, warm summer; Dsc, cold, dry summer, cold summer; Dsd, cold, dry summer, very cold winter; Dwa, cold, dry winter, hot summer; Dwb, cold, dry winter, warm summer; Dwc, cold, dry winter, cold summer; Dwd, cold, dry winter, very cold winter; Dfa, cold, no dry season, hot summer; Dfb, cold, no dry season, warm summer; Dfc, cold, no dry season, cold summer; Dfd, cold, no dry season, very cold winter; ET, polar, tundra; EF, polar, frost.
At a global scale, our study showed large differences in the magnitude of global GPP estimated by various models varied from 92.7 to 168.7 Pg C yr−1 (Figs. 10–11). The LUE models simulated the global GPP to range from 92.7 to 133.7 Pg C yr−1 (Fig. 11a1). Several machine learning approaches estimated the global GPP to range from 111.0 to 144.2 Pg C yr−1 (Fig. 11a2). A comparison of 10 biophysical models in TRENDY showed that the global GPP ranged from 107.8 to 154.9 Pg C yr−1 (Fig. 11a3). The revised EC-LUE model quantified the mean global GPP from 1982 to 2017 as 106.2±2.9 Pg C yr−1. Other studies also support the conclusion that there are large uncertainties in the GPP estimates. By comparing diverse GPP models and products, Anav et al. (2015) reported that the global GPP ranged from 112 to 169 Pg C yr−1. Seven satellite-based LUE models estimated the global GPP ranged from 95.1 to 139.7 Pg C yr−1 over the period of 2000–2010 (Cai et al., 2014).
The interannual variability and trend in GPP also vary substantially with different models. This study showed that the interannual variability (standard deviation) ranged from 0.32 to 5.89 Pg C yr−1, with the trends varying from −0.05 to 0.84 Pg C yr−1 (Fig. 11). The biophysical models showed large interannual variability, with the standard deviation ranging from 1.38 to 5.89 Pg C yr−1. The LUE models estimated the interannual variability varied from 1.30 to 3.13 Pg C yr−1. In contrast, the machine learning models exhibited less interannual variability with a standard deviation under 1.0 Pg C yr−1. The interannual variability of the revised EC-LUE model was 2.9 Pg C yr−1 (Fig. 11b1–b3). In general, the GPP interannual variability before the year 2000 was greater than that after the year 2001 for most of the biophysical models and LUE models (Fig. 11b1–b3). Most GPP models showed an increasing trend or insignificant trend during all valid years and before 2000. Similar to the standard deviation, the trends of machine learning models were less than other models. Compared with the other models, CLASS-CTEM and the revised EC-LUE model showed a significant decreasing trend after 2001 (Fig. 11c1–c3), probably because of the joint effect of increased VPD and decreased PAR (Fig. 8c).

Figure 10Comparisons of annual global summed GPP estimates from various models. The datasets or model algorithms were obtained from EC-LUE (Cai et al., 2014), MODIS (Smith et al., 2016), MOD17 C6 (Running et al., 2004), PR (Keenan et al., 2016), VPM (Zhang et al., 2017), FLUXCOM (Jung et al., 2017), SVR (Kondo et al., 2015), BESS (Jiang and Ryu, 2016), BEPS (Ju et al., 2006; Liu et al., 2018), and models in TRENDY (CABLE, CLASS-CTEM, CLM, ISAM, JSBACH, JULES, LPJ-GUESS, LPX-Bern, ORCHIDEE, and VISIT).
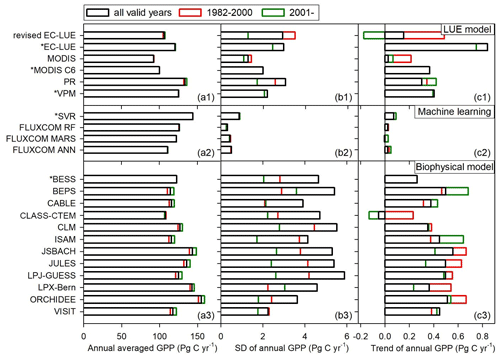
Figure 11Comparison of (a1)–(a3) averaged annual GPP, (b1)–(b3) interannual variability in annual GPP represented by standard deviation (SD), and (c1)–(c3) annual GPP trend among different GPP datasets or models. The references of these models are the same as in Fig. 9. The asterisk indicates that the valid period of the dataset begins from 2000 or 2001.
4.3 Model uncertainty
The uncertainties of our GPP dataset were low in high- and middle-latitude areas but high in tropical areas (Fig. 7). This is consistent with the validations at site level showing the revised EC-LUE model showed the lowest accuracy over the tropical evergreen broadleaf forest sites (Fig. 2). Similarly, other satellite-based models exhibited a large uncertainty in the GPP simulations over tropical forest areas (Ryu et al., 2011; Yuan et al., 2014). For example, the MODIS GPP product (MOD17) underestimated GPP at high-productivity sites over the tropical evergreen forests (de Almeida et al., 2018). Regarding the quality of satellite data, a high cloud cover exists over tropical regions, introducing large uncertainties to fraction of absorbed photosynthetically active radiation (FAPAR), LAI and other vegetation indices (e.g., normalized difference vegetation index, NDVI, and enhanced vegetation index, EVI). As suggested by de Almeida et al. (2018), the lack of reliable MOD15 FAPAR data from January to April as a result of the cloudiness contamination could have substantially affected the seasonality of GPP estimates. Besides, the quality of satellite data can even affect the evaluation of the interannual variations in GPP. Using MODIS EVI data, Saleska et al. (2007) reported a large-scale green-up in the Amazon evergreen forests during the drought of 2005. However, an opposite conclusion was drawn when the cloud-contaminated data were excluded from the analysis (Samanta et al., 2010). In our study, a significant decrease in GPP was found in the Amazon evergreen forests, which may result from the sharp increase in VPD after the late 1990s (Yuan et al., 2019). Studies using optical satellite data can be influenced by the cloudiness contamination. Recently studies using cloud-free satellite-based microwave data also reported a carbon loss in tropic forest (Liu et al., 2015; Fan et al., 2019).
The latest study highlighted that the aggregate canopy phenology rather than the climate changes is the main cause of the seasonal changes in photosynthesis in evergreen broadleaf forests (Wu et al., 2016). In particular, the new leaf growing synchronously with dry season litterfall may shift the old canopy to be younger, which can explain the significant seasonal increase (∼ 27 %) in the ecosystem photosynthesis. Therefore, the vertical changes in leaf age and photosynthesis ability with canopy depth are important to simulate the seasonal variations in carbon flux in tropical forests (Wu et al., 2017). These leaf-trait-related parameters can be simulated from the narrow-band spectra of leaves (Serbin et al., 2012; Dechant et al., 2017). Nevertheless, because of the limitation in obtaining the large-scale hyperspectral remote sensing data, regional or global estimation of these parameters is currently unavailable.
The revised EC-LUE model does not integrate the regulation of soil nitrogen content on vegetation production. Atmospheric nitrogen deposition has exhibited a large increasing trend in the past few decades because of the excessive fossil fuel combustion in the industrial and transportation sectors and the abuse of nitrogenous fertilizer in agricultural practices (Galloway et al., 2004). And the global land atmospheric nitrogen deposition is expected to further increase dramatically from 25 to 40 Tg N yr−1 in the 2000s to 60–100 Tg N yr−1 in 2100 (Lamarque et al., 2005). A meta-analysis of worldwide nitrogen addition experiments found that nitrogen addition could have a significantly positive effect on vegetation productivity (Liu and Greaver, 2009). As most terrestrial ecosystems are nitrogen limited, quantifying the spatiotemporal distributions of vegetation nitrogen content at large scales is essential to improve the accuracy of carbon flux estimation. Several studies quantified the leaf nitrogen content by detecting the nitrogen absorption spectra from the narrow band of hyperspectral data (Cho, 2007). However, leaf water, starch, lignin, and cellulose overlap with the absorption characters of nitrogen in the shortwave infrared bands, making it difficult to retrieve the nitrogen content (Kokaly and Clark, 1999). Additionally, canopy structures, background, and illumination/viewing geometry can further decrease the capacity to detect leaf nitrogen (Yoder and Pettigrew-Crosby, 1995; Knyazikhin et al., 2013). Advances in inversion and statistical models of leaf or canopy nitrogen have emerged (Asner et al., 2011; Dechant et al., 2017; Wang et al., 2018), but these methods require further evaluation over large regions, and the global map of leaf or canopy nitrogen is not available yet.
Additionally, the uncertainty of the revised EC-LUE model may arise by scale mismatches between eddy covariance flux footprint and input datasets. The eddy covariance flux footprint is generally less than 3 km2 and varies depending on the wind speed, wind direction, and atmospheric stability (Tan et al., 2006). In our studies, the revised EC-LUE model was run at 0.05∘ (∼ 5 km2) spatial resolution. The uncertainty of simulated GPP introduced by the scale effect is inevitable but smaller than that introduced by the model structures, parameters, or input datasets (Sjostrom et al., 2013; Zheng et al., 2018).
The global GPP dataset for 1982–2017 is available at https://doi.org/10.6084/m9.figshare.8942336.v3 (Zheng et al., 2019). The dataset is provided in HDF format at an 8 d interval. The valid value ranges from 0 to 3000, and the background filled value is 65 535. The scale factor of the data is 0.01. Each HDF file represents an 8 d GPP at a daily value (unit: g C m−2 d−1). To obtain the summation of each 8 d (or 5 d or 6 d) period, please multiply the GPP value by the corresponding days (8 for the first 45 values and 5 or 6 for the last value in a year).
In this study, we produced a long-term global GPP dataset by integrating several major long-term environmental variables into a light use efficiency model, including atmospheric CO2 concentration, radiation components, and atmospheric water vapor pressure. These environmental variables showed substantial long-term changes and contributed significantly to vegetation production at an interannual scale. The revised EC-LUE model performed well in simulating the spatial, seasonal, and interannual variations in GPP across the globe. In particular, it has a unique superiority in reproducing the interannual variations in GPP (R2=0.44) compared with the original EC-LUE model (R2=0.36) and other LUE models (R2 ranged from 0.06 to 0.30 with an average value of 0.16). The GPP dataset derived from the revised EC-LUE model provides an alternative and reliable estimate of global GPP at the long-term scale by integrating the important environmental variables.
The supplement related to this article is available online at: https://doi.org/10.5194/essd-12-2725-2020-supplement.
WY and YZ designed the research, performed the analysis, and wrote the paper; RS, YW, and XL performed the analysis; SLiu, SLiang, JC, WJ, and LZ edited and revised the manuscript.
The authors declare that they have no conflict of interest.
The covariance data used in the study were acquired and shared by the FLUXNET community, including the following networks: AmeriFlux, AfriFlux, AsiaFlux, CarboAfrica, CarboEuropeIP, CarboItaly, CarboMont, ChinaFlux, Fluxnet-Canada, GreenGrass, ICOS, KoFlux, LBA, NECC, OzFlux-TERN, TCOS-Siberia, and USCCC. The ERA-Interim reanalysis data are provided by ECMWF and processed by LSCE. The FLUXNET eddy covariance data processing and harmonization was carried out by the European Fluxes Database Cluster, AmeriFlux Management Project, and Fluxdata project of FLUXNET, with the support of CDIAC and ICOS Ecosystem Thematic Center, and the OzFlux, ChinaFlux, and AsiaFlux offices.
This research has been supported by the National Science Fund for Distinguished Young Scholars (41925001) and National Key Basic Research Program of China (grant no. 2016YFA0602701).
This paper was edited by Yuyu Zhou and reviewed by three anonymous referees.
Ainsworth, E. A. and Long, S. P.: What have we learned from 15 years of free-air CO2 enrichment (FACE)? A meta-analytic review of the responses of photosynthesis, canopy, New Phytol., 165, 351–371, https://doi.org/10.1111/j.1469-8137.2004.01224.x, 2005.
Alton, P. B., North, P. R., and Los, S. O.: The impact of diffuse sunlight on canopy light-use efficiency, gross photosynthetic product and net ecosystem exchange in three forest biomes, Global Change Biol., 13, 776–787, https://doi.org/10.1111/j.1365-2486.2007.01316.x, 2007.
Anav, A., Friedlingstein, P., Beer, C., Ciais, P., Harper, A., Jones, C., Murray-Tortarolo, G., Papale, D., Parazoo, N.C., Peylin, P., Piao, S., Sitch, S., Viovy, N., Wiltshire, A., and Zhao, M.: Spatiotemporal patterns of terrestrial gross primary production: A review, Rev. Geophys., 53, 785–818, https://doi.org/10.1002/2015rg000483, 2015.
Asner, G. P., Martin, R. E., Knapp, D. E., Tupayachi, R., Anderson, C., Carranza, L., Martinez, P., Houcheime, M., Sinca, F., and Weiss, P.: Spectroscopy of canopy chemicals in humid tropical forests, Remote Sens. Environ., 115, 3587–3598, https://doi.org/10.1016/j.rse.2011.08.020, 2011.
Beck, H. E., Zimmermann, N. E., McVicar, T. R., Vergopolan, N., Berg, A., and Wood, E. F.: Present and future Koppen-Geiger climate classification maps at 1-km resolution, Sci. Data, 5, 180214, https://doi.org/10.1038/sdata.2018.214, 2018.
Cai, W., Yuan, W., Liang, S., Zhang, X., Dong, W., Xia, J., Fu, Y., Chen, Y., Liu, D., and Zhang, Q.: Improved estimations of gross primary production using satellite-derived photosynthetically active radiation, J. Geophys. Res.-Biogeo., 119, 110–123, https://doi.org/10.1002/2013jg002456, 2014.
Cai, W., Yuan, W., Liang, S., Liu, S., Dong, W., Chen, Y., Liu, D., and Zhang, H.: Large Differences in Terrestrial Vegetation Production Derived from Satellite-Based Light Use Efficiency Models, Remote Sens., 6, 8945–8965, https://doi.org/10.3390/rs6098945, 2014.
Canadell, J. G., Le Quere, C., Raupach, M. R., Field, C. B., Buitenhuis, E. T., Ciais, P., Conway, T. J., Gillett, N. P., Houghton, R. A., and Marland, G.: Contributions to accelerating atmospheric CO2 growth from economic activity, carbon intensity, and efficiency of natural sinks, P. Natl. Acad. Sci. USA, 104, 18866–18870, https://doi.org/10.1073/pnas.0702737104, 2007.
Chen, J. M., Liu, J., Cihlar, J., and Goulden, M. L.: Daily canopy photosynthesis model through temporal and spatial scaling for remote sensing applications, Ecol. Model., 124, 99–119, https://doi.org/10.1016/s0304-3800(99)00156-8, 1999.
Cho, M. A., Skidmore, A., Corsi, F., van Wieren, S. E., and Sobhan, I.: Estimation of green grass/herb biomass from airborne hyperspectral imagery using spectral indices and partial least squares regression, Int. J. Appl. Earth Observ. Geoinfo., 9, 414–424, https://doi.org/10.1016/j.jag.2007.02.001, 2007.
Clark, D. B., Mercado, L. M., Sitch, S., Jones, C. D., Gedney, N., Best, M. J., Pryor, M., Rooney, G. G., Essery, R. L. H., Blyth, E., Boucher, O., Harding, R. J., Huntingford, C., and Cox, P. M.: The Joint UK Land Environment Simulator (JULES), model description – Part 2: Carbon fluxes and vegetation dynamics, Geosci. Model Dev., 4, 701–722, https://doi.org/10.5194/gmd-4-701-2011, 2011.
Collatz, G. J., Ball, J. T., Grivet, C., and Berry, J. A.: Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: a model that includes a laminar boundary layer, Agr. Forest. Meteorol., 54, 107–136, 1991.
de Almeida, C. T., Delgado, R. C., Galvao, L. S., de Oliveira Cruz e Aragao, L. E., and Concepcion Ramos, M.: Improvements of the MODIS Gross Primary Productivity model based on a comprehensive uncertainty assessment over the Brazilian Amazonia, ISPRS J. Photogramm. Remote Sens., 145, 268–283, https://doi.org/10.1016/j.isprsjprs.2018.07.016, 2018.
de Cárcer, P. S., Vitasse, Y., Peñuelas, J., Jassey, V. E. J., Buttler, A., and Signarbieux, C.: Vapor-pressure deficit and extreme climatic variables limit tree growth, Global Change Biol., 24, 1108–1122, https://doi.org/10.1111/gcb.13973, 2018.
Dechant, B., Cuntz, M., Vohland, M., Schulz, E., and Doktor, D.: Estimation of photosynthesis traits from leaf reflectance spectra: Correlation to nitrogen content as the dominant mechanism, Remote Sens. Environ., 196, 279–292, https://doi.org/10.1016/j.rse.2017.05.019, 2017.
Ding, J., Yang, T., Zhao, Y., Liu, D., Wang, X., Yao, Y., Peng, S., Wang, T., and Piao, S.: Increasingly Important Role of Atmospheric Aridity on Tibetan Alpine Grasslands, Geophys. Res. Lett., 45, 2852–2859, https://doi.org/10.1002/2017gl076803, 2018.
Fan, L., Wigneron, J.-P., Ciais, P., Chave, J., Brandt, M., Fensholt, R., Saatchi, S. S., Bastos, A., Al-Yaari, A., Hufkens, K., Qin, Y., Xiao, X., Chen, C., Myneni, R. B., Fernandez-Moran, R., Mialon, A., Rodriguez-Fernandez, N. J., Kerr, Y., Tian, F., and Penuelas, J.: Satellite-observed pantropical carbon dynamics, Nat. Plants, 5, 944–951, 2019.
Farquhar, G.D., von Caemmerer, S., and Berry, J. A.: A biochemical model of photosynthetic CO2 assimilation in leaves of C 3 species, Planta, 149, 78–90, https://doi.org/10.1007/bf00386231, 1980.
Fletcher, A. L., Sinclair, T. R., and Allen, L. H.: Transpiration responses to vapor pressure deficit in well watered “slow-wilting” and commercial soybean, Environ. Exp. Bot., 61, 145–151, https://doi.org/10.1016/j.envexpbot.2007.05.004, 2007.
Galloway, J. N., Dentener, F. J., Capone, D. G., Boyer, E. W., Howarth, R. W., Seitzinger, S. P., Asner, G. P., Cleveland, C. C., Green, P. A., Holland, E. A., Karl, D. M., Michaels, A. F., Porter, J. H., Townsend, A. R., and Vorosmarty, C. J.: Nitrogen cycles: past, present, and future, Biogeochemistry, 70, 153–226, https://doi.org/10.1007/s10533-004-0370-0, 2004.
Gilgen, H., Wild, M., and Ohmura, A.: Means and trends of shortwave irradiance at the surface estimated from Global Energy Balance Archive data, J. Clim., 11, 2042–2061, https://doi.org/10.1175/1520-0442-11.8.2042, 1998.
Gu, L. H., Baldocchi, D., Verma, S. B., Black, T. A., Vesala, T., Falge, E. M., and Dowty, P. R.: Advantages of diffuse radiation for terrestrial ecosystem productivity, J. Geophys. Res.-Atmos., 107, ACL 2-1–ACL 2-23, https://doi.org/10.1029/2001jd001242, 2002.
Gu, L. H., Baldocchi, D. D., Wofsy, S. C., Munger, J. W., Michalsky, J. J., Urbanski, S. P., and Boden, T. A.: Response of a deciduous forest to the Mount Pinatubo eruption: Enhanced photosynthesis, Science, 299, 2035–2038, https://doi.org/10.1126/science.1078366, 2003.
Jiang, C. and Ryu, Y.: Multi-scale evaluation of global gross primary productivity and evapotranspiration products derived from Breathing Earth System Simulator (BESS), Remote Sens. Environ., 186, 528–547, 2016.
Ju, W., Chen, J. M., Black, T. A., Barr, A. G., Liu, J., and Chen, B.: Modelling multi-year coupled carbon and water fluxes in a boreal aspen forest, Agr. Forest Meteorol., 140, 136–151, https://doi.org/10.1016/j.agrformet.2006.08.008, 2006.
Jain, A. K., Meiyappan, P., Song, Y., and House, J. I.: CO2 Emissions from Land-Use Change Affected More by Nitrogen Cycle, than by the Choice of Land Cover Data, Glob. Change Biol., 9, 2893–2906, 2013.
Jung, M., Reichstein, M., Schwalm, C. R., Huntingford, C., Sitch, S., Ahlstrom, A., Arneth, A., Camps-Valls, G., Ciais, P., Friedlingstein, P., Gans, F., Ichii, K., Ain, A. K. J., Kato, E., Papale, D., Poulter, B., Raduly, B., Rodenbeck, C., Tramontana, G., Viovy, N., Wang, Y.-P., Weber, U., Zaehle, S., and Zeng, N.: Compensatory water effects link yearly global land CO2 sink changes to temperature, Nature, 541, 516–520, https://doi.org/10.1038/nature20780, 2017.
Kanji, G. K.: 100 Statistical Tests, SAGE Publications, London, 1999.
Kanniah, K. D., Beringer, J., North, P., and Hutley, L.: Control of atmospheric particles on diffuse radiation and terrestrial plant productivity: A review, Progr. Phys. Geogr., 36, 209–237, https://doi.org/10.1177/0309133311434244, 2012.
Kato, E., Kinoshita, T., Ito, A., Kawamiya, M., and Yamagata, Y.: Evaluation of spatially explicit emission scenario of land-use change and biomass burning using a process-based biogeochemical model, J. Land Use Sci., 8, 104–122, 2013.
Keenan, T. F., Baker, I., Barr, A., Ciais, P., Davis, K., Dietze, M., Dragon, D., Gough, C. M., Grant, R., Hollinger, D., Hufkens, K., Poulter, B., McCaughey, H., Raczka, B., Ryu, Y., Schaefer, K., Tian, H., Verbeeck, H., Zhao, M., and Richardson, A. D.: Terrestrial biosphere model performance for inter-annual variability of land-atmosphere CO2 exchange, Global Change Biol., 18, 1971–1987, https://doi.org/10.1111/j.1365-2486.2012.02678.x, 2012.
Keenan, T. F., Prentice, I. C., Canadell, J. G., Williams, C. A., Wang, H., Raupach, M., and Collatz, G. J.: Recent pause in the growth rate of atmospheric CO2 due to enhanced terrestrial carbon uptake, Nat. Commun., 7, 13428, https://doi.org/10.1038/ncomms13428, 2016.
Khair, U., Fahmi, H., Al Hakim, S., and Rahim, R.: Forecasting Error Calculation with Mean Absolute Deviation and Mean Absolute Percentage Error, J. Phys. Conf. Ser., 930, 012002, https://doi.org/10.1088/1742-6596/930/1/012002, 2017.
King, D. A., Turner, D. P., and Ritts, W. D.: Parameterization of a diagnostic carbon cycle model for continental scale application, Remote Sens. Environ., 1157, 1653–1664, 2011.
Knyazikhin, Y., Schull, M. A., Stenberg, P., Mottus, M., Rautiainen, M., Yang, Y., Marshak, A., Latorre Carmona, P., Kaufmann, R. K., Lewis, P., Disney, M. I., Vanderbilt, V., Davis, A. B., Baret, F., Jacquemoud, S., Lyapustin, A., and Myneni, R. B.: Hyperspectral remote sensing of foliar nitrogen content, Proc. Natl. Acad. Sci. USA, 110, E185–E192, https://doi.org/10.1073/pnas.1210196109, 2013.
Kokaly, R. F. and Clark, R. N.: Spectroscopic determination of leaf biochemistry using band-depth analysis of absorption features and stepwise multiple linear regression, Remote Sens. Environ., 67, 267–287, https://doi.org/10.1016/s0034-4257(98)00084-4, 1999.
Kondo, M., Ichii, K., Takagi, H., and Sasakawa, M.: Comparison of the data-driven top-down and bottom-up global terrestrial CO2 exchanges: GOSAT CO2 inversion and empirical eddy flux upscaling, J. Geophys. Res.-Biogeo., 120, 1226–1245, 2015.
Konings, A. G., Williams, A. P., and Gentine, P.: Sensitivity of grassland productivity to aridity controlled by stomatal and xylem regulation, Nat. Geosci., 10, 284–288, https://doi.org/10.1038/ngeo2903, 2017.
Korson, L., Drost-Hansen, W., and Millero, F. J.: Viscosity of water at various temperatures, J. Phys. Chem., 73, 34–39, https://doi.org/10.1021/j100721a006, 1969.
Krinner, G., Viovy, N., de Noblet, N., Ogée, J., Friedlingstein, P., Ciais, P., Sitch, S., Polcher, J., and Prentice, I. C.: A dynamic global vegetation model for studies of the coupled atmospherebiosphere system, Global Biogeochem. Cy., 19, 1–33, 2005.
Krupkova, L., Markova, I., Havrankova, K., Pokorny, R., Urban, O., Sigut, L., Pavelka, M., Cienciala, E., and Marek, M. V.: Comparison of different approaches of radiation use efficiency of biomass formation estimation in Mountain Norway spruce, Trees-Struct. Funct., 31, 325–337, https://doi.org/10.1007/s00468-016-1486-2, 2017.
Lamarque, J. F., Kiehl, J. T., Brasseur, G. P., Butler, T., Cameron-Smith, P., Collins, W. D., Collins, W. J., Granier, C., Hauglustaine, D., Hess, P. G., Holland, E. A., Horowitz, L., Lawrence, M. G., McKenna, D., Merilees, P., Prather, M. J., Rasch, P. J., Rotman, D., Shindell, D., and Thornton, P.: Assessing future nitrogen deposition and carbon cycle feedback using a multimodel approach: Analysis of nitrogen deposition, J. Geophys. Res.-Atmos., 11, D19303, https://doi.org/10.1029/2005jd005825, 2005.
Le Quéré, C., Andrew, R. M., Canadell, J. G., Sitch, S., Korsbakken, J. I., Peters, G. P., Manning, A. C., Boden, T. A., Tans, P. P., Houghton, R. A., Keeling, R. F., Alin, S., Andrews, O. D., Anthoni, P., Barbero, L., Bopp, L., Chevallier, F., Chini, L. P., Ciais, P., Currie, K., Delire, C., Doney, S. C., Friedlingstein, P., Gkritzalis, T., Harris, I., Hauck, J., Haverd, V., Hoppema, M., Klein Goldewijk, K., Jain, A. K., Kato, E., Körtzinger, A., Landschützer, P., Lefèvre, N., Lenton, A., Lienert, S., Lombardozzi, D., Melton, J. R., Metzl, N., Millero, F., Monteiro, P. M. S., Munro, D. R., Nabel, J. E. M. S., Nakaoka, S., O'Brien, K., Olsen, A., Omar, A. M., Ono, T., Pierrot, D., Poulter, B., Rödenbeck, C., Salisbury, J., Schuster, U., Schwinger, J., Séférian, R., Skjelvan, I., Stocker, B. D., Sutton, A. J., Takahashi, T., Tian, H., Tilbrook, B., van der Laan-Luijkx, I. T., van der Werf, G. R., Viovy, N., Walker, A. P., Wiltshire, A. J., and Zaehle, S.: Global Carbon Budget 2016, Earth Syst. Sci. Data, 8, 605–649, https://doi.org/10.5194/essd-8-605-2016, 2016.
Li, X. L., Liang, S. L., Yu, G. R., Yuan, W. P., Cheng, X., Xia, J. Z., Zhao, T. B., Feng, J. M., Ma, Z. G., Ma, M. G., Liu, S. M., Chen, J. Q., Shao, C. L., Li, S. G., Zhang, X. D., Zhang, Z. Q., Chen, S. P., Ohta, T., Varlagin, A., Miyata, A., Takagi, K., Saiqusa, N., and Kato, T.: Estimation of gross primary production over the terrestrial ecosystems in China, Ecol. Model., 261, 80–92, https://doi.org/10.1016/j.ecolmodel.2013.03.024, 2013.
Liu, L. and Greaver, T. L.: A review of nitrogen enrichment effects on three biogenic GHGs: the CO2 sink may be largely offset by stimulated N2O and CH4 emission, Ecol. Lett., 12, 1103–1117, https://doi.org/10.1111/j.1461-0248.2009.01351.x, 2009.
Liu, S., Bond-Lamberty, B., Boysen, L. R., Ford, J. D., Fox, A., Gallo, K., Hatfield, J., Henebry, G. M., Huntington, T. G., Liu, Z., Loveland, T. R., Norby, R. J., Sohl, T., Steiner, A. L., Yuan, W., Zhang, Z., and Zhao, S.: Grand Challenges in Understanding the Interplay of Climate and Land Changes, Earth Interactions, 21, 1–43, https://doi.org/10.1175/ei-d-16-0012.1, 2017.
Liu, Y., Xiao, J., Ju, W., Zhu, G., Wu, X., Fan, W., Li, D., and Zhou, Y.: Satellite-derived LAI products exhibit large discrepancies and can lead to substantial uncertainty in simulated carbon and water fluxes, Remote Sens. Environ., 206, 174–188, https://doi.org/10.1016/j.rse.2017.12.024, 2018.
Liu, Y. Y., van Dijk, A. I. J. M., de Jeu, R. A. M., Canadell, J. G., McCabe, M. F., Evans, J. P., and Wang, G.: Recent reversal in loss of global terrestrial biomass, Nat. Clim. Change, 5, 470–474, 2015.
Lobell, D. B., Roberts, M. J., Schlenker, W., Braun, N., Little, B. B., Rejesus, R. M., and Hammer, G. L.: Greater Sensitivity to Drought Accompanies Maize Yield Increase in the US Midwest, Science, 344, 516–519, https://doi.org/10.1126/science.1251423, 2014.
Monteith, J.: Solar radiation and productivity in tropical ecosystems, J. Appl. Ecol., 9, 747–766, 1972.
Mahadevan, P., Wofsy, S. C., Matross, D. M., Xiao, X. M., Dunn, A. L., Lin, J. C., Gerbig, C., Munger, J. W., Chow, V. Y., and Gottlieb, E. W.: A satellite-based biosphere parameterization for net ecosystem CO2 exchange: Vegetation Photosynthesis and Respiration Model VPRM, Global Biogeochem. Cy., 222, 1–17, 2008.
Melton, J. R. and Arora, V. K.: Competition between plant functional types in the Canadian Terrestrial Ecosystem Model (CTEM) v. 2.0, Geosci. Model Dev., 9, 323–361, https://doi.org/10.5194/gmd-9-323-2016, 2016.
Norby, R. J., DeLucia, E. H., Gielen, B., Calfapietra, C., Giardina, C. P., King, J. S., Ledford, J., McCarthy, H. R., Moore, D. J. P., Ceulemans, R., De Angelis, P., Finzi, A. C., Karnosky, D. F., Kubiske, M. E., Lukac, M., Pregitzer, K. S., Scarascia-Mugnozza, G. E., Schlesinger, W. H., and Oren, R.: Forest response to elevated CO2 is conserved across a broad range of productivity, P. Natl. Acad. Sci. USA, 102, 18052–18056, https://doi.org/10.1073/pnas.0509478102, 2005.
Norby, R. J., Wullschleger, S. D., Gunderson, C. A., Johnson, D. W., and Ceulemans, R.: Tree responses to rising CO2 in field experiments: implications for the future forest, Plant Cell Environ., 22, 683–714, https://doi.org/10.1046/j.1365-3040.1999.00391.x, 1999.
Novick, K. A., Ficklin, D. L., Stoy, P. C., Williams, C. A., Bohrer, G., Oishi, A. C., Papuga, S. A., Blanken, P. D., Noormets, A., Sulman, B. N., Scott, R. L., Wang, L., and Phillips, R. P.: The increasing importance of atmospheric demand for ecosystem water and carbon fluxes, Nat. Clim. Change, 6, 1023–1027, https://doi.org/10.1038/nclimate3114, 2016.
Oleson, K. W., Lawrence, D. M., Bonan, G. B., Drewniak, B., Huang, M., Koven, C. D., Levis, S., Li, F., Riley, W. J., Subin, Z. M., Swenson, S. C., Thornton, P. E., Bozbiyik, A., Fisher, R., Heald, C. L., Kluzek, E., Lamarque, J., Lawrence, P. J., Leung, L. R., Lipscomb, W., Muszala, S., Ricciuto, D. M., Sacks, W., Tang, J., and Yang, Z.: Technical description of version 4.5 of the community land model (CLM), NCAR Tech. Note, NCAR/TN-503+ STR, 420, https://doi.org/0.5065/D6RR1W7M, 2013.
Piao, S., Sitch, S., Ciais, P., Friedlingstein, P., Peylin, P., Wang, X., Ahlstrom, A., Anav, A., Canadell, J. G., Cong, N., Huntingford, C., Jung, M., Levis, S., Levy, P. E., Li, J., Lin, X., Lomas, M.R., Lu, M., Luo, Y., Ma, Y., Myneni, R. B., Poulter, B., Sun, Z., Wang, T., Viovy, N., Zaehle, S., and Zeng, N.: Evaluation of terrestrial carbon cycle models for their response to climate variability and to CO2 trends, Global Change Biol., 19, 2117–2132, https://doi.org/10.1111/gcb.12187, 2013.
Pierce, D. W., Westerling, A. L., and Oyler, J.: Future humidity trends over the western United States in the CMIP5 global climate models and variable infiltration capacity hydrological modeling system, Hydrol. Earth Syst. Sci., 17, 1833–1850, https://doi.org/10.5194/hess-17-1833-2013, 2013.
Potter, C. S., Randerson, J. T., Field, C. B., Matson, P. A., Vitousek, P. M., Mooney, H. A., and Klooster, S. A.: Terrestrial ecosystem production: A process model-based on global satellite and surface data, Global Biogeochem. Cy., 7, 811–841, https://doi.org/10.1029/93gb02725, 1993.
Prentice, I. C., Dong, N., Gleason, S. M., Maire, V., and Wright, I. J.: Balancing the costs of carbon gain and water transport: testing a new theoretical framework for plant functional ecology, Ecol. Lett., 17, 82–91, https://doi.org/10.1111/ele.12211, 2014.
Rawson, H. M., Begg, J. E., and Woodward, R. G.: The effect of atmospheric humidity on photosynthesis, transpiration and water use efficiency of leaves of several plant species, Planta, 134, 5–10, https://doi.org/10.1007/bf00390086, 1977.
Reichstein, M., Falge, E., Baldocchi, D., Papale, D., Aubinet, M., Berbigier, P., Bernhofer, C., Buchmann, N., Gilmanov, T., Granier, A., Grunwald, T., Havrankova, K., Ilvesniemi, H., Janous, D., Knohl, A., Laurila, T., Lohila, A., Loustau, D., Matteucci, G., Meyers, T., Miglietta, F., Ourcival, J.-M., Pumpanen, J., Rambal, S., Rotenberg, E., Sanz, M., Tenhunen, J., Seufert, G., Vaccari, F., Vesala, T., Yakir, D., and Valentini, R.: On the separation of net ecosystem exchange into assimilation and ecosystem respiration: review and improved algorithm, Glob. Change Biol., 11, 1424–1439, https://doi.org/10.1111/j.1365-2486.2005.001002.x, 2005.
Reick, C. H., Raddatz, T., Brovkin, V., and Gayler, V.: The representation of natural and anthropogenic land cover change in MPIESM, J. Adv. Model. Earth Syst., 5, 459–482, 2013.
Rienecker, M. M., Suarez, M. J., Gelaro, R., Todling, R., Bacmeister, J., Liu, E., Bosilovich, M. G., Schubert, S. D., Takacs, L., Kim, G.-K., Bloom, S., Chen, J., Collins, D., Conaty, A., Da Silva, A., Gu, W., Joiner, J., Koster, R. D., Lucchesi, R., Molod, A., Owens, T., Pawson, S., Pegion, P., Redder, C. R., Reichle, R., Robertson, F. R., Ruddick, A. G., Sienkiewicz, M., and Woollen, J.: MERRA: NASA's modern-era retrospective analysis for research and applications, J. Clim., 24, 3624–3648, https://doi.org/10.1175/jcli-d-11-00015.1, 2011.
Running, S. W., Nemani, R. R., Heinsch, F. A., Zhao, M. S., Reeves, M., and Hashimoto, H.: A continuous satellite-derived measure of global terrestrial primary production, Bioscience, 54, 547–560, https://doi.org/10.1641/0006-3568(2004)054[0547:acsmog]2.0.co;2, 2004.
Ryu, Y., Baldocchi, D. D., Kobayashi, H., van Ingen, C., Li, J., Black, T. A., Beringer, J., van Gorsel, E., Knohl, A., Law, B. E., and Roupsard, O.: Integration of MODIS land and atmosphere products with a coupled-process model to estimate gross primary productivity and evapotranspiration from 1 km to global scales, Global Biogeochem. Cy., 25, GB4017, https://doi.org/10.1029/2011gb004053, 2011.
Ryu, Y., Berry, J. A., and Baldocchi, D. D.: What is global photosynthesis? History, uncertainties and opportunities, Remote Sens. Environ., 223, 95–114, https://doi.org/10.1016/j.rse.2019.01.016, 2019.
Saleska, S. R., Didan, K., Huete, A. R., and da Rocha, H. R.: Amazon forests green-up during 2005 drought, Science, 318, 612–612, https://doi.org/10.1126/science.1146663, 2007.
Samanta, A., Ganguly, S., Hashimoto, H., Devadiga, S., Vermote, E., Knyazikhin, Y., Nemani, R. R., and Myneni, R. B.: Amazon forests did not green-up during the 2005 drought, Geophys. Res. Lett., 37, L05401, https://doi.org/10.1029/2009gl042154, 2010.
Serbin, S. P., Dillaway, D. N., Kruger, E. L., and Townsend, P. A.: Leaf optical properties reflect variation in photosynthetic metabolism and its sensitivity to temperature, J. Exp. Bot., 63, 489–502, https://doi.org/10.1093/jxb/err294, 2012.
Simmons, A. J., Willett, K. M., Jones, P. D., Thorne, P. W., and Dee, D. P.: Low-frequency variations in surface atmospheric humidity, temperature, and precipitation: Inferences from reanalyses and monthly gridded observational data sets, J. Geophys. Res.-Atmos., 115, D01110, https://doi.org/10.1029/2009jd012442, 2010.
Sjostrom, M., Zhao, M., Archibald, S., Arneth, A., Cappelaere, B., Falk, U., de Grandcourt, A., Hanan, N., Kergoat, L., Kutsch, W., Merbold, L., Mougin, E., Nickless, A., Nouvellon, Y., Scholes, R. J., Veenendaal, E. M., and Ardo, J.: Evaluation of MODIS gross primary productivity for Africa using eddy covariance data, Remote Sens. Environ., 131, 275–286, https://doi.org/10.1016/j.rse.2012.12.023, 2013.
Smith, B., Wårlind, D., Arneth, A., Hickler, T., Leadley, P., Siltberg, J., and Zaehle, S.: Implications of incorporating N cycling and N limitations on primary production in an individual-based dynamic vegetation model, Biogeosciences, 11, 2027–2054, https://doi.org/10.5194/bg-11-2027-2014, 2014.
Smith, W. K., Reed, S. C., Cleveland, C. C., Ballantyne, A. P., Anderegg, W. R. L., Wieder, W. R., Liu, Y. Y., and Running, S. W.: Large divergence of satellite and Earth system model estimates of global terrestrial CO2 fertilization, Nat. Clim. Change, 6, 306–310, https://doi.org/10.1038/nclimate2879, 2016.
Stocker, B. D., Feissli, F., Strassmann, K. M., Spahni, R., and Joos, F.: Past and future carbon fluxes from land use change, shifting cultivation and wood harvest, Tellus B, 66, 23188, https://doi.org/10.3402/tellusb.v66.23188, 2014.
Stocker, B. D., Zscheischler, J., Keenan, T. F., Prentice, I. C., Seneviratne, S. I., and Peñuelas, J.: Drought impacts on terrestrial primary production underestimated by satellite monitoring, Nat. Geosci., 12, 264–270, https://doi.org/10.1038/s41561-019-0318-6, 2019.
Sulman, B. N., Roman, D. T., Yi, K., Wang, L., Phillips, R. P., and Novick, K. A.: High atmospheric demand for water can limit forest carbon uptake and transpiration as severely as dry soil, Geophys. Res. Lett., 43, 9686–9695, https://doi.org/10.1002/2016gl069416, 2016.
Tan, B., Woodcock, C. E., Hu, J., Zhang, P., Ozdogan, M., Huang, D., Yang, W., Knyazikhin, Y., and Myneni, R. B.: The impact of gridding artifacts on the local spatial properties of MODIS data: Implications for validation, compositing, and band-to-band registration across resolutions, Remote Sens. Environ., 105, 98–114, https://doi.org/10.1016/j.rse.2006.06.008, 2006.
Tang, S., Chen, J. M., Zhu, Q., Li, X., Chen, M., Sun, R., Zhou, Y., Deng, F., and Xie, D.: LAI inversion algorithm based on directional reflectance kernels, J. Environ. Manage., 85, 638–648, https://doi.org/10.1016/j.jenvman.2006.08.018, 2007.
Turner, D. P., Ritts, W. D., Styles, J. M., Yang, Z., Cohen, W. B., Law, B. E., and Thornton, P. E.: A diagnostic carbon flux model to monitor the effects of disturbance and interannual variation in climate on regional NEP, Tellus B, 585, 476–490, 2006.
Urban, O., Janous, D., Acosta, M., Czerny, R., Markova, I., Navratil, M., Pavelka, M., Pokorny, R., Sprtova, M., Zhang, R., Spunda, V., Grace, J., and Marek, M. V.: Ecophysiological controls over the net ecosystem exchange of mountain spruce stand. Comparison of the response in direct vs. diffuse solar radiation, Global Change Biol., 13, 157–168, https://doi.org/10.1111/j.1365-2486.2006.01265.x, 2007.
Van Wijngaarden, W. A. and Vincent, L. A.: Trends in relative humidity in Canada from 1953–2003, B. Am. Meteorol. Soc., 4633–4636, 2004.
Veroustraete, F., Sabbe, H., and Eerens, H.: Estimation of carbon mass fluxes over Europe using the C-Fix model and Euroflux data, Remote Sens. Environ., 833, 376–399, 2002.
Vuichard, N. and Papale, D.: Filling the gaps in meteorological continuous data measured at FLUXNET sites with ERA-Interim reanalysis, Earth Syst. Sci. Data, 7, 157–171, https://doi.org/10.5194/essd-7-157-2015, 2015.
Wang, Z., Skidmore, A. K., Darvishzadeh, R., and Wang, T.: Mapping forest canopy nitrogen content by inversion of coupled leaf-canopy radiative transfer models from airborne hyperspectral imagery, Agr. Forest. Meteorol., 253, 247–260, https://doi.org/10.1016/j.agrformet.2018.02.010, 2018.
Wild, M., Gilgen, H., Roesch, A., Ohmura, A., Long, C.N., Dutton, E.G., Forgan, B., Kallis, A., Russak, V., and Tsvetkov, A.: From dimming to brightening: Decadal changes in solar radiation at Earth's surface, Science, 308, 847–850, https://doi.org/10.1126/science.1103215, 2005.
Willett, K. M., Dunn, R. J. H., Thorne, P. W., Bell, S., de Podesta, M., Parker, D. E., Jones, P. D., and Williams Jr., C. N.: HadISDH land surface multi-variable humidity and temperature record for climate monitoring, Clim. Past, 10, 1983–2006, https://doi.org/10.5194/cp-10-1983-2014, 2014.
Williams, A. P., Allen, C. D., Macalady, A. K., Griffin, D., Woodhouse, C. A., Meko, D. M., Swetnam, T. W., Rauscher, S. A., Seager, R., Grissino-Mayer, H. D., Dean, J. S., Cook, E. R., Gangodagamage, C., Cai, M., and McDowell, N. G.: Temperature as a potent driver of regional forest drought stress and tree mortality, Nat. Clim. Change, 3, 292–297, https://doi.org/10.1038/nclimate1693, 2013.
Wu, J., Albert, L. P., Lopes, A. P., Restrepo-Coupe, N., Hayek, M., Wiedemann, K. T., Guan, K., Stark, S. C., Christoffersen, B., Prohaska, N., Tavares, J. V., Marostica, S., Kobayashi, H., Ferreira, M. L., Campos, K. S., da Silva, R., Brando, P. M., Dye, D. G., Huxman, T. E., Huete, A. R., Nelson, B. W., and Saleska, S. R.: Leaf development and demography explain photosynthetic seasonality in Amazon evergreen forests, Science, 351, 972–976, https://doi.org/10.1126/science.aad5068, 2016.
Wu, J., Guan, K., Hayek, M., Restrepo-Coupe, N., Wiedemann, K. T., Xu, X., Wehr, R., Christoffersen, B. O., Miao, G., da Silva, R., de Araujo, A. C., Oliviera, R. C., Camargo, P. B., Monson, R. K., Huete, A. R., and Saleska, S. R.: Partitioning controls on Amazon forest photosynthesis between environmental and biotic factors at hourly to interannual timescales, Global Change Biol., 23, 1240–1257, https://doi.org/10.1111/gcb.13509, 2017.
Xiao, X. M., Zhang, Q. Y., Hollinger, D., Aber, J., and Moore, B.: Modeling gross primary production of an evergreen needleleaf forest using MODIS and climate data, Ecol. Appl., 15, 954–969, https://doi.org/10.1890/04-0470, 2005.
Xiao, Z., Liang, S., Wang, J., Xiang, Y., Zhao, X., and Song, J.: Long-Time-Series Global Land Surface Satellite Leaf Area Index Product Derived From MODIS and AVHRR Surface Reflectance, IEEE Trans. Geosci. Remote, 54, 5301–5318, https://doi.org/10.1109/tgrs.2016.2560522, 2016.
Xu, B., Li, J., Park, T., Liu, Q., Zeng, Y., Yin, G., Zhao, J., Fan, W., Yang, L., Knyazikhin, Y., Myneni, R. B.: An integrated method for validating long-term leaf area index products using global networks of site-based measurements, Remote Sens. Environ., 209, 134–151, https://doi.org/10.1016/j.rse.2018.02.049, 2018.
Yoder, B. J. and Pettigrew-Crosby, R. E.: Predicting nitrogen and chlorophyll content and concentrations from reflectance spectra (400–2500 nm) at leaf and canopy scales, Remote Sens. Environ., 53, 199–211, https://doi.org/10.1016/0034-4257(95)00135-n, 1995.
Yuan, W., Cai, W., Xia, J., Chen, J., Liu, S., Dong, W., Merbold, L., Law, B., Arain, A., Beringer, J., Bernhofer, C., Black, A., Blanken, P. D., Cescatti, A., Chen, Y., Francois, L., Gianelle, D., Janssens, I. A., Jung, M., Kato, T., Kiely, G., Liu, D., Marcolla, B., Montagnani, L., Raschi, A., Roupsard, O., Varlagin, A., and Wohlfahrt, G.: Global comparison of light use efficiency models for simulating terrestrial vegetation gross primary production based on the La Thuile database, Agr. Forest. Meteorol., 192, 108–120, https://doi.org/10.1016/j.agrformet.2014.03.007, 2014.
Yuan, W., Liu, S., Zhou, G., Zhou, G., Tieszen, L. L., Baldocchi, D., Bernhofer, C., Gholz, H., Goldstein, A. H., Goulden, M. L., Hollinger, D. Y., Hu, Y., Law, B. E., Stoy, P. C., Vesala, T., Wofsy, S. C., and other AmeriFlux collaborators: Deriving a light use efficiency model from eddy covariance flux data for predicting daily gross primary production across biomes, Agr. Forest. Meteorol., 143, 189–207, https://doi.org/10.1016/j.agrformet.2006.12.001, 2007.
Yuan, W., Luo, Y., Li, X., Liu, S., Yu, G., Zhou, T., Bahn, M., Black, A., Desai, A. R., Cescatti, A., Marcolla, B., Jacobs, C., Chen, J., Aurela, M., Bernhofer, C., Gielen, B., Bohrer, G., Cook, D. R., Dragoni, D., Dunn, A. L., Gianelle, D., Gruenwald, T., Ibrom, A., Leclerc, M. Y., Lindroth, A., Liu, H., Marchesini, L. B., Montagnani, L., Pita, G., Rodeghiero, M., Rodrigues, A., Starr, G., and Stoy, P. C.: Redefinition and global estimation of basal ecosystem respiration rate, Global Biogeochem. Cy., 25, GB4002, https://doi.org/10.1029/2011gb004150, 2011.
Yuan, W., Liu, S., Yu, G., Bonnefond, J.-M., Chen, J., Davis, K., Desai, A. R., Goldstein, A. H., Gianelle, D., Rossi, F., Suyker, A. E., and Verma, S. B.: Global estimates of evapotranspiration and gross primary production based on MODIS and global meteorology data, Remote Sens. Environ., 114, 1416–1431, https://doi.org/10.1016/j.rse.2010.01.022, 2010.
Yuan, W., Zheng, Y., Piao, S., Ciais, P., Lombardozzi, D., Wang, Y., Ryu, Y., Chen, G., Dong, W., Hu, Z., Jain, A.K., Jiang, C., Kato, E., Li, S., Lienert, S., Liu, S., Nabel, J. E. M. S., Qin, Z., Quine, T., Sitch, S., Smith, W. K., Wang, F., Wu, C., Xiao, Z., and Yang, S.: Increased atmospheric vapor pressure deficit reduces global vegetation growth, Sci. Adv., 5, eaax1396, https://doi.org/10.1126/sciadv.aax1396, 2019.
Zhang, H. Q., Pak, B., Wang, Y. P., Zhou, X. Y., Zhang, Y. Q., and Zhang, L.: Evaluating Surface Water Cycle Simulated by the Australian Community Land Surface Model (CABLE) across Different Spatial and Temporal Domains, J. Hydrometeorol., 14, 1119–1138, 2013.
Zhang, Y., Xiao, X., Wu, X., Zhou, S., Zhang, G., Qin, Y., and Dong, J.: Data Descriptor: A global moderate resolution dataset of gross primary production of vegetation for 2000–2016, Sci. Data, 4, 170165, https://doi.org/10.1038/sdata.2017.165, 2017.
Zhao, M. and Running, S. W.: Drought-Induced Reduction in Global Terrestrial Net Primary Production from 2000 Through 2009, Science, 329, 940–943, https://doi.org/10.1126/science.1192666, 2010.
Zheng, Y., Shen, R., Wang, Y., Li, X., Liu, S., Liang, S., Chen, J. M., Ju, W., Zhang, L., and Yuan, W.: Improved estimate of global gross primary production for reproducing its long-term variation, 1982–2017, figshare, Dataset, https://doi.org/10.6084/m9.figshare.8942336.v3, 2019.
Zheng, Y., Zhang, L., Xiao, J., Yuan, W., Yan, M., Li, T., and Zhang, Z.: Sources of uncertainty in gross primary productivity simulated by light use efficiency models: Model structure, parameters, input data, and spatial resolution, Agr. Forest. Meteorol., 263, 242–257, https://doi.org/10.1016/j.agrformet.2018.08.003, 2018.
Zhou, S., Williams, A. P., Berg, A. M., Cook, B. I., Zhang, Y., Hagemann, S., Lorenz, R., Seneviratne, S. I., and Gentine, P.: Land-atmosphere feedbacks exacerbate concurrent soil drought and atmospheric aridity, P. Natl. Acad. Sci. USA., 116, 18848–18853, 2019a.
Zhou, S., Zhang, Y., Williams, A. P., and Gentine, P.: Projected increases in intensity, frequency, and terrestrial carbon costs of compound drought and aridity events, Sci. Adv., 5, eaau5740, https://doi.org/10.1126/sciadv.aau5740, 2019b.
Zhu, Z., Piao, S., Myneni, R. B., Huang, M., Zeng, Z., Canadell, J. G., Ciais, P., Sitch, S., Friedlingstein, P., Arneth, A., Cao, C., Cheng, L., Kato, E., Koven, C., Li, Y., Lian, X., Liu, Y., Liu, R., Mao, J., Pan, Y., Peng, S., Penuelas, J., Poulter, B., Pugh, T. A. M., Stocker, B. D., Viovy, N., Wang, X., Wang, Y., Xiao, Z., Yang, H., Zaehle, S., and Zeng, N.: Greening of the Earth and its drivers, Nat. Clim. Change, 6, 791–796, https://doi.org/10.1038/nclimate3004, 2016.