Spatial and temporal patterns of global soil heterotrophic respiration in terrestrial ecosystems

Soil heterotrophic respiration (RH) is one of the largest and most uncertain components of the terrestrial carbon cycle, directly reflecting carbon loss from soils to the atmosphere. However, high variations and uncertainties of RH existing in global carbon cycling models require RH estimates from different angles, e.g., a data-driven angle. To fill this knowledge gap, this study applied a Random Forest (RF) algorithm (a machine learning approach) to (1) develop a globally gridded RH dataset and (2) investigate its spatial and temporal patterns from 1980 to 2016 at the global scale by linking field observations from the Global Soil Respiration Database and global environmental drivers (temperature, precipitation, soil water content, etc.). Finally, a globally gridded RH dataset was developed covering from 1980 to 2016 with a spatial resolution of half a degree and a temporal resolution of 1 year. Globally, the average annual RH was 57.2±0.6 Pg C a⁻¹ from 1980 to 2016, with a significantly increasing trend of 0.036±0.007 Pg C a⁻². However, the temporal trend of the carbon loss from RH varied in climate zones, and RH showed a significant and increasing trend in boreal and temperate areas. In contrast, such a trend was absent in tropical regions. Temperature-driven RH dominated 39 % of global land and was primarily distributed at high-latitude areas. The areas dominated by precipitation and soil water content were mainly semiarid and tropical areas, accounting for 36 % and 25 % of global land area, respectively, suggesting variations in the dominance of environmental controls on the spatial patterns of RH. The developed globally gridded RH dataset will further aid in the understanding of the mechanisms of global soil carbon dynamics, serving as a benchmark to constrain terrestrial biogeochemical models. The dataset is publicly available at https://doi.org/10.6084/m9.figshare.8882567 (Tang et al., 2019a).

1 Introduction

Global soils and surface litter store up to 2 or 3 times the amount of carbon present in the atmosphere (Trumbore, 2009), and therefore a small change in soil carbon content could have profound effects on atmospheric CO₂ and climate change (Köchy et al., 2015). Although global carbon flux from soil-to-atmosphere is increasing (Zhao et al., 2017), the degree to which future climate change will stimulate soil carbon loss via heterotrophic respiration (RH) remains highly uncertain (Bond-Lamberty et al., 2018; Friedlingstein et al., 2014; Trumbore and Czimczik, 2008), particularly for areas with a high temperature sensitivity or rapid changes in precipitation frequency and intensity.

Soil RH represents the carbon loss from the decomposition of litter detritus and soil organic matter by microorganisms (Subke et al., 2006), accounting for one of the largest components of the terrestrial carbon cycle (Bond-Lamberty et al., 2016). However, RH's feedback to climate variability is poorly understood. RH could affect future climate change via the mineralization of long-stored soil carbon, offsetting net primary production (NPP) and even converting terrestrial ecosystems from a carbon sink to a carbon source (Tremblay et al., 2018). Conversion of the sink or source role depends on how strongly large-scale processes are affected by environmental drivers, e.g., temperature, precipitation, and soil organic carbon content (Hursh et al., 2017; Sierra et al., 2015), or extreme conditions, e.g., fire, human disturbance, and drought (Kurz et al., 2013; Metsaranta et al., 2011). Although it is widely recognized that warming enhances CO₂ release from soils, the magnitude of such release is uncertain due to variations in the temperature sensitivity of soil organic matter decomposition (Suseela et al., 2012). In addition, environmental drivers of RH, e.g., temperature and soil moisture, are still undergoing changes under climate warming and can affect RH individually or interactively. Therefore, reducing RH uncertainty and clarifying the response of RH to environmental factors are both essential for future projections of the impact of climate change on the terrestrial carbon balance.

Due to the diurnal, seasonal and annual variability in RH, in addition to the difficulties of large-scale measurements, regional and global RH estimations mainly depend on modeling approaches using regional or global variables, such as temperature, precipitation and carbon supply (Bond-Lamberty and Thomson, 2010b; Hashimoto et al., 2015; Hursh et al., 2017). Besides temperature and precipitation, soil variables, such as water, carbon and nitrogen contents, are also important factors in the regulation of RH and should be considered for accurate RH estimations (Hursh et al., 2017; Zhao et al., 2017), although these variables vary with biome and climate.

Observational studies have examined the responses of soil respiration to different climatic variables at different locations across the globe (Bond-Lamberty and Thomson, 2010a; Zhou et al., 2016). Hashimoto et al. (2015) and Bond-Lamberty and Thomson (2010b) predicted global soil respiration rates using climate-derived models driven by temperature and precipitation; however, these models commonly explain less than 50 % of variations in soil respiration, requiring new techniques and potential new numerical and algorithmic methods to better quantify and understand the large-scale soil carbon fluxes (Bond-Lamberty, 2018). To improve modeling accuracy, more recent studies have used linear regression or machine learning approaches including more abiotic or biotic variables, such as soil carbon supply, soil properties and NPP (Hursh et al., 2017; Zhao et al., 2017), and observations collected from newly published measurements (Jian et al., 2018; Zhao et al., 2017). On the other hand, including more variables in linear or nonlinear regression models may cause overfitting and autocorrelation issues (Long and Freese, 2006). To overcome overfitting and autocorrelation, machine learning approaches, such as the Random Forest (RF, Breiman, 2001), have been applied to explore the hierarchical importance of environmental factors, such as temperature, soil water content (SWC), NPP and soil pH (Hursh et al., 2017). Machine learning techniques are highly effective because they are fully data adaptive, do not require initial assumptions on functional relationships and can function with nonlinear dependencies (Bodesheim et al., 2018). Therefore, these approaches are beginning to see use in Earth science, particularly in carbon and water flux modeling (Jung et al., 2010, 2017; Yao et al., 2018b), and may provide more reliable estimates of soil respiration (Bond-Lamberty, 2018; Zhao et al., 2017). However, no study to date has assessed the global variability of RH using empirical field observations to bridge the knowledge gap between local, regional and global scales.

The newly emerged Dynamic Global Vegetation Models from the TRENDY model ensembles and Earth System Models have been widely used to investigate major physiological and ecological processes and ecosystem structures, providing a novel database and approach to examine and estimate RH at the global scale (Zhu et al., 2017), although RH improvements in Earth System Models are still required (Shao et al., 2013). TRENDY and Earth System Model simulations incorporating a RH component are commonly calibrated and validated by eddy covariance measurements, e.g., net ecosystem carbon exchange; however, modeled RHs from these models have not yet been calibrated and validated using field observations. Therefore, these modeled RHs may be fundamentally different from observed values and no global observations exist to evaluate model effectiveness. Consequently, a data-driven RH dataset could improve our understanding of the underlying mechanisms of RH variability to climate change at the global scale and could serve as a benchmark to constrain terrestrial biogeochemical models.

Thus, we used a RF algorithm to estimate global RH based on updated RH observations from the Global Soil Respiration Dataset (SRDB, Bond-Lamberty and Thomson, 2010a) with the objectives of (1) developing a globally gridded RH product (named data-derived RH), (2) detecting the spatial and temporal patterns of RH, (3) identifying the dominant driving factors for spatial and temporal variabilities of RH, and (4) comparing the data-derived RH dataset with RH generated by Dynamic Global Vegetation Models from the TRENDY ensembles.

2 Materials and methods

2.1 Soil heterotrophic respiration database development

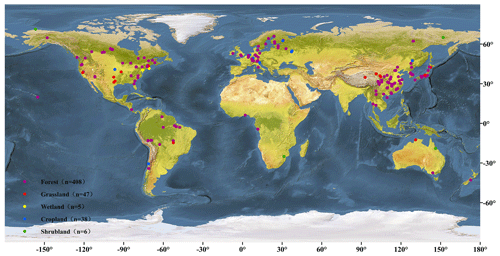
The basis of the database developed here included observed global RH values from SRDB (Bond-Lamberty and Thomson, 2010a), which were freely obtained at https://github.com/bpbond/srdb (last access: January 2018). The database was further updated using observations collected from peer-reviewed Chinese publications at the China Knowledge Resource Integrated Database (https://www.cnki.net/, last access: March 2018) until March 2018. This study included the RH data for (1) annual RH, as directly reported in publications with at least 1 year continuous measurements, and (2) the start and end years extracted from SRDB, directly from publications, or calculated by the “years of data” in the SRDB. (3) Observations measured by alkali absorption or soda lime approaches were not included because of their potential underestimation of respiration flux with increasing pressure in the measurement chamber (Pumpanen et al., 2004). (4) Experiments with treatments, such as nitrogen manipulation or fertilization were excluded, and only RH measurements from the control treatment were included (Jian et al., 2018). (5) SRDB observations labeled as “potential problem” (Q10), “suspected problem” (Q11), “known problem” (Q12), “duplicate” (Q13) and “inconsistency” (Q14) were not included (Bond-Lamberty and Thomson, 2010a). In total, the newly updated database included 504 RH observations in total. Although most of the observations were from China, North America, South America and Europe, this database covered all of the major terrestrial biomes across the world (Fig. 1).

Figure 1 Distributions of the study sites for RH observations.

2.2 Climate and soil data

To investigate the global spatial and temporal RH patterns, global spatial–temporal grids of RH driving factors were required. A total of nine global variables were included (Table S1): monthly gridded data of temperature, precipitation, diurnal temperature range from Climatic Research Unit TS v.4.01 over 1901–2016 (https://crudata.uea.ac.uk, last access: September 2017, Harris et al., 2014); shortwave radiation (SWR, https://www.esrl.noaa.gov, last access: March 2018, Kalnay et al., 1996); gridded soil organic carbon content (Hengl et al., 2017) and nitrogen content from https://webmap.ornl.gov/ogc/index.jsp, last access: March 2018, (Global Soil Data, 2000); monthly gridded nitrogen deposition dataset from the global Earth System Models of GISS-E2-R, CCSM-CAM3.5 and GFDL-AM3 from 1850 to the 2000s (https://www.isimip.org, last access: June 2017, Lamarque et al., 2013); monthly Palmer Drought Severity Index data (PDSI, https://www.esrl.noaa.gov/psd/, last access: October 2017, Dai et al., 2004) and soil water content (SWC, https://www.esrl.noaa.gov, last access: March 2018, van den Dool et al., 2003). Before further data analysis, monthly data were aggregated to an annual scale. These variables could stand for different environmental controls on RH. For example, temperature, precipitation and SWC are critical environmental controls on microbial activities for soil organic matter decomposition (Jian et al., 2018; Suseela et al., 2012; Tremblay et al., 2018). Soil organic matter, soil carbon stock and soil nitrogen are important carbon and nitrogen substrates for microbes that are related to the decomposition of soil organic matter (Tremblay et al., 2018). The drought index (PDSI) and diurnal temperature range represent water and temperature stress on RH (Berryman et al., 2015; Zhu and Cheng, 2011). The global environmental drivers for each given site were extracted by site longitudes and latitudes corresponding to annual RH observations. If the environmental driver is not in a spatial resolution of 0.5^∘, we first resampled this environmental driver to a 0.5^∘ resolution using the bilinear interpolation.

2.3 RH from TRENDY models

Over the last several decades, TRENDY models were developed to simulate key processes (e.g., photosynthesis, respiration, evapotranspiration, phenology and carbon allocation) that drive the dynamics of global terrestrial ecosystems (Piao et al., 2015). TRENDY models follow a common protocol and use the same climate-forcing data from National Centers for Environmental Prediction at a spatial resolution of 0.5^∘. For modeled products with different spatial resolutions, new errors will be produced when resampling to 0.5^∘. Therefore, to compare the dynamics in the data-derived RH dataset and TRENDY RH dataset, we used model outputs from seven TRENDY models: Community Land Model 4.5 (CLM4, Lawrence et al., 2011), Integrated Science Assessment Model (ISAM, Cao, 2005), Lund-Potsdam-Jena (LPJ, Sitch et al., 2003), Lund-Potsdam-Jena General Ecosystem Simulator (LPJ-GUESS, Smith et al., 2001), VEgetation-Global-Atmosphere-Soil (VEGAS, Zeng et al., 2005), and Vegetation Integrative Simulator for Trace gases (VISIT, Kato et al., 2013). Additionally, the RH dataset generated empirically by Hashimoto et al. (2015) was compared (denoted as Hashimoto RH), which is publicly available (http://cse.ffpri.affrc.go.jp/shojih/data/index.html, last access: January 2018) and estimated from a global relationship between RH and soil respiration (Bond-Lamberty et al., 2004), and the total soil respiration was predicted from a climate-driven model using precipitation and temperature based on the observations from SRDB. More details can be found in Hashimoto et al. (2015).

2.4 RF-based RH modeling

RF is a machine learning approach that uses a large number of ensemble regression trees with a random selection of predictive variables (Breiman, 2001). Two free parameter settings are required, which are the number of trees and candidate variables for each split. However, the RF model is not usually sensitive to the number of trees or variables. A RF regression can deal with a large number of features, assisting a feature selection based on the importance value of each variable and the avoidance of overfitting (Bodesheim et al., 2018; Jian et al., 2018). In the present study, a RF model was trained using nine variables (Table S1) in the caret package (version 6.0-80, accessed on 27 May 2018) in R (R Core Team, 2018), which was then implemented to predict RH for each grid at a spatial resolution of 0.5^∘. To characterize the performance of RF, a 10-fold cross-validation was applied, which meant that the dataset was stratified into 10 parts, and each part contained a roughly equal number of samples. The target values for each of these 10 parts were predicted based on the training models using the remaining 9 parts. Two model evaluation statistics were used, including modeling efficiency (R²) and root-mean-square error (RMSE, Tang et al., 2019b; Yao et al., 2018b).

2.5 Trend analysis

A trend analysis of RH was estimated using the Theil–Sen linear regression and tested with the Mann–Kendall nonparametric test. The Theil-Sen estimator is a nonparametric slope estimator based on median values, and this approach was widely used for time series analysis, e.g., carbon fluxes (Dai et al., 2016) and vegetation greening and browning (Pan et al., 2018). The Mann–Kendall nonparametric test was employed to investigate the significant changes in RH trend at a significance level of 0.05.

2.6 Relationships between RH and temperature, precipitation and SWC

Although previous studies have used precipitation as a proxy for SWC (Bond-Lamberty and Thomson, 2010b; Chen et al., 2010), this may result in variability in soil respiration estimates (Jassal et al., 2007; Zhang et al., 2006) because the relationship between SWC and soil respiration was much more complex than that between soil respiration and temperature or precipitation (Jian et al., 2018). Therefore, mean annual temperature (MAT), precipitation (MAP) and SWC were all considered potentially important proxies driving RH (Bond-Lamberty et al., 2016; Reichstein and Beer, 2008). Annual mean RH was regressed against the three proxies. The relationships between the data-derived RH and MAT, MAP, and SWC were assessed locally for each grid cell by calculating the correlations using partial correlation analysis. When analyzing the partial correlations between RH and the proxy, the other two proxies were controlled to remove their confounding effects on RH. The correlation strengths of MAT, MAP and SWC were used to derive RGB combinations and indicate the drivers of RH.

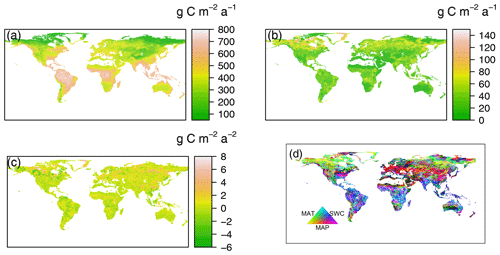
Figure 2 Spatial patterns of (a) mean data-derived RH, (b) standard deviations, (c) temporal trends of annual heterotrophic respiration (RH) from 1980 to 2016 and (d) dominant environmental drivers for the interannual variability of global RH. MAT is mean annual temperature, MAP is mean annual precipitation and SWC is soil water content.

2.7 The comparison map profile method

To detect the spatial similarity and difference patterns between the data-derived RH and TRENDY and Hashimoto RH values from 1981 to 2010, we utilized the comparison map profile (CMP) method (Gaucherel et al., 2008). This method was based on the absolute distances (D) and cross-correlation coefficients (CC) across multiple scales, with D and CC reflecting the similarity and the spatial structures of two compared images with the same sizes, respectively (Gaucherel et al., 2008). The D value between moving windows (from 3×3 to 1×41 pixels in present study) of two compared images was calculated by Eq. (1):

$$\begin{array}{}\text{(1)}& D=\text{abs}(\stackrel{\mathrm{‾}}{x}-\stackrel{\mathrm{‾}}{y}),\end{array}$$

where $\stackrel{\mathrm{‾}}{x}$ and $\stackrel{\mathrm{‾}}{y}$ represent mean values calculated over two moving windows. Finally, the mean D value was calculated as an average of different moving windows.

The CC was calculated according to Eq. (2):

$$\begin{array}{}\text{(2)}& \mathrm{CC}={\displaystyle \frac{\mathrm{1}}{N^{\mathrm{2}}}}\sum _{i=\mathrm{1}}^N\sum _{j=\mathrm{1}}^N{\displaystyle \frac{(x_{ij}-\stackrel{\mathrm{‾}}{x})\times (y_{ij}-\stackrel{\mathrm{‾}}{y})}{{\mathit{\sigma }}_x\times {\mathit{\sigma }}_y}},\end{array}$$

$$\begin{array}{}\text{(3)}& {\mathit{\sigma }}_x^{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{N^{\mathrm{2}}-\mathrm{1}}}\sum _{i=\mathrm{1}}^N\sum _{j=\mathrm{1}}^N(x_{ij}-\stackrel{\mathrm{‾}}{x}{)}^{\mathrm{2}},\end{array}$$

where x_ij and y_ij are pixel values at the ith row and jth column of the moving windows of two compared images, respectively. N represents the total number of pixels covered by each of moving windows. σ_x and σ_y stand for standard deviations of two moving windows. Low D values reflect a goodness of fit between the compared images, while low CC values suggest a low similarity. Finally, the mean D and CC were calculated as the average from different moving windows.

All data analyses mentioned above were conducted in R (version 3.5.0, access on April 2018).

3 Results

3.1 Spatial patterns of RH

Based on the 10-fold cross-validation, R² and RMSE were 50 % and 143 g C m⁻² a⁻¹ (Fig. S1), respectively. This indicates that the RF algorithm effectively captured the spatial and temporal variability of RH, therefore enabling derivation of a global gridded RH dataset.

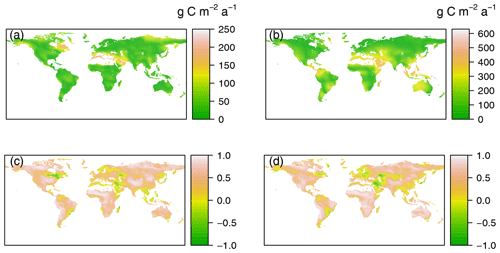
Figure 3 Comparing the data-derived RH dataset with Hashimoto RH (a, c) and mean RH of TRENDY models (b, d) based on absolute distances (g C m⁻² a⁻¹, a, b) and cross-correlations (c, d). The absolute distances and cross-correlations were calculated using comparison map profile method (Gaucherel et al., 2008).

The data-derived RH dataset showed a strong spatial pattern globally (Fig. 2a). The largest RH fluxes occurred in tropical areas, e.g., Amazonian tropical forests, at > 700 g C m⁻² a⁻¹; followed by the subtropics, e.g., southern China and America; and humid temperate areas, e.g., North America and western and central Europe, with an annual RH of 400–600 g C m⁻² a⁻¹. Relatively low annual RH of less than 200 g C m⁻² a⁻¹ was generally observed in areas with cold and dry climates, such as boreal areas, characterized by low temperatures and short growing seasons and dry or semiarid regions (e.g., northwestern China), where water availability limits ecosystem development. However, the most variable changes in RH over the time from 1980 to 2016, using standard deviation and coefficient of variation (CV, the ratio of the standard deviation and the mean) as a proxy (Figs. 2b and S3), were found in boreal regions with RH higher than 70 g C m⁻² a⁻¹ or a CV > 0.7. The majority of areas of RH variabilities were lower than 30 g C m⁻² a⁻¹ or a CV < 0.3. Similarly, TRENDY RH showed similar patterns, with the highest RH in warm and humid areas and the lowest RH in cold and dry regions (Fig. S2). However, differences existed in the absolute RH fluxes (Fig. S2). For example, CLM4 and VISIT models predicted RH to be higher than 1400 g C m⁻² a⁻¹ within Amazon forest regions, while ISAM and LPJ-GUESS estimates were typically low at around 1000 g C m⁻² a⁻¹. However, the data-derived RH dataset and Hashimoto RH showed the highest RH fluxes in tropical regions of about 800 g C m⁻² a⁻¹.

To examine the similarity in the patterns between the data-derived RH dataset and TRENDY–Hashimoto RH, the CMP method was employed (Fig. 3). Larger D and lower CC values indicate less consistent magnitudes and a local gradient distributions between the two compared images. The data-derived RH dataset and Hashimoto RH differed greatly in eastern Canada and the Middle East with D values higher 200 g C m⁻² a⁻¹ and CC values lower than −0.5. Interestingly, the most noticeable differences between the data-derived RH and mean TRENDY RH occurred in East Asia and the Middle East, where D was higher than 500 g C m⁻² a⁻¹, while CCs were around −0.1. When assessing each TRENDY model individually (Figs. S4 and S5), the differences between the data-derived RH dataset and TRENDY RH were even larger. The most remarkable differences were found for CLM4 and VISIT models in regions where D was above 800 g C m⁻² a⁻¹ with CC values of about −0.3 (East Asia and America).

Across the latitudinal gradients, zonal mean RH values increased from cold or dry areas (e.g., tundra, and desert or semiarid areas) to warm or humid areas (e.g., temperate and tropical areas, Fig. S6). The data-derived RH dataset varied from 60±12 at about 75^∘ N to 640±71 g C m⁻² a⁻¹ at the Equator, reflecting higher resource limitation in high-latitude areas and lower resource limitation in low-latitude areas. In the dry tropical areas (10–25^∘ S and 10–25^∘ N) limited by water, the zonal mean RH decreased slightly. With the increase in water availability, RH showed a second peak in the Northern and Southern hemispheres around 20^∘ N and 40^∘ S, respectively. Nonetheless, there was a high level of variability between the data-derived RH and TRENDY–Hashimoto RH in equatorial regions (Fig. S6), with predictions generally overestimating RH at the Equator. Peak RH values in the equatorial region ranged from 660±65 g C m⁻² a⁻¹ for ORCHIDEE model to above 1200±460 g C m⁻² a⁻¹ for the CLM4 model, resulting in a considerably higher peak RH value for the model mean (950±300 g C m⁻² a⁻¹).

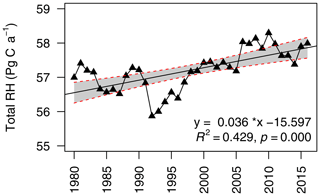
Figure 4 Interannual changes in global heterotrophic respiration (RH) from 1980 to 2016. The grey area indicates 95 % confidence intervals. For the linear regression model, R²=0.429 and p<0.01.

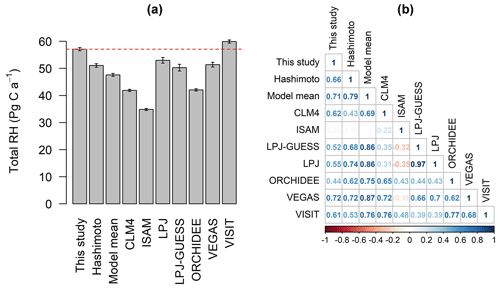
Figure 5 (a) Total global heterotrophic respiration (RH, mean ± standard deviation of annual RH from 1981 to 2010) fluxes and (b) the correlation coefficient analyzed by Pearson correlation between data-derived RH and TRENDY–Hashimoto RH. The dashed red line in (a) represents the average of data-derived RH from 1981 to 2010.

3.2 Total RH

Over the last 37 years, the global RH has increased from 55.8 Pg C a⁻¹ (1 Pg $=\mathrm{1}\times {\mathrm{10}}^{\mathrm{15}}$ g) in 1992 to 58.3 Pg C a⁻¹ in 2010, with an average of 57.2±0.6 Pg C a⁻¹ and strong annual variabilities (Fig. 4). Compared to the data-derived RH dataset, TRENDY–Hashimoto RH was underestimated (Fig. 5a), with the exception of the VISIT model. ISAM predicted the lowest global RH of 34.8±0.4 Pg C a⁻¹, while the VISIT model produced the highest RH of 59.9±0.6 Pg C a⁻¹ (Fig. 5a). The model mean RH was 47.6±0.5 Pg C a⁻¹, underestimating RH by 9.6 Pg C a⁻¹ (16 %) in comparison to the data-derived RH dataset. Due to this large divergence, the strength of correlation between the data-derived RH and TRENDY–Hashimoto RH varied greatly from 0.06 to 0.72 (Fig. 5b). Boreal, temperate and tropical regions were the three most important contributors for the global RH according to the Köppen–Geiger climate classification system (Peel et al., 2007), contributing 76 % of the total global RH. The mean RH of boreal, temperate and tropical areas were 10.8±0.3, 12.9±0.1 and 19.5±0.2 Pg C a⁻¹, accounting for 19 %, 22 % and 35 % of the total global RH, respectively (Fig. S8).

3.3 Trends in RH

Globally, although there was a great interannual variability in RH, the total RH has significantly increased at a rate of 0.036±0.007 Pg C a⁻² from 1980 to 2016 (p=0.000, Fig. 4). Comparison of the data-derived RH dataset and TRENDY RH during the period of 1981 to 2010 was performed. The data-derived RH increased at 0.041±0.01 Pg C a⁻² (Fig. S7), which was lower than that of TRENDY RH (0.057±0.009 Pg C a⁻²) and Hashimoto RH (0.057±0.009 Pg C a⁻²). Additionally, temporal trends varied greatly among TRENDY models (Fig. S7), with the largest increasing trend of 0.123±0.013 Pg C a⁻² for LPJ-GUESS and the largest decreasing trend of $-\mathrm{0.018}\pm \mathrm{0.007}$ Pg C a⁻² for ISAM.

Temporal trends varied among climate zones. RH in boreal and temperate areas increased by 0.020±0.004 and 0.007±0.002 Pg C a⁻² from 1980 to 2016 (p < 0.001, Fig. S8), respectively, while RH in tropical areas did not show a significant temporal trend, although interannual variabilities were observed (p=0.362, Fig. S8). TRENDY–Hashimoto RHs showed significant increasing temporal trends in boreal, temperate and tropical regions, except in the ISAM and ORCHIDEE models (Figs. S9–11). However, the increasing magnitude varied among different TRENDY models.

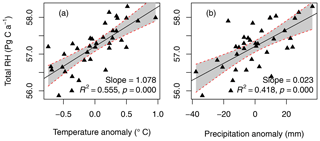
From 1980 to 2016, the global RH was expected to be driven by multiple environmental factors, such as temperature and precipitation. During this period, MAT and MAP levels increased significantly by 0.34±0.032 ^∘C and 6.69±2.399 mm per decade, respectively (p<0.01, Fig. S12a and b). Therefore, the correlations between RH and MAT and MAP were evaluated. Globally, RH was significantly correlated with MAT (R²=0.56, p<0.001) and MAP (R²=0.42, p<0.001, Fig. 6) anomalies. On average, the global RH increased by 1.08±0.163 Pg C a⁻¹ per 1 ^∘C increase in MAT and 0.23±0.046 Pg C a⁻¹ per 10 mm increment in MAP.

Figure 6 The relationships between heterotrophic respiration (RH) and mean annual temperature (a) or precipitation anomalies (b). The change was calculated as the difference of each given year to the average over 1980 to 2016. Grey areas indicate 95 % confidence intervals.

3.4 Spatial pattern of RH trends

Spatially, the data-derived RH trends presented heterogeneous geographical patterns (Fig. 2c). Positively increasing trends of RH were found for more than half of the global land areas (59 %, calculated from cell areas; Fig. S13). Generally, the increasing rates of RH were lower than 3 g C m⁻² a⁻². In contrast, the highest RH increase was above 6 g C m⁻² a⁻² in boreal regions, such as Russia, northern Canada and the Tibetan Plateau. RH exhibited a decreasing trend in 41 % of the global land area and most considerably in South Asia (Fig. 2c). Similar to the data-derived RH trends, RH trends estimated by the TRENDY–Hashimoto RH trend also showed heterogeneous geographical patterns (Fig. S14). However, large discrepancies were found among TRENDY–Hashimoto RH (Figs. 2c and S14). Generally, the largest increase in RH trends occurred in boreal areas, except for outputs by LPJ-GUESS and LPJ models, which showed a decreasing trend for most boreal areas. There was a decreasing trend across most of the tropics (e.g., Southeast Asia), with the exception of VEGAS model (Fig. S14).

3.5 Dominant factors in RH annual variability

MAT and MAP were the most important factors dominating RH in 39 % and 36 % of global land areas, respectively (Fig. S15), while SWC dominated the remaining 25 % of global land areas. Spatially, the dominant drivers controlling RH varied greatly across the globe (Fig. 2d), with the area dominated by temperature mainly distributed in boreal areas above 50^∘ N. This was also observed in the relatively high and positive partial correlation coefficient between temperature and RH (Fig. S15a). In contrast, precipitation dominated temperate areas between 25 and 50^∘ N (such as northern China, the Middle East and America), where a wide distribution of desert or semiarid regions occur, SWC dominated in tropical areas, such the Amazon, India and Africa. Similarly, water availability (SWC and precipitation) were also main driving factors for RH in Australia.

Spatial patterns in environmental controls on TRENDY–Hashimoto RH varied greatly compared to the data-derived RH dataset or among TRENDY models (Figs. 2d and S15–17). Water availability (including precipitation and SWC) appeared to be more important than temperature. The percentage of the areas dominated by temperature (mainly distributed in boreal areas, except for in ISAM model outputs) was less than the areas dominated by precipitation and SWC (globally distributed) (Fig. S17). In terms of the mean TRENDY RH, precipitation dominated most of global land areas (43 %), followed by SWC (36 %) and temperature (21 %) (Fig. S15).

4 Discussion

4.1 Annual RH

4.1.1 Comparison with Hashimoto RH

Despite increasing efforts to quantify the global carbon cycle, large uncertainties still remain in the spatial and temporal patterns in RH. To the best of our knowledge, this is the first study to apply the RF approach to predict the spatial and temporal patterns of global RH using field observations. Globally, the mean RH amounted to 57.2±0.6 Pg C a⁻¹ from 1980 to 2016, 13.6 Pg C a⁻¹ higher than RH from a satellite-driven estimate (Konings et al., 2019) and 6.4 Pg C a⁻¹ higher than Hashimoto RH (Hashimoto et al., 2015). The differences between the data-driven RH and Hashimoto may be due to several reasons. Firstly, the two RH products covered different land areas, with the data-derived RH dataset covering a higher land area. If the data-derived RH dataset was masked by Hashimoto RH over 1981–2010, the total RH was 51.8±0.6 Pg C a⁻¹, close to that of Hashimoto RH with 51.1±0.7 Pg C a⁻¹ (Fig. S18). However, the spatial and temporal patterns varied greatly (Figs. 3 and 5).

Secondly, the two RH products used different variables and algorithms for RH predictions. RH was not only affected by temperature and precipitation but also by carbon substrates, soil nutrient levels and other variables (Hursh et al., 2017). Besides temperature and precipitation, we also included SWC, soil nitrogen and carbon contents as indicators for environmental and nutrient constraints on RH. Conversely, Hashimoto RH was estimated from a climate-driven model including only temperature and precipitation as the driving variables (Hashimoto et al., 2015). This simple model can partly explain the reasons that Hashimoto RH could not capture the significant decrease in RH in 1982 and 1991 due to the El Chichón and Pinatubo eruptions, respectively (Zhu et al., 2016), while the data-derived RH dataset and TRENDY RH successfully captured such effects.

Thirdly, the linear model between total soil respiration and RH was developed based on forest ecosystems (Bond-Lamberty et al., 2004; Hashimoto et al., 2015), which could be another uncertainty when applying this linear model to other ecosystems, e.g., croplands and grasslands.

4.1.2 Comparison with TRENDY models

As the data-derived RH dataset often serves as a benchmark for terrestrial biogeochemical models, the data-derived RH dataset was compared with TRENDY models from 1980 to 2010. Although the data-derived RH dataset lay within the model range (34.8±0.4 Pg C a⁻¹ for ISAM to 59.9±0.6 Pg C a⁻¹ for VISIT, Fig. 5a), the mean TRENDY RH was underestimated by 16 % compared to the data-derived RH dataset. Due to the different temporal trends among TRENDY models and their low spatial correlations to the data-derived RH dataset (correlation efficiencies ranging from 0.06 to 0.72, Fig. 6b), TRENDY RHs clearly have different sensitivities to climate variations. Additionally, the difference in RH magnitude and spatial pattern varied considerably, as shown by analysis of absolute distances and cross-correlations. This effect was mostly notable in tropical areas in VISIT and CLM4 models (Figs. S4 and S5). This phenomenon may be associated with several factors. Firstly, plant functional types differed among TRENDY models. For example, the VEGAS model included 4 plant functional types (Zeng et al., 2005), while the LPJ model defined 10 plant functional types (Sitch et al., 2003).

Secondly, for each set of equations, constant vegetation parameters (e.g., photosynthetic capacity) were applied across time and space for most TRENDY models, which may induce an RH bias. Model parameters using short-term observations do not account for the interannual variability of climatic and soil conditions, generating a simplistic representation of RH due to its inability to capture the response of RH to new environmental controls in short-term observations.

Thirdly, models that do not consider nitrogen constraint could overestimate the increasing trend of RH because nitrogen limitation was globally observed (LeBauer and Treseder, 2008). This could explain why the CLM4 model with a nitrogen constraint produced a much smaller increasing trend compared to other TRENDY models, with the exception of ISAM (Fig. S7). Therefore, including soil nitrogen as a driving variable in modeling RH in this dataset had the advantage of detecting the nitrogen constraints on RH.

Fourthly, the lack of the representation of human activities and agricultural management (e.g., fertilization and irrigation) may underestimate RH because fertilization and irrigation were important practices to increase RH (Chen et al., 2018; Zhou et al., 2016). This could explain why five of seven TRENDY models could not explain the significant increasing change of RH in central China (Fig. S14), which experienced an intensive use of fertilization for food security in recent decades.

Finally, uncertainties and differences in model structures could also lead to inconclusive RH estimations. Although the same climatic data, e.g., temperature and precipitation, were used for TRENDY models to reduce the uncertainty caused by various meteorological forcings, systematic errors may be caused by applying a particular forcing, and the errors might be propagated to model outputs (Anav et al., 2015). Therefore, TRENDY models should be improved by incorporating more processes such as nutrient constrains and an assessment of the model response to environmental variability (Keenan et al., 2012; Wang et al., 2014; Yao et al., 2018b).

4.2 Linkage to global carbon balance

Assuming that the global ratio of RH ∕ total soil respiration ranged from 0.56 (Hashimoto et al., 2015) to 0.63 (Bond-Lamberty et al., 2018), annual soil respiration varied from 90.8 to 102.1 Pg C a⁻¹, within the reported values of 83 to 108 Pg C a⁻¹ based on recent studies (Bond-Lamberty and Thomson, 2010b; Hursh et al., 2017). This indirectly highlights the reliability of the use of RF for global RH prediction. Moreover, these findings also have important indications of carbon balance estimations. According to a recent NPP estimate from observations and IPCC report data (IPCC, 2013; Li et al., 2017), the global NPP ranged from 61.5 to 60 Pg C a⁻¹, respectively. The residual between RH and NPP (net ecosystem production) was 2.8–4.3 Pg C a⁻¹, which is similar to the global estimates of net ecosystem production from the International Geosphere-Biosphere Programme, which ranged from 1.9 to 4.1 Pg C a⁻¹ from 1959 to 2016 (Le Quéré et al., 2013, 2016, 2014). With a 1 ^∘C increase in global MAT, RH will increase by 1.08 Pg C a⁻¹ globally, and such an increase is 0.23 Pg C a⁻¹ for a 10 mm increment in global MAP. These findings indicate that carbon fluxes from the decomposition of soil organic matter and litter (RH) may positively feedback to global climate change – typically characterized by increasing temperature and the changes in precipitation (IPCC, 2013).

4.3 Dominant factors in RH

Dominant factors driving RH varied spatially. As temperature and energy were the most limited climatic factors in high-latitude areas, temperature was a dominant factor for RH in high-latitude regions above 50^∘ N (Fig. 2d), with low temperatures leading to low RH (Fig. 2a). Similarly, due to the limited amount of precipitation, RH in semiarid areas was mainly controlled by precipitation, which was consistent with both reported field observations (Bai et al., 2008) and modeling studies (Gerten et al., 2008). SWC control of RH in tropical areas could be explained by the mechanisms of RH. Excessively high SWC can reduce the diffusion of oxygen, while excessively low SWCs could limit water and soluble substrate availabilities, preventing microbial activities (Luo and Zhou, 2006; Xu et al., 2004). Suseela et al. (2012) proposed that RH fluxes declined sharply when volumetric soil moisture reduced below ∼ 15 % or exceeded ∼ 26 %, which supported the findings of the present study. However, it should be noted that dominant environmental controls on spatial carbon flux gradients might vary among different years (Reichstein et al., 2007), such as with climatic extremes.

4.4 Temporal variability of tropical, temperate and boreal areas

RH in tropical areas did not exhibit a significant temporal pattern between 1981 and 2010 (Fig. S8, p=0.362), indicating that in our model climate change did not affect RH fluxes in these areas. However, RH in boreal and temperature areas experienced significant increasing trends of 0.020±0.004 and 0.007±0.002 Pg C a⁻², respectively (Fig. S7), suggesting that a positive feedback may occur with climate change. Tremblay et al. (2018) proposed that the increased RH was mainly related to the increasing temperature in boreal forest soils, which supported the findings of the present study. It should be noted that both the data-derived RH dataset and Hashimoto/TRENDY RH in boreal areas showed a temporally increasing trend from 1981 to 2010, although the magnitude of increase differed (Fig. S9). Furthermore, despite the ISAM model showing a decreasing trend for temperate and tropical regions, the ISAM model had an increasing trend in RH from 1981 to 2010 in boreal areas (Fig. S9). These results indicate that boreal regions are becoming increasingly important in global carbon cycling and that the increasing trend may continue due to a large amount of carbon stored in soils. Therefore, climate change may fundamentally alter carbon cycling in boreal areas through changes in the decomposition rate of soil organic matter (Crowther et al., 2016; Hashimoto et al., 2015; Schuur et al., 2015). Furthermore, the response of RH to climate variability varied with climate zone, indicating that different carbon loss rates from RH will occur in different regions to climate change.

4.5 Advantages, limitations and uncertainties

Based on the updated SRDB database, we used a RF algorithm to predict the spatial and temporal patterns of RH at the global scale and its response to environmental variables, and the data-derived RH could serve as a benchmark for terrestrial biogeochemical models and reduce RH uncertainties. This data-derived RH dataset provided several advantages to the estimation of global RH compared to previous studies, e.g., Hashimoto et al. (2015) and Konings et al. (2019). Firstly, we compiled up-to-date field observations from SRDB and peer-reviewed Chinese literatures up to March 2018, including 504 observations in total covering the majority global terrestrial ecosystems and climate zones (Fig. 1). Secondly, total RH and its interannual variability were assessed for boreal, temperate and tropical zones, i.e., the three main global climate zones. Analysis from the data-derived RH dataset further concluded that RH in different climate zones responded differently to global climate change. Thirdly, we applied the RF to predict and map RH at the global scale using climate and soil predictors. Compared to the linear regression analysis for predicting soil respiration (as no such global RH predictions were previously available for comparison) with model efficiencies of < 50 % (Bond-Lamberty and Thomson, 2010b; Hashimoto et al., 2015; Hursh et al., 2017), the RF algorithm achieved a higher model efficiency of 50 %. In addition to a feature selection according the importance value of each variable and avoiding overfitting (Bodesheim et al., 2018; Jian et al., 2018), the RF algorithm improved RH modeling accuracies and reduced uncertainties. Meanwhile, the data-derived RH dataset was cross-validated globally by a 10-fold cross-validation (see Sect. 2), which could improve its reliability and feasibility compared to TRENDY-based RH that was not validated and calibrated by field observations, bridging the knowledge gap between local, regional and global scales temporally and spatially with a large number of empirical field measurements.

However, although the data-derived RH dataset could be used as a benchmark for the verification of global carbon cycle modeling, bridging the knowledge gaps between local, regional and global scales, a few uncertainties and limitations still remain. Firstly, the RF algorithm constructed a model based on the training dataset and was typically data-limited in terms of quantity, quality and representativeness. Uneven data distribution has been a known issue in many ecological studies across the world, e.g., Bond-Lamberty and Thomson (2010b), Jung et al. (2011), Xu and Shang (2016), and Yao et al. (2018a). The RH observations were mainly from China, Europe and North America, while there were a lack of RH observations in Russia, Africa, Australia and southwestern Asia in our study. Thus, the uneven coverage of the observations was an important source of uncertainty to develop the data-derived RH dataset, which may cause a bias in the RF model towards the areas with more observations. However, our dataset covered a large climatic and edaphic gradient covering the major land covers and climate zones. Therefore, in future studies, increasing field observations in unsampled areas should greatly improve our ability to evaluate spatial and temporal patterns of RH at the global scale and model the global carbon cycle of climate change.

Secondly, the misrepresentation of human activities, particularly regarding land management and land use change, could result in uncertainties in RH (Bond-Lamberty et al., 2016; Tang et al., 2016). These human activities include both site-level in situ information and the corresponding global grids. Otherwise, such information must not have been included, as the corresponding site information or globally gridded datasets are missing or insufficient. Although soil organic carbon stock, soil nitrogen content, SWC and shortwave radiation were selected as inputs for the development of the RF model, which could partly capture land use change, the impacts of land use change on the interannual variability of RH have not been fully qualified in the present study. Therefore, further efforts are required to characterize and quantify the effects of land use change on the global RH.

Thirdly, the data-derived RH dataset was derived at an annual timescale, which may cause an additional uncertainty regarding the interannual variability of RH. Therefore, the needs for a larger number of global observations and to develop finer-scale temporal dynamics need further exploration, in combination with remote-sensing measurements and field observations, which may provide new insights into terrestrial ecosystem carbon dynamics at the global scale. Aside from this, without consideration of the temporal changes of soil organic carbon content from 1980 to 2016, this might be another uncertainty because the increase in productivity driven by CO₂ fertilization would increase litter input into soils. However, there is a lack of global soil organic carbon content product that considers its temporal changes based on observations.

Finally, we developed a global RH at a half-degree spatial resolution, which included a scale mismatch between the observations and global gridded variables. This could be a great challenge for spatial modeling and using global gridded variables with a finer resolution is encouraged to overcome this limitation (Xu and Shang, 2016). On the other hand, the study sites were globally distributed and there was a large climatic and edaphic gradient covering the major land covers and biomes, which should reflect a larger variability than the site-to-grid mismatch.

5 Data availability

The developed globally gridded RH database, the field RH observation dataset and R codes used to produce the main results are free to the public for scientific purposes and can be downloaded at https://doi.org/10.6084/m9.figshare.8882567 (Tang et al., 2019a).

6 Conclusions

A data-derived global RH dataset may be used as a benchmark for terrestrial biogeochemical models; however, no such study has yet been conducted to assess the global variability in RH using a large dataset of empirical measurements to bridge the knowledge gap between local, regional and global scales. To fill this knowledge gap, we developed a globally gridded RH dataset, which was $\mathrm{0.5}{}^{\circ }\times \mathrm{0.5}{}^{\circ }$ from 1980 to 2016 with an annually temporal resolution, using a RF algorithm by linking field observations and global variables. Our robust conclusions are as follows. (1) Annual mean RH was 57.2±0.6 Pg C a⁻¹ between 1980 and 2016, with an increasing trend of 0.036±0.007 Pg C a⁻², indicating an increase in carbon loss from soils to the atmosphere. (2) Significant temporal trends were observed in the RH in boreal and temperate areas, although none were found in tropical regions. This indicates that the temporal trend in RH varied with climate zone, highlighting their different sensitivities to climate change. (3) The magnitude and dominant factors of the data-derived TRENDY RH varied greatly, indicating that future efforts should focus on improving the representation of RH and its response to environmental variability in terrestrial biogeochemical models. (4) More field observations are required in areas with limited observational datasets, with the integration of smaller-scale temporal dynamics (rather than annual timescales) potentially providing new insights into terrestrial ecosystem carbon dynamics at the global scale. (5) The data-derived RH dataset could serve as a benchmark to constrain the terrestrial biogeochemical models, further contributing to improving our understanding of the mechanisms of global soil carbon dynamics.