Using CALIOP to estimate cloud-field base height and its uncertainty: the Cloud Base Altitude Spatial Extrapolator (CBASE) algorithm and dataset

A technique is presented that uses attenuated backscatter profiles from the CALIOP satellite lidar to estimate cloud base heights of lower-troposphere liquid clouds (cloud base height below approximately 3 km). Even when clouds are thick enough to attenuate the lidar beam (optical thickness τ≳5), the technique provides cloud base heights by treating the cloud base height of nearby thinner clouds as representative of the surrounding cloud field. Using ground-based ceilometer data, uncertainty estimates for the cloud base height product at retrieval resolution are derived as a function of various properties of the CALIOP lidar profiles. Evaluation of the predicted cloud base heights and their predicted uncertainty using a second statistically independent ceilometer dataset shows that cloud base heights and uncertainties are biased by less than 10 %. Geographic distributions of cloud base height and its uncertainty are presented. In some regions, the uncertainty is found to be substantially smaller than the 480 m uncertainty assumed in the A-Train surface downwelling longwave estimate, potentially permitting the most uncertain of the radiative fluxes in the climate system to be better constrained. The cloud base dataset is available at https://doi.org/10.1594/WDCC/CBASE.

1 Introduction

The base height z is an important geometric parameter of a cloud, controlling the cloud's longwave radiative emission, being required in the calculation of the cloud's subadiabaticity, and setting the level at which aerosol concentration and updraft speed determine the cloud's microphysical characteristics. However, due to the viewing geometry, it is also one of the most difficult cloud parameters to retrieve from satellites.

Multiple methods have been proposed for satellite determination of the cloud base height. Zhu et al. (2014) have used the Visible Infrared Imaging Radiometer Suite aboard the Suomi National Polar-orbiting Partnership satellite (VIIRS; Cao et al., 2014) to estimate cloud base temperature T_b from the lowest cloud top temperature within a cloud cluster; a reanalysis temperature profile can be used to convert T_b to z. Using an empirical relationship between geometric and optical thickness, Fitch et al. (2016) have obtained z from VIIRS. Cloud geometric thickness (and therefore z if the cloud top height is known) can be inferred from increased spectral absorption by O₂ within cloud due to multiple scattering (Kokhanovsky and Rozanov, 2005; Lelli and Vountas, 2018). Stereoscopic determination of the height of the most reflective layer (Naud et al., 2005, 2007) in Multiangle Imaging Spectroradiometer data (MISR, Diner et al., 1998) yields information on z, as the lowest layer heights within a cloud cluster may correspond to the base of a cloud seen from its side. An evaluation of MISR techniques is described in Böhm et al. (2018).

For analyses wishing to combine cloud base information with other cloud properties retrieved by A-Train satellites, these methods share the disadvantage that the required instruments are not part of the A-Train. Methods that are applicable to A-Train satellites are based on Moderate-Resolution Imaging Spectroradiometer (MODIS; Platnick et al., 2017) cloud properties retrieved near the cloud top and integrated along moist adiabats to determine the cloud thickness (Meerkoetter and Zinner, 2007; Goren et al., 2018) or on active remote sensing by CloudSat (2B-GEOPROF; Marchand et al., 2008) or a combination of CloudSat and CALIOP (2B-GEOPROF-LIDAR; Mace and Zhang, 2014). Each of these has drawbacks. The MODIS-derived cloud thickness assumes adiabatic cloud profiles and therefore cannot be used to constrain subadiabaticity; the use of ancillary temperature profile estimates may also be problematic in many cases. CloudSat misses the small droplets at the base of nonprecipitating clouds (Sassen and Wang, 2008), and retrievals are further degraded in the ground clutter region (Tanelli et al., 2008; Marchand et al., 2008). CALIOP detects the bases of only the thinnest clouds (τ<5; Mace and Zhang, 2014); frequently, it is desirable to know the base height of thick clouds as well.

In this paper, we revisit the CALIOP cloud base determination. We rely on one central assumption, namely that, because the lifting condensation level is approximately homogeneous within an air mass, the cloud bases retrieved by CALIOP for thin clouds are a good proxy for the cloud base heights of an entire cloud field, including the optically thicker clouds within the field. We have designed an algorithm that extrapolates the CALIOP cloud base measurements into locations where CALIOP attenuates before reaching cloud base. This algorithm is called Cloud Base Altitude Spatial Extrapolator (CBASE). In this paper we evaluate its performance by comparing CBASE z against z observed by ground-based ceilometers.

The cloud base of interest in this analysis is the base of the lowest cloud in each column. Even if CALIOP can also detect the base heights of other layers in multilayer situations, it is the base height of the lowest cloud that is of the greatest interest for many applications (e.g., surface radiation estimates).

Section 2 of this article describes the data sources used in determining and evaluating z. In Sect. 3 we describe the algorithm and evaluate its performance, including error statistics. The publicly available processed CBASE output is described in Sect. 4. Sections 5 and 6 document the availability of the code and dataset underlying this paper. We conclude in Sect. 1 with an outlook on the longstanding questions that the CBASE dataset can address.

Table 1 Data sources used in this analysis.

^* As a first step, ASOS station identifiers within a 100 km great-circle distance of a CALIOP footprint are identified; as a second step, the ICAO identifier of the ASOS station is then used to query the Weather Underground METAR database.

2 Data

Two classes of data are used in this work: cloud lidar data, from which we intend to derive a global z dataset, and ground-based observations used as reference measurements of z to train and evaluate the algorithm by which z is determined from the satellite data.

Table 1 lists the URLs for all datasets used in this paper.

2.1 CALIOP VFM

The input satellite data to our analysis are from the Cloud–Aerosol Lidar with Orthogonal Polarization (CALIOP; Winker et al., 2007) onboard the Cloud–Aerosol Lidar and Infrared Pathfinder Satellite Observation (CALIPSO) satellite that is part of the A-Train satellite constellation (Stephens et al., 2002) on a sun-synchronous low-Earth orbit with Equator crossings at approximately 13:30 local time. The cloud base product relies on the retrieved vertical feature mask (VFM; Vaughan et al., 2005). For each CALIOP lidar backscatter profile, the VFM identifies features such as clear air, cloud, aerosol, or planetary surface; this is termed the “feature type”. (When the lidar beam is completely attenuated, this is reported as a feature type.) In addition to the feature type, the VFM records the degree of confidence in the identification (“none” to “high”, termed the “feature type QA flag”), the thermodynamic phase of a layer identified as cloud as well as the degree of confidence therein (termed “ice water phase” and “ice water phase QA flag”), and the horizontal distance over which the algorithm had to average to identify a feature above noise and molecular atmospheric scattering (“horizontal averaging distance”).

In the present analysis, we use VFM version 4.10 (CALIPSO Science Team, 2016), the current standard release, for the years 2007 and 2008. The VFM files are obtained from ICARE (http://www.icare.univ-lille1.fr/, last access: 4 December 2018).

2.2 Airport ceilometers

For optimizing several parameters of the algorithm, for determining the expected cloud base uncertainty, and for evaluating the trained algorithm, reference measurements of z are required. The source of these “true” z values in this work is ground-based cloud observations at airports. Weather observations at airports are disseminated worldwide in aviation routine and special weather reports (METARs and SPECIs, collectively referred to as METARs henceforth; World Meteorological Organization, 2013). Apart from providing airport weather information for aviation, METAR data are used for assimilation into numerical weather prediction (NWP) models (e.g., Benjamin et al., 2016; Dee et al., 2011). In many locations, z reported in METARs is measured by a ceilometer over a period of time (tens of minutes) and then objectively grouped into cloud layers and their respective fractional coverages, using the temporal variation at a fixed point under an advected cloud field as a proxy for spatial variability in the cloud field (e.g., Heese et al., 2010). METAR data are widely distributed and archived; the data for the present analysis were downloaded from the Weather Underground archive (https://www.wunderground.com/history/airport/, last access: 4 December 2018).

In the US, z is mostly derived automatically by laser ceilometers that form part of the Automated Surface Observing Stations (ASOS, National Oceanic and Atmospheric Administration, Department of Defense, Federal Aviation Administration, and United States Navy, 1998) system; see, e.g., An et al. (2017) and Ikeda et al. (2017) for recent examples of ASOS application to deriving cloud climatologies or NWP model evaluation. In other parts of the world, the cloud bases may be estimated by human observers or may be omitted under certain conditions when the lowest cloud base is higher than 1524 m, complicating objective comparison to satellite z. To ensure that the ceilometer z values are of high and spatially uniform quality, we restrict ourselves to METARs from the contiguous continental US.

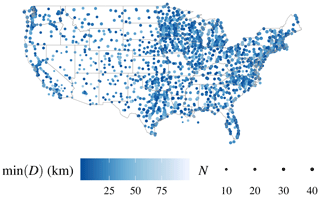
There are 1645 stations throughout the continental US that lie within 100 km of a CALIOP footprint. In normal operation, the time resolution of z reports is 1 h, but during rapidly changing conditions, more frequent updates may be provided; for comparison to satellite z, the ceilometer observation closest in time to the satellite overpass is used, provided that the time difference is less than 1 h. For training the algorithm, we use ceilometer observations from the year 2008. For unbiased evaluation of the algorithm performance, a statistically independent dataset is required; we use ceilometer observations from the same stations from the year 2007. Figure 1 shows the locations of these stations along with the number of satellite–ceilometer z coincidences and the closest co-location distance during the year 2007.

Figure 1 ASOS ceilometers used for CBASE z evaluation. The size of the marker indicates the number of satellite–ceilometer z coincidences during the year 2007. Color indicates the closest co-location distance achieved in 2007.

3 CBASE algorithm development and evaluation

The CBASE algorithm and evaluation proceed in four steps.

1. We determine the cloud base height from all CALIOP profiles in which the surface generates a return, indicating that the lidar is not completely attenuated by cloud. We refer to this as the column z_c in the sense that it is local to the CALIOP column.

2. Using ground-based ceilometer data, we determine the quality of cloud base height depending on a number of properties of the CALIOP profile. Assuming those properties suffice to determine the quality of the z_c estimate, we can then predict the quality of a cloud base as a function of those factors. The quality metric we use is the root-mean-square error (RMSE); the category RMSE determined from comparison to ceilometer z_c then serves as the (sample) estimate of the predicted (population) standard deviation of the measurement error $z_{\text{c}}-\widehat{z}$, i.e., the predicted z_c uncertainty. We denote this column uncertainty as σ_c. In the language of machine learning, we refer to this step as training the algorithm on the ceilometer data to predict z_c and σ_c.

3. Based on the predicted quality of each profile cloud base, we either reject the column cloud base or combine it with other cloud bases within a distance D_max of the point of interest to arrive at an estimate of z and σ at that point. We refer to z and σ as the CBASE cloud base height and cloud base height uncertainty.

4. Using a statistically independent validation dataset, we verify that the predicted z and σ are correct.

This section is divided into four subsections, one for each algorithm step enumerated above.

3.1 Determination of CALIOP column z

Profile z_c is determined from the CALIOP VFM for each profile with a surface return. The rationale is that a surface return indicates that the lidar did not attenuate within the cloud and that the lower limit of the layer identified as cloud therefore corresponds to the cloud base; Fig. 2 illustrates the idea. For these profiles, the location, z_c, cloud top height, feature type between the cloud base and the surface, cloud thermodynamic phase, and associated quality assurance flags from the VFM algorithm are recorded.

3.2 Determination of CALIOP column cloud base quality

We assess the quality of the CALIOP z_c using the RMSE with respect to the ceilometer-observed $\widehat{z}$. The RMSE is defined as

$$\begin{array}{}\text{(1)}& \text{RMSE}=\sqrt{{\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N{\left(z_{\text{c}}^i-\widehat{z}\right)}^{\mathrm{2}}}.\end{array}$$

The sum runs over all CALIOP profiles containing at least one cloud layer and a surface return that are within 100 km in horizontal distance of the ceilometer, occurring within 3600 s of a ceilometer observation, and having their lowest CALIOP cloud feature within 3 km of the surface. Ceilometer observations are only used if the observation closest in time to the CALIPSO overpass contains a cloud within 3 km of the surface. This height limit is imposed because a subset of the ceilometers has a range limit of 3810 m, and all ceilometers report ceilings above 3048 m with reduced granularity (152.4 m); the 3 km threshold is safely below these ceilometer limitations and mimics the International Satellite Cloud Climatology Project (ISCCP; Rossow and Schiffer, 1999) definition of low cloud (p>680 hPa).

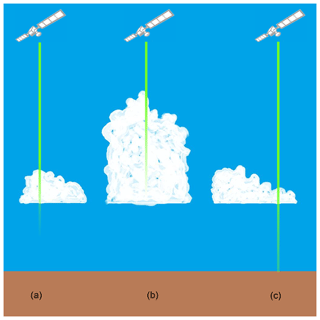
Figure 2 Schematic of CALIOP cloud base determination and evaluation strategy. In optically thick clouds (a, b), the lidar attenuates significantly within the cloud, rendering the cloud base information unreliable. However, z of thin clouds (c) can be used as a proxy for thick clouds in a cloud field with homogeneous z.

The following metrics, which are useful for a qualitative assessment of the quality of the satellite cloud base, are also calculated but play no quantitative role in the algorithm:

correlation coefficient

between the CALIOP cloud base and ground-based observation of the cloud base (we use the Pearson correlation coefficient, ideally unity);

linear regression slope and intercept

(ideally 1 and 0, respectively);

retrieval bias,

defined as

$$\begin{array}{}\text{(2)}& \text{bias}={\displaystyle \frac{\mathrm{1}}{N}}\sum _{i=\mathrm{1}}^N\left(z_{\text{c}}^i-\widehat{z}\right)\end{array}$$

(ideally 0).

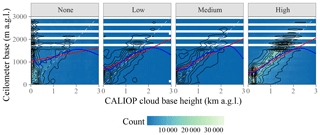
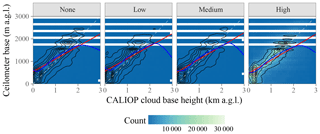
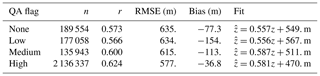
Figure 3 Scatter plots of CALIOP versus ceilometer cloud base height faceted by the CALIOP VFM QA flag; all CALIOP profiles meeting the temporal and spatial collocation requirements with a METAR enter into this plot. Color indicates the number of CALIOP profiles within each bin of ceilometer and CALIOP z; black lines are contours of the empirical joint probability density; the red line is a linear least-squares fit, with the 95 % confidence interval shaded in light red; the blue line is a generalized additive model regression (Wood, 2011), with the 95 % confidence interval shaded in light blue (due to the large dataset, the line width exceeds the confidence intervals in these plots); the dashed gray line is the one-to-one line. Statistics of the relationship between CALIOP and ceilometer base heights are provided in Table 2.

Table 2 Statistics of the relationship between ceilometer and CALIOP cloud base height faceted by the CALIOP VFM QA flag. Shown are the number of CALIOP profiles n, the product-moment correlation coefficient r between CALIOP and ceilometer z, the RMSE, bias, and linear least-squares fit parameters.

CALIOP's ability to detect cloud base depends on the properties of the cloud. Therefore, we expect that the z_c quality will vary among different cloud profiles. We expect that measuring the quality as a function of various properties of the CALIOP column will allow us to predict the quality of other columns with the same combination of properties. The properties that are easily accessible in a single column and have substantial effects on quality are

• horizontal distance D from the ceilometer,

• number of column cloud bases within horizontal distance D_max,

• CALIOP VFM feature quality assurance flag,

• geometric thickness of the lowest cloud layer,

• CALIOP thermodynamic phase determination of the lowest cloud,

• feature type, if any, detected between the lowest cloud and the surface, and

• horizontal averaging distance required for CALIOP cloud feature detection.

For illustrative purposes, Fig. 3 and Table 2 summarize the joint distribution of CALIOP and ceilometer z_c faceted by the CALIOP VFM feature quality assurance flag.

Figure 4 As in Fig. 3, but applying all requirements listed in Sect. 3.3.

Table 3 As in Table 2, but applying all requirements listed in Sect. 3.3.

Based on determining the retrieval quality as a function of one variable at a time (integrating over the sample distribution of the remaining variables), the following classes of CALIOP profiles are discarded:

• CALIOP VFM quality assurance worse than “high”,

• “invalid” or “no signal” layers between the surface and the lowest cloud layer (indicating that although the surface may generate a detectable return, the lidar is sufficiently attenuated that the cloud base, which scatters less strongly than the surface, is unreliable),

• minimum CALIOP cloud detection horizontal averaging distance within the lowest cloud layer greater than 1 km (indicating that, although average cloud properties are known at the averaging length scale, those properties may not be representative of the particular CALIOP footprint under consideration), or

• thermodynamic phase of the lowest layer determined to be other than liquid by the CALIOP VFM algorithm (the reason for this is that not enough such columns exist to determine the RMSE reliably in each of the categories defined below).

Figure 4 and Table 3 summarize the joint distribution of CALIOP profile z_c and ceilometer $\widehat{z}$ after these selection criteria for comparison with the unfiltered joint distributions in Fig. 3.

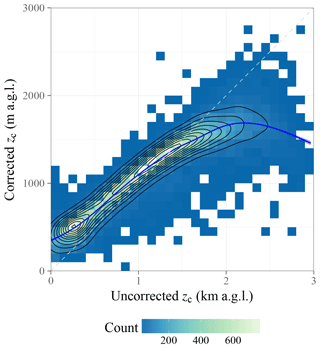
Figure 5 Density estimates of the projection of the SVM correction function. The training dataset (ceilometer overpasses in 2008) is used as the ensemble for performing the projection.

The remaining variables are discretized roughly into quintiles of their distribution within the VFM dataset with the following boundaries:

• horizontal distance D from the ceilometer, with boundaries 0, 40, 60, 75, 88, and 100 km (distance greater than 100 km is discarded);

• number of CALIOP columns n with a cloud layer and a surface return within 100 km in horizontal distance from the ceilometer, with boundaries at 0, 175, 250, 325, and 400 (multiplicity greater than 400 is accepted); and

• geometric thickness Δz of the lowest cloud layer, with boundaries at 0, 0.25, 0.45, 0.625, and 1 km (thickness greater than 1 km is accepted).

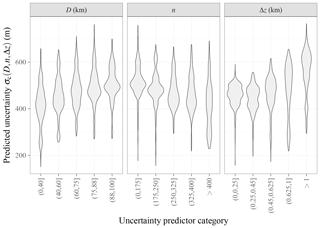
Figure 6 Density estimates of the projection of ${\mathit{\sigma }}_{\text{c}}(D,n,\mathrm{\Delta }z)$ onto each of the uncertainty predictor variables. The training dataset (ceilometer overpasses in 2008) is used as the ensemble for performing the projection.

We can now consider the joint distribution of CALIOP and ceilometer cloud bases for each combination of the above variables to derive the RMSE of each combination. Throughout this work, we use cloud base height above ground level (AGL); using height above mean sea level would introduce an intrinsic correlation between satellite and ceilometer cloud base height due to the varying terrain height, which would lead to an unrealistically positive assessment. To convert cloud base heights to AGL height, we subtract the surface elevation contained in the CALIOP VFM data files, which in turn comes from the CloudSat R05 surface digital elevation model.

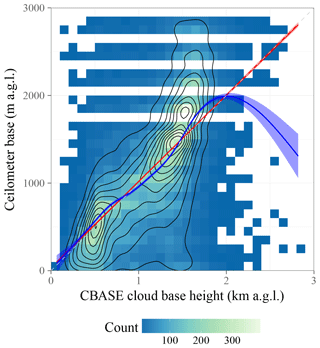
Figure 7 Scatter plot of CBASE versus ceilometer z for all A-Train overpasses over the contiguous US available for 2007; for description of the plot elements, see Fig. 3. The linear fit has a slope of 0.98 and an intercept of 33.96 m.

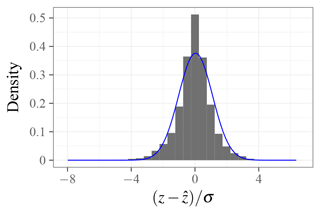
Figure 8 Distribution function of cloud base error divided by predicted uncertainty; for the ideal case of unbiased z and unbiased uncertainty, the distribution would be Gaussian with zero mean and unit standard deviation. The superimposed least-squares Gaussian fit (blue line) has a mean of 0.04 and standard deviation of 1.06.

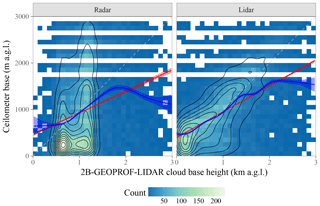
Figure 9 Scatter plot of 2B-GEOPROF-LIDAR versus ceilometer z faceted by the source of the cloud base (radar only or lidar only; due to their rare occurrence, combined radar–lidar base heights are not shown). For description of the plot elements, see Fig. 3. Statistics of the relationship between 2B-GEOPROF-LIDAR and ceilometer base heights are provided in Table 5.

When calculating aggregate statistics such as the RMSE, a further consideration comes into play. z_c above ground is positive-definite, which imposes a physical phase-space boundary. Due to this boundary, the satellite z_c estimate is intrinsically biased high (negative excursions due to symmetric random error may be removed by the phase-space boundary, but positive excursions are not), and the bias decreases with increasing satellite z_c estimate (when true z_c is high, it is less likely that measurement error would lead to a negative AGL z_c). Since this effect constitutes a bias rather than a random error, it cannot be eliminated by averaging over large sample sizes, but instead needs to be corrected for. Since the effect is nonlinear in z_c, a nonlinear correction method is required. Our choice of nonlinear bias correction is the support vector machine (SVM; Cortes and Vapnik, 1995). The SVM is a machine-learning algorithm formulated to learn classification (Cortes and Vapnik, 1995) or regression (Vapnik, 1995) tasks from a training dataset, discarding outliers and accommodating nonlinear functions (e.g., Smola and Scholkopf, 2004). We train an ϵ-regression SVM, implemented as an R package (Meyer et al., 2018) using the LIBSVM library (Chang and Lin, 2011), separately for each D, n, and Δz category, using the 2008 ceilometer overpass training dataset. The correction function is not trivial to represent because of its dependence on z_c, D, n, and Δz (which can be correlated). To reduce the dimensionality of this multivariate correction, we have used the training dataset (with its joint distribution of z_c, D, n, and Δz) to calculate an ensemble of correction factors that can be expected in a realistic sample of clouds, shown in Figure 5. The full multivariate correction function, implemented in R, is available from Mülmenstädt (2018).

Following bias correction, the sample RMSE is calculated for each combination of D, n, and Δz. The sample RMSE is taken as an estimate of the statistical uncertainty σ_c $(D,n,\mathrm{\Delta }z)$ on the CALIOP profile z_c. Note that D and Δz exist for each profile, whereas n is defined for the group of suitable profiles around the point of interest. Since the predicted uncertainty is multivariate, it is also nontrivial to visualize. We again use the training dataset as an ensemble on which to perform one-dimensional projections of σ_c $(D,n,\mathrm{\Delta }z)$ onto each of the predictor variables. These projected σ_c density estimates are shown in Fig. 6. The full multivariate σ_c prediction function, implemented in R, is available from Mülmenstädt (2018).

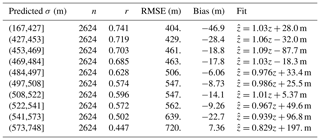
Table 4 CBASE cloud base statistics by decile of predicted uncertainty; see Table 2 for a description of the statistics provided.

3.3 Combination of column cloud bases

CALIOP z only exists sporadically, when CALIOP happens to hit a sufficiently thin cloud. To infer the z at a point of interest that does not necessarily coincide with the location of a thin-cloud CALIOP column, we proceed as follows. We first select all CALIOP column z_c measurements within a horizontal distance D_max=100 km of the point that satisfy the additional quality cuts described in Sect. 3.2.

For each remaining column z_c,i, we determine the predicted uncertainty σ_c,i based on the categories established in the previous section. We determine a combined z

$$\begin{array}{}\text{(3)}& z={\displaystyle \frac{\sum _i^n{w}_i{z_{\text{c}}}^i}{\sum _i^n{w}_i}}\end{array}$$

with weights

$$\begin{array}{}\text{(4)}& w_i={\displaystyle \frac{\mathrm{1}}{{\mathit{\sigma }}_{\text{c},i}^{\mathrm{2}}}}\end{array}$$

(optimal weights for uncorrelated least squares). The sum is calculated over the n z_c estimates within D_max that satisfy all criteria listed in the previous subsection. In practice, the individual measurements of cloud base are highly correlated with fairly similar σ_i. The cloud base estimate by Eq. (3) with weights given by Eq. (4) remains unbiased even in the presence of correlations. However, for the combined cloud base uncertainty, the uncorrelated weights would yield a biased estimate in the presence of correlations. The expression

$$\begin{array}{}\text{(5)}& {\mathit{\sigma }}^{\mathrm{2}}={\displaystyle \frac{\mathrm{1}}{n}}\sum _i^n{\mathit{\sigma }}_{\text{c},i}^{\mathrm{2}}\end{array}$$

yields acceptable results, as would be expected for highly correlated and fairly similar σ_c,i.

3.4 Evaluation of CBASE z and σ

Having trained the algorithm on data from the year 2008, we evaluate it using a statistically independent dataset from the year 2007. In the evaluation dataset, the true (i.e., ceilometer-measured) $\widehat{z}$ is known in addition to the estimated z and the estimated cloud base uncertainty σ, determined according to the procedure described in the previous section. Figure 7 shows the joint distribution of CBASE z and ceilometer-observed $\widehat{z}$.

For satellite-derived measurements of z that are unbiased with respect to the ceilometer-observed $\widehat{z}$ and have correctly estimated uncertainties σ, the probability density function of the quantity $(z-\widehat{z})/\mathit{\sigma }$ has zero mean and unit standard deviation. In our evaluation dataset, we find a mean of 0.04 and a standard deviation of 1.06, shown in Fig. 8; this corresponds to a z bias of 4 % and uncertainty bias of 6 %, both relative to the predicted uncertainty. Thus, we find that both the cloud base estimate and the uncertainty estimate are unbiased at better than the 10 % level.

As a further test of the reliability of the expected uncertainty, we divide the validation dataset into deciles of the expected uncertainty. Table 4 shows that the actual RMSE within each decile is within 10 % of the expected uncertainty (with the exception of the highest-uncertainty decile) and that linear regressions within each decile are close to the one-to-one line.

To check that the algorithm satisfies its design constraints (i.e., to ensure that we made no methodological error when implementing the algorithm), we have also verified that linear regression between z and $\widehat{z}$ has zero intercept and unit slope and that the quantity $(z-\widehat{z})/\mathit{\sigma }$ has zero mean and unit standard deviation when this validation is performed on the training dataset.

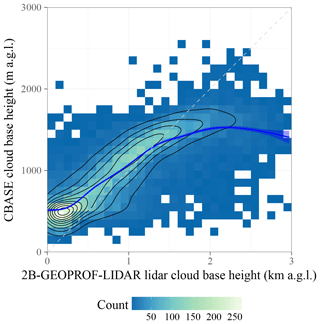
Figure 10 Scatter plot of 2B-GEOPROF-LIDAR lidar-only versus CBASE z. For description of the plot elements, see Fig. 3; because both cloud base measures have comparable uncertainty, linear regression is a misleading diagnostic (Pitkanen et al., 2016) and has not been included. The mean difference between 2B-GEOPROF-LIDAR and CBASE is 0.05 km, the root-mean-square difference is 0.41 km, and the correlation coefficient is 0.79.

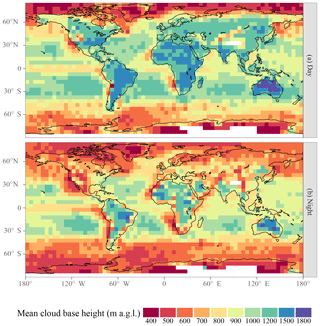
Figure 11 Geographic distribution of mean z above ground level. Statistics are calculated within each ${\mathrm{5}}^{\circ }\times {\mathrm{5}}^{\circ }$ latitude–longitude box and separately for CALIOP daytime (a) and nighttime (b) overpasses.

It is possible that z estimates outside North America could have greater biases or greater uncertainty than this evaluation leads us to believe. This would be the case if continental clouds over North America are not representative of clouds elsewhere in a way that is not accounted for by the cloud properties considered by the uncertainty estimate. Since the validation sample spans an entire year on a continental scale, we expect that most cloud morphologies are included. However, cloud types that occur predominantly over ocean, namely marine stratocumulus with horizontally extensive but vertically thin liquid-phase anvils, present a particular challenge to the method. Due to the typical z uncertainty of several hundred meters, the method is unlikely to be applied to stratocumulus cloud; nevertheless, a marine-cloud validation dataset would be desirable. For the present work, no suitable marine-cloud evaluation dataset was available; ship-based z observations were either based on human observers with coarse vertical resolution and a precision that is difficult to characterize or available only over a limited duration at limited locations, resulting in a severely statistics-limited set of coincidences with the CALIOP track.

3.5 Comparative evaluation of CBASE and 2B-GEOPROF-LIDAR

Comparison with 2B-GEOPROF-LIDAR cloud bases (version P2_R04_E02, based on the 2B-GEOPROF and CALIOP VFM products) is shown in Fig. 9. 2B-GEOPROF-LIDAR distinguishes among radar-only, lidar-only, and radar–lidar combined cloud bases; the last category is rare for warm clouds and is not shown. For radar-only clouds, the mean error is large because the radar z predominantly clusters around the top of the ground clutter region with little dependence on the actual z.

Lidar-only 2B-GEOPROF-LIDAR cloud base performs comparably to the CBASE cloud base on average; this is to be expected, as the underlying physical measurement (the CALIOP attenuated backscatter) is the same for all three products considered (2B-GEOPROF-LIDAR, CALIOP VFM, and CBASE). Figure 10 shows the relationship between CBASE z and the 2B-GEOPROF-LIDAR cloud base closest to the ceilometer for each overpass. The CBASE z for low clouds tends to be higher than the 2B-GEOPROF-LIDAR estimate because the CBASE algorithm has been designed to agree with ceilometer heights, which also tend to be higher than the 2B-GEOPROF-LIDAR estimate (see Fig. 9). Otherwise, the relationship is fairly close (linear correlation coefficient of 0.79), again as expected due to the similarity in the underlying measurement.

Figure 12 Distribution of predicted z uncertainty σ.

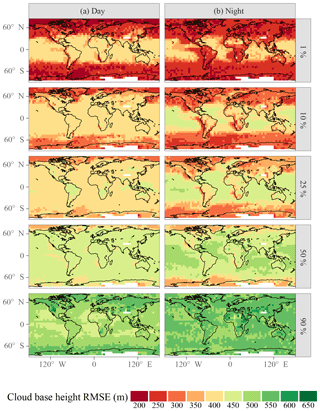
Figure 13 Cloud base uncertainty quantiles. Statistics are calculated within each ${\mathrm{5}}^{\circ }\times {\mathrm{5}}^{\circ }$ latitude–longitude box. Panels (a) and (b) show statistics of daytime and nighttime retrievals, respectively; daytime and nighttime are defined by the CALIOP VFM product.

Unlike 2B-GEOPROF-LIDAR and the CALIOP VFM, CBASE provides a validated point-by-point uncertainty estimate, which allows an analysis to select only low-uncertainty cases or to statistically weight z according to uncertainty, as appropriate for the application.

Table 5 Statistics of the relationship between ceilometer and 2B-GEOPROF-LIDAR z; see Table 2 for a description of the statistics provided.

Figure 14 Uncertainty on the surface downwelling longwave radiation $F_{\text{surf}}^{\downarrow }$ under two assumptions of z uncertainty: (a) constant 400 m uncertainty globally and (b) uncertainty achievable by selecting a high-quality subset of CBASE z.

4 Results

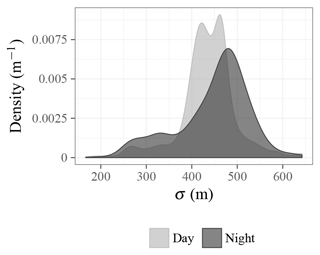
Geographic distributions of the mean z are shown for daytime and nighttime CALIPSO overpasses in Fig. 11. Over most of the globe, especially over land, daytime z is higher than nighttime z, consistent with the diurnal deepening of the planetary boundary layer. Figures 12 and 13 show the distribution of z uncertainties. A larger fraction of nighttime cloud bases falls into the lowest uncertainty range (200 to 350 m), while the the nighttime uncertainty distribution peaks slightly higher than the daytime uncertainty distribution and features a substantial tail above 500 m that is not present in the daytime distribution. CALIOP benefits from a higher signal-to-noise ratio during nighttime, which may lead to lower σ, but this effect would be convoluted with potential differences between daytime and nighttime clouds that can lead to different z uncertainties. Training a potential future update of the algorithm on daytime and nighttime profiles separately may reduce σ.

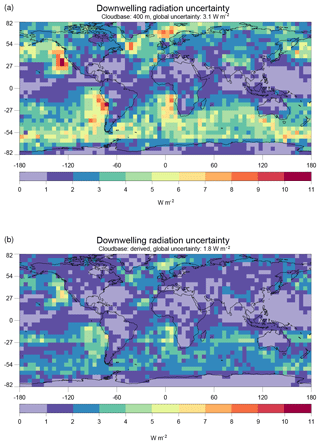
As an example application, we consider the surface downwelling longwave radiation $F_{\text{surf}}^{\downarrow }$, which is strongly affected by cloud base temperature. Henderson et al. (2013) derive a global $F_{\text{surf}}^{\downarrow }$ sensitivity to z of 1.5 W m⁻² for a z perturbation of one CloudSat height bin (240 m); as Table 5 and Fig. 9 show, the CloudSat σ specifically for the low clouds at the focus of the present work is likely greater than 240 m, which corroborates the 480 m uncertainty estimate of Kato et al. (2011). To arrive at a conservative estimate of the improvement in $F_{\text{surf}}^{\downarrow }$ uncertainty that might be possible by utilizing the CBASE predicted σ, we compare two $F_{\text{surf}}^{\downarrow }$ uncertainty distributions: one based on a globally constant 400 m σ (Fig. 14a) and one with the CBASE σ achievable by selecting the highest-quality percentile of the CBASE dataset (Fig. 14b). This selection provides a σ of approximately 250 m in the extratropics as well as the nighttime tropical continents and stratocumulus regions and approximately 400 m throughout the tropics during daytime, according to Fig. 13. Globally, the $F_{\text{surf}}^{\downarrow }$ uncertainty is reduced from 3.1 to 1.8 W m⁻², assuming that the z uncertainty contribution to the $F_{\text{surf}}^{\downarrow }$ uncertainty is dominated by low clouds. Improvements are especially large in the marine stratocumulus regions and the extratropical oceans, where extensive low cloud often overlies cool air with relatively low longwave emission by water vapor. The selection reduces the available statistics by a factor of 100, but analyses based on A-Train data are usually not statistics limited.

5 Code availability

The source code used to produce the dataset and evaluation plots is available from Mülmenstädt (2018).

6 Data availability

The CBASE z and σ dataset (Mülmenstädt et al., 2018) spanning the years 2007 and 2008 is freely available at Deutsches Klimarechenzentrum (DKRZ) under the DOI https://doi.org/10.1594/WDCC/CBASE. The dataset is provided in two spatial resolutions corresponding to different window sizes within which CALIOP profiles are combined: D_max=40 km and D_max=100 km. CBASE provides two files for each CALIOP VFM input file: one using a 40 km window to detect the cloud field base height and one using a 100 km window. (The input CALIOP VFM dataset is organized by the daytime (D) and nighttime (N) half of each orbit.) The file name pattern is CBASE - {40|100}. < date > T < time > {D|N}.nc (identical to the input CALIOP VFM file name with the exception of the product name and file-type extension). Files are organized into subdirectories by half orbit start date. In case no cloud base heights are detected within a half-orbit, no output file is produced. Otherwise, each CALIOP VFM input file results in a 40 km resolution and a 100 km resolution CBASE file. The measurement quality is reported as a quantitative uncertainty estimate for each cloud field.

7 Conclusions

We have presented the CBASE algorithm, which derives the cloud base height z from CALIOP lidar profiles. This algorithm produces z not only for thin clouds but also for clouds thick enough to attenuate the lidar (optical thickness τ≳5), based on the assumed mesoscale homogeneity of cloud base height within an air mass. In addition to the z estimate, the CBASE algorithm supplies an expected uncertainty σ on z. The CBASE dataset is available for the years 2007 and 2008 at https://doi.org/10.1594/WDCC/CBASE.

CBASE z and σ have been evaluated using ground-based airport ceilometers over the contiguous US using a data sample unbiased by the training of the algorithm. The evaluation showed that z and σ are unbiased at the level better than 10 %: the bias on z is 4 %, and the bias on the uncertainty is 6 %, both relative to the expected uncertainty.

The performance of CBASE z is similar to that of 2B-GEOPROF-LIDAR lidar-only z when validated against the same collocated ceilometer measurements, which is based on the same underlying physical measurement. However, the validated z uncertainty provided by CBASE allows for selection of only accurate cloud base heights or for statistical weighting of z according to expected uncertainty. This, in turn, makes the CBASE z useful for pressing problems in climate research that require accurate knowledge of cloud geometry, such as surface downwelling longwave radiation or cloud subadiabaticity, which will be presented in future work.