PRODEM: an annual series of summer DEMs (2019 through 2022) of the marginal areas of the Greenland Ice Sheet

Surface topography across the marginal zone of the Greenland Ice Sheet is constantly evolving in response to changing weather, season, climate, and ice dynamics. However, current digital elevation models (DEMs) for the ice sheet are usually based on data from a multi-year period, thus obscuring these changes over time. Here we present four 500 m resolution summer DEMs (PRODEMs) of the Greenland Ice Sheet marginal zone for 2019 through 2022. The PRODEMs cover the marginal zone from the ice edge to 50 km inland, hence capturing all Greenland outlet glaciers. Each PRODEM is based on data fusion of CryoSat-2 radar altimetry and ICESat-2 laser altimetry using regionally varying kriging of elevation anomalies relative to ArcticDEM. The PRODEMs are validated using leave-one-out cross-validation, and PRODEM19 is further validated against an external data set, showcasing their ability to correctly represent surface elevations within the associated spatially varying prediction uncertainties. We observe a general lowering of surface elevations during the 4-year PRODEM period, but the spatial pattern of change is highly complex and with annual changes superimposed. The PRODEMs enable detailed studies of the marginal ice sheet elevation changes. With their high spatio-temporal resolution, the PRODEMs will be of value to a wide range of researchers and users studying ice sheet dynamics and monitoring how the ice sheet responds to changing environmental conditions. PRODEMs from summer 2019 through 2022 are available at https://doi.org/10.22008/FK2/52WWHG (Winstrup, 2024), and we plan to annually update the product henceforth.

1 Introduction

During the past few decades, the Greenland Ice Sheet has lost mass at an increasing rate (Mankoff et al., 2021; Otosaka et al., 2023; Simonsen et al., 2021; The IMBIE Team, 2020), contributing to global sea level rise (Moon et al., 2018; WCRP Global Sea Level Budget Group, 2018). The largest changes take place near the margin of the ice sheet. Most of the ice sheet margin experiences a large and progressive thinning, but the response is highly heterogeneous, due to the impacts and feedback from temperature, precipitation, and ice flow (Krabill et al., 2004; Sørensen et al., 2018). Coupled ice sheet–climate models suggest that future ice loss from the Greenland Ice Sheet will primarily be driven by changes in surface mass balance, particularly increased ablation at the ice sheet margin due to atmospheric warming (Quiquet and Dumas, 2021).

The ice sheet marginal zone, here defined as a 50 km periphery of the ice sheet, is characterized by a complex interplay of processes. Several feedback loops involve topography and elevation, including, but not limited to, elevation–temperature feedback, local and regional weather, hydrology, and ice dynamics. The elevation–temperature feedback loop means that as the ice sheet thins, the lower surface will be exposed to higher temperatures (van As et al., 2017), leading to increased surface melt and further thinning (Aschwanden et al., 2019; Delhasse et al., 2024). The ice sheet geometry also affects local and regional weather patterns (Ettema et al., 2009). As orographic precipitation is the main driver of Greenland precipitation in coastal areas (Lenaerts et al., 2019), changes in topography may greatly impact precipitation patterns, thereby influencing the surface mass balance. Further, changing surface slopes and ice thicknesses will change both supra- and subglacial hydrological networks, with subsequent impacts on ice flow (Andrews et al., 2018; Maier et al., 2023). Lastly, changing surface slopes will alter the ice-flow driving stress regime, with increased slopes due to greater marginal thinning rates hastening the ice loss (Wang et al., 2012).

Comprehensive monitoring of surface elevation for the Greenland Ice Sheet marginal zone is essential for enhancing our understanding of these and other dynamic processes. Developing accurate digital elevation models (DEMs) for the Greenland Ice Sheet, especially its marginal zone, will advance our understanding of ice sheet dynamics, the response of the ice sheet to ongoing environmental changes, and the consequent impact on global sea levels.

Two methods commonly used to produce large-scale DEMs for the Greenland Ice Sheet are satellite altimetry and photogrammetry of satellite imagery stereo pairs, possibly supplemented with airborne data from the margin. Satellite altimetry is based on either radar or laser, with laser altimetry providing a more direct surface measurement in higher along-track resolution but available only for a limited period. Due to sensor characteristics, DEMs from stereographic imagery have higher spatial resolution than those based on satellite altimetry, which is especially important in areas with high topographic variability, such as near the ice sheet periphery. However, to achieve large-scale coverage, DEMs from stereo-photogrammetry, such as ArcticDEM (Porter et al., 2023), currently rely on imagery from an extended period, leading to a relatively coarse temporal resolution. While the individual ArcticDEM strips have a specific time stamp, the ArcticDEM mosaic is, for example, based on data from a 15-year period, during which the ice sheet topography may have substantially changed. Of the multiple DEMs created for the Greenland Ice Sheet (see e.g. Bamber et al., 2001a; DiMarzio et al., 2007; Ekholm, 1996), only a few (Fan et al., 2022; Helm et al., 2014) have been temporally limited to include data from just a single year – an important factor in reducing uncertainty due to temporal changes.

This paper describes the derivation and validation of PRODEMs, an annual series (2019–2022) of summer DEMs for the ice sheet marginal zone. PRODEM is the first annual series of DEMs across this rapidly changing region, directly describing the evolving summer ice topography. The PRODEMs are created by fusing CryoSat-2 (radar) and ICESat-2 (laser) altimetry measurements acquired during the summer months, after referencing them to ArcticDEM elevations. The applied approach exploits the high spatial resolution of ArcticDEM, while enhancing these data with a temporal resolution based on satellite altimetry. Coverage of the PRODEMs in terms of area and season is restricted to areas minimally covered by snow and firn, over which the two satellite altimeters are expected to measure the same surface, and the PRODEMs hence represent the ice surface topography.

With individual high-resolution DEMs available for each summer, the PRODEM series allows detailed analyses of the annual changes in ice sheet geometry. The PRODEMs will be valuable for marginal mass balance assessments, as they provide crucial information on the inter-annual variability in surface elevation across these pivotal areas for understanding the complex interplay between the ice sheet, oceanic processes, and climate dynamics. Further, one specific use case of the PRODEM series is to improve mass balance assessments for the entire ice sheet based on the mass budget method (van den Broeke et al., 2009; Mankoff et al., 2021; Mouginot et al., 2019), in which the solid ice discharge is calculated by summing the contribution from all individual outlet glaciers based on measured ice velocity and ice thickness (Mankoff et al., 2020). The annually changing PRODEM surface elevations will support the ongoing assessment of solid ice discharge, as carried out, for example, within the Programme for Monitoring of the Greenland Ice Sheet (PROMICE) project (Ahlstrøm and the PROMICE project team, 2008).

2 Input data

To construct the PRODEMs, we combine summer elevation data from June through September from two satellite altimetry missions: ESA's radar mission CryoSat-2 (CS2) and NASA's laser mission ICESat-2 (IS2). Due to the different nature of the two satellite sensors, their altimetry observations have distinct properties, including differences in resolution and topographic sampling, as described below. We filter the satellite altimetry to include only measurements over ice-covered areas. The observed elevations are subsequently transformed into elevation anomalies relative to the ArcticDEM v4.1 gridded mosaic (Porter et al., 2023). All observations are referenced to the WGS84 datum, with elevations provided as heights (in metres) above the WGS84 ellipsoid.

2.1 CryoSat-2

The SAR Interferometric Radar Altimeter (SIRAL) on board CS2 has monitored the elevation changes of the Greenland Ice Sheet since July 2010 (Parrinello et al., 2018). SIRAL operates in two distinct modes over the ice sheet: the conventional low-resolution mode (LRM) and the advanced SAR interferometry (SARIn) mode. In LRM, the radar footprint is too large for reliable data collection in areas with highly varying topography as prevalent along the ice sheet margins. For these challenging regions, the SARIn mode is applied. The initial radar return signal (determined by “retracking” the radar waveforms) will arrive from the point of closest approach (POCA), and a radar altimeter will therefore tend to measure local topographic highs, causing a bias in measured mean elevations (Bamber, 1994; Hurkmans et al., 2012; Levinsen et al., 2016). In SARIn mode, the difference in signal phase received by SIRAL's two antennas is employed to constrain the across-track angle of the first radar returns, allowing the off-nadir origin of the echo (i.e. POCA) to be located (Wingham et al., 2006). Geolocation of the POCA is, however, associated with some uncertainty due to phase ambiguities, which may give rise to elevation outliers. The SARIn approach partially alleviates the locational ambiguity and slope-induced errors of conventional radar altimetry (Schröder et al., 2019), resulting in improved data accuracy and coverage across rough terrain. In SARIn mode, SIRAL has a footprint of ∼ 400 m along track and 1.65 km across track, corresponding to a total footprint area of 0.5 km² (ESA, 2023a).

The radar return signal depends on the surface properties. In areas covered by snow and firn, the radar signal may partially penetrate the surface. The return signal will therefore be a mixture of surface and volume scattering, leading to elevation biases dependent on subsurface properties and the applied retracker (Michel et al., 2014). In the bare ice zone, however, radar altimeters measure the ice surface without any elevation bias (Dall et al., 2001; Davis and Moore, 1993; Otosaka et al., 2020).

Here we primarily use CS2 SARIn altimetry for generating the PRODEMs. For a small part of the PRODEM area in southwest Greenland, CS2 is operated in LRM instead of SARIn mode, and in this small area, we include LRM CS2 altimetry. We use CS2 Ice Level 2 Baseline E data (ESA, 2023b) and remove data flagged as having issues with accurate elevation retrieval and/or cross-track angle error and hence geolocation error. Additionally, observations without relocation from nadir or with relocation distances exceeding 15 km are considered unrealistic, and these observations are also removed. On average, 23 %–24 % of the original data set is discarded, mostly due to cross-track angle errors.

2.2 ICESat-2

With the launch of IS2 in September 2018, extremely high resolution laser altimetry data for the Greenland Ice Sheet have become available. The ATLAS instrument on board IS2 is a single-photon-counting lidar (Markus et al., 2017). Laser-based altimeters have several advantages over radar altimeters, including a smaller footprint and negligible surface penetration. One drawback is, however, that data acquisition may be compromised by clouds and blowing snow.

IS2 is placed in a repeat-track orbit, measuring the same ground segments with a repeat period of 91 d. Each IS2 track consists of six beams separated into three pairs, with approximately 3 km between pairs and 90 m between adjacent beams within a pair (Markus et al., 2017). Each pair consists of one strong and one weak beam, and given the short distance between them, the measured elevations along the two beams are strongly correlated. Dense sampling in certain areas may lead to overfitting of local surface variations, thereby introducing biases or inaccuracies in the interpolated elevation fields. To avoid excessive oversampling along the beams, the PRODEMs are constructed using data only from the three strong beams.

We use the IS2 Land Ice Height data set ATL06 V6 (Smith et al., 2023), a down-sampled product where individual photon heights are averaged within 20 m segments along each beam (Smith et al., 2019). Observations flagged as bad data are removed (3 %–7 % depending on year). For consistency with the resolution of the CS2 observations, we further down-sample the ATL06 data by computing median values over 250 m along-track segments of each beam. Segments containing fewer than five elevation values (i.e. less than one-third) are discarded from the analysis. IS2 observations constitute 71 %–76 % of the total ice elevation measurements used for generating the PRODEMs.

2.3 ArcticDEM

All altimetry measurements are transformed to elevation anomalies relative to a reference DEM, for which we employ the 500 m resolution ArcticDEM v4.1 gridded mosaic (Porter et al., 2023).

Leveraging thousands of overlapping sub-metre resolution optical image pairs from the GeoEye and WorldView satellites, the accuracy and details offered by ArcticDEM (developed by the Polar Geospatial Center, University of Minnesota) have greatly improved our ability to study fine-scale topographic features across the Greenland Ice Sheet. ArcticDEM provides “strip” DEMs covering a narrow strip of area at a specific time (Noh and Howat, 2015), as well as a mosaic providing a seamless high-resolution (2 m) elevation model covering the entire Arctic. The newest version (v4.1) of the ArcticDEM mosaic (Porter et al., 2023) is based on an extended data set of stereo pairs acquired from 2007 through 2022 and constructed by taking the median elevation value at each pixel (after removal of outliers) from the collection of strip DEMs. For improved accuracy, stereo-photogrammetry requires registration to independent elevation data. The ArcticDEM v4.1 mosaic is constructed in tiles of 100×100 km, with each tile registered to the GrIMP DEM v2 (which itself is registered to IS2 elevations from the summers of 2019 and 2020) (Howat et al., 2022). The tiles are subsequently blended at the edges to match neighbouring tiles. However, edge-matching by blending and feathering of strips and tiles may introduce artefacts in the final mosaic. Furthermore, areas of low radiometric contrast, cloud cover, or shadows may introduce errors or data voids. Other error sources include slight misregistration of the stereo-pairs, which may lead to large elevation errors in areas with high topographic variability when combining individual strips of stereo imagery into a mosaic (Polar Geospatial Center, 2023).

We also employ ArcticDEM to estimate the varying surface roughness, which is used to compute the spatial component of the observation uncertainties (Sect. 4.1). A map of the 100 m scale surface roughness is obtained from the 100 m resolution ArcticDEM mosaic, computed as the largest elevation difference between the central pixel and its surrounding cells (Wilson et al., 2007). We note that with this definition a flat, sloping surface will have a roughness value depending on the slope.

3 PRODEM: coverage and resolution

3.1 Spatial and temporal coverage

The PRODEMs are summer DEMs for the marginal areas of the Greenland Ice Sheet, including peripheral glaciers connected to the ice sheet based on the BedMachine v5 ice cover mask (Morlighem et al., 2017, 2022). Each PRODEM in the series is independent. They are built entirely from summer data (1 June to 30 September), and the DEM coverage is limited to the outermost 50 km wide band of the ice sheet margin. To avoid edge effects in the DEMs, altimetry is incorporated from an extended area that includes a 10 km inland buffer zone. The PRODEM area covers most (∼ 90 %) of the summer bare ice zone (Fausto and the PROMICE team, 2018). The area and period are selected to ensure that the altimetry data primarily provide snow-free ice surface elevations, thereby largely eliminating the effect of different snow penetration depths of the radar versus the laser signal.

With the collected data from CS2 and IS2 combined, the data coverage is sufficient to derive high-resolution annual maps of ice sheet topography in the marginal areas of the Greenland Ice Sheet. Using 500 m grid resolution, the interpolation distances from the grid cell centres to the nearest data point show a distribution with a mode in the 120–230 m range and a median of 452 m (values for 2019 data; see histogram in Fig. 1a). Due to the denser satellite orbits towards the north, the interpolation distances tend to be smaller there. Within any region, the data coverage is irregularly spaced, and in a minority of cases, the accuracy of the interpolated elevations is significantly limited by data availability. This is especially an issue for the southernmost drainage basin (basin 5). Across all PRODEM grid cells, the closest point is more than 1 km away ∼ 15 % of the time but further away than 2 km only ∼ 3 % of the time. Most cells (∼ 85 %) have a sample point less than 1 km away (Fig. 1a).

Figure 1b–d show the 2019 data coverage in the regions around the three largest outlet glaciers from the Greenland Ice Sheet: Sermeq Kujalleq (Jakobshavn Isbræ), Kangerlussuaq Gletsjer, and Helheim Gletsjer. The observations are distributed differently in other years. Areas of lower data density will be reflected as regions of increased uncertainty in the derived PRODEM elevations for the given year, which are noticeable from the accompanying map of elevation field uncertainty provided with each PRODEM.

Figure 1 (a) Histogram showing the distribution of distances for each grid cell centre to the closest observation (data from 2019). Distributions are shown for each main drainage basin (blue colours for drainage basins in north and east Greenland; green colours for basins in south and west Greenland; colour saturation is relative to basin latitude) and for the entire PRODEM area (black). (b–d) CS2 and IS2 data coverage for June through September 2019 over subsectors covering the area around the three largest outlet glaciers from the Greenland Ice Sheet: Sermeq Kujalleq (b), Kangerlussuaq Gletsjer (c), and Helheim Gletsjer (d). IS2 data can be recognized as data acquired along straight lines, while CS2 data are geolocated according to the POCA. For the derivation of the PRODEMs, the ice sheet marginal zone was first divided up into subsectors using the drainage basin definitions from Zwally et al. (2012), which are indicated with numbers on the overview map of the Greenland Ice Sheet. Official glacier names from Bjørk et al. (2015).

3.2 Spatial resolution

The PRODEMs are constructed by evaluating the interpolated elevation anomaly field at the grid cell centres (an approach called “point kriging” (Hengl, 2009)). For this approach to accurately represent the mean field value within a grid cell, the grid resolution must align with the scale of variability of the observations. After downsampling of the IS2 data, both CS2 and IS2 data sets are representative of an area of a few hundred metres, and an appropriate resolution for the anomaly field of the interpolated PRODEMs is therefore on the order of 500 m.

4 Estimating uncertainties and bias of the satellite altimetry data

4.1 Observation uncertainties

During the DEM construction based on the CS2 and IS2 satellite altimetry, we include an estimate of uncertainty for each individual observation, which is used to weigh the contribution of each observation to the final interpolated DEM. If uncertainties are overestimated, the resulting field will be too smooth, thus discarding much of the information in the observations. Conversely, if uncertainties are underestimated, the interpolation may overfit the observations while inducing noise in the interpolated field. Nevertheless, the observation uncertainties have been largely disregarded during the construction of existing altimeter-derived ice sheet DEMs.

The observation uncertainty should be understood as a measure for how accurately an observation is representative of the mean elevation field (spatially and temporally) at a given location. The degree to which an observation represents the mean elevation field may be divided into four factors, which together constitute the total uncertainty: the instrument measurement uncertainty (σ_meas; including the uncertainty in, for example, retracker algorithms), the elevation uncertainty caused by potential errors in the geolocation of the observation (σ_geo; affected observations are assumed to be identified as outliers and removed through filtering; see Sect. 5.2), along with the spatial (σ_spatial) and temporal (σ_temp) representability of an observation. Appropriate values for the latter two depend on the elevation field to be interpolated. σ_spatial is a measure of how well an observation represents the average elevation field within a DEM grid cell, which depends on the spatial variability (roughness and slope) of the local elevation field. Further, the observations are collected within a 4-month window, during which the ice sheet surface topography evolves due to surface mass balance and/or dynamic changes. σ_temp is a measure for how well a given observation represents the mid-summer elevation at its location, which depends on the temporal difference between mid-summer and the observation acquisition date.

In the following, we develop separate uncertainty models for the spatially varying uncertainty of the CS2 and IS2 sensors (σ_spatial, convolved with the contribution from σ_meas) and a common model for the temporal uncertainty component (σ_temp). The total observation uncertainty is calculated by combining the two uncertainty components in quadrature as if they are independent and uncorrelated, although this assumption is not entirely true (as one example, the ice sheet periphery tends to be subject to both high roughness and large seasonal elevation trends (Slater et al., 2021b), leading to high spatial as well as temporal uncertainty).

4.1.1 Measurement and spatial uncertainty of the CS2 elevations

To estimate the CS2 spatial uncertainty, we analyse the measured elevation differences at temporally close intersecting CS2 satellite tracks within our study area, in an approach inspired by the cross-over methods used for deriving local longer-term elevation change rates (Khvorostovsky et al., 2003; Sørensen et al., 2018). We compare the closest pairs of observations located within 50 m of each other and acquired within 15 d. Prior to comparison, the elevations are adjusted relative to ArcticDEM to account for local slope. The observed elevation differences are primarily a result of small-scale topographic variability, although short-term elevation changes due to, for example, intermittent snowfall may also play a minor role. For areas with little topographic relief, the measurement uncertainty will dominate.

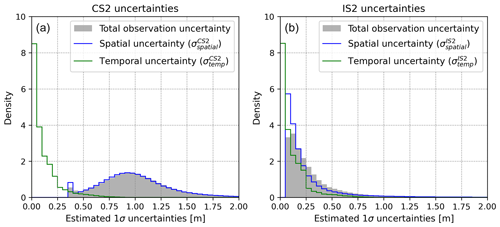
A total of 5873 close-in-time intersecting CS2 tracks exist within our study area during summers 2019 through 2022. The resulting distribution of observed elevation differences near the track intersections is sharply peaked around 0 m (Fig. 2a; grey histogram), with a median absolute deviation (MAD) of 0.86 m. While not strictly adhering to a Gaussian distribution (Fig. 2a,c), an approximate standard deviation describing the spread of the distribution can be obtained using normalized MAD (nMAD): $\mathrm{nMAD}=\mathrm{1.4826}\cdot \mathrm{MAD}$. This approach has the advantage of being more robust to outliers than a direct calculation of the standard deviation. As the distribution of elevation differences includes the error sources from both elevation measurements, an approximate measure of the 1σ uncertainty of the CS2 observations can be derived as

$$\begin{array}{}\text{(1)}& {\mathit{\sigma }}_{\mathrm{spatial}}^{\mathrm{CS}\mathrm{2}}\approx {\displaystyle \frac{\mathrm{nMAD}}{\sqrt{\mathrm{2}}}}={\displaystyle \frac{\mathrm{1.4826}}{\sqrt{\mathrm{2}}}}\cdot \mathrm{MAD}.\end{array}$$

The mean uncertainty of all CS2 observations due to spatial variability of the terrain is found to be 0.90 m. However, as this uncertainty is spatially variable, such a single uncertainty value is inappropriate: in areas of sloping and/or rough terrain, the spatial representativeness of any given observation will be smaller.

We investigate the variability in CS2 spatial uncertainty by examining the relationship between local 100 m scale surface roughness (obtained from ArcticDEM) and the dispersion of measured elevation differences near intersecting satellite tracks. Binning the satellite crossings according to the local roughness, statistics for the distributions of measured elevation differences are computed for different roughness values. The observations are divided into 20 roughness bins, each containing a sufficiently large number (∼ 280) of observations to obtain good estimates for MAD, with extreme roughness values (above the 95th percentile) excluded due to poorly constrained statistics. A linear relationship exists between the logarithm to the local 100 m scale roughness and ${\mathit{\sigma }}_{\mathrm{spatial}}^{\mathrm{CS}\mathrm{2}}$ (Fig. 2b), while plateauing at a value of 0.39 m for low roughness values (log(roughness) < 0, i.e. roughness < 1 m). At these locations with little slope and surface irregularity, the total observation uncertainty is dominated by the measurement uncertainty, and we thus evaluate ${\mathit{\sigma }}_{\mathrm{meas}}^{\mathrm{CS}\mathrm{2}}$ to be ∼ 40 cm.

Figure 2 (a, c) Distribution of measured elevation differences (Δh) close to CS2 (a) and IS2 (c) intersecting satellite tracks within the entire study area (grey) and from intersecting tracks in areas with roughness higher (red) or lower (blue) than 2 m, respectively. Dashed lines are approximate normal distributions based on calculated median and nMAD. Only data from temporally close acquisitions are included. (b, d) For CS2 (b), a linear relationship (dashed violet line) exists between the logarithm to the local 100 m scale roughness and the estimated spatial uncertainty based on the dispersion of associated elevation differences (Eq. 1). For IS2 (d), on the other hand, we observe a linear correlation directly between the roughness and estimated spatial uncertainty. To ease the comparison between the derived CS2 and IS2 uncertainties, data from the other satellite are included in (b) and (d) (light grey). All uncertainty models are based on data from the summers of 2019 through 2022.

Spatial differences in CS2 observation uncertainties due to surface roughness are estimated accordingly: the logarithm to the local 100 m scale roughness is computed, and we apply the obtained linear relationship (Fig. 2b) while imposing a minimum uncertainty value of 0.39 m in areas of small surface roughness (< 1 m). The resulting distribution of the spatial uncertainty for the CS2 observations within our study area has a median value of 0.96 m (Fig. 3a; blue histogram).

It should be kept in mind that CS2 will preferentially sample the topographic highs located within the footprint, causing an inherent bias towards higher-elevation values. One consequence of this measurement bias is that the measured elevation differences obtained near the intersection of two satellite tracks may not reflect the full variability of the terrain over small distances. This will result in an underestimation of the observation uncertainty due to spatial variability, particularly in highly irregular terrain, and it is a likely cause behind the diminishing rate of increase in uncertainty at high roughness values.

Figure 3 Distribution of derived total uncertainties (grey), along with the individual spatial (blue) and temporal (green) uncertainty components for the CS2 (a) and IS2 (b) data, respectively. Data from summers 2019 through 2022.

4.1.2 Measurement and spatial uncertainty of the IS2 elevations

The measurement precision of the IS2 ATL06 product has been documented to be as small as 9 cm over the flat interior part of Antarctica (Brunt et al., 2019), and, compared to CS2, the ATLAS instrument provides much better resolved and localized elevation data with no topographic preference (Magruder et al., 2020). Hence, apart from outliers due to occasional errors in the ATL06 data caused by errors in tracking the surface within the photon cloud, the total observation uncertainty is dominated by the spatial and temporal variability of the surface elevation relative to the mean elevation field.

By construction, the 250 m median-averaged IS2 data used for DEM construction (Sect. 2.2) already include spatial averaging in the along-track dimension. However, spatial representability of the along-track-averaged values depends on the local topography; the precise location of the track will influence the resulting average more in areas of high topographic relief. Applying a similar approach to that for the CS2 observations, the uncertainty contribution from spatial representability of the IS2 observations is estimated by analysing the dispersion of measured elevation differences at temporally close adjacent observations near intersecting satellite tracks. Based on data from a total of 12 169 track intersections binned into 20 roughness intervals, we observe distinct differences to the derived CS2 uncertainties (see Sect. 4.1.1): for the IS2 data, the spread of the measured elevation differences is much smaller (Fig. 2c), and the spatial uncertainty increases linearly with the terrain roughness (Fig. 2d). At low roughness values (< 2 m), the uncertainty stabilizes at a 1σ value of ∼ 8 cm, consistent with the previously reported instrument measurement uncertainty for flat terrain (Brunt et al., 2019). The distribution of the individually estimated IS2 spatial uncertainties (Fig. 3b; blue histogram) has a median of 0.16 m.

4.1.3 Uncertainty due to temporal variability

To account for the changes in elevation during the observation acquisition period, a temporal uncertainty component is assigned to each of the observations based on its proximity to mid-summer (t₀, which we take to be the middle of the 4-month observation period, i.e. 1 August) and local long-term (2011–2020) average summer (May–August) elevation trends derived from CS2 altimetry (Slater et al., 2021a). The latter is important, since the rate of elevation change during summer is highly variable across the ice sheet (Slater et al., 2021b). We set σ_temp to be the absolute value of the local long-term average rate of summer elevation change multiplied by the time difference between acquisition time (t) and mid-summer:

$$\begin{array}{}\text{(2)}& {\mathit{\sigma }}_{\mathrm{temp}}=\left|{\left({\displaystyle \frac{\mathrm{d}h}{\mathrm{d}t}}\right)}_{\mathrm{summer}}\cdot (t-t_{\mathrm{0}})\right|.\end{array}$$

In areas not covered by data for average summer elevation trends, the average thinning of the ablation zone during the 2011–2020 period of 1.4 m yr⁻¹ (Slater et al., 2021b) is used.

The resulting distributions of temporal uncertainties for the individual CS2 and IS2 observations are illustrated in Fig. 3 (green histograms). Both distributions have a median of 0.07 m. The temporal uncertainty is generally less important than the spatial uncertainty component, particularly for CS2. However, the temporal uncertainty component may be non-negligible, with 21 % of the IS2 observations having larger temporal than spatial uncertainty. For CS2, this is only the case for 0.4 % of the observations.

4.1.4 Combined observation uncertainty

To obtain a measure for the total observation uncertainty, the spatial and temporal uncertainty components are combined in quadrature under the assumption that they are independent (Fig. 3, grey histograms). The derived observation uncertainties are subsequently tested for consistency with the observed elevation differences near intersecting satellite tracks. Computing Z scores from the observed elevation differences by dividing these by their estimated combined uncertainty, the resulting distributions are found to adequately approximate standard normal distributions, though heavier tails indicate the existence of outliers not fully captured by the estimated uncertainties.

The distributions of total observation uncertainty have a median value of 0.98 m (CS2) and 0.21 m (IS2), respectively. The derived uncertainties display large spatial variability, with much larger uncertainty towards the margin where the topography tends to be substantially rougher than in the smoother, and more temporally stable, inner part of the ice sheet marginal zone.

4.2 Bias estimation

Elevation measurements obtained from CS2 and IS2 over firn- and snow-covered surfaces may differ due to differences in penetration. However, because the PRODEMs are constructed for the ice sheet marginal zone during summer, where there is little snow and firn cover, we expect small biases only between the employed CS2 and IS2 altimetry within the PRODEM area. This assumption is verified by comparing temporally close IS2 and CS2 elevations near intersecting satellite tracks: based on observations from 8905 intersecting tracks from 2019 through 2022, the elevation differences are found to be distributed with a median value close to zero, suggesting no bias between measurements acquired by the two satellites. The median of the distribution tends to be smallest in magnitude in areas of low roughness (−0.05 m), where the elevation differences are best determined and the dispersion of the elevation difference distribution is small (Fig. 4). Only in areas of extreme roughness does the median elevation difference fall outside the 95 % confidence interval. This deviation from zero is only a fraction of the large (metre-scale) observation uncertainties within these areas (Fig. 2b, d), suggesting that this apparent bias may not reflect a true, systematic difference between the two elevation estimates.

The CS2 elevations overall tend to be slightly lower than the IS2 elevations, although this is not consistent across drainage basins. We consider the median value obtained for areas of low roughness (−0.05 m) to be an upper limit for the potential bias between the two altimeters over bare ice, since areas of flat terrain are predominantly located in the high-elevation inner part of the PRODEM region, which may periodically be covered by snow during the designated summer period. Values of similar range for the potential bias are found during leave-one-out cross-validation of the PRODEMs (Sect. 7.1; Table 2). This upper limit for a potential bias is well within the uncertainties of the CS2 observations (Fig. 3a). We therefore conclude that, in accordance with earlier studies (Dall et al., 2001; Davis and Moore, 1993; Otosaka et al., 2020), we do not observe any significant elevation bias between the two sets of altimetry in the PRODEM region within their associated uncertainties.

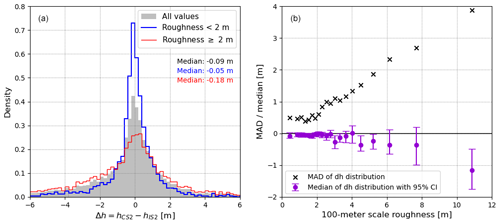
Figure 4 (a) Distribution of elevation differences, computed as $\mathrm{\Delta }h=h_{\mathrm{cs}\mathrm{2}}-h_{\mathrm{is}\mathrm{2}}$, near temporally close intersecting CS2 and IS2 satellite tracks. (b) Evolution of the median (violet dots) and MAD (black crosses) of the resulting elevation difference distribution as a function of the 100 m scale roughness of the terrain. The 95 % confidence interval (CI) on the median is computed using boot strapping. Data from the PRODEM area during summers 2019 through 2022.

5 Constructing the PRODEMs

5.1 Regional PRODEMs for marginal drainage basin subsectors

For computational purposes, we create regional PRODEMs for marginal subsectors based on drainage basin outlines, which are subsequently combined to form a full-margin DEM. We use the drainage basin definitions from Zwally et al. (2012), which divide the Greenland Ice Sheet into 19 drainage basins (Fig. 1). For each subsector DEM, data from a 10 km neighbourhood are included to avoid artefacts around drainage basin edges.

5.2 Elevation anomalies relative to ArcticDEM

Prior to interpolation, the satellite altimetry is detrended by subtracting a reference DEM (ArcticDEM v4.1) from each elevation measurement using linear interpolation. The resulting data set is labelled elevation anomalies. This is a standard pre-processing step prior to kriging (e.g. Dodd et al., 2015; Loonat et al., 2020) to ensure statistical robustness, as the method assumes stationarity of the mean field (see also Sect. 5.3). When using other methods to produce DEMs (e.g. Fan et al., 2022), such a processing step may not be a requirement. One advantage of this approach is that the elevation anomalies display a relatively smooth field valid for interpolation (Fig. 5). Even for areas with very rough terrain, such as those often found at the very outer part of the ice sheet edges, the observed elevation anomalies are consistent across length scales of 1–2 km (Fig. 5b).

Figure 5 Satellite altimetry from CS2 and IS2 after calculating the elevation anomalies to ArcticDEM for a marginal area in central west Greenland (red square in the overview map) with significant topographic relief. (a) The elevation anomalies (dh; coloured dots) display larger variability in the outer regions with the highest roughness (white areas), (b) but a zoomed-in view of an area with extreme topographic relief (square marked with a dashed red line in (a)) shows that even in these areas, the elevation anomalies are consistent across length scales of 1–2 km. IS2 observations can be recognized as data acquired along straight lines, while CS2 observations are geolocated according to the POCA. Data from 2019.

Based on the observed elevation anomalies relative to ArcticDEM, some outliers in the altimetry are clearly identifiable. The data are filtered by successively applying a 10×10 km spatial filter to the elevation anomaly data. Observations outside the 5σ range of local variability are identified as outliers and removed. The filtering is repeated 10 times, after which no or few outliers are detected. During the construction of PRODEM19, a total of 3.1 % of the CS2 data and 0.2 % of the IS2 data (together constituting 1.0 % of all data) are flagged as outliers. Further investigations show that many IS2 observations flagged as outliers are likely not measurement errors. The vast majority of these are located next to a nunatak, and the irregularity in elevation anomalies in these areas, as picked up by the spatial filter, is caused by large variability in the reference field obtained by linear interpolation of the 500 m resolution ArcticDEM to the measurement locations. In contrast, the CS2 observations flagged as outliers are evenly distributed throughout the study area, suggesting that these indeed represent inaccurate altimetry measurements, as caused by, for example, incorrect geolocation.

The PRODEMs are constructed using the same projection (EPSG:3413) and grid nodes as the ArcticDEM 500 m mosaic, thus avoiding additional interpolation when later adding the interpolated map of elevation anomalies to the reference DEM.

5.3 Spatial interpolation of the elevation anomaly field

The PRODEMs are spatially interpolated from the satellite altimetry point measurements by ordinary kriging (see, for example, Hengl, 2009). In essence, kriging performs an optimal unbiased linear prediction of a continuous field by exploiting knowledge of the spatial covariance of the field. The spatial covariance is specified in terms of a variogram, which can be extracted from the point cloud, and this information is subsequently used to assign distance-dependent weights to nearby data points. Several kriging variants exist. In ordinary kriging, the predictions are formed as the sum of a locally constant function and a spatially correlated stochastic field. Kriging can account for variable uncertainty of individual data points during the interpolation, and it is a widely used method to interpolate geophysical fields due to its robustness in capturing spatial variability (e.g. Bales et al., 2001; Bamber et al., 2001b; MacGregor et al., 2015).

Ordinary kriging relies on the data to be isotropic (i.e. have non-directional properties) and have second-order stationarity (i.e. with constant mean and variance fields) so that the spatial covariance structure is representative across the study space. While it is reasonable to assume the elevation field to be isotropic, neither the ice surface elevation field nor the elevation anomaly field relative to ArcticDEM is second-order stationary. Ice sheet surface elevations strongly violate the stationarity requirements, with mean elevations decreasing considerably towards the ice sheet margin, whereas the transformed data set of elevation anomalies does not show a similar trend. For neither data set, however, is the field variance stable across space: both the elevation and the elevation anomaly fields generally display higher variance in the topographically rough areas near the ice sheet margin than in the smoother inland areas.

Consequently, a single variogram cannot properly describe the spatial covariance of the elevation anomaly field relative to ArcticDEM. To account for this, we first estimate annual maps of the variogram parameters describing the varying spatial correlation structure of the elevation anomalies across the PRODEM area (Sect. 5.3.1). For a given location in the PRODEM grid, an appropriate set of variogram parameters is subsequently extracted and applied in the kriging routine (Sect. 5.3.2) to produce an interpolated value for the elevation anomaly. We call this method “regionally varying kriging”.

The final PRODEM is constructed by adding the map of derived elevation anomalies to the ArcticDEM mosaic, thereby forming an updated summer DEM for the region.

Under the assumption of Gaussian uncertainties on the input data, kriging can further employ the field's spatial characteristics to assess the uncertainty of the interpolated elevation field. The accuracy of the interpolated field will be limited if the number of sampled observations within the effective interpolation radius is small or if the sampled observations are inadequately distributed relative to the spatial properties of the field. Accuracy of the PRODEMs will therefore be reduced in areas of high variability and few observations, such as the conditions prevalent at the outer edges of the ice sheet.

5.3.1 Modelling the regionally varying spatial covariance structure

We first assess the varying spatial covariance structure of the elevation anomalies across the 50 km marginal ice sheet zone forming the PRODEM area. Spatial covariance may be represented by a variogram, which is a measure of half the variance of the differences in field value at two locations as function of the distance (“lag”) between those locations. To account for the spatially varying covariance structure of the elevation anomaly field, individual variograms are constructed for points in a 10 km grid covering the PRODEM area. The empirical variograms are computed using the Dowd estimator (Dowd, 1984; Mälicke et al., 2022; Mälicke, 2022), which is robust to extreme outliers.

From the point cloud of elevation anomalies, we observe that substantial changes in field characteristics sometimes take place over small spatial scales (< 5 km). Such rapid change occurs, for instance, in regions where a smooth low-elevation outlet glacier is surrounded by higher-elevation ice-covered mountainous areas, with the latter also displaying substantially higher spatial variability in the elevation anomalies. Nevertheless, to provide sufficient data for variogram estimation, we assume stationarity within a slightly larger area: each variogram is based on the nearest 2000 observations within a 30 km radius of the grid cell centre, the first condition generally being the most restrictive (mean distance to the observation furthest away is 20 km). We use 200 m binning of distance lags and a maximum bin size of 10 km, which generally ensures sufficient data for consistent retrieval of the variogram at all lags.

The empirical variograms are subsequently modelled using the exponential covariance function (Hengl, 2009). This is a widely used covariance model suitable for continuous spatial fields with relatively rapid changes and localized features, and it provides a good description of the various covariance structures existing within the elevation anomaly field. The exponential covariance function is given as

$$\begin{array}{}\text{(3)}& C\left(d\right)={\mathit{\sigma }}^{\mathrm{2}}\exp \left(-{\displaystyle \frac{d}{\mathit{\rho }}}\right).\end{array}$$

Here, C(d) is the covariance between two points separated by distance d, σ² is the variance of the field, and ρ is a length-scale parameter. The latter is a measure for how far an observation carries information on the surrounding field; the covariance of two points spaced with a distance of ρ is approximately one-third of the field variance. We define the effective range, L_e, as the distance after which two data points are essentially no longer correlated (covariance has decreased by 95 %), which can be calculated as L_e≈3ρ. For infinitesimal separation distances, a nugget effect (${\mathit{\sigma }}_n^{\mathrm{2}}$) may be added to the covariance function. The nugget represents measurement uncertainties and/or micro-scale variability in the data (natural variability at scales smaller than the sampling distance), both of which will cause two measurements at essentially the same location to differ slightly. In our case, a nugget will be present due to observation uncertainties, and we therefore prescribe the nugget based on the squared median uncertainty of the surrounding observations. Adding a nugget effect, a model for the variogram, γ(d), can be obtained from the covariance function by (see, for example, Hengl, 2009)

$$\begin{array}{}\text{(4)}& \mathit{\gamma }\left(d\right)={\mathit{\sigma }}^{\mathrm{2}}+{\mathit{\sigma }}_n^{\mathrm{2}}-C\left(d\right).\end{array}$$

An exponential variogram model is fitted using robust least squares to each of the empirical variograms in the coarse-resolution grid across the PRODEM area. The length scale, ρ, is constrained to the interval 500 m to 20 km (effective range: 1.5–60 km). No bounds are imposed for the variance. The predicted field values will tend to be dominated by many nearby observations carrying high weights in the interpolation, and it is therefore most important to correctly capture the covariance structure at close distances (small lags). To ensure that the fitted variogram models are well representing the covariance at small lags, these are weighted higher in the fitting procedure: applied weights are inversely proportional to the lag value of the empirical variogram. We further adjust the weights according to the number of observations at each lag, such that semi-variances calculated based on few observations are weighted less. With the general distribution of observations, this leads to approximately 50 % weighting at 5 km. Figure 6d–e show four examples of representative empirical variograms and fitted variogram models.

The procedure is repeated for each year in the PRODEM series. In the following, we focus on the variogram parameter fields obtained from summer 2019 data, but the overall patterns are consistent across the 4 years currently covered by the PRODEM series.

To avoid discontinuities in the final PRODEMs, the variogram parameter fields must be spatially continuous. Continuity of the variogram parameters is also expected since adjacent models are based on partly the same data set; the variograms are obtained for each point in the 10 km grid, with each variogram based on observations within a 30 km radius. To ensure continuity, the parameter fields are smoothed using a 3×3 pixel (i.e. 30×30 km) spatial median filter.

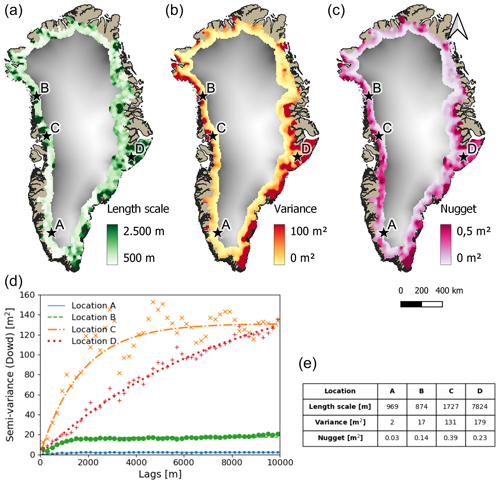
Figure 6 (a, b, c) Spatial variability across the PRODEM area of the three parameters of the exponential variogram model: length scale (a), variance (b), and nugget (c), respectively. The filtered parameters fields for 2019 data are shown. ArcticDEM ice surface elevations (greyscale) are used for background. (d) Four representative empirical and fitted variogram models found within the PRODEM area; locations are indicated with letters A–D in the maps. These are selected based on a K-means cluster analysis of the variogram parameters and selecting the variograms most representative of each cluster centre. (e) Table of variogram parameters corresponding to the modelled variograms shown in (d).

The large-scale patterns of variogram parameters (Fig. 6a–c) reflect the differences in spatial covariance across the marginal ice sheet zone. Elevation anomalies in the innermost part of the marginal zone are generally characterized by smooth fields, with low variance and small nugget values (Fig. 6, location A), implying that the elevation anomaly in these areas is very well characterized by nearby observations. The variograms here tend to display relatively small length scales, reflecting that local peaks and valleys exist within the otherwise smooth anomaly field. Moving towards the margin, the variograms gradually change towards higher variance and nugget values, but the length scale often remains small (Fig. 6, location B). Upstream outlet glaciers, we observe a varying pattern of high variance and nugget values, often combined with larger length scales (Fig. 6, locations C and D). Particularly, east Greenland outlet glaciers tend to be characterized by extremely high variance (location D).

For each PRODEM 500 m grid cell, an appropriate set of variogram model parameters is found by bilinear interpolation in the coarser parameter grid, and these are used as input to the kriging routine.

5.3.2 Interpolated fields of elevation anomalies and associated uncertainty

For each grid cell, the ordinary kriging interpolation is based on up to 200 nearby observations. The input data, however, are not distributed evenly, particularly given the closely spaced IS2 observations obtained along straight lines. To ensure that data included in the interpolation are well distributed, these data are selected by dividing the neighbourhood around the grid cell centre into eight subsectors and using the nearest 25 observations from within each subsector.

The expected field value at location x₀, here denoted $\widehat{f}\left(x_{\mathrm{0}}\right)$, can be calculated by weighting the surrounding J observations (x_i,z_i) according to their distance to x₀ using the local variogram function:

$$\begin{array}{}\text{(5)}& \widehat{f}\left(x_{\mathrm{0}}\right)=\mathit{\mu }+{\mathit{\lambda }}_{\mathrm{0}}^T\cdot \left(\mathit{z}-\mathit{\mu }\right).\end{array}$$

Here, z is a vector with the field observations, and λ₀ is a vector containing the weights for these at location x₀. We apply the local median of the observations as a robust estimator for the local mean value, μ, of the elevation anomaly field. The weights can be calculated by the following matrix equation (Paciorek, 2008):

$${\mathit{\lambda }}_{\mathrm{0}}={\left(\mathbf{C}+\mathbf{N}\right)}^{-\mathrm{1}}{\mathit{c}}_{\mathrm{0}},$$

where C is the covariance matrix between the J observations calculated based on their pair-wise distance using the local variogram parameters (Eq. 3), and c₀ is a vector for the covariance of the field at location x₀ and the various x_i. The total measurement noise and micro-scale variability for each observation are represented by the noise matrix N. This is a diagonal matrix whose entries on the diagonal are the squared observation uncertainties, i.e. N=ττ^T, with τ being the vector of observation uncertainties. To ensure that the weights sum to 1, an extra row and column are added to the kriging matrix equation, where the w₀ values are now the final kriging weights, and φ is the so-called Lagrange multiplier (Hengl, 2009):

$${\mathit{\lambda }}_{\mathrm{0}}{}^{\prime }=\left[\begin{array}{l}{\mathit{w}}_{\mathrm{0}}\\ -\mathit{\phi }\end{array}\right]={\left[\begin{array}{ll}\mathbf{C}+\mathbf{N}& \mathbf{1}\\ {\mathbf{1}}^T& \mathrm{0}\end{array}\right]}^{-\mathrm{1}}\left[\begin{array}{l}{\mathit{c}}_{\mathrm{0}}\\ \mathrm{1}\end{array}\right].$$

We also estimate the prediction uncertainty of the interpolated elevation anomaly field. The uncertainty primarily depends on the distance to (and uncertainty of) the nearest data points, along with the covariance structure informing on how much the field is correlated at those distances. Two kinds of uncertainties may be computed: the uncertainty of the underlying field value and the predictability of new data points obtained at the same location. The latter also accounts for the uncertainty associated with the micro-scale variability of the field and measurement uncertainties. The variance of the interpolated elevation anomaly field at location x₀ can be estimated as the weighted average of covariances between x₀ and all observation points x_i. Additional uncertainty from the Lagrangian correction term is adjusted for by adding its value (Hengl, 2009):

$$\begin{array}{}\text{(6)}& \mathrm{var}\left[\widehat{f}\left(x_{\mathrm{o}}\right)\right]={\mathit{\sigma }}^{\mathrm{2}}-{\mathit{c}}_{\mathrm{0}}^T\cdot {\mathit{w}}_{\mathrm{0}}+\mathit{\phi },\end{array}$$

with σ² being the local variance of the field, as determined from the local variogram. To estimate the variance of new observations z₀ obtained at the same location x₀, the observation uncertainty must also be addressed, and a nugget term is added to the equation (Paciorek, 2008):

$$\begin{array}{}\text{(7)}& \mathrm{var}\left[\widehat{z}\left(x_{\mathrm{o}}\right)\right]=\mathrm{var}\left[\widehat{f}\left(x_o\right)\right]+{\mathit{\sigma }}_n^{\mathrm{2}}.\end{array}$$

This is the uncertainty to be used for validating the resulting DEM (Sect. 7).

Applying the above equations using the previously determined spatially varying variogram parameters, we derive interpolated elevation anomalies (Eq. 5) and associated field variances (Eq. 6) at all PRODEM grid cell centres. To improve the estimation of the mean elevation anomaly across the grid cell, we subsequently smooth the elevation anomaly field by applying a 3×3 grid cell mean filter on the elevation anomalies obtained for grid cell centres. The resulting anomaly field and associated uncertainty are shown in Fig. 7a–b. For each grid point, we also apply Eq. (5) to derive the weighted average acquisition time of observations (in units of day of year) used in the elevation prediction (Fig. 7c). This provides an assessment of the average day during the 4-month summer period that the local interpolated elevation surface is most representative of, thereby providing a daily time stamp with each pixel in the DEM. This map of day-of-year values will be useful, for example, if generating elevation change maps by differencing individual PRODEMs.

Finally, the ArcticDEM 500 m mosaic is added to the obtained elevation anomaly field, forming an annual summer PRODEM for the marginal ice sheet zone (Fig. 7d). In a few places, the interpolated anomalies give rise to negative elevation values, which is unrealistic. This is caused by boundary effects; limited data lead to a retrieved constant elevation anomaly field in an area close to the ice sheet edge where ArcticDEM displays large variability. For these few areas, we correct the PRODEMs accordingly.

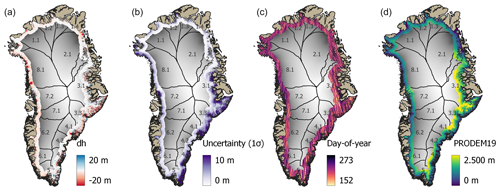
Figure 7 PRODEM19 results. (a) The resulting field elevation anomalies (dh) relative to ArcticDEM; (b) the associated uncertainty (1σ) on the interpolated field; (c) the weighted day of year of the interpolated surface, going from 1 June (day: 152) to 30 September (day: 273); and (d) the resulting PRODEM19 elevations. ArcticDEM elevations (greyscale) are used for background, with drainage basins indicated.

6 General attributes of the PRODEM series (2019–2022)

Figure 8 shows the distributions of PRODEM19 elevation anomalies relative to ArcticDEM (Fig. 8a), the uncertainty of the interpolated elevation fields (Fig. 8b), and the associated time stamp of the derived surfaces (Fig. 8c). Distributions are shown for the entire PRODEM area as well as for each major drainage basin. Over the current 4-year PRODEM series, the various distributions evolve, but the dominant patterns persist (Fig. 9).

The distribution of elevation anomalies (Fig. 8a) is distinctly leaning towards negative values (i.e. implying a general lowering of the surface relative to ArcticDEM) with a median value for the entire PRODEM area of −0.9 m (2019 values). The spread of the distribution of elevation anomalies is large, however, and with a heavy tail towards negative values indicating that large areas in the PRODEMs have considerably lower elevations than ArcticDEM. We attribute this to an actual surface lowering of the ice sheet that has taken place throughout and subsequent to the acquisition period (2007–2022) of stereo imagery utilized for generating ArcticDEM. Spatially, negative anomalies (decreased elevations) dominate the west Greenland marginal areas (Fig. 8a; green curves), while regions with positive anomalies (increased elevations) are more common in east Greenland (Fig. 8a; blue curves), as can also be seen from Fig. 7a. For all drainage basins, however, the median elevation anomaly is negative.

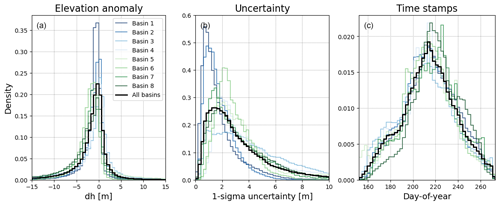
Figure 8 Distribution of (a) PRODEM19 elevation anomalies to ArcticDEM, (b) uncertainties (1 standard deviation) on the PRODEM19 elevation field, and (c) weighted day of year of the altimetry used as input for the interpolation. Histograms are shown for the entire PRODEM area (black lines) as well as individually for all major drainage basins, with blue colours for drainage basins in north and east Greenland and green colours for basins in south and west Greenland. Colour saturation is relative to basin latitude.

The overall spatial patterns are stable over time. The median value of the elevation anomaly distribution for a drainage basin may change over time, often showing a decreasing trend (indicative of overall decreasing elevations), but the differences between values for individual drainage basins are significantly larger than the change over time within a single basin (Fig. 9a).

A map of the accumulated elevation change since 2019 can be calculated by comparing the spatial map of elevations (or elevation anomalies) to the corresponding 2019 values ($\mathrm{\Delta }{h}_{\mathrm{year};\mathrm{2019}}=h_{\mathrm{year}}-h_{\mathrm{2019}}=\mathrm{d}{h}_{\mathrm{year}}-\mathrm{d}{h}_{\mathrm{2019}}$). The median of the Δh_year;2019 distribution across the entire PRODEM area shows a steady elevation decrease amounting to a total average decrease of 0.6 m from summer 2019 to summer 2022 (Fig. 9b). The southern and southeastern drainage basins display the strongest decreasing trend, with elevations on average decreasing by 1.8 m (basin 5) and 1.3 m (basin 4). The northern and western regions (drainage basins 1, 6, 7, and 8) also tend to experience substantial decreases in elevation of between 0.4 to 0.9 m. Conversely, surface elevations in marginal northeast Greenland (basins 2 and 3) show little total elevation change over the PRODEM period. This is primarily due to a substantial increase in surface elevations within these regions from summer 2021 to 2022, the year during which the southern and southeastern basins (basins 5 and 6) experience the strongest decrease in surface elevation. These general spatial trends are in line with those previously reported in the literature (e.g. Sørensen et al., 2018; Zwally et al., 2011), but the PRODEMs allow the temporal aspect of these changes to be investigated in much higher detail than was previously possible. We furthermore observe that the heterogeneity is high within each region, with areas of increasing and decreasing surface elevations existing side by side. To summarize, while surface elevations in the marginal areas of the Greenland Ice Sheet have generally been decreasing since 2019 across almost all regions and all years, the magnitude of change shows large spatial and annual variability, as the spatial pattern of change is complex and overlaid with substantial inter-annual variations.

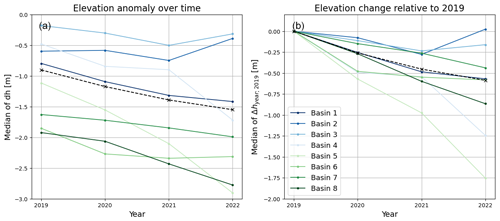
Figure 9 (a) Evolution in median elevation anomaly relative to ArcticDEM over the PRODEM period (2019–2022) and (b) evolution in median of the total elevation change relative to 2019 over the PRODEM period. Values are given both on drainage-basin scale (coloured from blue to green, with blue being marginal drainage basins in north and east Greenland and green being basins along the south and west Greenland coast; darker colours correspond to higher latitudes) and for the entire PRODEM area (dashed black line).

Figure 10 Distribution of PRODEM19 prediction errors of the elevation anomaly after removal of either one track of CS2 data or one track (consisting of three beams) of IS2 data. (a) Distribution of prediction errors prior to normalization. (b, c) Distribution of prediction errors when normalized relative to the estimated 1σ uncertainty of the interpolated field and the observation uncertainty of the validation data. For both distributions, the associated normal distributions are also shown, based on calculating the median and normalized MAD of the prediction errors (solid coloured lines), as well as using the mean and standard deviation (dashed coloured lines). The standard normal distribution (solid black line) is shown for comparison. (d) Normal probability plots comparing the quantiles of the prediction error distributions with those of the standard normal distribution. Deviations from a straight line (black) indicate departures from normality.

Areas with limited data availability result in increased uncertainty of the interpolated surface. The median 1σ uncertainty of the PRODEM19 elevation anomaly field (and hence also the PRODEM19 elevations) is 2.6 m with a mode of 1.4 m (Fig. 8b). Similar values are obtained for subsequent years. However, the distribution has an extended tail towards higher values, implying that some areas cannot be interpolated very accurately based on the available data. For all years, this is particularly an issue for drainage basin 3, for which an exceptionally long tail exists, corresponding to an extended area of relatively large uncertainties. Given denser data close to the pole due to the satellite orbits, the uncertainty generally decreases towards the north.

7 Validation of the PRODEMs

We assess the robustness of the PRODEMs through two complementary approaches: block leave-one-out cross-validation (block LOO-CV) and validation of PRODEM19 against an external data set. Block LOO-CV (Sect. 7.1) provides an internal assessment of the product by iteratively interpolating the elevation anomaly field based on all but data from a single track and subsequently testing on the omitted sample. This method supports validation across the entire PRODEM area, providing estimates of the product performance with respect to the input data. Due to its large-scale coverage, the distribution of prediction errors obtained from the block LOO-CV supports analysis of the spatial error structure, shedding light on the product limitations and potential areas for improvement (Sect. 7.2).

Validation against an independent external data set offers an additional layer of verification, as it allows potential biases or inconsistencies to be identified that are inherent in the original data set. However, independent validation data from the PRODEM region and period are sparse. In Sect. 7.3, we evaluate the PRODEM19 product performance against a single CryoSat Validation EXperiment (CryoVEX) flight line of airborne laser scanner data acquired in August 2019 covering a short section across the northeast Greenland Ice Sheet margin (Hvidegaard et al., 2021).

Table 1 Parameters describing the distribution of prediction errors after cross-validation based on successive removal with replacement of one track of CS2 or IS2 data, respectively, for each year in the current PRODEM series.

7.1 Block leave-one-out cross-validation

Validating the PRODEMs using block LOO-CV, we iteratively remove one track of either CS2 or IS2 data (one IS2 track consisting of all beams), as these are correlated. We limit the number of repetitions to 50 times maximum for each basin, after which the results are found to stabilize. On average, one track of removed data corresponds to 0.5 % (CS2) and 1.8 % (IS2) of the total data set within a basin. The prediction errors (Fig. 10a) are subsequently normalized (Fig. 10b, c) relative to the predicted standard deviation of new observations obtained at the given locations (Eq. 7) combined with the uncertainty of the data used for validation (Sect. 4). If elevations are well estimated within their associated uncertainties, the normalized prediction errors should be distributed according to the standard normal distribution.

Table 2 Parameters describing the distribution of normalized prediction errors after cross-validation based on successive removal with replacement of one track of CS2 or IS2 data, respectively, for each year in the current PRODEM series. In the ideal case, the normalized prediction errors should form a standard normal distribution, e.g. median and mean value (μ) equal to 0 and nMAD and standard deviation (σ) equal to 1, with 68 % of the data falling within ±1 of the distribution (central region with σ=1). For both satellites and all years, the distribution of normalized prediction errors shows good consistency with these values.

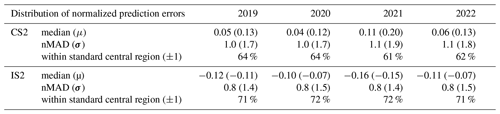
Figure 10b–c show the normalized prediction error distributions for PRODEM19 after successive removal with resampling of one track of CS2 and IS2 data, respectively, within each drainage basin. Prior to normalization, the prediction error distributions are strongly peaking around 0 m (Fig. 10a; Table 1), with median values close to 0 m and nMAD around 2 m. After normalization, however, both sets of normalized prediction errors are reasonably well described by the standard normal distribution, suggesting that large prediction errors tend to be associated with large prediction uncertainties (Table 2). Similar results are obtained for subsequent years in the PRODEM series, and on average 63 % (CS2) and 72 % (IS2) of the predicted elevations fall within their associated 1σ uncertainty interval. The slightly lower percentage obtained for the CS2 prediction errors than theoretically expected (68 %) may partly be due to remaining uncertainties in the CS2 validation data. With the prediction errors of the elevation fields well distributed according to the prediction uncertainty, we conclude that the PRODEMs within their associated uncertainties generally provide a good description of the true elevation fields.

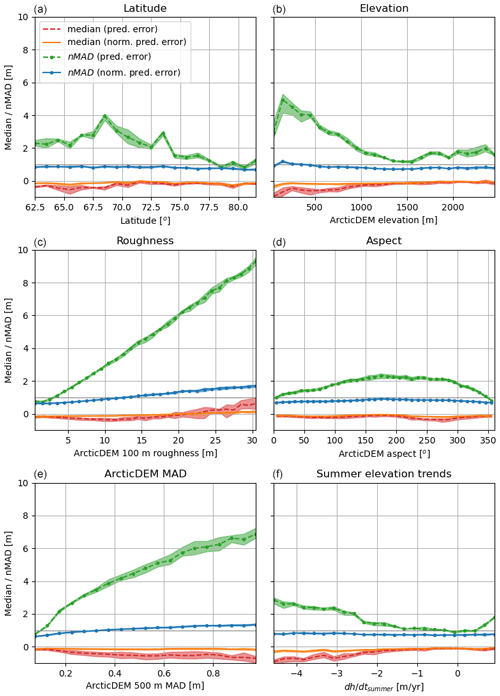
Figure 11 Descriptive measures (median and nMAD) of the distribution of PRODEM raw (dashed lines) and normalized prediction errors (solid lines), when stratified relative to various location and terrain properties that may impact the PRODEM product performance: (a) latitude, (b) elevation, (c) roughness, (d) aspect, (e) uncertainty of ArcticDEM, and (f) summer elevation trends. Lines correspond to mean values over the 4-year PRODEM series, with the envelope showing minimum and maximum values for the 4 years. Bins are created to cover the 5 to 95 percentiles of each data set. The ArcticDEM MAD value is the median absolute deviation of the DEMs contributing to ArcticDEM at a given location, thereby providing an elevation uncertainty estimate. Summer elevation trends from Slater et al. (2021a).

The analysis, however, also identifies some limitations with the reported uncertainties: all distributions display higher central peaks and significantly heavier tails than a standard normal distribution (Fig. 10d). The higher peaks imply that uncertainties tend to be overestimated. The heavier tails, on the other hand, indicate that the reported uncertainties do not capture the full range of variability and that, for a small percentage of the data, uncertainties are severely underestimated. A potential explanation for the heavy tails is the assumption that the uncertainty associated with the input observations conforms to a Gaussian distribution. This assumption of normality is, at best, an approximation. The observed elevation difference distributions near intersecting satellite tracks employed for assessing the observation uncertainty show a much higher central tendency and heavier tails than a normal distribution, particularly in areas of high roughness (Fig. 2a, c). We hypothesize that the heavy tails of the observation uncertainty distributions are carried over to the interpolated field.

The distribution of prediction errors, raw as well as normalized, display slight differences depending on which set of satellite observations is used for validation. We consider the prediction errors based on validation against the more accurate IS2 data to best reflect the elevation field uncertainties and base the following analysis on these (Sect. 7.2). The IS2 normalized prediction errors (Fig. 10c) are slightly more centrally distributed, indicating the reported uncertainties to be more conservative. We observe that depending on which data set is used for validation, there is a tendency towards a slight overestimation (for CS2) or underestimation (for IS2) of the observed elevations. This feature is fairly consistent across years and drainage basins, albeit with large regional differences in magnitude, and it is likely due to the construction of the PRODEMs from two sensors that may interact slightly differently with remaining snow-/firn-covered surfaces within the PRODEM area (see Sect. 4.2).

7.2 Analysis of the PRODEM error structure

7.2.1 Predictive capability of PRODEMs depending on location and terrain properties

While the block LOO-CV shows that the PRODEM elevation fields overall are well described within the prediction uncertainties, the product performance varies spatially depending on the physical location and terrain properties. We stratify the PRODEM IS2 prediction errors (raw as well as normalized) relative to the following parameters: location (latitude, longitude), elevation, roughness, slope, aspect, uncertainty of ArcticDEM, and long-term trends in summer elevation (Fig. 11). Elevation, aspect, slope, and ArcticDEM uncertainty are based on the 500 m resolution ArcticDEM mosaic; roughness is based on the 100 m resolution ArcticDEM mosaic; and long-term summer elevation trends are from Slater et al. (2021a). For most parameters, the errors are well characterized by the reported uncertainties. As an example, the dispersion of the prediction error distribution tends to decrease with increasing latitude (due to denser data coverage), whereas the dispersion of normalized prediction errors stays relatively constant around unity (Fig. 11a). No significant relationship exists between prediction errors and longitude (not shown).

Figure 12 Directional variograms showing the spatial correlation structure of IS2 block LOO-CV prediction errors in the along-track and across-track directions. In the across-track direction, the variogram has a small length scale, indicating that in this direction errors are essentially uncorrelated. Based on data from 2019.

The largest prediction errors are found in areas of rough terrain (Fig. 11c): the errors linearly increase with terrain roughness, attaining nMAD values of the error distribution of up to 10 m in areas of extreme roughness (ArcticDEM 100 m scale roughness values of 30 m, roughly corresponding to the 95th percentile of the roughness field within the PRODEM area). This is not unexpected; at such high roughness it is difficult to properly interpolate an average 500 m elevation field, and the data used for interpolation are often limited to IS2, since CS2 does not provide good measurements in such terrain. A similar relationship is found for the slope (not shown). The prediction errors also reach increasingly high values as the ArcticDEM uncertainty increases (Fig. 11e). As the ArcticDEM mosaic is used as a reference during PRODEM construction, it is not surprising that these uncertainties will propagate to the PRODEMs. In order of decreasing importance, the prediction errors also tend to be higher in areas of low elevation (Fig. 11b), for areas displaying large negative trends in elevation over the summer (Fig. 11f), and for south-facing slopes (i.e. aspect ∼ 180°; Fig. 11d).

The analysis allows us to identify problematic areas, where one should be cautious about the reported PRODEM uncertainties. These are characterized by having nMAD values of the normalized prediction uncertainties significantly above unity, which we define here as larger than 1.2. This is the case for areas with roughness above 17 m and/or ArcticDEM MAD values above 0.65 m. The first condition covers 18 % of the PRODEM area, while the second condition covers 13 %, and they largely overlap in the areas along the edge of the ice sheet (in 24 % of the PRODEM area, at least one of the conditions is met).

7.2.2 Spatial correlation of errors

The errors of the PRODEM elevation fields are not randomly distributed. In addition to the influence of location and varying terrain properties (Sect. 7.1.1), we observe a spatial correlation in the error structure. A main reason for this is that the observations are acquired at different times during the summer, during which the surface elevation may change non-negligibly due to surface mass balance processes. Consequently, areas with closely spaced IS2 tracks acquired early and late in the season may result in stripes in the resulting DEM (see Sect. 9.3).

To gain an understanding of the spatial structure of the elevation prediction field, we analyse the spatial correlation of the IS2 prediction errors. Since the error structure is likely to be aligned with the satellite tracks (in particular the straight lines of IS2 observations), we construct directional variograms along and across the IS2 track directions. We again compute the empirical variograms using the Dowd estimator (Mälicke et al., 2022). As the track direction is location dependent, the analysis is done for each basin individually (both for ascending and descending tracks), and the basin-scale variograms are averaged by taking the median of the semi-variances before fitting an exponential variogram without nugget to the results. In the along-track direction, the error structure has an effective correlation length of about 3 km (length scale: 1000 m), whereas the variogram for errors in the across-track direction displays a small length scale (335 m), indicating that errors are essentially uncorrelated in this direction (Fig. 12).

7.3 Validation of PRODEM19 against airborne laser-scanner measurements

Independent validation data are sparse because airborne altimetry campaigns usually take place in spring, i.e. outside the PRODEM period. In 2019, however, the ESA CryoVEx/ICESat-2 spring campaign suffered from bad weather, and, as a result, an airborne summer measurement campaign with a laser scanner set-up was conducted in August 2019 (Hvidegaard et al., 2021). The focus of this campaign was sea ice in the Wandel Sea, northeast of Greenland, but one flight line captured on 10 August (ALS_20190810T151333_164135 (ESA, 2022)) also covers a section of land ice, thus providing independent airborne laser scanner (ALS) data (Fig. 13).

We first down-sample by averaging the very high resolution CryoVEX ALS data to 10 m grid resolution and filter them to only contain ice surface observations. Subsequently, we average all ALS ice elevations within each PRODEM grid cell and compute the difference to the gridded PRODEM19 elevation value. Statistics for the resulting distribution of elevation differences (Δh) are provided in Table 3. While this is the most direct way to compute the elevation differences, it does, however, not account for uncertainties related to the number and distribution of ALS data within a grid cell. We therefore also compare against a reduced ALS data set constructed with additional scrutiny regarding the number of observations used to produce the gridded ALS elevations: we remove ALS average elevations in the 10 m resolution grid based on fewer than five observations, and after subsequent downsampling to the PRODEM 500 m resolution grid, averages based on fewer than 50 contributing elevation measurements are removed. This causes a slight reduction of the available grid cell values to be used for comparison, but it removes a significant number of outliers, leading to less dispersion of the elevation difference distribution. Another way to account for a potential uneven distribution of ALS observations across the PRODEM grid cells is by computing the elevation differences based on anomalies to ArcticDEM (Δdh), thereby adjusting for the local slope: a 10 m gridded set of ALS elevation anomalies is computed, followed by downsampling to the PRODEM grid. The ALS elevation anomalies are subsequently compared to the PRODEM elevation anomalies. This approach gives rise to substantially less dispersion of the observed elevation difference distribution.

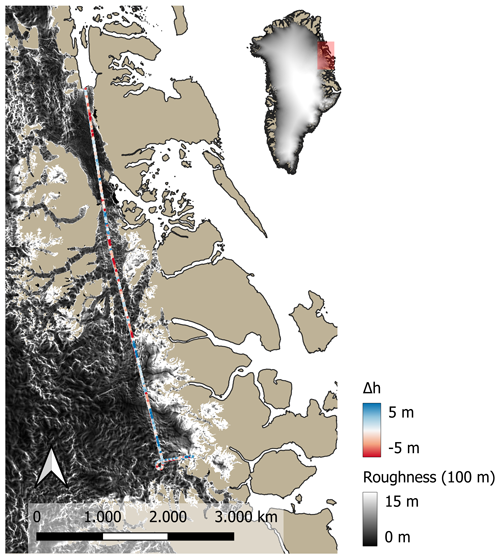
Figure 13 Location of the CryoVEX ALS flight line from August 2019 and the gridded ice surface elevation differences of PRODEM19 to the ALS data (Δh). ArcticDEM 100 m scale roughness is used as background (greyscale).

Regardless of the approach, the differences between ALS and PRODEM19 elevations are small (Table 3). The statistics slightly improve when removing gridded ALS data based on limited observations and when conducting the analysis on the difference in elevation anomalies rather than the elevations directly.

Table 3 Statistics for comparison of elevations (raw and normalized) in PRODEM19 and CryoVEX ALS data from northeast Greenland acquired on 10 August 2019. The ALS data are first down-sampled to the PRODEM grid. Standard deviation (SD) and root-mean-square error (RMSE) are calculated as SD = $\sqrt{\frac{\sum {\left(\mathrm{\Delta }h-\mathrm{mean}\right)}^{\mathrm{2}}}{N-\mathrm{1}}}$ and RMSE = $\sqrt{\frac{\sum \mathrm{\Delta }{h}^{\mathrm{2}}}{N-\mathrm{1}}}$, where N is the number of cells.

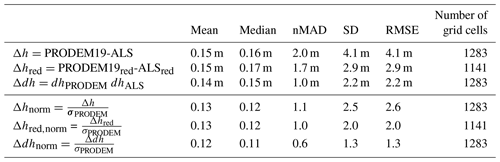
The ALS flight line crosses areas of varying roughness (Fig. 13), including areas of high topographic relief associated with substantial PRODEM elevation uncertainties. Using a similar approach as for the block LOO-CV prediction errors (Sect. 7.1), we therefore also investigate the distribution of normalized errors, i.e. the elevation differences divided by the local PRODEM elevation field uncertainty. The resulting distributions are close to a standard normal distribution (Table 3), implying that PRODEM19 provides a good estimate of the elevation field within the stated uncertainties.

8 Comparison to an IS2-only Greenland DEM obtained for the period 2018-19

Very few large-scale DEMs exist for the Greenland Ice Sheet that are valid for the PRODEM period. The exception is a recently constructed DEM, in the following abbreviated IS2DEM19, derived from IS2 data from its first year of operation (November 2018 to November 2019) (Fan et al., 2022). It has a nominal resolution of 500 m, and it is developed based on a spatio-temporal fitting model. For several reasons we do not expect the IS2DEM19 to be identical to PRODEM19. A significant difference is that IS2DEM is based on data from an entire year, during which the surface elevations evolve with the seasons. A larger snowpack during the winter season is expected to result in generally higher elevations in IS2DEM19 than in PRODEM19. This is corroborated by a comparison of the two elevation fields; their median elevation difference across the marginal ice sheet zone is −2.0 m, indicating that PRODEM19 tends to display lower elevations. However, substantial variability in the elevation differences is observed across the area.

Further, the PRODEMs are derived as elevation anomalies to ArcticDEM, whereas such an approach has not been taken for IS2DEM19. Looking at the small-scale features of the DEMs, this difference in approach becomes evident, with many of the fine-scale features existing in ArcticDEM being preserved in the PRODEM elevations (albeit in a modified form). As a result of its smoother appearance, the slope distribution of IS2DEM19 tends towards smaller values than PRODEM19 and ArcticDEM, the latter two having almost identical slope distributions (Fig. 14h).

Figure 14 shows how the large- and fine-scale structures differ between the three DEMs (PRODEM19, IS2DEM19, and ArcticDEM v4.1) for Petermann Gletsjer in northern Greenland. Their differences are visible directly from the elevation field (e–g), but they become even more evident from the spatial patterns of elevation differences to PRODEM19 (b–d) and slope (j–l). The fine-scale structure of PRODEM19 is fairly similar to that of ArcticDEM, whereas its large-scale field is more similar to IS2DEM19. This is especially evident for an area in the outer part of the glacier tongue, where both PRODEM19 and IS2DEM19 display substantially higher elevations than ArcticDEM, suggesting that the glacier front has advanced since acquisition of the ArcticDEM elevation field. The resemblance between the PRODEM19 and IS2DEM19 elevation models is improved by first smoothing PRODEM19 with a Gaussian filter (Fig. 14b), after which the median difference between the two elevation fields slightly decreases (median difference for the marginal ice sheet zone: −1.9 m). Compared to IS2DEM19, the increased resolution of fine-scale features in the PRODEMs comes at the cost, however, of additional assumptions regarding the stability over time of the small-scale structure of the elevation field.

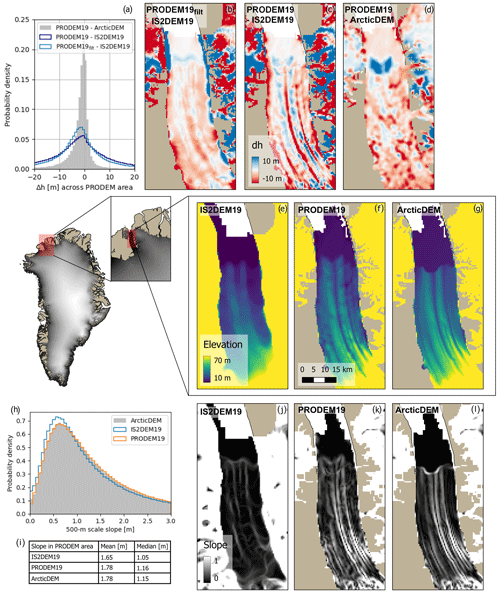
Figure 14 A comparison of the three elevation fields: IS2DEM19, PRODEM19 (including a filtered version; PRODEM19_filt), and ArcticDEM across Petermann Gletsjer. PRODEM19_filt is produced by applying a Gaussian filter with a radius of 5 pixels and relative standard deviation of 50 %. Coverage of the three DEMs differs slightly across the region. (a) A histogram of the distribution of elevation differences across the PRODEM area. (b–d) Maps showing the spatial distribution of elevation differences of PRODEM19 versus IS2DEM19 and ArcticDEM, respectively, across Petermann Gletsjer, along with a comparison of elevation differences between PRODEM19_filt and IS2DEM9. (e–g) The elevation fields across Petermann Gletsjer. (h) Distribution of slopes across the entire PRODEM area, along with (i) a table of mean and median values of the slope distributions. (j–l) The spatial distribution of slope for the three elevation models across Petermann Gletsjer.

9 Discussion

9.1 Impact of data sparsity on PRODEM elevation accuracy

For a reliable outcome of kriging, the field to be interpolated must be quasi-stationary, and hence it is a prerequisite to use a reference DEM to produce elevation anomalies for interpolation. Our approach has the advantage of inheriting the detailed elevation from ArcticDEM to also maintain the high spatial resolution of the PRODEMs in areas poorly covered by the satellite altimetry. Regardless of data coverage, the employed approach acts to add small-scale topographic features visible in ArcticDEM, with the underlying assumption that these are stable over time.

Ideally, the altimetry data should exhibit spatial variability representative of the elevation anomaly field, capturing both local fluctuations and broader trends. This will ensure that the kriging interpolation for every grid cell is based on a sufficiently large set of representative samples. Based on the spatial correlation structure of the elevation anomalies, we can evaluate the number of observations that significantly contribute to the interpolated PRODEM elevation fields, i.e. observations located within a radius corresponding to the effective length scale of the local variogram. On average, the interpolated field is based on 78 nearby observations (median of the distribution; 2019 values) (Fig. 15). In 2019, a total of 4 % of the PRODEM grid cells suffer from sparsity in neighbouring data, which we take to be fewer than five observations within the local effective length scale. For 2 % of the grid cells, no observations exist within this interpolation radius. Slightly improved values are obtained for the subsequent years; PRODEM22 has the most well-determined elevation field, with fewer than 2 % of the grid cells suffering from sparse data (< 1 % without any nearby observations). The issue of data sparsity is most pronounced in the southern regions; for the southernmost drainage basin (basin 5) the percentage with sparse data coverage has increased to 14 % (7 % without any nearby observations) (2019 values). In regions without any nearby observations, the ArcticDEM elevations are simply adjusted with a constant depending on the median value of the local anomaly field, as calculated from the 200 closest altimetry observations. Consequently, the PRODEMs are in these areas heavily reliant on the quality of ArcticDEM.

Figure 15 Distribution of the number of altimetry observations within the interpolation radius for the PRODEM grid cells. The interpolation radius corresponds to the local effective length scale (roughly equivalent to 3 times the length scale for the exponential variogram model) for the elevation anomaly field. Histograms are provided for the individual drainage basins (coloured from blue to green, with blue being marginal drainage basins in north and east Greenland and green being basins along the south and west Greenland coast; darker colours correspond to higher latitudes) and for the entire PRODEM area (black line). Data are from 2019, which is the year when data sparsity is most pronounced.

9.2 The PRODEM anomaly fields reveal artefacts in ArcticDEM

ArcticDEM is a multi-year elevation model that incorporates stereo photogrammetry from an extended period, during which the ice sheet topography has evolved. This leads to artefacts in the product, which become apparent in the interpolated elevation anomaly fields. Due to ArcticDEM being constructed as a mosaic of 100×100 km tiles, with each tile separately registered to reference elevations from GrIMP DEM v2, the PRODEM elevation anomalies display a checkerboard pattern, with each tile having a slightly different mean value. This is, for example, the case for an area in central west Greenland (Fig. 16), where the distribution of anomalies in the northern tile (Fig. 16, tile a) is −7.5 m ± 7.9 m, whereas the distribution in the adjacent southern tile (Fig. 16, tile b) is −0.3 m ± 9.7 m (PRODEM19 values). As apparent from this artificial checkerboard pattern, the derived field of elevation anomalies to ArcticDEM does not represent varying rates of elevation change rates.

Figure 16 The PRODEM elevation anomalies (here for PRODEM19) relative to ArcticDEM display a checkerboard pattern due to the way ArcticDEM was constructed. Two ArcticDEM tiles of 100×100 km are indicated.

9.3 Striped patterns in PRODEMs due to seasonal elevation changes

Like ArcticDEM, the PRODEMs display artefacts caused by temporal differences in data acquisition, albeit on significantly shorter timescales, resulting in less time for surface changes to occur. The PRODEM altimetry is collected during a 4-month period, during which the surface elevation may change due to, for example, snowfall and surface melt. As a result, we in some areas observe a striped pattern in the interpolated PRODEM elevation anomaly field, seemingly aligned with the IS2 satellite tracks (Fig. 17a–b). The differences in the elevation anomaly field across the stripes are on the order of half a metre or less and within the uncertainty of the interpolation.

Investigating the source of this pattern, we observe that it often occurs where two closely spaced IS2 satellite tracks are obtained at the beginning and end of the summer season, respectively. Indeed, the IS2 observations along the two tracks may differ in average elevation by up to a metre. For the area between the satellite tracks, the interpolated surface depends on which line of observations is closest. This can also be seen from the varying weighted mean acquisition time of the input data used in the interpolation across the area: a striped pattern similar to that in the elevation anomalies is evident from the day-of-year field (Fig. 17c). However, not all locations with large variability in average time of data acquisition are prone to form this stripy pattern. The pattern is only visible in areas where the surface elevation has changed significantly during the summer period and where the spatial correlation of the elevation anomaly field is characterized by a short length scale, causing the closest data points to be given a high weight during interpolation.

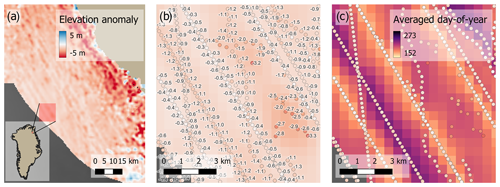
Figure 17 A striped pattern in the PRODEM elevation anomaly fields is caused by differences in time of data acquisition. (a) 2019 elevation anomalies in a small area of northeast Greenland (red box in the overview figure). (b) A zoomed-in view (red box in a) of the elevation anomaly field to an even smaller area. Dots indicate the altimetry on which the interpolation is based. The data are labelled and coloured according to the measured elevation anomaly (same colour scale as the interpolated field). (c) Averaged day of year represented by the interpolated surface, going from 1 June (day: 152) to 30 September (day: 273) in 2019. The coloured dots represent the measured elevation anomalies.

10 Data availability

The PRODEMs described in this paper can be accessed at https://doi.org/10.22008/FK2/52WWHG (Winstrup, 2024), with the paper based on the second release (rel2) of the data set. The annual 500 m resolution DEMs follow the naming convention PRODEMyy, with yy indicating the year. Presently, the product covers summers 2019 through 2022. The product is expected to be updated annually over the coming years.

Each annual 500 m resolution PRODEM is provided as a georeferenced raster in GeoTIFF-format (.tif). The rasters are in the National Snow and Ice Data Center (NSIDC) Sea Ice Polar Stereographic North projection and referenced to the WGS84 datum (EPSG:3413). Each PRODEM contains the following four data layers:

• DEM – PRODEMyy (heights above the WGS84 reference ellipsoid, in m),

• variance – elevation uncertainty (field variance, in m²),

• dh – elevation anomalies (m) relative to the ArcticDEM v4.1 500 m mosaic,

• time stamp – time stamp associated with the interpolation (in units of day of year).

11 Conclusions

We have constructed an annual series of 500 m resolution summer DEMs (PRODEMyy) for the marginal zone of the Greenland Ice Sheet. The DEMs are created by fusing satellite altimetry data from CryoSat-2 and ICESat-2, and hence the PRODEM series starts in 2019, the first summer after ICESat-2 became operational. ArcticDEM v4.1 is employed as a reference DEM, which ensures that high spatial resolution is also maintained in areas with limited altimetry. The present PRODEM series consists of four DEMs, with the most current being from summer 2022, and we aim to repeat the procedure for the coming years to continually obtain annual changes in surface elevation across this rapidly changing region of the Greenland Ice Sheet.

The PRODEMs are interpolated using regionally varying kriging on elevation anomalies relative to ArcticDEM, in an approach that may also be applicable for interpolation of other semi-stationary fields. Spatially varying uncertainties of the individual observations are modelled based on analysing observed elevation differences close to intersecting satellite tracks. The applied approach is able to account for the large regional differences in observational uncertainty and covariance structure of the anomaly field across the area. The PRODEMs are validated using block leave-one-out cross-validation, and the obtained elevation fields are found to be well determined within their associated spatially varying uncertainties. In most cases, the uncertainties are slightly conservative, but there is a higher number of outliers than predicted by a Gaussian distribution. The PRODEMs are best determined in the northern regions, where the data coverage is most dense, and lesser so in areas with very high roughness. PRODEM19 is additionally validated against data from one flight line with an airborne laser scanner, and we find very good agreement between the two data sets.

For most of the marginal zone, we observe a lowering of the ice sheet surface compared to ArcticDEM, albeit with large spatial differences. However, since ArcticDEM is built from data from a regionally varying time window, the elevation differences between the PRODEMs and ArcticDEM cannot be directly converted to elevation change estimates. Indeed, some features in the elevation anomaly field merely reflect artefacts related to the construction of ArcticDEM in tiles: we observe a checkerboard pattern in the derived elevation anomalies, with each tile having distinctly different mean anomaly values.

Over recent years, the surface of the Greenland Ice Sheet has been experiencing a general lowering due to climate change, and a complex and annually shifting pattern of changes is superimposed on this trend due to glacier dynamics and mass balance processes. In almost all regions of the marginal ice sheet, we observe a thinning of the ice sheet, most so in the south and southeastern marginal areas of the Greenland Ice Sheet, where the average surface elevation has decreased by more than 1 m over the 4-year PRODEM period. The exception is the marginal areas of northeast Greenland, which from summer 2021 to 2022 experienced a substantial increase in elevation, causing the average surface elevation to almost be stable over the PRODEM period. By capturing the patterns of change in the marginal ice topography on an annual basis, the PRODEMs will give valuable insights into the inter-annual variability of ice sheet dynamic processes and contribute to the validation of ice sheet models.