the Creative Commons Attribution 4.0 License.
the Creative Commons Attribution 4.0 License.
A focal mechanism catalogue of earthquakes that occurred in the southeastern Alps and surrounding areas from 1928–2019
Monica Sugan
Gianni Bressan
Gianfranco Renner
Andrea Restivo
We present a focal mechanism catalogue of earthquakes that occurred in the southeastern Alps and surrounding areas from 1928 to 2019. The area involved in the process of convergence between the Adria microplate and Eurasia is one of the most seismically active regions in the Alpine Belt. The seismicity is minor, with the Ms= 6.5 Friuli earthquake being the strongest event recorded in the area, but the seismic risk is relevant because it is a highly populated region. For this reason, numerous studies have been carried out over time to investigate the stress field and the geodynamic characteristics of the region using focal mechanisms. To provide a comprehensive set of revised information, which is challenging to build quickly because the data are dispersed over many papers, we collected and revised the focal mechanisms that were previously published in the literature. Additionally, depending on the data quality and availability, we computed new focal mechanisms by first arrival polarity inversion or seismic moment tensor. Finally, we merged all the fault plane solutions to obtain a catalogue for a selection of 772 earthquakes with . For each earthquake, we reported all the available focal mechanisms obtained by different authors. We also suggested a preferred solution for users who need information provided expeditiously.
The catalogue (https://doi.org/10.5281/zenodo.4660412; Saraò et al., 2021) is given as the Supplement of this paper and will be updated periodically (https://doi.org/10.5281/zenodo.4284970).
- Article
(4187 KB) - Full-text XML
-
Supplement
(5496 KB) - BibTeX
- EndNote
The focal mechanisms, or fault plane solutions (FPSs), describe the orientation of the fault on which an earthquake occurs and the direction of the slip. FPSs allow for an understanding of seismotectonic processes through the study of the stress field of a region and are essential for seismic hazard assessment.
The first methods to determine the FPS (Knopoff and Gilbert, 1960) were based on observations of the polarity of the first P-wave motion at stations placed at known distances and azimuths from the source.
After the 1980s, with the development of digital broadband instruments, FPSs computed by seismic moment tensors became very popular (e.g. Gilbert, 1970; Dziewonski et al., 1981). In general, the point source is located at the hypocentre, except for models that make use of the source centroid. The difference between the location of the initiation of rupture and the centroid can be significant, except for that of small earthquakes (Dziewonski and Woodhouse, 1983). For this reason, FPSs computed by polarities or by moment tensors might produce different results due not only to systematic errors or inadequacies in the velocity models. Mechanisms by polarities represent the geometry of the fault at the initial breaking of the rupture, while the moment tensor provides the source mechanism of the dominant component of the rupture geometry. Additionally, the differences between the two methods become relevant when the source deviates by the approximation of a pure double couple, for instance when fluids play an essential role in earthquake generation. However, despite their limits – such as inadequacies in the P- and S-wave velocity models and poor station coverage, together with erroneous polarity readings that may result in large deviations between the model solution and the actual fault planes – the focal mechanisms obtained using first-motion polarities are still computed and used. For small to moderate earthquakes (i.e. aftershock sequences), they are often the only source information available obtained using local network data (Shearer, 1998; Lentas et al., 2019).
At present, almost all seismological observatories compute quick moment tensors for earthquakes above a certain threshold of magnitude and publish solutions on dedicated online platforms. The Global Centroid Moment Tensor (CMT) project (Dziewonski et al., 1981; Ekström et al., 2012), the National Earthquake Information Center (NEIC) of the USGS (Benz, 2017), and the GEOFON data centre (2020) report moment tensor solutions for world seismicity and thresholds of magnitudes of about Mw 5.0, Mw 5.5, and Mw 4.5, respectively. In addition to these, there are also many regional or local moment tensor catalogues with magnitude thresholds of about Mw 3.6 (e.g. Scognamiglio et al., 2006, Time Domain Moment Tensor catalogue – TDMT; Kubo et al., 2002, NIED seismic moment tensor catalogue) and Mw 4.5 (e.g. Pondrelli and Salimbeni, 2015, Regional Centroid Moment Tensor Catalog – RCMT). Furthermore, some online databases, such as the bulletin of the International Seismological Centre (Lentas et al., 2019) and the database of the Stress World Map project (Zoback, 1992; Heidbach et al., 2018), contain both polarities and moment tensor FPSs of global seismicity.
In the past, FPSs were computed and published in specific studies investigating the geodynamics of selected regions. These studies are still being performed today to revise the preliminary FPS or calculate the FPS of events of M<4.0. Several authors have put considerable effort into researching FPSs reported in many papers and collecting them in catalogues for specific areas to provide a set of revised information, which is often challenging to build quickly. It is important to stress that collecting data, which are very often spread in different documents and locations, checking and selecting parameters, and standardizing the information is a long and painstaking job, which is sometimes not fully recognized.
For European areas, in addition to the first compilations of Constantinescu et al. (1966), McKenzie (1972), and Udías et al. (1989), more recent catalogues include the EMMA database (Vannucci and Gasperini, 2004), which collects the focal mechanisms of earthquakes that occurred in the Mediterranean area from 1905 to 2006 in the range . In several cases, after merging the available FPSs for an earthquake, the authors assess and suggest a preferred solution based on different priorities or strategies (e.g. Gerner, 1995; Radulian et al., 2002; Custódio et al., 2016; Kapetanidis and Kassaras, 2019).
In this study, we present a new catalogue of FPSs of earthquakes that occurred in the southeastern Alps and surrounding areas from 1928 to 2019 (Supplement and Saraò et al., 2021). Because of the relevant seismic hazard in the region (e.g. Slejko et al., 1998; Meletti et al., 2021) and its importance from a geodynamical point of view, many authors have computed the FPS of earthquakes that occurred in this area using different data and different techniques (e.g. Anderson and Jackson, 1987; Slejko et al., 1989, 1999; Del Ben et al., 1991; Herak et al., 1995; Bernardis et al., 1997; Aoudia et al., 2000; Pondrelli et al., 2001; Poli and Renner 2004; Danesi et al., 2015; Viganò et al., 2008; Bressan et al., 2007, 2009; 2018; Pondrelli and Salimbeni, 2015; Restivo et al., 2016; Romano et al., 2019). A significant boost in seismological studies occurred after the devastating 1976 Friuli earthquake (Ms= 6.5), the strongest earthquake recorded in instrumental times in northeastern Italy (Slejko, 2018, and references therein). In addition to the main shocks, the most energetic aftershocks (e.g. Slejko et al., 1989, 1999; Poli et al., 2002) were analysed to understand the geodynamic process occurring in the region; most of the FPSs of the Friuli sequence were calculated manually using a graphical method. Subsequently, with the use of computer techniques (Whitcomb, 1973; Reasenberg and Oppenheimer, 1985), many other small earthquakes belonging to seismic sequences (e.g. Bernardis et al., 1997; Bressan et al., 2009, 2018) were carefully investigated to understand the stress regime of the area (e.g. Bressan et al., 2003, 2007, 2009, 2018). In recent times, Aoudia et al. (2000) and Pondrelli et al. (2001) reviewed the mechanisms of 1976 main shocks in terms of the moment tensor, and since 2006, the moment tensor has been routinely computed for earthquakes of M≥3.6 in the region (e.g. Scognamiglio et al., 2009; Saraò, 2016).
The aim of our study is to collect and revise all the FPSs published over time in a comprehensive catalogue. Additionally, we employed a set of first polarity data collected by an author before data exchange via the Internet and read in person from the seismograms of selected observatories. These data were used to compute FPSs manually in previous studies, but only portions of them were published. We use the datasets to recalculate the FPSs based on current knowledge (Sugan et al., 2020). The new solutions are then merged with the FPSs found in the literature. Depending on the data availability and quality, we compiled a dataset with the FPSs computed for 772 selected earthquakes (Supplement and Saraò et al., 2021). In the following section, we describe the study area, the methodologies, and data used to build our catalogue and outline its main characteristics.
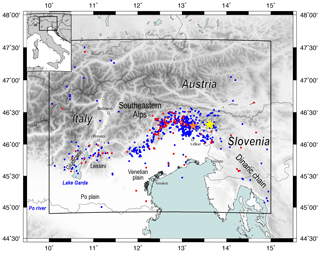
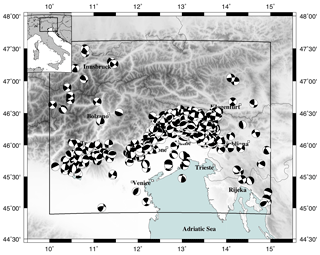
Figure 1Map of the epicentres of the focal mechanisms reported in the catalogue (Saraò et al., 2021) presented in this paper. The epicentres of the focal mechanisms retrieved from the literature are indicated by the blue dots, and the newly computed FPSs are indicated by the red dots. The 1976 Friuli earthquake (orange star) and the 1998 and 2004 Bovec earthquakes (yellow stars) are also shown. The map was generated by GMT software (Wessel et al., 2019).
The region that we considered in this study (Fig. 1) is bounded by Lake Garda to the west, western Slovenia to the east, the Venetian Po Plain to the south, and Austria to the north (latitude 45–47.5∘ N and longitude 10–15∘ E). The area is one of the most seismically active regions of the Alpine Belt and is involved in the convergence between the Adria microplate and Eurasia (e.g. Battaglia et al., 2004; D'Agostino et al., 2005, 2008; Serpelloni et al., 2005). The rates of convergence increase from west to the east by up to 1.5 to 2.0 mm yr−1 (D'Agostino et al., 2005). The structural setting is a complex system resulting from the superposition of several tectonic phases that have generated a NW–SE-trending Dinaric chain (to the east) and E–W-trending Alpine faults (southeastern Alps). In the west, the Giudicarie–Lessini region is a crucial zone for geodynamics, and it represents a tectonic boundary between the central western and southeastern Alps with an orientation transverse to the strike of the Alpine chain (Viganò et al., 2015).
The National Institute of Oceanography and Applied Geophysics (OGS) northeastern Italy seismic and deformation network (Priolo et al., 2005; Bragato et al., 2011, 2021) has monitored the study region since 1977, complemented since 2002 by a GNSS network (Zuliani et al., 2018). Several studies (e.g. Gentili et al., 2011; Peruzza et al., 2015; Sandron et al., 2018) provide a general description of the data recorded, including the main variations of the OGS northeastern Italy seismic network (OX) geometry over time, the acquisition mode, and the type of seismographs.
The seismicity, mainly located in the upper crust (Bressan et al., 2018, 2019; Viganò et al., 2015), is minor and directly related to the deformation along the western margin of the Adriatic indentation (Gentili et al., 2011; Romano et al., 2019). Rovida et al. (2020) reported that approximately 30 earthquakes of occurred in historical times, and the largest main shocks (M>5.0) instrumentally recorded after the 1976 Ms= 6.5 Friuli earthquakes (e.g. Aoudia et al., 2000) occurred in 1998 (Ms= 5.7) and 2004 (Mw=5.1) in the Bovec area (e.g. Bajc et al., 2001; Kastelic et al., 2008; Bressan et al., 2009) (Fig. 1).
3.1 FPSs from the literature
The FPSs from the literature were obtained after careful research; the found FPSs were thoroughly checked for typos and orthogonality of the nodal planes as well as for the compatibility of pressure and tension axes with the nodal planes according to the Aki and Richards (1980) convention. The Aki and Richards (1980) convention defines the two planes by the strike, measured clockwise from the north with the fault dipping down to the right of the strike direction, and the dip, measured down from the horizontal. The rake is the angle between the strike direction and slip, with slip taken as the direction of the hanging wall relative to the footwall. Because the two planes are orthogonal, the three angles defining one plane also define the orientation of the second plane. The orientations of the pressure (P) and tension (T) axes, located in the centre of the dilatational and compressional quadrants, respectively, are given by the azimuth (0–360∘, north = 0∘, east = 90∘) and the plunge (0–90∘, down from the horizontal).
Starting with the published nodal planes, we recomputed the solutions to check their consistency and to add, when missing, a uniform dataset of parameters for each event. Whenever possible, we cross-checked the corrected solutions with the author or the beach ball shown in the original publication. We did not include the solutions for which it was impossible to recover consistent planes starting from the available information in the catalogue. In the case of multiple FPSs for the same earthquake, we considered all of them. However, when the FPSs were copied from one paper to another by different authors, we reported the FPSs referred to in the first article in which they appeared. If the same authors published slightly different FPSs for the same earthquake, we considered only the FPS of the most recent publication.
3.2 The new computed FPS
Before computing the FPS, we relocated the earthquakes using Hypo71 (Lee and Lahr, 1975), a standard location procedure, and the 1D layered velocity model (Riggio and Russi, 1984; Bressan et al., 2003) used for the analysis of the earthquake reported in the Friuli Venezia Giulia Seismometric Network Bulletin (Centro di Ricerche Sismologiche – CRS, 2020). The model has a P-wave velocity (Vp) = 5.85 km s−1 from the surface down to a depth of 22 km, a Vp = 6.8 km s−1 from 22 to 39.5 km of depth, and a Vp = 8 km s−1 for the half-space. The P- to S-wave velocity ratio is 1.78.
To estimate the FPS by polarities, we used the FPFIT algorithm (Reasenberg and Oppenheimer, 1985), which is based on a grid-search procedure that finds the strike, dip, and rake of the two planes by minimizing a normalized weighted sum of the first-motion polarity discrepancies. The misfit function (zero perfect fit, one complete misfit) is computed from the number of inconsistent polarities and weighted by the quality of the observation and the distance from the nodal planes. For some events, the inversion algorithm provided multiple solutions as a result of an insufficient number of polarity readings, the presence of polarity misreading, the inclusion of localization errors, or the use of an inadequate velocity model. In such cases, we selected the preferred solution based on (a) the data distribution on the focal sphere relative to the radiation pattern (i.e. the number of first-motion polarities – Fm ≥ 10; station distribution ratio – STDR ≥ 0.4; misfit ≤ 0.3) and (b) agreement with the tectonic lineaments and style of the epicentral area.
The first polarities used to compute the FPSs were manually picked from seismograms or extracted from the bulletin of the International Seismological Centre and the Seismological Bulletin of Slovenia. The polarities were also read from the seismograms archived in various Italian and European seismological observatories, many of which are no longer operating (Osservatorio meteorico-sismico nel Seminario – Chiavari; ENEL, Osservatorio Ximeniano – Florence, Osservatorio Astronomico “Brera” – Milan, Dipartimento di Fisica dell'Università di Padova – Padua, Osservatorio S. Domenico – Prato, Osservatorio meteoro-sismico nel Santuario di N.S. – Oropa, Osservatorio Bina – Perugia, Osservatorio “Valerio” – Pesaro, Osservatorio meteorico-sismico nel Collegio Alberoni – Piacenza, Osservatorio Meteorico Istituto Fisica – University of Siena, Sismografi Lungo Periodo di Mantovani (Bologna, Bolzano, Grosseto, Naples, Olbia, Palermo, Turin), Osservatorio meteorico-sismico nel Seminario Maggiore – Treviso, Osservatorio meteorico-sismico nel Seminario Patriarcale – Venice, Ljubljana, Munich, Stuttgart, Vienna).
After 1977, the first-motion polarities were also picked from the seismograms recorded by the network managed by OGS and integrated with the data recorded by the surrounding seismic networks. For data recorded since 2006, we used the digital seismograms acquired by the OX network to compute the seismic moment tensor for earthquakes of ML≥3.6 that occurred in NE Italy and the immediate surroundings (Bragato et al., 2021; Saraò, 2006, 2020). Using the TDMT code by Dreger (2003), an algorithm widely employed in several observatories worldwide (e.g. Kubo et al., 2002; Clinton et al., 2006; Scognamiglio et al., 2009), we inverted the seismic waveforms in the frequency range of 0.02–0.05 Hz. A cross-correlation function was used to align data with Green's functions computed by the algorithm of Saikia (1984). This level of approximation afforded a great level of flexibility in rapid source parameter determinations when the event locations and the origin time are preliminary (Dreger and Helmberger, 1993; Dreger et al., 1998). The source depth is estimated iteratively by finding the solution that yields the highest variance reduction (VR). VR is an index of the waveform fit between observed and synthetic seismograms and is given by the sum of squares of the difference in amplitude normalized by the observed waveforms (100 % is the best). Kubo et al. (2002) showed that stable and reliable solutions are obtained for VR greater than 50 %.
Noisy or nodal stations and inadequate structural models can result in inaccurate moment tensor estimates. For this reason, Saraò (2007) performed a feasibility study to calibrate and tune the algorithm for the investigated area in relation to the station geometry and to the local velocity model employed (Bressan, 2005), finding the best parameter configuration that allows robust estimates of the best double couple orientation and of the Mw value.
3.3 Merging the new FPSs with the published ones
Although we reported all the available FPSs for an earthquake in the catalogue, both retrieved from the literature and newly computed, we indicated a preferred one based on the following priority criteria: (1) the solution was computed within this study; (2) the fault plane solution was determined by moment tensor; (3) the solution was computed within the framework of a detailed study of the area and possibly after accurate relocation of the hypocentre (in both these cases, each fault plane solution was validated for data quality and distribution); (4) the solution is the latest computation; (5) the solution is compatible with our knowledge of the main tectonic features of the area; (6) the solution is part of a regional catalogue; and (7) the solution is compatible with most of the solutions proposed by independent studies. It was impossible to select the best solution based on the quality parameters of the FPS computation because such parameters were computed in a heterogeneous way and are provided sporadically.
To account for the variability of the preferred solution and the alternative ones (i.e. solutions of other authors) for the same event, we computed the 3D rotation angle by which one double couple was rotated into another arbitrary couple (Kagan, 1991). The Kagan angle varies between 0∘ for identical solutions and 120∘ for the absolute mismatches. Pairs of solutions with an angle below 20–30∘ were considered very similar (Nakamura et al., 2016; Lentas et al., 2019).
We used the software FMC (Álvarez-Gómez, 2019), which includes subroutines from Gasperini and Vannucci (2003), to verify and classify all the focal mechanisms in our catalogue. The fault type was classified by seven types of double couple classification (N: normal; N-SS: normal – strike-slip; SS-N: strike-slip – normal; SS: strike-slip; SS-R: strike-slip – reverse; R-SS: reverse – strike-slip; R: reverse) similar to the conceptual geological classification of faults (Álvarez-Gómez, 2019). To provide thorough information and facilitate easy inclusion in other databases, we also reported the classification adopted by the World Stress Map project (Zoback, 1992). This classified the events into five types (N, N-SS, SS, R-SS, R), and those not fitting in any of the five types were placed in the unknown category.
We report in our catalogue 987 fault plane solutions for 772 earthquakes (Fig. 2) with a magnitude range of (Supplement and Saraò et al., 2021). For each earthquake, we report the latitude and longitude of the epicentre, origin time, focal depth, magnitude, the strike, dip, and rake of the two nodal planes, azimuth and plunge of the P, T, and B axes, fault type (using both Álvarez-Gómez, 2019, and Zoback, 1992, classifications), and associated references. In the case of multiple solutions, we indicate the preferred Kagan angle and the classification according to the priority code described in the previous section.
Table 1Parameters of the new FPSs computed by first-motion polarities (Sugan et al., 2020). Here we report the following: date (yyyy-mm-dd), time (hh:mm:ss), lat. (latitude north in degrees) and long. (longitude east in degrees), depth (km; * indicates fixed), M (magnitude), Str1, Dip1, and Rak1 (strike, dip, and rake of the first fault plane in degrees), Str2, Dip2, and Rak2 (strike, dip, and rake of the second fault plane in degrees), Ft (fault type according to Zoback, 1992), Fm (number of first-motion polarities), STDR (station distribution ratio), and misfit. Other details are given in the full catalogue (Supplement and Saraò et al., 2021).
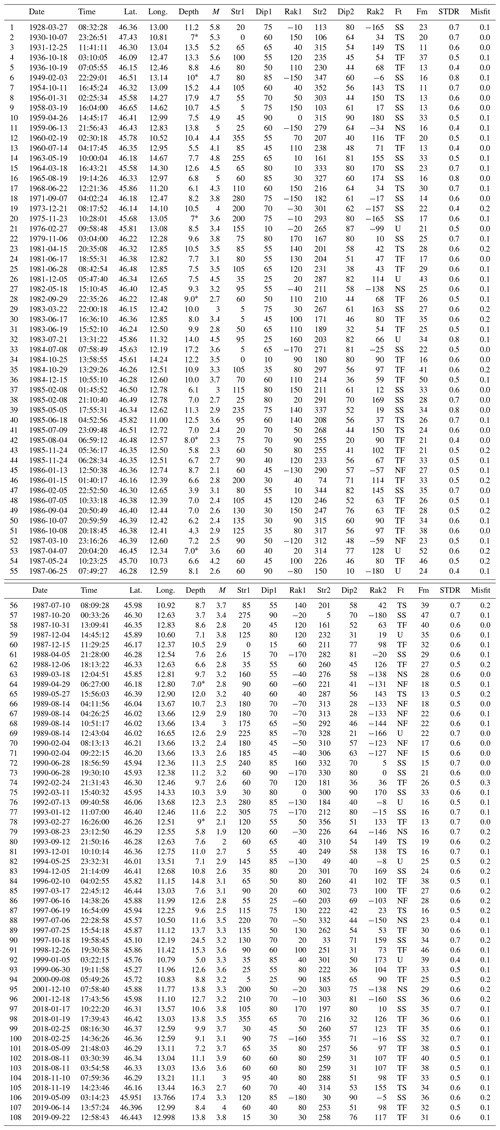
Table 2Parameters of the new focal mechanism solutions computed by the moment tensor (Saraò, 2020): date (yyyy-mm-dd), time (hh:mm:ss), lat. (latitude north in degrees) and long. (longitude east in degrees), depth (km), Ml (local magnitude), MD (duration magnitude), Mw (moment magnitude), Mo (seismic moment), Str1, Dip1, and Rak1 (strike, dip, and rake of the first fault plane in degrees), Str2, Dip2, and Rak2 (strike, dip, and rake of the second fault plane in degrees), Ft (fault type according to Zoback 1992), and Q (quality inversion parameter; 4 is the best solution). Other details are given in the full catalogue (Supplement and Saraò et al., 2021).
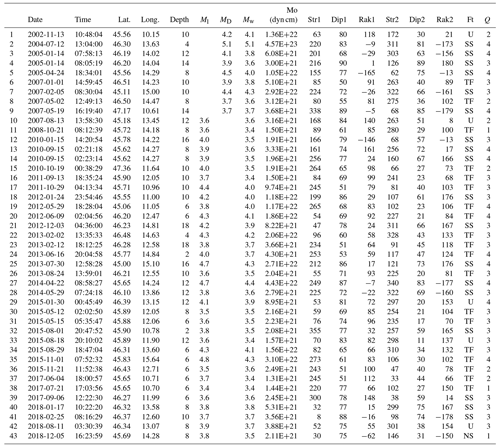
We collected and revised from the literature 836 FPSs (85 % of the whole catalogue), 68 of which have been corrected with respect to the original information, while for 428 we added the values missing to obtain a uniform dataset of information. For each solution, the changes reported are commented on in the database. Of the 151 newly computed focal mechanisms reported in the catalogue, the FPSs of 108 earthquakes with occurring between 1928 and 2019 are computed by first-motion polarities (Table 1, Sugan et al., 2020, for details of the input data and inversion results), and 43 FPSs of earthquakes with occurring from 2002 to 2018 are computed by moment tensor (Table 2, Saraò, 2020, for details of the solutions).
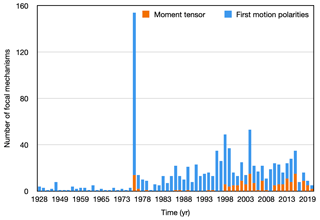
Figure 3Distribution in time of the fault plane solutions using a 1-year bin (year vs. number of fault plane solutions).
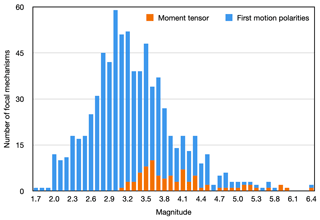
The focal mechanisms are provided only for selected earthquakes based on data availability and quality. For this reason, the distribution in time and magnitude of the mechanisms in our catalogue may be uneven and linked to the study case of specific earthquakes and particular seismic sequences. Looking at the temporal distribution of the FPSs of our catalogue (Fig. 3), we observe peaks in seismicity following the 1976 Ms= 6.5 Friuli earthquake, 1998 Ms=5.7 earthquake (Bajc et al., 2001), and 2004 Mw=5.1 Bovec earthquakes (e.g. Bressan et al., 2007, 2009). The increasing number of focal mechanisms soon after the 1976 Friuli earthquake was boosted both by data coming from temporary stations (Slejko et al., 1999) and by the development of the OGS network that has since then made it possible to investigate low-energy earthquakes (M<3.5). The magnitude of the computed FPSs ranges from 1.8 to 6.5, but most of the fault plane solutions have been computed in the magnitude range of 2.8 to 3.5 (Fig. 4).
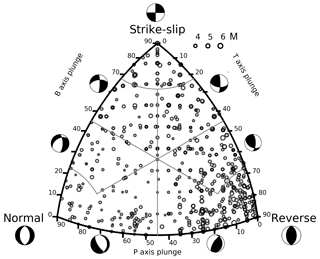
Figure 5Focal mechanism classification of our catalogue plotted on a ternary diagram (Kaverina et al., 1996).
The ternary diagram in Fig. 5 shows the fault type distribution of the 772 preferred FPSs contained in our catalogue, while the pie plots (Fig. 6a, b) show the percentage of fault type mechanisms obtained by the two approaches to classify the mechanisms. The classification by Álvarez-Gómez (2019, Fig. 6a) accurately characterizes seismic earthquakes with different strike-slip components. Reverse mechanisms are a feature of the area under investigation, but the presence of strike-slip solutions is also relevant and in agreement with the different kinematic regimes that characterize the region from east to west. Previous studies (e.g. Slejko et al., 1999; Poli et al., 2002; Bressan et al., 2018) have shown that thrust faulting is the dominant mechanism in the southeastern Alps, with a significant presence of strike-slip events, while strike-slip faulting prevails in the Dinaric domain. Viganò et al. (2015) found that thrust faults with a strike-slip component and strike-slip faults prevail in the western sector, confirming that the seismotectonic zones Giudicarie and Lessini are undergoing different kinematic regimes.
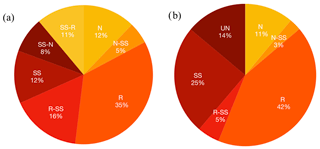
Figure 6(a) Classification of the focal mechanism according to Álvarez-Gómez (2019) and (b) Zoback (1992). N: normal; N-SS: normal – strike-slip; SS-N: strike-slip – normal; SS: strike-slip; SS-R: strike-slip – reverse; R-SS: reverse – strike-slip; R: reverse; UN: unknown.
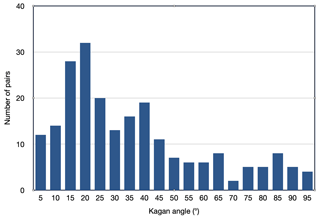
Figure 7Kagan angle between the preferred solution and the alternative FPSs reported in our catalogue.
In Fig. 7, we plot the Kagan angle to show the difference between our preferred solutions and the other FPSs available for the same earthquake. Although many pairs of focal mechanisms are below 20–30∘, there are discrepancies above 30∘. The observed trend is not surprising and has been found for other datasets with multiple earthquake source solutions (e.g. Ishibe et al., 2014; Nakamura et al., 2016; Lentas et al., 2019) due to the differences in data and methods used to compute the solution for the same earthquake over time.
From the comparison of the solutions computed in this study with solutions already published, we observe some agreement but also some discrepancies that are likely due to the different configuration parameters used to locate the events, the different datasets used as input, and the diverse techniques employed.
For instance, the location of the 1928 Ms= 5.8 Tolmezzo earthquake, the oldest event in our dataset (Table 1), is different from that in previous studies (e.g. Slejko et al., 1989; Sandron et al., 2018). It is more compatible with the location reported in the macroseismic Italian database and the associated catalogue (Locati et al., 2016; Rovida et al., 2020, 2021) as well as with the seismogenic features of the area than before (Bressan et al., 2018). Recently, Rovida et al. (2021) have revised the magnitude for this event to be equal to 6.08. The retrieved focal mechanism is a strike-slip type, confirming the solutions previously found by other authors (e.g. Slejko et al., 1989; Cagnetti et al., 1976), probably because of the low impact of the hypocentral location when using data from very far-field stations, as were used in this case.
It is worth mentioning the results obtained for the 1936 Ms= 5.6 Alpago Cansiglio earthquake (Table 2), whose causative fault is still controversial (Galadini et al., 2005; Sugan and Peruzza, 2011). We obtained two possible FPSs (Sugan et al., 2020): one with a strike-slip component, as previously found by others (e.g. Peruzza et al., 1989), and one with a compressive solution compatible within the uncertainties with the mechanism obtained by Sirovich and Pettenati (2004) using the regional macroseismic intensity pattern. We suggest the compressive solution as the preferred one and hypothesize that the new solution can shed new light on the study of this earthquake being compatible with a known fault segment (Aviano Thrust outcropping) along the Cansiglio mountain front (Galadini et al., 2005).
The catalogue of focal mechanisms described in this paper is given as the Supplement of this paper and it is also available in CSV format on Zenodo (https://doi.org/10.5281/zenodo.4660412, Saraò et al., 2021).
The first-motion dataset used to compute the focal mechanisms is available on Zenodo (https://doi.org/10.5281/zenodo.4284929, Sugan et al., 2020).
The seismic data used to compute the seismic moment tensor are provided by the OGS northeastern Italy seismic network (OX) at https://doi.org/10.7914/SN/OX (last access: 17 May 2021, OGS, Istituto Nazionale Di Oceanografia E Di Geofisica Sperimentale, 2016). The waveforms can be downloaded from the European Integrated Data Archive EIDA (http://www.orfeus-eu.org/data/eida/, last access: 17 May 2021, EIDA Italia Node, 2021).
The GMT software (Wessel et al., 2019) was used to generate the maps.
We compiled a comprehensive catalogue of 987 focal mechanisms for 772 selected earthquakes of that occurred in the southeastern Alps and surrounding areas from 1928 to 2019 (Supplement and Saraò et al., 2021). The study region represents a key area from a geodynamic point of view and is characterized by significant seismic risk. For such reasons, many authors have investigated the seismicity of this region and computed many focal mechanisms. In the catalogue, we have collected and revised 836 published solutions to provide a homogeneous and high-quality dataset of focal mechanisms; 68 have been corrected for typos or inconsistencies, and, whenever possible, the corrected solutions have been discussed with the author or checked against the available details in the paper. Additionally, we have enhanced and made available the set of polarity readings of past earthquakes that would otherwise be lost; thus, we computed 108 new FPSs of earthquakes that occurred between 1928 and 2019 using a set of peak polarity readings that were not used or published before for certain reasons (Sugan et al., 2020) and 43 earthquakes with that occurred from 2002 to 2018 by moment tensor (Saraò, 2020).
The distribution in time and magnitude of the FPSs are correlated with the study cases of specific earthquakes (e.g. 1976 Ms= 6.5 Friuli earthquake, 1998 Ms= 5.7, and 2004 Mw= 5.1 Bovec earthquakes) and relevant seismic sequences occurring in the area. Thrust faulting is the dominant mechanism of our catalogue, with a significant presence of strike-slip events and a minor presence of normal faults. In the catalogue, we report all the FPSs available for each earthquake, and we suggest a preferred FPS for users who need to quickly have information to roughly represent the area at the current state of knowledge. By the Kagan angle, we quantify the difference among the preferred solutions and other solutions to provide additional insights to the end user. If the differences are well within the uncertainties for the majority of focal mechanism pairs, the discrepancy might be relevant for some other cases.
Our catalogue will be upgraded yearly with the FPSs of the most recent earthquakes occurring in the area (https://doi.org/10.5281/zenodo.4284970) to maintain the published dataset as up to date and complete as possible.
The supplement related to this article is available online at: https://doi.org/10.5194/essd-13-2245-2021-supplement.
AS designed the experiment. AS and MS wrote the paper, prepared the figures, and revised the FPSs collected from the literature. MS, GB, GF, and AR read the first arrival peaks and computed the new FPSs by polarities. AS computed the FPSs by moment tensor. GB provided comments on the paper.
The authors declare that they have no conflict of interest.
We acknowledge the colleagues in the Seismological Research Centre at the OGS for continuous effort in maintaining the OGS northeastern Italy seismic and deformation network. We are grateful to Stefano Parolai, Gianfranco Vannucci, Mircea Radulian, and Franco Vaccari for their insightful comments and notable feedback that helped to improve the paper.
This research has been supported by the Regione Autonoma Friuli Venezia Giulia and by the Regione Veneto.
This paper was edited by Kirsten Elger and reviewed by Gianfranco Vannucci and Mircea Radulian.
Álvarez-Gómez, J. A.: FMC – Earthquake focal mechanisms data management, cluster and Classification, SoftwareX, 9, 299–307, https://doi.org/10.1016/j.softx.2019.03.008, 2019.
Aki, K. and Richards, P. G.: Quantitative seismology, Freeman, San Francisco, Vol. I and II, 932 pp., 1980.
Anderson, H. and Jackson, J.: Active tectonics of the Adriatic Region, Geophys. J. R. Astron. Soc., 91, 937–983, https://doi.org/10.1111/j.1365-246X.1987.tb01675.x, 1987.
Aoudia, A., Saraò, A., Bukchin, B., and Suhadolc, P.: The 1976 Friuli NE Italy thrust faulting earthquake: a reappraisal 23 years later, Geophys. Res. Lett., 27, 573–576, https://doi.org/10.1029/1999GL011071, 2000.
Bajc, J., Aoudia, A., Saraò, A., and Suhadolc, P.: The 1998 Bovec-Krn (Slovenia) earthquake sequence, Geophys. Res. Lett., 28, 1839–1842, https://doi.org/10.1029/2000GL011973, 2001.
Battaglia, M., Murray, M. H., Serpelloni, E., and Bürgmann, R.: The Adriatic region: an independent microplate within the Africa–Eurasia collision zone, Geophys. Res. Lett., 31, L09605, https://doi.org/10.1029/2004GL019723, 2004.
Benz, H.: Building a National Seismic Monitoring Center: NEIC from 2000 to the Present, Seism. Res. Lett., 88, 457–461, https://doi.org/10.1785/0220170034, 2017.
Bernardis, G., Poli, M. E., Renner, G., Snidarcig, A., and Zanferrari, A.: Le tre sequenze sismiche del 1996 a Claut (Prealpi Carniche), in: Atti GNGTS, 15 Convegno, Roma, 343–348, 1997.
Bragato, P.L., Di Bartolomeo, P., Pesaresi, D., Plasencia Linares, M., and Saraò, A.: Acquiring, archiving, analyzing and exchanging seismic data in real time at the Seismological Research Center of the OGS in Italy, Ann. Geophys. 54, 67–75, https://doi.org/10.4401/ag-4958, 2011.
Bragato P.L., Comelli, P., Saraò, A., Zuliani, D., Moratto, L., Poggi, V., Rossi, G., Scaini, C., Sugan, M., Barnaba, C., Bernardi, P., Bertoni, M., Bressan, G., Compagno, A., Del Negro, E., Di Bartolomeo, P., Fabris, P., Garbin, M., Grossi, M., Magrin, A., Magrin, E., Pesaresi, D., Petrovic, B., Plasencia Linares, M. P., Romanelli, M., Snidarcig, A., Tunini, L., Urban, S., Venturini, E., and Parolai, S.: The OGS- North-Eastern Italy Seismic and Deformation Network: current status and outlook, Seism. Res. Lett., 92, 1704–1716, https://doi.org/10.1785/0220200372, 2021.
Bressan, G.: Modelli di velocitaÌ 1D dell'Italia Nord Orientale, Internal report OGS CRS/5/20/2005, Udine, 18 pp., 2005 (in Italian).
Bressan, G., Bragato, P. L., and Venturini, C.: Stress and strain tensors based on focal mechanisms in the seismotectonic framework of the Friuli–Venezia Giulia region (north-eastern Italy), Bull. Seism. Soc. Am., 93, 1280–1297, https://doi.org/10.1785/0120020058, 2003.
Bressan, G., Kravanja, S., and Franceschina, G.: Source parameters and stress release of seismic sequences occurred in the Friuli-Venezia Giulia region (Northeastern Italy) and in Western Slovenia, Phys. Earth Planet. Int., 160, 192–214, https://doi.org/10.1016/j.pepi.2006.10.005, 2007.
Bressan, G., Gentile, G. F., Perniola, B., and Urban, S.: The 1998 and 2004 Bovec-Krn (Slovenia) seismic sequences: aftershock pattern, focal mechanisms and static stress changes, Geophys. J. Int., 179, 231–253, https://doi.org/10.1111/j.1365-246X.2009.04247.x, 2009.
Bressan, G., Barnaba, C., Bragato, P., Ponton, M., and Restivo, A.: Revised seismotectonic model of NE Italy and W Slovenia based on focal mechanism inversion, J. Seismol., 22, 1563–1578, https://doi.org/10.1007/s10950-018-9785-2, 2018.
Bressan, G., Barnaba, C., Bragato, P. L., Peresan, A., Rossi, G., and Urban, S.: Distretti sismici del Friuli Venezia Giulia, B. Geofis. Teor. Appl., 60, 1–74, 2019.
Cagnetti, V., Pasquale, V., and Polinari, S.: Focal mechanisms of earthquakes in Italy and adjacent regions, CNEN Rt/Amb 76, 4, Roma, 41 pp., 1976.
Centro di Ricerche Sismologiche (CRS): Friuli-Venezia Giulia Seismometric Network Bulletin, available at: http://www.crs.inogs.it/bollettino/RSFVG/RSFVG.en.html, last access: 22 September, 2020.
Clinton, J. F., Hauksson E., and Solanki, K.: An Evaluation of the SCSN Moment Tensor Solutions: Robustness of the Mw Magnitude Scale, Style of Faulting, and Automation of the Method, Bull. Seism. Soc. Am., 96, 1689–1705, https://doi.org/10.1785/0120050241, 2006.
Constantinescu, L., Ruprechtová, L., and Enescu, D.: Mediterranean-Alpine Earthquake Mechanisms and their Seismotectonic Implications, Geophys. J. Int., 10, 347–368, https://doi.org/10.1111/j.1365-246X.1966.tb03063.x, 1966.
Custódio, S., Lima, V., Vales, D., Cesca, S., and Carrilho, F.: Imaging active faulting in a region of distributed deformation from the joint clustering of focal mechanisms and hypocentres: application to the Azores–western Mediterranean region, Tectonophysics 676, 70–89, https://doi.org/10.1016/j.tecto.2016.03.013, 2016.
D'Agostino, N., Cheloni, D., Mantenuto, S., Selvaggi, G., Michelini, A., Zuliani, D.: Strain accumulation in the Southern Alps (NE Italy) and deformation at the northeastern boundary of Adria observed by CGPS measurements., Geophys. Res. Lett., 32, https://doi.org/10.1029/2005GL024266, 2005.
D'Agostino, N., Avallone, A., Cheloni, D., D'Anastasio, E., Mantenuto, S., and Selvaggi, G.: Active tectonics of the Adriatic region from GPS and earthquake slip vectors, J. Geophys. Res., 113, B12413, https://doi.org/10.1029/2008JB005860, 2008.
Danesi, S., Pondrelli, S., Salimbeni, S., Cavaliere, A., Serpelloni, E., Danecek, P., Lovati, S., and Massa, M.: Active deformation and seismicity in the Southern Alps (Italy): The Montello hill as a case study, Tectonophysics, 653, 95–108, https://doi.org/10.1016/j.tecto.2015.03.028, 2015.
Del Ben, A., Finetti, I., Rebez, A., and Slejko, D.: Seismicity and seismotectonics at the Alps-Dinarides contact, Boll. Geof. Teor. Appl., 33, 130–131, 155–175, 1991.
Dreger, D. and Helmberger, D. V.: Determination of source parameters at regional distances with three component sparse network data, J. Geophys. Res., 98, 8107–8125, https://doi.org/10.1029/93JB00023, 1993.
Dreger, D., Uhrhammer, R., Pasyanos, M., Franck, J., and Romanowicz, B.: Regional and Far-Regional Earthquake Locations and Source Parameters Using Sparse Broad Band Networks: A test on the Ridgecrest Sequence, Bull. Seism. Soc. Am., 88, 1353–1362, 1998.
Dreger, D. S.: TDMT_INV: Time Domain Seismic Moment Tensor INVersion, International Handbook of Earthquake and Engineering Seismology, 81B, 1627, https://doi.org/10.1016/S0074-6142(03)80290-5, 2003.
Dziewonski, A. M., Chou, T. A., and Woodhouse, J. H.: Determination of earthquake source parameters from waveform data for studies of global and regional seismicity, J. Geophys. Res., 86, 2825–2852, https://doi.org/10.1029/JB086iB04p02825, 1981.
Dziewonski, A. M. and Woodhouse, J. H.: An experiment in systematic study of global seismicity: centroid-moment tensor solutions for 201 moderate and large earthquakes of 1981, J. Geophys. Res., 88, 3247–3271, https://doi.org/10.1029/JB088iB04p03247, 1983.
EIDA Italia Node: http://eida.ingv.it/it/, last access: 17 May 2021.
Ekström, G., Nettles, M., and Dziewonski, A. M.: The global CMT project 2004–2010: Centroid-moment tensors for 13,017 earthquakes, Phys. Earth Planet. Inter., 200–201, 1–9, https://doi.org/10.1016/j.pepi.2012.04.002, 2012.
Galadini, F., Poli, M. E., and Zanferrari, A.: Seismogenic sources potentially responsible for earthquakes with M ≥ 6 in the eastern Southern Alps (Thiene-Udine sector, NE Italy), Geophys. J. Int., 161, 739–762, https://doi.org/10.1111/j.1365-246X.2005.02571.x, 2005.
Gasperini, P. and Vannucci, G.: FPSPACK: A package of FORTRAN subroutines to manage earthquake focal mechanism data, Comput. Geosci., 29, 893–901, https://doi.org/10.1016/S0098-3004(03)00096-7, 2003.
Gentili, S., Sugan, M., Peruzza, L., and Schorlemmer, D.: Probabilistic completeness assessment of the past 30 years of seismic monitoring in northeastern Italy, Phys. Earth Planet. Inter., 186, 81–96, https://doi.org/10.1016/j.pepi.2011.03.005, 2011.
GEOFON Data centre: GEOFON Moment Tensor Solutions, available at: http://geofon.gfz-potsdam.de/eqinfo/list.php?mode=mt, last access: 3 November 2020.
Gerner, P.: Catalogue of Earthquake Focal Mechanism Solutions for the Pannonian Region, Geophysical Department, Eötvös University, Budapest, 38 pp., 1995.
Gilbert, F.: Excitation of the normal modes of the Earth by earthquakes sources., Geophys. J. Roy. Astr. Soc., 22, 223–226, https://doi.org/10.1111/j.1365-246X.1971.tb03593.x, 1970.
Heidbach, O., Rajabi, M., Cui, X., Fuchs, K., Müller, B., Reinecker, J., Reiter, K., Tingay, M., Wenzel, F., Xie, F., Ziegler, M. O., Zoback, M. L., and Zoback, M. D.: The World Stress Map database release 2016: Crustal stress pattern across scales, Tectonophysics, 744, 484–498, https://doi.org/10.1016/j.tecto.2018.07.007, 2018.
Herak, M., Herak, D., and Markusic, S.: Fault plane solution for earthquakes (1956–1995) in Croatia and neighbouring regions, Geofizika, 12, 43–56, 1995.
International Seismological Centre: Seismological Dataset Repository, https://doi.org/10.31905/6TJZECEY, last access: 12 July 2020.
Ishibe, T., Tsuruoka, H., Satake, K., and Nakatani, M.: A Focal Mechanism Solution Catalog of Earthquakes (M≥2.0) in and around the Japanese Islands for 1985–1998, Bull. Seism. Soc. Am., 104, 1031–1036, https://doi.org/10.1785/0120130278, 2014.
Kagan, Y. Y.: 3-D rotation of double-couple earthquake sources, Geophys. J. Int., 106, 709–716, https://doi.org/10.1111/j.1365-246x.1991.tb06343.x, 1991.
Kapetanidis, V. and Kassaras, I.: Contemporary crustal stress of the Greek region deduced from earthquake focal mechanisms, J. Geodynam., 123, 55–82, https://doi.org/10.1016/j.jog.2018.11.004, 2019.
Kastelic, V., Vrabec, M., Cunningham, D., and Gosar, A.: Neo-Alpine structural evolution and present-day tectonic activity of the eastern Southern Alps: the case of the Ravne Fault, NW Slovenia, J. Struct. Geol., 30, 963–975, 2008.
Kaverina, A. N., Lander, A. V., and Prozorov, A. G.: Global creepex distribution and its relation to earthquake-source geometry and tectonic origin, Geophys. J. Int., 125, 249–265, https://doi.org/10.1111/j.1365-246X.1996.tb06549.x, 1996.
Knopoff, L. and Gilbert, F.: First motions from seismic sources, Bull. Seism. Soc. Am., 50, 117–134, 1960.
Kubo, A., Fukuyama, E., and Nonomura, K.: NIED seismic moment tensor catalogue for regional earthquakes around Japan: quality test and application, Tectonophysics, 356, 23–48, https://doi.org/10.1016/S0040-1951(02)00375-X , 2002.
Lee, W. H. K. and Lahr, J. C.: Hypo 71 (revised): a computer program for determining hypocentre, magnitude and firs motion pattern of local earthquakes, USGS Open File Report 75-311, Menlo Park, 113 pp., 1975.
Lentas, K., Di Giacomo, D., Harris, J., and Storchak, D. A.: The ISC Bulletin as a comprehensive source of earthquake source mechanisms, Earth Syst. Sci. Data, 11, 565–578, https://doi.org/10.5194/essd-11-565-2019, 2019.
Locati, M., Camassi, R., Rovida, A., Ercolani, E., Bernardini, F., Castelli, V., Caracciolo, C. H., Tertulliani, A., Rossi, A., Azzaro, R., D'Amico, S., Conte, S., and Rocchetti, E.: Database Macrosismico Italiano (DBMI15), Istituto Nazionale di Geofisica e Vulcanologia (INGV), Roma, Italia, https://doi.org/10.6092/INGV.IT-DBMI15, 2016.
McKenzie, D.: Active tectonics of the Mediterranean Region, Geophys. J. R. Astr. Soc., 30, 109–185, https://doi.org/10.1111/j.1365-246X.1972.tb02351.x, 1972.
Meletti, C., Marzocchi, W., D'Amico, V., Lanzano, G., Luzi, L., Martinelli, F., Pace, B., Rovida, A., Taroni, M., Visini, F. and the MPS19 Working Group: The new Italian Seismic Hazard Model, Ann. Geophys., 64, 1–29, https://doi.org/10.4401/ag-8579, 2021
Nakamura, W., Uchida, N., and Matsuzawa, T.: Spatial distribution of the faulting types of small earthquakes around the 2011 Tohokuoki earthquake: A comprehensive search using template events, J. Geophys. Res.-Sol. Ea., 121, 2591–2607, https://doi.org/10.1002/2015JB012584, 2016.
OGS (Istituto Nazionale Di Oceanografia E Di Geofisica Sperimentale): North-East Italy Seismic Network. International Federation of Digital Seismograph Networks, https://doi.org/10.7914/SN/OX, 2016.
Peruzza, L., Garbin, M., Snidarcig. A., Sugan, M., Urban, S., Renner, G., and Romano, M. A.: Quarry blasts, underwater explosions and other dubious seismic events in NE Italy from 1977 till 2013, Boll. Geof. Teor. Appl., 56, 437–459, https://doi.org/10.4430/bgta0159, 2015.
Peruzza L., Iliceto V., and Slejko D.: Some seismotectonic aspects of the Alpago-Cansiglio area (N.E. Italy), Boll. Geof. Teor. Appl., 31, 63–75, 1989.
Poli, M. E. and Renner, G.: Normal focal mechanism in the Julian Alps and Prealps: seismotectonic implications for the Italian-Slovenian Border region, Boll. Geof. Teor. Appl., 45, 51–69, 2004.
Poli, M. E., Peruzza, L., Rebez, A., Renner, G., Slejko, D., and Zanferrari, A.: New seismotectonic evidence from the analysis of the 1976–1977 and 1977–1999 seismicity in Friuli (NE Italy), Boll. Geof. Teor. Appl., 43, 53–78, 2002.
Pondrelli, S., Ekström, G., and Morelli, A.: Seismotectonic re-evaluation of the 1976 Friuli, Italy, seismic sequence, J. Seism., 5, 73–83, https://doi.org/10.1023/A:1009822018837, 2001.
Pondrelli, S. and Salimbeni, S.: Regional moment tensor review: an example from the European–Mediterranean Region, in Encyclopedia of Earthquake Engineering, 1–15, Springer Berlin Heidelberg, https://doi.org/10.1007/978-3-642-36197-5_301-1, 2015.
Priolo, E., Barnaba, C., Bernardi, P., Bernardis, G., Bragato, P.L., Bressan, G., Candido, M., Cazzador, E., Di Bartolomeo, P., DuriÌ, G., Gentili, S., Govoni, A., Klinc, P., Kravanja, S., Laurenzano, G., Lovisa, L., Marotta, P., Michelini, A., Ponton F., Restivo, A., Romanelli, A., Snidarcig, A., Urban, S., Vuan, A., and Zuliani, D.: Seismic monitoring in northeastern Italy: A ten-year experience, Seismol. Res. Lett., 76, 446–454, https://doi.org/10.1785/gssrl.76.4.446, 2005.
Radulian, M., Popescu, E., Bala, A., and Utale, A.: Catalog of fault plane solutions for the earthquakes occurred on the Romanian territory, Rom. J. Phys., 47, 663–686, 2002.
Reasenberg, P. and Oppenheimer, D.: FPFIT, FPPLOT and FPPAGE: Fortran computer programs for calculating and displaying earthquake fault-plane solutions, Open-File Rep., 85-739, USGS, Menlo Park, 109 pp., 1985.
Restivo, A., Bressan, G., and Sugan, M.: Stress and strain patterns in the Venetian Prealps (north-eastern Italy) based on focal-mechanism solutions, Boll. Geof. Teor. Appl., 57, 13–30, https://doi.org/10.4430/bgta0166, 2016.
Riggio, A. and Russi, M.: Procedura di analisi ed elaborazione dei dati registrati da reti sismometriche locali, in: FinalitaÌ ed Esperienze della Rete Sismometrica del Friuli-Venezia Giulia, Reg. Aut. Friuli-Venezia Giulia, Trieste, Italy, 53–74, 1984.
Romano, M. A., Peruzza, L., Garbin, M., Priolo, E., and Picotti, V.: Microseismic portrait of the Montello thrust (Southeastern Alps, Italy) from a dense, high-quality seismic network, Seismol. Res. Lett., 90, 1502–1517, https://doi.org/10.1785/0220180387, 2019.
Rovida, A., Locati, M., Camassi, R., Lolli, B., and Gasperini, P.: The Italian earthquake catalogue CPTI15, Bull. Earth. Eng., 18, 2953–2984, https://doi.org/10.1007/s10518-020-00818-y, 2020.
Rovida, A., Locati, M., Camassi, R., Lolli, B., Gasperini, P., and Antonucci, A.: Catalogo Parametrico dei Terremoti Italiani (CPTI15), versione 3.0, Istituto Nazionale di Geofisica e Vulcanologia (INGV), https://doi.org/10.13127/CPTI/CPTI15.3, 2021.
Saikia, C. K.: Modified frequency-wavenumber algorithm for regional seismograms using Filon's Quadrature- Modeling of Lg waves in eastern North America, Geophys. J. Int., 118, 142–158, https://doi.org/10.1111/j.1365-246X.1994.tb04680.x , 1984.
Sandron, D., Rebez, A., and Slejko, D.: Calibration of the duration magnitude for the north-eastern Italy Seismic Network (OX) on the basis of the revised local magnitudes of the Trieste Station, Boll. Geof. Teor. Appl., 59, 249–266, https://doi.org/10.4430/bgta0237, 2018.
Saraò, A.: Seismic moment tensor determination at CRS: feasibility study, Open Report, OGS 2007/60-CRS/16, 43 pp., 2007.
Saraò, A.: Online catalogue of moment tensor solutions of earthquakes occurred in NE Italy and its surroundings in the period 2014–2016, available at: http://bit.ly/2jlxfvv (last access: 20 October 2020), 2016.
Saraò, A.: Seismic moment tensor solutions of Mw>3.4 earthquakes occurred between 2002 and 2018 in the Southeastern Alps, Zenodo, https://doi.org/10.5281/zenodo.4298707, 2020.
Saraò, A., Sugan, M., Bressan, G., Renner, G., and Restivo, A.: Focal mechanisms of the Southeastern Alps and surroundings (Version 1.1) [Data set], Zenodo, https://doi.org/10.5281/zenodo.4660412, 2021.
Scognamiglio, L., Tinti, E., and Quintiliani, M.: Time Domain Moment Tensor (TDMT) [Data set], Istituto Nazionale di Geofisica e Vulcanologia (INGV), https://doi.org/10.13127/TDMT, 2006.
Scognamiglio, E., Tinti, E., and Michelini, A.: Real Time Determination of seismic moment tensor for the Italian Region, Bull. Seism. Soc. Am., 99, 2223–2242, https://doi.org/10.1785/0120080104, 2009.
Serpelloni, E., Anzidei, M., Baldi, P., Casula, G., and Galvani, A.: Crustal velocity and strain-rate fields in Italy and surrounding regions: new results from the analysis of permanent and non-permanent GPS networks, Geophys. J. Int., 161, 861–880, https://doi.org/10.1111/j.1365-246X.2005.02618.x, 2005.
Shearer, P. M.: Evidence from a cluster of small earthquakes for a fault at 18 km depth beneath Oak Ridge, southern California, Bull. Seismol. Soc. Am., 88, 1327–1336, 1998.
Sirovich, L. and Pettenati, F.: Source inversion of intensity patterns of earthquakes: a destructive shock in 1936 in northeast Italy, J. Geophys. Res., 109, B10309, https://doi.org/10.1029/2003JB002919, 2004.
Slejko, D.: What science remains of the 1976 Friuli earthquake?, Boll. Geofis. Theor. Appl., 530, 59, 327–350, https://doi.org/10.4430/bgta0224, 2018.
Slejko, D., Carulli, G. B., Nicolich, R., Rebez, A., Zanferrari, A., Cavallin, A., Doglioni, C., Carraro, F., Castaldini, D., Iliceto, V., Semenza, E., and Zanolla, C.: Seismotectonics of the Eastern Southern-Alps: a review, Boll. Geof. Teor. Appl., 31, 109–136, 1989.
Slejko, D., Peruzza, L., and Rebez, A.: Seismic hazard maps of Italy, Ann. Geophys., 41, 183–214, https://doi.org/10.4401/ag-4327, 1998.
Slejko, D., Neri, G., Orozova, I., Renner, G., and Wyss, M.: Stress field in Friuli (NE Italy) from fault plane solutions of activity following the 1976 main shock, Bull. Seism. Soc. Am., 89, 1037–1052, 1999.
Sugan, M. and Peruzza, L.: Distretti sismici del Veneto, Boll. Geof. Teor. Appl., 52, 3–90, https://doi.org/10.4430/bgta0057, 2011.
Sugan, M., Renner, G., Bressan, G., Restivo, A., and Saraò A.: First motion data and focal mechanism solutions of 108 earthquakes occurred between 1928 and 2019 in the Southeastern Alps [Data set], Zenodo, https://doi.org/10.5281/zenodo.4284929, 2020.
Udías, A., Buforn, E., and Ruiz De Gauna, J.: Catalogue of focal mechanisms of European earthquakes, Department of Geophysics, Universidad Complutense, Madrid, 274 pp., 1989.
Viganò, A., Bressan, G., Ranalli, G., and Martin, S.: Focal mechanism inversion in the Giudicarie–Lessini seismotectonic region (Southern Alps, Italy): Insights on tectonic stress and strain, Tectonophysics, 460, 106–115, https://doi.org/10.1016/j.tecto.2008.07.008, 2008.
Viganò, A., Scafidi, D., Ranalli, G., Martin, S., Della Vedova, B., and Spallarossa, D.: Earthquake relocations, crustal rheology, and active deformation in the central–eastern Alps (N Italy), Tectonophysics, 661, 81–98, https://doi.org/10.1016/j.tecto.2015.08.017, 2015.
Vannucci, G. and Gasperini, P.: The new release of the database of Earthquake Mechanisms of the Mediterranean Area (EMMA Version 2), Ann. Geophys., 47, 307–334, https://doi.org/10.4401/ag-3277, 2004.
Wessel, P., Luis, J. F., Uieda, L., Scharroo, R., Wobbe, F., Smith, W. H. F., and Tian, D.: The Generic Mapping Tools version 6, Geochem. Geophy. Geosy., 20, 5556–5564, https://doi.org/10.1029/2019GC008515, 2019.
Whitcomb, J. H.: Part I. A study of the velocity structure of the Earth by the use of core phases. Part II. The 1971 San Fernando earthquake series, focal mechanisms and tectonics, PhD Thesis, California Institute of Technology, Pasadena, 1973.
Zoback, M. L.: First- and second-order patterns of stress in the lithosphere: the world stress map project, J. Geophys. Res., 97, 11703–11728, https://doi.org/10.1029/92JB00132, 1992.
Zuliani, D., Fabris, P., and Rossi, G.: FReDNet: Evolution of a Permanent GNSS Receiver System, in: New Advanced GNSS and 3D Spatial Techniques, edited by: Cefalo, R., Zieliński, J., and Barbarella, M., Lecture Notes in Geoinformation and Cartography, Springer, Cham, 123–137, https://doi.org/10.1007/978-3-319-56218-6_10, 2018.