Atmospheric data set from the Geodetic Observatory Wettzell during the CONT-17 VLBI campaign

Continuous very long baseline interferometry (VLBI) observations are designed to obtain highly accurate data for detailed studies of high-frequency Earth rotation variations, reference frame stability, and daily to sub-daily site motions. During the CONT-17 campaign that covered a time span of 15 days between 28 November and 12 December 2017, a comprehensive data set of atmospheric observations was acquired at the Geodetic Observatory Wettzell, where three radio telescopes contributed to three different networks which have been established for this campaign. These data were supplemented by weather model data. The data set is made available to all interested users in order to provide an optimal database for the analysis and interpretation of the CONT-17 VLBI data. In addition, it is an outstanding data set for the validation and comparison of tropospheric parameters resulting from different space techniques with regard to the establishment of a common atmosphere at co-location sites.

The regularly recorded atmospheric parameters comprise many meteorological quantities (pressure, temperature, humidity, wind, radiation, and precipitation) taken from the local weather station close to the surface, solar radiation intensity, temperatures up to 1000 m above the surface from a temperature profiler, total vapor and liquid water content from a water vapor radiometer, and cloud coverage and cloud temperatures from a nubiscope. Additionally, vertical profiles of pressure, temperature, and humidity from radiosonde balloons and from numerical weather models were used for comparison and validation.

The graphical representation and comparison show a good correlation in general but also some disagreements in certain weather situations. While the accuracy and the temporal and spatial resolution of the individual data sets are very different, the data as a whole characterize the atmospheric conditions around Wettzell during the CONT-17 campaign comprehensively and represent a sound basis for further investigations (https://doi.org/10.1594/PANGAEA.895518; Klügel et al., 2018).

1 Introduction

1.1 Geodetic VLBI observations and CONT continuous measurement campaigns

The International VLBI (Very Long Baseline Interferometry) Service for Geodesy and Astrometry (IVS) coordinates geodetic VLBI observing programs (Nothnagel et al., 2017). VLBI is important since it is the only geodetic technique capable of deriving the full set of Earth orientation parameters. The IVS has organized special measurement campaigns called “CONT” approximately every 3 years since 2002. These particularly intensive sessions cover 2 weeks of continuous network observations and must be distinguished from the routine observation program consisting of individual 24 and 1 h sessions. The main goal of CONT is to test the accuracy of the VLBI estimates of the Earth orientation parameters and to investigate possible network biases (Behrend et al., 2017). The CONT17 campaign started on 28 November 2017, with observations being carried out in three different networks (Behrend, 2017).

Figure 1 The Geodetic Observatory Wettzell, with atmospheric sensors highlighted in blue.

1.2 The Geodetic Observatory Wettzell and the purpose of atmospheric observations

The Geodetic Observatory Wettzell (GOW) features two SLR (Satellite Laser Ranging) telescopes, several GNSS (Global Navigation Satellite System) reference stations, and a DORIS (Doppler Orbitography and Ranging Integrated by Satellite) beacon, as well as three VLBI telescopes (Schüler et al., 2015). All three radio telescopes participated in CONT17, each of them in one of the three different networks. VLBI, GNSS, and DORIS all operate in the microwave frequency domain. In this case, the atmosphere is a major complicating factor reducing the accuracy (Petit and Luzum, 2010). Consequently, the set of atmosphere sensors at the Geodetic Observatory Wettzell has been substantially enhanced in recent years to provide means to better deal with this problem. The propagation delays induced by the ionosphere can be compensated for with the help of measurements taken at at least two different frequencies.

However, the troposphere (and to a lesser extent also the stratosphere) remains a problem. The microwave signals are delayed when passing through these layers, and these effects are nondispersive; i.e., they are virtually identical at the various frequencies in use. As a consequence, pre-elimination of these propagation errors is not possible. One method to quantify tropospheric errors is to use models. Another one is to introduce tropospheric unknowns as nuisance parameters into the observation equations and to estimate these effects together with the set of target parameters. In practice, a combination of both approaches is usually accomplished. In any case, real measurements of the state of the atmosphere are very valuable to aid in tropospheric delay modeling and to interpret the results and residuals. This is the motivation to compile the atmosphere measurements collected during the CONT17 campaign, forming a comprehensive data set to understand the atmosphere over the Geodetic Observatory Wettzell, to aid VLBI analysis and to support studies dealing with the comparison of troposphere delays of microwaves derived from different techniques (e.g., Teke et al., 2013; Lu et al., 2015).

Table 1 Sensors of the local weather station. Except for the pressure sensor, the height is given in meters above the surface. Specified accuracies are manufacturer information.

2 Study area and instrumentation

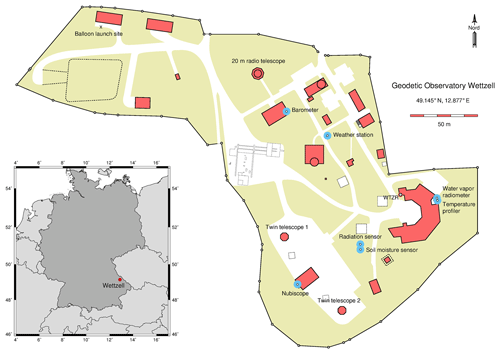
The Geodetic Observatory Wettzell is located in eastern Bavaria on a flat mountain ridge about 600 m a.s.l., that is, above standard elevation zero (NHN) of the German height system (DHHN). The topography in the surroundings ranges from valley floors (∼400 m a.s.l.) to mountain ridges (∼1000 m a.s.l.). Land coverage is characterized by grassland and forest. A plan view of the observatory with the instrument locations is depicted in Fig. 1. The following sections give a description of the instruments deployed and the quantities measured.

2.1 Local weather station

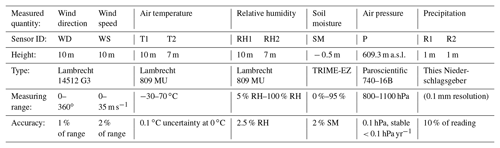
The temperature, humidity, and wind sensors of the local weather station are mounted on a concrete tower at 7 and 10 m height above the surface (Table 1). The air pressure sensor is inside the 20 m radio telescope control building, and the rain gauges are mounted on a platform as shown in Fig. 1. Data are continuously acquired, and averages are recorded once per minute. For wind direction and wind speed, minimum and maximum values measured within 1 min are also stored, indicated by “<” and “>”. The heated rain gauges measure snow as well and record the sum over 1 min.

Table 2 Retrieval coefficients used (in centimeters).

Table 3 Structure of the grid file “we_iconeu_4deg.grd”.

2.2 Radiation sensor

As an addition to the meteorological station, global radiation is measured using a pyranometer, Thies CM 11. At the same place a net radiometer (Kipp & Zonen NR Lite) measures the difference between radiation from above, i.e., the sun and the sky, and from below, i.e., the soil surface. Both sensors are installed 1.5 m above the grass surface. The sampling rate is 10 min.

2.3 Temperature profiler

A quasi-continuous record of temperatures in the atmosphere up to 1000 m height is realized by a radio wave radiometer, MTP-5, from R.P.O. Attex. The microwave receiver measures the blackbody thermal radiation of the atmosphere at a frequency of 56.6 GHz. The intensity of the radiation is a function of the temperature. By scanning the atmosphere at different elevation angles, the operating software computes temperatures at different heights in 50 m steps up to 1000 m, under the assumption of a horizontal temperature layering. The basic principle and some field examples are described in Peña et al. (2013).

The temperature profiler is installed on a tower at 619 m a.s.l. and 10 m above ground. A complete profile is recorded every 5 min. The measurement uncertainty increases with height and is specified to be 0.2 to 1.2 ^∘C, depending on the profile type and height.

2.4 Water vapor radiometer

On the same tower as the temperature profiler, a water vapor radiometer, Radiometrics WVR-1100, is installed. It is a microwave receiver measuring the intensity of atmospheric radiation at 23.8 and 31.4 GHz. The water vapor dominates the 23.8 GHz observations, whereas the cloud liquid in the atmosphere dominates the power in the 31.4 GHz channel. This allows the simultaneous determination of integrated water vapor and liquid water along the line of sight. From the measured brightness temperatures at both frequencies, Tb₂₃ and Tb₃₁, the frequency-dependent atmospheric opacities τ₂₃ and τ₃₁ are calculated. The water vapor and liquid water content and the path delay are obtained using the following relationships:

$$\begin{array}{}\text{(1)}& {\displaystyle }& {\displaystyle }\mathrm{Vap}=c{\mathrm{0}}_{\mathrm{vap}}+c{\mathrm{1}}_{\mathrm{vap}}\cdot {\mathit{\tau }}_{\mathrm{32}}+c{\mathrm{2}}_{\mathrm{vap}}\cdot {\mathit{\tau }}_{\mathrm{31}}\text{(2)}& {\displaystyle }& {\displaystyle }\mathrm{Liq}=c{\mathrm{0}}_{\mathrm{liq}}+c{\mathrm{1}}_{\mathrm{liq}}\cdot {\mathit{\tau }}_{\mathrm{32}}+c{\mathrm{2}}_{\mathrm{liq}}\cdot {\mathit{\tau }}_{\mathrm{31}}\text{(3)}& {\displaystyle }& {\displaystyle }\mathrm{Del}=c{\mathrm{0}}_{\mathrm{del}}+c{\mathrm{1}}_{\mathrm{del}}\cdot {\mathit{\tau }}_{\mathrm{32}}+c{\mathrm{2}}_{\mathrm{del}}\cdot {\mathit{\tau }}_{\mathrm{31}}.\end{array}$$

The retrieval coefficients c0, c1, and c2 are site-dependent and have to be determined from a history of radiosonde observations from a representative site. The retrieval coefficients used in this work are valid for Munich and displayed in Table 2. The blackbody temperature, Tk_BB, as given in col. 4 of the data file, is only used to establish the temperature coefficient of the instrument gain. A description of the determination of atmospheric water vapor using microwave radiometry is given, e.g., in Elgered et al. (1982).

The instrument performs about one measurement per minute in one particular direction. In azimuth steps of 30^∘, elevation scans between 20^∘ and 160^∘ are carried out; i.e., the scan passes over the zenith direction. For a complete scan of the entire sky, it takes about 90 min. In order to obtain the zenith delay only, all lines with 90^∘ elevation have to be extracted from the data files. This results in 198 zenith data points per day.

The accuracy of the brightness temperature measurement is specified with 0.5 K. The accuracy of the resulting water vapor and liquid water contents and phase delays strongly depends on the instrument calibration, i.e., the retrieval coefficients used.

2.5 Cloud detector

The cloud detector or nubiscope measures the thermal radiation of the sky in one particular direction. Since clouds absorb radiation from the sun and reflected infrared radiation from the ground, the temperature of the cloud base is significantly higher than the clear sky. By scanning the entire sky, a map of the cloud coverage can be generated. As low clouds generally yield higher temperatures than high clouds, additional information regarding the height of the clouds is obtained. Taking into account the horizon effect, that is, the temperature increase from zenith to horizon, the processing software determines the fraction of low-, medium- and high-level clouds, the coverage, temperature, and height of the main cloud base, and the temperature and height of the lowest clouds. Further information is given on the manufacturer's website (Sattler, no year).

The cloud detector is installed on an observation platform on the roof of the Twin Telescope operation building at 625 m a.s.l. and 9 m above the surface. The recorded heights of the cloud base refer to the instrument height. A complete scan of the sky is done once every 10 min.

2.6 Radiosondes

Every day during the CONT17 experiment, radiosonde balloons were launched at 8:00 and 14:00 UTC at the launch site depicted in Fig. 1. We used Graw DFM-09 radiosondes and helium-filled Totex 350 balloons with 300 g buoyancy. The transmission rate is one data set per second. The radiosondes are equipped with a GPS receiver, permitting an absolute localization with an accuracy of 5 m in horizontal and 10 m in vertical position. The tracking allows precise measurements of wind speed and wind direction at different heights, with an accuracy of 0.2 m s⁻¹, and ascent and descent rates. The air pressure is computed from the surface pressure at the station, the geopotential height, and the temperature, with an accuracy of 0.3 hPa. The accuracy of the temperature and relative humidity sensors is specified with 0.2 ^∘C and 4 %, respectively. The relative humidity h_rel can be expressed as water vapor pressure e using

$$\begin{array}{}\text{(4)}& e=e_s\cdot {\displaystyle \frac{h_{\mathrm{rel}}}{\mathrm{100}}}\end{array}$$

and the Magnus formula according to Sonntag (1990) for the saturation vapor pressure for water in hPa

$$\begin{array}{}\text{(5)}& e_s=\mathrm{6.112}\cdot e^{\frac{\mathrm{17.62}\cdot T}{\mathrm{243.12}+T}},\end{array}$$

with the temperature T in ^∘C.

Each radiosonde launch yields two files, a profile data file with measured and derived meteorological quantities and a position data file from the GPS receiver. Both files were merged to one file using time interpolation when necessary (see Table 5).

Table 4 Parameters from linear regression between temperatures from radiosonde ascents (x) and temperature profiler (y): slope b, y axis offset a, rms fit error, and rms of temperature differences.

3 Weather models

3.1 DWD ICON-EU model

For the time span covering the CONT17 campaign, a data set was extracted from the ICON-EU model from the German Weather Service (Deutscher Wetterdienst, DWD) containing pressure, temperature, and humidity data at different height levels. The ICON-EU model is a refined domain (local nest) of the global ICON (ICOsahedral Nonhydrostatic) model, whose grid is made up by a set of nearly equal spherical triangles spanning the entire Earth (Reinert et al., 2018). The ICON-EU nest is refined by dividing each triangle into four subtriangles, resulting in a grid spacing of ∼6.5 km. It includes 60 height levels up to 22.5 km. The physical parameters at the top of the model are controlled by the global model reaching a height of 75 km.

The extracted subset covers a radius of 4^∘ (∼445 km) around the GOW. The structure of the grid file “we_iconeu_4deg.grd” is given in Table 3, where each line represents one of the 13 941 grid points. The data files are named “we_iconeu_4deg_yyyymmddhh.xxx”, where yyyy denotes the year, mm the month, dd the day, hh the hour, and xxx the physical quantity.

• pre: air pressure (hPa)

• tem: temperature (K)

• hum: water vapor pressure (hPa)

As the model is built up of 60 layers, the temperature and humidity files comprise 60 columns and the pressure file 61 columns, since temperature and humidity are given within the layers and the pressure at the layer boundaries. Each line represents the same grid point as given in the grid file.

The model data represent the atmospheric analysis fields at the beginning of each forecast run and are computed every 3 h using assimilated observed data.

Figure 2 Traces of radiosonde balloons, with maximum heights indicated by red stars.

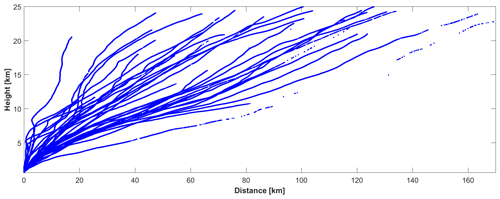
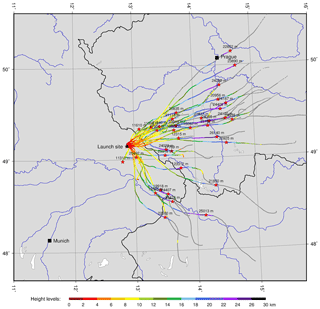
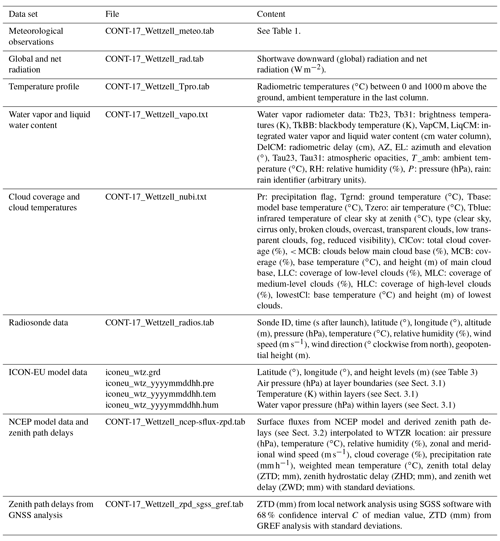
Figure 3 Height–distance plot of all balloon ascents. The height axis is exaggerated by a factor of 2.

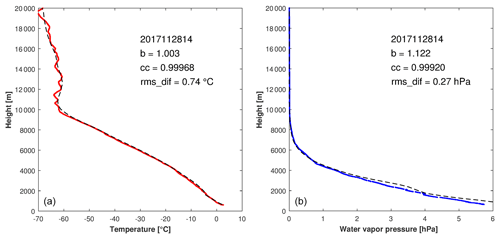
Figure 4 Height profiles of temperature (a) and water vapor content (b) of one particular radiosonde ascent as compared to the weather model profile at the launch location (dotted line). The correlation parameters between both series (b: slope of the best fit line, cc: correlation coefficient, rms_dif: rms of differences) are indicated.

3.2 NCEP model

As a comparative data set, both zenith hydrostatic and wet delays (ZHDs and ZWDs) from the NCEP (National Center for Environmental Prediction) global numerical weather model are provided. This data set is derived from GDAS (Global Data Assimilation System) and GSF (Global Forecasting System) weather fields. The derivation of these tropospheric path delay data requires some explanation because only one dimensional output file from the GDAS numerical weather model (so-called “surfaces fluxes”) was used. From our experience, zenith total delays are expected to reveal a standard deviation approaching 1 cm for the region of Wettzell. This is slightly less accurate than the estimation of tropospheric delays using GNSS permanent stations (see Fig. 9) but still useful for a number of applications.

The original weather model output data can be found on the ftp server at http://ftp.ncep.noaa.gov/ (last access: 22 February 2019) in the directory “/data/nccf/com/gfs/prod”, all available in standard grib2 format. Note that this is a rolling real-time archive. Regions of interest are routinely extracted at our observatory and converted into a tailored format, addressing the specific needs of space geodesy. Analysis fields are used whenever possible (every 6 h) with one 3 h prediction in between.

Figure 5 Temperature profiler (T-profiler) time series at particular heights compared to the temperature record of weather station and radiosonde data at equivalent heights (dots).

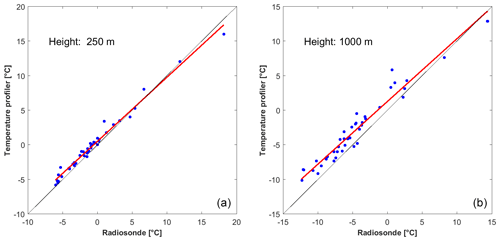
Figure 6 Linear regression between temperatures from radiosonde ascents and contemporaneous profiler records at two particular heights. For regression parameters, see Table 4.

The necessary information is horizontally interpolated and vertically reduced to the central GNSS station WTZR at the observatory. The horizontal interpolation approach is depicted in Schüler (2001, p. 197ff) using the four nearest neighbors, but as a modification, bilinear functions of type $a_{\mathrm{0}}+a_{\mathrm{1}}\cdot \mathit{\varphi }+a_{\mathrm{2}}\cdot \mathit{\lambda }+a_{\mathrm{3}}\cdot \mathit{\varphi }\cdot \mathit{\lambda }$ are employed for interpolation of the surface flux data, where $a_{\mathrm{0},\mathrm{\dots },\mathrm{3}}$ are the interpolation coefficients determined from the four nearest neighbors, ϕ is the latitude of the interpolation site, and λ is its longitude. Vertical reduction to the target height is important. The TropGrid2 model (Schüler, 2014) is used for this purpose. TropGrid2 is a global gridded 1^∘ × 1^∘ model containing reduction coefficients for all quantities needed. The coefficients of these reduction functions were derived using 9 years of numerical weather model data.

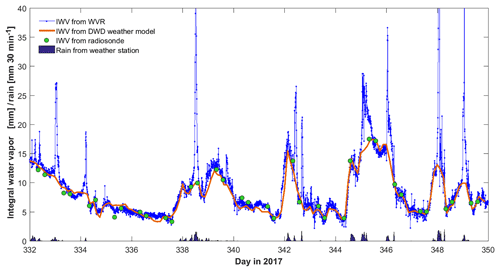
Figure 7 Integrated water vapor (IWV) content as measured by the water vapor radiometer (WVR) compared to IWV values derived from weather model and radiosonde data. WVR spikes coincide with periods of rain.

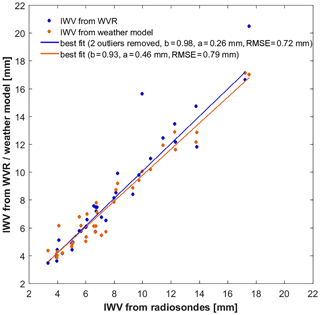
Figure 8 Linear regression between integrated water vapor (IWV) content derived from radiosonde data and that from water vapor radiometer (WVR) and weather model data. The two outliers were removed in the regression.

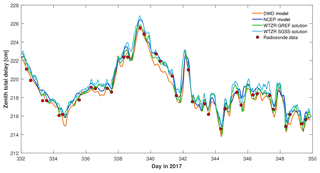
Figure 9 Zenith total delays (ZTDs) derived from numerical weather models, GNSS solutions, and radiosonde data.

The determination of ZHD (zenith hydrostatic delay) from GDAS and GSF surface fields is straightforward: surface pressure is horizontally interpolated and vertically reduced and then converted into ZHD using the Saastamoinen model (Saastamoinen, 1972):

$$\begin{array}{}\text{(6)}& \mathrm{ZHD}={\displaystyle \frac{\mathrm{0.0022767}\cdot p}{\mathrm{1}-\mathrm{0.00266}\cdot \cos \left(\mathrm{2}\mathit{\varphi }\right)-\mathrm{0.00028}\cdot h}},\end{array}$$

with the pressure p (hPa), the ellipsoidal height h (km), and the geographic latitude ϕ of the station. The derivation of ZWD (zenith wet delay) requires more effort, but GDAS/GSF surface fluxes are a very attractive resource since these weather fields already contain the total column atmospheric water vapor (IWV, integrated water vapor). These values are converted into ZWD with knowledge of the weighted mean temperature of the atmosphere T_M (see Schüler, 2001, p. 184ff). T_M itself is substituted in the standard product by a surface temperature conversion function available on the TropGrid2 data grid. After conversion, ZWD is vertically reduced and horizontally interpolated to the target height.

4 Data availability

All data sets are available at https://doi.org/10.1594/PANGAEA.895518 (Klügel et al., 2018). In all time series, the first column represents UTC date and time, with the format yyyy-mm-ddThh:mm:ss. The columns are separated by tabs (\t) in all files with the exception of the ICON-EU model data for which blanks (\s) are used. The ICON-EU model data are stored in a compressed tar archive; all other files are available as ASCII text files. The file description is given in Table 5.

5 Data representation and results

The data from the radiosonde balloon ascents give a direct temperature and humidity profile through the troposphere and are thus a proper tool to validate the weather model and to calibrate radiation-based sensors like the water vapor radiometer or the temperature profiler. The radiosonde ascents between 28 November and 15 December reached heights between 5.6 km (14 December 2017 08:00 launch) and 25.8 km (13 December 2017 08:00 launch) with an average at 19 km. The average ascent rates were between 4 and 6 m s⁻¹ in most cases. The maximum covered horizontal distance to the burst point was 170 km towards northeast (Fig. 2). The horizontal drift is 2–8 km per kilometer of height in most cases (Fig. 3). This means that the tropospheric data up to 10 km height are representative of a region 20–80 km mainly to the east of the launch site.

Table 5 Description of the data set.

The radiosonde temperature profiles coincide well with those of the weather model (see example in Fig. 4a). Some small-scale perturbations in the radiosonde data are not present in the model; however, the trend is always in accord. The linear regression between the weather model temperatures and those from the radiosondes interpolated to the model layer heights yields linear trends (b) and Pearson correlation coefficient (cc) values very close to 1, underlining the high consistency of the model. The only misfit occurred at the 1 December 2017 08:00 launch. In this particular case the measured height seemed to be corrupted. Ignoring this launch, a mean correlation coefficient of 0.9992 is obtained.

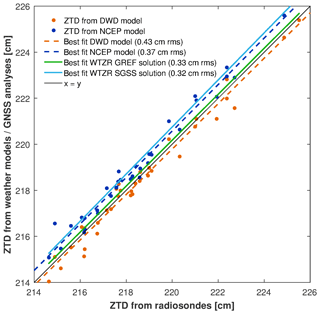
Figure 10 Linear regression between zenith total delays (ZTDs) derived from radiosonde data and those derived from numerical weather models and GNSS solutions.

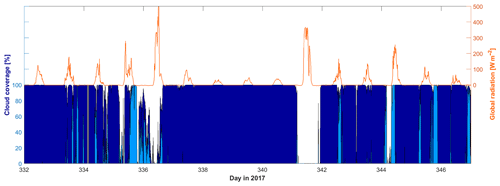
Figure 11 Total cloud coverage (dark blue) and portion of medium- plus high-level clouds (light blue) in comparison with the global radiation as measured by the pyranometer.

A slightly worse agreement exists between the water vapor contents of the weather model and those derived from the radiosonde measurements. As for temperature, small-scale perturbations are not represented in the weather model. The general trend is similar; however, the model tends towards higher water vapor contents, which is also expressed in the greater slope of the trend line (Fig. 4 right), which are between 1.0 and 1.2 in most cases. The mean correlation coefficient is 0.9898.

A graphical representation of measured pressure, temperature, and water vapor profiles from all radiosonde ascents in comparison to model data is given in the Supplement of the data repository.

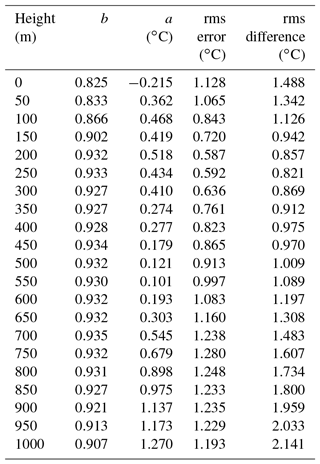
The radiosonde data can also be used to validate the temperature profiler. Figure 5 shows the traces of the temperature profiler at six different height levels compared to temperatures measured by the radiosondes at the equivalent height. While a good coincidence is given at heights up to 400 m, the higher levels yield systematically higher temperatures using the profiler. The root mean square (rms) of the temperature differences at a particular height increases from 0.82 at 250 m up to 2.14 at 1000 m (Table 4). This behavior is underlined by the parameters of linear regression between both temperatures. The slope of the regression line (b) is always lower than 1, and the y axis offset (a) increases with height. This indicates that the profiler particularly underestimates the lower temperatures at higher levels. Examples of one better and one worse agreement are given in Fig. 6.

One quantity inferred from the measured sky brightness temperatures by the water vapor radiometer is the integrated water vapor content given in height of the equivalent water column. In order to compare this quantity with weather model and radiosonde data, the water vapor pressure e was converted to specific humidity s using the following relationship (e.g., Simmer, 2006):

$$\begin{array}{}\text{(7)}& s={\displaystyle \frac{\mathrm{0.622}\cdot e}{p-\mathrm{0.378}\cdot e}}.\end{array}$$

The dimensionless parameter s is then integrated level by level over the vertical column of the weather model or radiosonde profile. The resulting water height equivalents are compared with those measured by the WVR in Fig 7. The general agreement is good; however, the WVR produces outliers during periods of rain. This known issue is a consequence of rain droplets resting on the radiometer window and falsifying the results, even after the rainfall stopped. This can clearly be seen in Fig. 7 at the beginning of day 345, when after the end of the rain the WVR still yields anomalous high IWV values. The linear regression with radiosonde data shows a fairly good agreement of both the WVR and the weather model when the outliers are removed (Fig. 8). If not, the WVR tends to slightly overestimate the water vapor content. The two outliers in the WVR data are due to raindrops after rainfall on day 338 (afternoon) and day 345 (morning) and removed in the computation of the regression parameters. It should be noted, however, that the retrieval coefficients used here are valid for Munich, which is 200 km away, since a reliable determination of retrieval coefficients requires continuous radiosonde data over at least 1 year, which were not available at our site. Thus the total accuracy of the estimated water vapor and liquid water content, for which uncertainties from the brightness temperature measurement and retrieval coefficients add up, cannot be specified. In addition, the vertical profile of the radiosonde is not necessarily representative of the launch site due to the horizontal drift of the balloon (see Fig. 3).

The water content is an important quantity for the estimation of the zenith total delay (ZTD), which is the delay radio waves undergo during their propagation through the atmosphere. The zenith delays can be mapped to the slant path using geometric relationships, e.g., the Niell mapping function (Niell, 1996) or the Vienna mapping function (Böhm et al., 2006). The ZTD can be split into a dry, hydrostatic part (zenith hydrostatic delay, ZHD) and a wet part (zenith wet delay, ZWD). Both zenith delay components are obtained through vertical integration of the refractivity indices N_hyd and N_wet for each model layer over the entire model. The hydrostatic refractivity index N_hyd only depends on the air density ρ:

$$\begin{array}{}\text{(8)}& N_{\mathrm{hyd}}=k_{\mathrm{1}}\cdot R_{\mathrm{d}}\cdot \mathit{\rho },\end{array}$$

with the hydrostatic refraction constant k₁=77.6 K hPa⁻¹ and the specific gas constant for dry air R_d=287.05 J kg⁻¹ K⁻¹. The density follows the equation of state for ideal gases:

$$\begin{array}{}\text{(9)}& \mathit{\rho }={\displaystyle \frac{p}{R_{\mathrm{d}}\cdot T_{\mathrm{v}}}},\end{array}$$

with the pressure p and the virtual temperature T_v in each layer. T_v is the equivalent temperature of dry air with the same density as wet air and is computed from the air temperature T and the specific humidity s according to Emeis (2000):

$$\begin{array}{}\text{(10)}& T_{\mathrm{v}}=T\cdot \left(\mathrm{1}+\mathrm{0.608}\cdot s\right).\end{array}$$

The wet refractivity index N_wet is a function of the partial water vapor pressure e and the temperature T in kelvin:

$$\begin{array}{}\text{(11)}& N_{\mathrm{wet}}=k_{\mathrm{2}}{}^{\prime }\cdot {\displaystyle \frac{e}{T}}+k_{\mathrm{3}}\cdot {\displaystyle \frac{e}{T^{\mathrm{2}}}},\end{array}$$

with the refraction constants $k_{\mathrm{2}}^{\prime }=\mathrm{22.1}$ K hPa⁻¹ and k₃=370 100 K² hPa⁻¹ (Bevis et al., 1994). The compressibility factor accounting for non-ideal gas behavior is neglected in this case.

For the vertical integration, the refractive index at each layer multiplied by the layer thickness is summed over all model layers. Above the upper boundary of the ICON-EU model at 22.5 km height, the remaining part of ZHD, being on the order of 7–8 cm, is computed according to Eq. (6), with the pressure and height taken at the top of the model instead of the surface. The contribution of the atmosphere above 22.5 km to the ZWD can be neglected since the water vapor content is close to zero. A similar procedure was applied to determine the zenith delays ZHD and ZWD from radiosonde data.

The total delays ZTD, the sum of ZHD and ZWD as computed from weather model and radiosonde data, are displayed in Fig. 9 and compared to the ZTD estimation from GNSS analyses. One solution is taken from the BKG GNSS Data Center, a routine analysis of station WTZR as part of the of the GREF network (https://igs.bkg.bund.de/dataandproducts/browse, last access: 22 February 2019) using Bernese 5.2 software; the other solution is derived from the Wettzell local array using the in-house analysis software SGSS. The reported values represent the mean and the 68 % confidence interval of the eight Wettzell GNSS stations each being analyzed in three different regional networks. The confidence intervals give a more realistic error estimation and are thus larger than the standard deviations of a single analysis given in the GREF data.

A time series of the different ZTD values is displayed in Fig. 10. All traces show a similar behavior. The GNSS analyses reveal more details as a consequence of the higher sampling rate of 1 h. Taking the radiosonde data as a reference, the DWD model tends towards lower (2–3 mm) ZTD values and the NCEP model towards higher (5–6 mm) ZTD values. The best coincidence with the radiosonde-derived ZTD gives the GNSS solutions with correlation coefficients up to 0.992.

The cloud coverage as recorded by the nubiscope and the global radiation as measured by the pyranometer are displayed in Fig. 11.