The Ocean Carbon States Database: a proof-of-concept application of cluster analysis in the ocean carbon cycle

In this paper, we present a database of the basic regimes of the carbon cycle in the ocean, the “ocean carbon states”, as obtained using a data mining/pattern recognition technique in observation-based as well as model data. The goal of this study is to establish a new data analysis methodology, test it and assess its utility in providing more insights into the regional and temporal variability of the marine carbon cycle. This is important as advanced data mining techniques are becoming widely used in climate and Earth sciences and in particular in studies of the global carbon cycle, where the interaction of physical and biogeochemical drivers confounds our ability to accurately describe, understand, and predict CO₂ concentrations and their changes in the major planetary carbon reservoirs. In this proof-of-concept study, we focus on using well-understood data that are based on observations, as well as model results from the NASA Goddard Institute for Space Studies (GISS) climate model. Our analysis shows that ocean carbon states are associated with the subtropical–subpolar gyre during the colder months of the year and the tropics during the warmer season in the North Atlantic basin. Conversely, in the Southern Ocean, the ocean carbon states can be associated with the subtropical and Antarctic convergence zones in the warmer season and the coastal Antarctic divergence zone in the colder season. With respect to model evaluation, we find that the GISS model reproduces the cold and warm season regimes more skillfully in the North Atlantic than in the Southern Ocean and matches the observed seasonality better than the spatial distribution of the regimes. Finally, the ocean carbon states provide useful information in the model error attribution. Model air–sea CO₂ flux biases in the North Atlantic stem from wind speed and salinity biases in the subpolar region and nutrient and wind speed biases in the subtropics and tropics. Nutrient biases are shown to be most important in the Southern Ocean flux bias. All data and analysis scripts are available at https://data.giss.nasa.gov/oceans/carbonstates/ (DOI: https://doi.org/10.5281/zenodo.996891).

1 Introduction

The ocean carbon cycle plays an important role in controlling the airborne fraction of CO₂ in the atmosphere, thereby regulating the rate of global warming, i.e., the rising temperatures in the Earth's troposphere. However, the ocean carbon cycle is controlled by a plethora of physical, biological and biogeochemical processes over a broad range of temporal and spatial scales. In this paper, we seek to present and assess a data mining/pattern recognition technique, namely cluster analysis, for the purpose of defining the basic regimes, or “ocean carbon states”, that describe the oceanic carbon cycle variability. The goal is to increase our understanding of the marine carbon cycle by revealing patterns and information that other techniques do not provide.

For geophysical applications, climate datasets have inherent complexities that are not easily identifiable in the age of “big” data. Cluster analysis is a highly effective uni- or multi-variate classification method for large, high frequency datasets because it can find structure in a body of complex, geophysical data (Anderberg, 1973; Peron et al., 2014). Clustering seeks to identify the critical modes and natural patterns of a dataset without any training or predetermined spatial–temporal guidelines; therefore, it is an “unsupervised” graph theory method. The merit of a novel, unsupervised method such as clustering is that it can recognize connectivity between multiple variables. This can be understood as connectivity in a temporal sense where cluster analysis can identify joint interannual or seasonal patterns and in a spatial sense where clustering has the power to identify patterns that relate different regions or basins (Jain, 2010; Phillips et al., 2015).

Traditional methods of univariate analysis, such as principal component analysis or spectral decomposition, cannot fully describe important physical states of the climate system or adequately detect change (Hoffman et al., 2011) because these methods neglect interactions between state variables as well as spatial and temporal co-variability. In contrast, cluster analysis has been successfully applied to various dynamical systems in order to extract the organized states and detect change as well as in novel applications of model–data intercomparison (Hoffman et al, 2008). For example, this technique has been used to define atmospheric weather states by identifying cloud regimes (Jakob and Tselioudis, 2003; Rossow et al., 2005; Williams and Webb, 2009; Tselioudis et al., 2013; Bodas-Salcedo et al., 2014; Oreopoulos et al., 2016). Bankert and Solbrig (2015) were able to extract a 3-D cloud representation using cluster analysis. This technique has also been used to characterize water types in lakes (Trochta et al., 2015), hydraulic habitat composition in rivers (Hugue et al., 2016), phenology patterns in forests (Trans Mills et al., 2011), solar variability (Zagouras et al., 2013), ENSO phenomena (Radebach et al., 2013), and regions with characteristic hydrological responses (Halverson and Fleming, 2015), among many other applications.

Beyond identifying regimes, cluster analysis can be useful in model assessment applications, like that of Wood et al. (2015), which used weather states derived from cluster analysis for process studies, satellite calibration, and model evaluation. Both regime identification and model evaluation are the focus of the cluster analysis presented in this paper as well.

Elsewhere in ocean carbon cycle science, clustering-type methods (self-organizing maps and neural networks) have been used to build reconstructions or as regression analysis alternatives for surface ocean pCO₂ (Lefèvre et al., 2005; Telszewski et al., 2009; Sasse et al., 2013; Landschützer et al., 2013, 2014; Nakaoka et al., 2013). Unlike these studies, here we seek to obtain the co-variability maps and conditions of different ocean-related variables and understand where, why and how they change.

Other non-statistical studies, but similar in concept to multivariate regime identification, have focused more on larger-scale geographic variations (Fay and McKinley, 2014; Trochta et al., 2015) than on the regional aspects of the ocean biogeochemistry and its interaction with physical circulation like in the western boundary current regions, in the upwelling zones on the eastern boundaries, and in the eddying field.

The structure of the paper is as follows. Section 2 describes the datasets used in this study, both the observation-based sources as well as the model experiments. Section 3 presents the k-means cluster analysis methodology and application, including discussion of the k-means clustering technique and sensitivity to number of clusters chosen, to binning, and to data normalization. The results of the methodology are provided in Sect. 4. Section 4.1 focuses on how the methodology is applied in observations from the North Atlantic basin. The observed ocean carbon states are then characterized temporally and spatially in order to reveal their physical meaning. Next, the model carbon states are computed and characterized in a similar way to the observations. Using the ocean carbon states, model biases are also discussed and evaluated. Section 4.2 repeats the analysis presented in Sect. 4.1, but now applied to the Southern Ocean. Finally, general discussion and conclusions are provided in Sect. 5. A note about the figures in the paper: some interesting but non-critical figures are offered in the Supplement and are denoted as Fig. S#. All data and analysis scripts are available at the https://data.giss.nasa.gov/oceans/carbonstates/ website (DOI: https://doi.org/10.5281/zenodo.996891).

2 Data

2.1 Choice of variables to represent ocean carbon regimes

One critical question to answer at the onset of any clustering analysis is what key geophysical variables should be used to base the analysis on. For the purposes of this study, we picked sea surface temperature (SST) and partial pressure of CO₂ in the ocean surface water (pCO_2 sw). The rationale for this choice will be explained now. There are two main pathways that determine the ability of the ocean to take up CO₂ (Sarmiento and Gruber, 2006): the chemical disequilibrium, expressed by pCO₂, dissolved inorganic carbon (DIC is the sum of all inorganic carbon species) and nutrients, and the physical processes, such as air–sea interaction (expressed by the wind speed) and ocean circulation (expressed by sea surface temperature and salinity). Greater insight into the ocean's biogeochemical processes that control these pathways can inform the improved use of field measurements, the development of better metrics for model evaluation, and the selection of more suitable parameterizations in climate models in order to provide more accurate predictions. We select pCO_2 sw and SST because they are able to represent a broad range of biogeochemical and physical processes. We use them in cluster analysis to find temporal and spatial patterns in their joint parameter space that can be used to understand CO₂ flux distributions and its fluctuations. Other variable pairs can be alternatively used here; a comparison between choices is set aside for future work.

This study will focus on two oceanic basins, namely the North Atlantic (defined as 80^∘ W to 45^∘ E, 0 to 90^∘ N) and the Southern Ocean (defined as 180^∘ W to 180^∘ E, 90 to 40^∘ S), because of their importance in the global carbon cycle (Takahashi et al., 2009).

2.2 Observation-based data

2.2.1 Air–sea flux of CO₂ and pCO₂, surface wind speed, sea surface temperature and salinity

The 12-month climatology of the air–sea flux is obtained from the Carbon Dioxide Information Analysis Center (LDEO database, NDP-088; Takahashi et al., 2009). It is derived from the difference between surface water pCO₂ (pCO_2 sw), air pCO₂, and the air–sea gas transfer rate. Surface water pCO₂ climatological mean distribution was obtained from 3 million measurements from 1970 to 2007, and normalized to a reference year 2000. The pCO₂ of the air is computed from the GlobalView CO₂ concentration zonal mean, NCAR monthly mean barometric pressure, SST, and salinity. Other variables in the dataset pertinent to this analysis are wind speed (derived from the 1979–2005 climatological mean NCEP-DOE AMIP-II Reanalysis wind speed field), climatological sea surface temperature (from NOAA Climate Diagnostic Center Objective Interpolation), and salinity (from the NODC World Ocean Database 1998). All variables are available as a 12-month climatology at a $\mathrm{4}{}^{\circ }\times \mathrm{5}{}^{\circ }$ resolution.

2.2.2 Nitrate

The nitrate monthly climatology at 1^∘ horizontal resolution is obtained from the World Ocean Atlas 2013 version 2 (Boyer et al., 2013). It is collected from in situ measurements at standard depth levels and is available as annual, seasonal, and monthly climatologies. Nitrate is an essential nutrient that limits the growth of phytoplankton, which is responsible for fixating carbon dioxide from the atmosphere. Therefore, pCO₂ levels in the surface ocean depend partially on the abundance of nitrate.

2.3 Numerical simulations

The NASA-GISS modelE2.1 output used for this analysis comes from five ensemble coupled model simulations of the 20th century with realistic greenhouse gas, aerosol, land use and solar forcing, as used in CMIP5 experiments. The model physics is somewhat different than the modelE2 used in the CMIP5 experiments, mostly due to improved representation of the ocean mesoscale mixing. The physical ocean and the biogeochemistry modules are described in detail in Romanou et al. (2013, 2017). Briefly, here we note that the ocean model is a non-Boussinesq mass-conserving ocean model with 32 vertical levels and $\mathrm{1}{}^{\circ }\times \mathrm{1.25}{}^{\circ }$ horizontal resolution. The vertical coordinate is a stretched z-level coordinate and has a free surface and natural surface boundary fluxes of freshwater and heat that are obtained by the atmospheric model. In addition to advection and turbulent mixing, it also includes a scheme for isopycnal eddy fluxes and isopycnal thickness diffusion. The interactive ocean carbon cycle model consists of a biogeochemical model (NASA Ocean Biogeochemistry Model, NOBM; Gregg and Casey, 2007) and a gas exchange parameterization for the computation of the CO₂ flux between the ocean and the atmosphere (Romanou et al., 2013). Specifically, the air–sea exchange of CO₂ (Sarmiento and Gruber, 2006; Takahashi et al., 2009) is described by Eq. (1):

$$\begin{array}{}\text{(1)}& {\displaystyle }F=\text{kw}{K}_{\mathrm{0}}\left(p{\text{CO}}_{\mathrm{2}\mathrm{atm}}-p{\text{CO}}_{\mathrm{2}\mathrm{sw}}\right),\end{array}$$

where kw is the piston velocity for CO₂ (in m s⁻¹) that depends on the wind speed, K₀ is the solubility coefficient – dependent on sea surface temperature (SST) and sea surface salinity (SSS) (expressed in mole, CO₂ kg⁻¹ atm⁻¹) – and pCO₂ is the partial pressure of CO₂ (Wanninkhof et al., 2013) in the atmosphere (atm) and the surface ocean (sw). Equation (1) describes the chemical disequilibrium of CO₂ in the oceanic and atmospheric reservoirs due to the solubility and biological pumps. As discussed in Sarmiento and Gruber (2006), the pCO_2 sw in Eq. (1) is a function of temperature and salinity, wind speed, DIC, nutrients, and alkalinity (a measure of the excess of bases over acids) which can be expressed as follows:

$$\begin{array}{}\text{(2)}& {\displaystyle }p{\text{CO}}_{\mathrm{2}\mathrm{sw}}=f\left(\text{SST,\hspace{0.17em}\hspace{0.17em}SSS,\hspace{0.17em}\hspace{0.17em}DIC,\hspace{0.17em}\hspace{0.17em}windspeed,\hspace{0.17em}\hspace{0.17em}nutrients,\hspace{0.17em}\hspace{0.17em}alkalinity}\right).\end{array}$$

NOBM utilizes ocean temperature and salinity, mixed layer depth and the ocean circulation fields, and the horizontal advection and vertical mixing schemes obtained from the host ocean model as well as shortwave radiation (direct and diffuse) and surface wind speed obtained from the atmospheric model to produce horizontal and vertical distributions of several biogeochemical constituents. The carbon submodel parameterizes the cycling of carbon through the phytoplankton, herbivore and detrital components, affecting the dissolved inorganic and organic carbon in the ocean and interacting with the atmosphere. Alkalinity is assumed analogous to surface salinity, which is an acceptable approximation for the sea surface but does not take into account changes in the carbonate pump. Temperature and salinity are affected only by physical processes such as circulation, advection, eddy mixing and stirring, and local upwelling/downwelling, while DIC distributions are influenced by all these physical processes and also several biogeochemical processes such as air–sea gas exchange, production by organisms, biological export to depth and remineralization there and nutrient availability in the water column. Atmospheric pCO₂ (pCO_2 atm) is the saturation concentration of CO₂ in equilibrium with a water-vapor-saturated atmosphere at a total atmospheric pressure P and a given atmospheric pCO₂ level:

$$\begin{array}{}\text{(3)}& {\displaystyle }p{\text{CO}}_{\mathrm{2}\mathrm{atm}}={\displaystyle \frac{P}{P^{\mathrm{0}}}}{\text{CO}}_{\mathrm{2}}^{\mathrm{0}},\end{array}$$

where P₀=1 atm and [CO₂]⁰ is the saturation concentration at 1 atm total pressure.

The gas transfer velocity is given by

$$\begin{array}{}\text{(4)}& {\displaystyle }\text{kw}=c{\left({\displaystyle \frac{\mathit{\text{Sc}}}{\mathrm{660}}}\right)}^{-\mathrm{1}/\mathrm{2}}{u}^{\mathrm{2}},\end{array}$$

where u is the surface wind speed and c is the piston velocity coefficient taken here equal to $\mathrm{0.337}/(\mathrm{3.6}\times {\mathrm{10}}^{\mathrm{5}})$. The value of c has been agreed upon by the Ocean Carbon Model Intercomparison Project, phase II (OCMIP-II) so that the global, annual mean gas transfer coefficient for carbon dioxide (kw, K₀) is equal to 0.061 mol m⁻² yr⁻¹ (µatm)⁻¹ for preindustrial times. Sc, the Schmidt number, is computed using the temperature of the host ocean model following Wanninkhof (1992). The gas transfer velocity kw is computed only over open water. The solubility of CO₂ in the water K₀ is also parameterized based on OCMIP using prognostic temperature, salinity and sea level pressure. In these model runs, the global average of the atmospheric concentration of CO₂ follows the Mauna Loa measurements (Dlugokencky and Tans, 2014), although regionally atmospheric CO₂ is allowed to vary due to the distributions of the ocean sources and sinks.

The five ensemble member runs were averaged into one ensemble mean to account for the intrinsic climate variability that is not adequately resolved in climate models of low spatial resolution. The model output for the years 1995–2005 was then averaged again to produce a 12-month climatology for the purpose of direct comparison with the observationally based data in the Takahashi database.

The model output and the observational data were interpolated onto the same grid, which is the Takahashi ocean grid at $\mathrm{4}{}^{\circ }\times \mathrm{5}{}^{\circ }$ resolution, with no Arctic Ocean, and the ocean mask was conformed across all observational and model datasets.

In the rest of the paper, some conventions with regards to nomenclature should be noted. Firstly, the Takahashi carbon flux, pCO₂ and ancillary data as well as the nitrate climatology will be referred to as “observations”, for brevity, keeping in mind that they are really observation-based estimates and not direct observations. Secondly, “model” will exclusively refer to the numerical simulations using the NASA-GISS climate model, and by “algorithm”, “method” or “technique” we will refer to the clustering technique.

All data products are available in the Ocean Carbon States Database (https://data.giss.nasa.gov/oceans/carbonstates/).

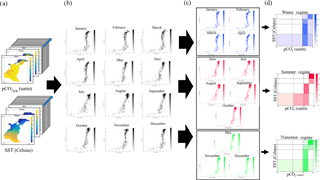
Figure 1 Schematic diagram of the clustering methodology used in this paper: (a) 12-monthly mean climatological year data of two variables, pCO₂ and SST, (b) monthly 2-D histograms, (c) clustering of the 2-D histograms into groups by similarity in the bivariate distributions, and (d) clusters resulting when k=3 is assumed.

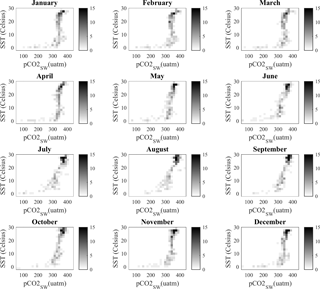
Figure 2 Monthly 2-D histograms of partial pressure of CO₂ in the surface water (pCO_2 sw) and sea surface temperature (SST) in the North Atlantic (defined as 80^∘ W to 45^∘ E, 0 to 90^∘ N) from the Takahashi observational dataset. The horizontal axis is pCO_2 sw (uatm) and the vertical axis is SST (^∘C). The bin interval is 15 uatm and 1.6 ^∘C. The color bar describes the actual frequency of occurrence of each bin.

3 Methodology

A schematic diagram of the methodology is presented in Fig. 1. First, the 2-D histograms pCO₂-SST are computed from the climatological data, then the histograms are clustered using a statistical method, the k-means clustering method, and finally the regimes or “ocean carbon states” are obtained. The methodology steps will be explained in detail below, using as an example the North Atlantic basin data.

3.1 pCO₂-SST 2-D histograms

pCO_2 sw values in the North Atlantic span the range 50–450 uatm, while sea surface temperatures range between −2 and 30 ^∘C. The 2-D histograms (Fig. 2) show the highest frequency of occurrence for pCO_2 sw values in the range of 300–400 uatm and temperatures in the range of 10 to 30 ^∘C. Certain months (December, January, February and March) show a higher frequency of occurrence of cold temperatures (−2 to 2 ^∘C) and low pCO_2 sw (50–300 uatm) than others. Figure 2 also reveals that certain histograms appear similar in shape; for example, January–April exhibit an S-shaped curve and no tilt, while June–September exhibit a diagonal tilt that reflects a tendency for higher temperatures to co-locate with higher pCO_2 sw values. This being a small dataset of only 12 2-D histograms, one could easily sort them into groups of similar shape just by visual inspection only. The methodology presented in this paper seeks to more mechanistically identify these groups, so that it can be confidently applied to larger and more complex datasets. We will call those organized groups, clusters or regimes or “ocean carbon states”.

It is noted here that despite the broad range of values for both variables, the 2-D histograms are very similar regardless of the number of bins chosen for each of the variables.

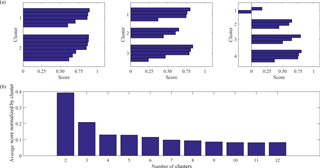
Figure 3 (a) Scores for each cluster analysis of observational data in the North Atlantic for k=2, k=3, k=4, where cluster k is the predetermined number of clusters and each bar represents the score per 2-D histogram. (b) Average scores for each cluster analysis with increasing k, from $k=\mathrm{2},\mathrm{\dots },\mathrm{12}$, normalized by the number of clusters k.

3.2 k-means clustering

The k-means clustering algorithm (Anderberg, 1973; Jakob and Tselioudis, 2003) partitions the 2-D histograms of pCO₂-SST shown in Fig. 2 into a predefined number k of groups, called clusters. In the first step of the algorithm, k histograms are randomly selected and are considered the centroid of each of the k clusters. Each other histogram in the input dataset is then assigned to its nearest centroid by computing the Euclidean distance of each bin of the 2-D histogram from the same bin of the centroid. The procedure is repeated an N number of iterations, each time the centroid of the resulting group is recalculated, if doing so reduces the sum of the distances of each histogram to the centroid. This iterative procedure stops when the squared distance between the mean of each cluster and all the 2-D histograms assigned per cluster is minimized (Jain, 2010). More than one iteration (N) is necessary to have convergent clustering results because each analysis initializes at a random cluster centroid. In this paper, convergence is reached after 10 iterations, if not fewer (Fig. S1 shows how this is determined for the example of the North Atlantic basin).

3.3 Sensitivity to predefined number of clusters

To ensure that the chosen number of clusters, k, is representative of the system, typically one needs to repeat the technique for various values of k, and, using visual inspection, select the optimal value for k when the resulting clusters become repetitive or contain no additional information. Objective methods have been proposed (e.g., Bankert and Solbrig, 2015), where the average radius of each cluster (the distance from the centroid to the most distant member within a cluster) is computed for decreasing k. Bankert and Solbrig (2015) found that when the number of clusters falls below the optimal k, the average radius grows rapidly. We employ a similar methodology here. First, we use a scoring algorithm that computes the distance of each 2-D histogram from the centroid of its cluster. The higher the score is, the closer the 2-D histograms are to the centroid. The maximum score is 1, which indicates a perfect match. Negative or low values indicate poorly matched histograms that are the farthest from the centroid in the cluster. We run the scoring algorithm for k=2 through k=12, since we have 12 2-D histograms, and therefore there can be up to 12 clusters. Figure 3a shows the scores only for k=2, k=3, and k=4 as examples of the output of the scoring algorithm. We find that for k=2 and k=3 all 2-D histograms are well matched within a cluster (i.e., all scores are high), whereas for k=4 there is 1 month with a negative score. To further summarize the scoring results, we introduce a “sensitivity criterion” to the predetermined number of clusters, k, in which we average all scores for each k and normalize by k. The results are shown in Fig. 3b, where we note that the averaged normalized score for k=2 is 0.4, and it then quickly drops to 0.2 for k=3 and to 0.1 for k=4, and it plateaus after that. We choose as the optimal number of clusters the k with the highest score and no significant change in the normalized averaged score thereafter. This choice implies that any reorganization of the 2-D histograms within more than three clusters will not produce any “tighter” clusters, i.e., clusters where the members are closer together. We must note here that the method is not entirely objective, as one always needs to visually inspect the clusters themselves and ensure that the choice of k is indeed the best one.

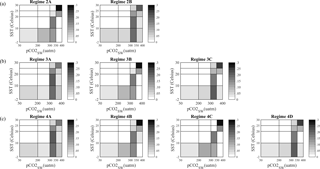
Figure 4 Cluster analysis output (regimes) for (a) k=2, (b) k=3, and (c) k=4 for the North Atlantic, from the Takahashi observational dataset. The color bar represents the relative frequencies of occurrence of each value-pair interval; i.e., the frequencies are divided by the total number of frequencies per regime.

3.4 Data normalization

As noted earlier, pCO₂ and SST have a broad range of values. Specifically, pCO₂ values vary by about 2 orders of magnitude between 50 and 450 uatm, and SST by 1 order of magnitude between −2 and 30 ^∘C. It is customary in applications of statistical techniques such as clustering to normalize the data (subtract the mean and divide by the standard deviation) in order to force both datasets to be in the same range of values. However, this is not always necessary (Anderberg, 1973, p. 13; Kaufman and Rousseauw, 2005, p. 11). In our case, we are not clustering each variable separately in order to determine regression coefficients (as in Lefèvre et al., 2005). Rather, we are clustering the 2-D histograms and comparing them, in order to obtain groups of similar patterns. In addition, clusters represented in normalized data are not as easily understood physically and as well represented on geographical maps. Therefore we choose not to normalize the data for the purposes of this study.

4 Results

4.1 The North Atlantic Ocean carbon states

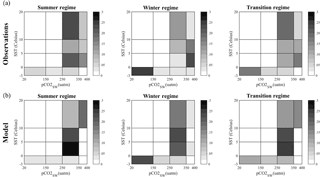
Figure 4 depicts the regimes for k=2, k=3, and k=4. When only two clusters are predefined, i.e., for k=2, the first cluster (Regime 2A, Fig. 4a) is dominated (30 % of the time) by pCO₂-SST pairs in the ranges of 350–400 uatm and 25–30 ^∘C. The second cluster (Regime 2B) is dominated (20 %) by pCO_2 sw values within 300–350 uatm and SST values in the range −2 to 20 ^∘C. When we choose more clusters initially, i.e., for k=3, Regime 3B is very similar to Regime 2A and Regime 3C is analogous to Regime 2B, in the sense that the regimes have analogous bins of the highest frequencies. Regime 3A is a new state that was unresolved in k=2, but is not similar to 3B or 3C. For k=4, Regimes 4B and 4C appear to be almost equivalent, and both derived from Regime 3B, which probably indicates that there is no new information gained by requiring four clusters. Similar visual inspection of the results for k > 4 confirms our more objective analysis result that k=3 is the optimal number of clusters in the pCO₂-SST space in the North Atlantic basin. It should be noted here that because we implement k clustering in the 2-D histograms and not the raw data, there is really no change in the results if we use a different number of bins in the histograms or if we use normalized data.

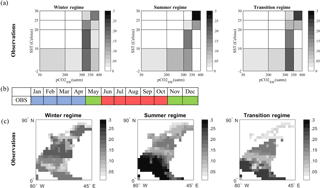
Figure 5 (a) Ocean carbon states (regimes) in observation-based data of the North Atlantic. (b) Monthly attribution of each ocean carbon regime in the Takahashi observational dataset. Temporal attribution is based on the distance of each monthly 2-D histogram to the centroid of each cluster. Each color represents a different regime: blue denotes the cold months' regime (winter regime), red the warm months (summer regime) and green the May/November–December transition regime, since this is more a mix of the other two. (c) Regional attribution of each regime depicted in (a). The colors in (c) correspond to the ones in (a), i.e., to the frequencies of occurrence of each bin (value pair) in the clusters of (a).

4.2 Temporal attribution for the North Atlantic carbon states

In order to characterize the ocean carbon states obtained in the previous section, we perform a temporal attribution analysis by determining when each cluster occurs. This is possible because for each cluster (regime), the k-means analysis routine computes the distance of every 2-D histogram in that cluster to the cluster's centroid. Since each 2-D histogram is associated with a certain month in the climatology, we are able to associate each cluster with certain months. Figure 5b shows that in the North Atlantic basin, regime 1 is represented by months January, February, March, and April and we call this the “winter regime”; regime 2 occurs during June, July, August, September and October and we will thus call it the “summer regime”; regime 3 occurs in May, November, and December and we will call this the “transition regime” because it reflects a mixed season in between the winter and summer regimes. Not surprisingly, these resulting regimes align themselves fairly well with the boreal winter and summer seasons in the North Atlantic. The cold season (winter regime) includes March and April but not November–December, which are included, rather, in the transition regime. The warm season (summer regime) includes the months between June and October, again broader than the typical boreal summer. It is not surprising that we recover the seasonal cycle from the 12-month climatology, and probably because our domain is the entire North Atlantic, from the Equator to the subpolar regions, these seasons are broader including months from the spring and fall, since the length of each season is different at different latitudes.

4.3 Spatial attribution of the North Atlantic carbon states

Next, we describe the geographical distribution of each regime (Fig. 5c). To do so, the frequencies of occurrence associated with each pCO₂-SST bin in Fig. 5a are averaged over the months in each regime and mapped on the North Atlantic basin. We find that in the winter regime, the dominant value pairs (300–350 uatm and 10–20 ^∘C) are found in the subtropical North Atlantic. In contrast, the dominant range of pCO₂-SST pairs in the summer regime occurs in the tropics (values 350–400 uatm and 25–30 ^∘C). The transition regime shows a mix of the winter and summer regimes.

We conclude that the ocean carbon states determined by a 12-month climatology of surface ocean pCO₂ and SST are characterized by a cold season where most persistent value pairs occur in the subtropical North Atlantic and the subpolar region. In the warm season, however, the most persistent value pairs occur in the tropical Atlantic. For more complex datasets, e.g., when interannual variability is included, we expect to be able to detect regimes that correspond to processes controlled by the El Nino–Southern Oscillation (ENSO) or the North Atlantic Oscillation, for example.

4.4 The NASA-GISS climate model North Atlantic carbon states

Next we obtain the ocean carbon states from the GISS model simulations, following here the same methodology as for the observations. We are interested in understanding how similar the model regimes are to the observed ones we found earlier. As described in Sect. 2.3, we construct the ensemble mean climatologies for pCO_2 sw and SST for the period 1995–2005 from five simulations of Earth's historical climate of the 20th century performed with the NASA-GISS climate model. We then obtain the 12-monthly 2-D histograms from the model climatology and, using the same binning groups as in the observations, we obtain the model clusters. It should be noted here again that because we are actually clustering the 2-D histograms and not the raw data, our clusters are not sensitive to the number of bins or to normalization of the datasets prior to cluster analysis. The sensitivity criterion (discussed in Sect. 3) for the model clusters is not as clear as in the case of the observations (Fig. 6). Note that there is a plateau after k=5 and thus it appears that 5 would be a more suitable choice for k. However, as seen in Fig. 6a, some of the additional regimes include only one monthly 2-D histogram. We therefore chose here k=3, recognizing that the model clusters have larger uncertainty. In a larger dataset that includes interannual variability, more than a single 2-D histogram would potentially be assigned to a regime, reducing that uncertainty.

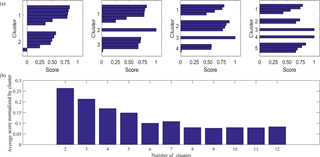
Figure 6 (a) Scores for each cluster analysis of the GISS model data in the North Atlantic for k=2, k=3, k=4, k=5, where cluster k is the predetermined number of clusters and each bar represents the score per 2-D histogram. (b) Average scores for each cluster analysis with increasing k, normalized by the number of clusters k.

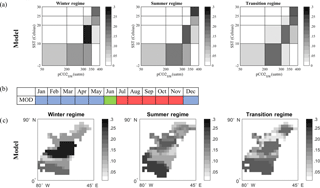
Figure 7 (a) Ocean carbon states (regimes) in the North Atlantic from the GISS model output. (b) Monthly attribution of each ocean carbon regime. Temporal attribution is based on the distance of each monthly 2-D histogram to the centroid of each cluster. Blue denotes the cold month regime (winter regime), red the warm months (summer regime) and green the transition regime (only June), since this is more a mix of the other two. (c) Regional attribution of each regime depicted in (a). The frequencies of occurrence of each bin (value pair) in the clusters of (a) are mapped onto the North Atlantic grid.

Figure 7a shows the ocean carbon states for k=3, while Fig. 7b characterizes their temporal occurrence: the model winter regime corresponds to the months December, January, February, March, April, and May; the summer regime corresponds to the months July, August, September, October, and November; the transition regime corresponds only to June. There is therefore good agreement with the regimes from observations (Fig. 5b). The model winter regime is somewhat broader than that observed by 2 months (December and May), while the model summer regime lags by 1 month (starts in July, while in the observations it starts in June).

The regimes (clusters) themselves are similar to the observations (comparing Figs. 5a and 7a) in that the same bins of most likely values are identified but with somewhat different frequencies of occurrence. As an example of comparison between the temporal regimes, for the winter regime both the model and the observations show that the dominant pairs are in the range of 300–350 uatm and 20–25 ^∘C, at 30 and 25% relative frequency. However, other weaker pairs are not well represented in the model, e.g., the range 50–200 uatm and −2 to 10 ^∘C. During the winter regimes, the highest frequency of occurrence (25 %) is for the pair of values 300–350 uatm and 10–20 ^∘C, whereas in the model the same pair of values is found 30 % of the time. Similarly, the summer and transition regime highest frequency pairs are well simulated. In contrast, the value pairs 200–350 uatm for very cold temperatures are not well represented in the model.

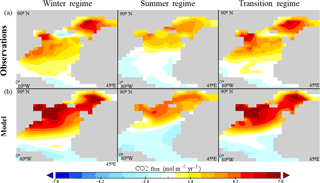
Figure 8 Composites of the CO₂ flux field over the observed regimes for (a) the observations and (b) the model. The composite fields are computed as averages of the field over the months included in each regime. Both the observations and the model data are composited over the same months as determined by the temporal attribution of the observations dataset, shown in Fig. 5b. Blue shades indicate outgassing, and red shades indicate uptake.

We also find (Fig. 7c) that in the winter regime, the dominant value pairs (300–350 uatm and 10–20^∘C, identified in Fig. S2) are found in the subtropical North Atlantic, with higher frequency in the model (darker shading) than in the observations. The GISS model however underestimates the frequency of occurrence of the value pairs in the subpolar region (values 50–350 uatm and −2 to 10 ^∘C, identified in Fig. S2). In contrast, the dominant range of pCO₂-SST pairs in the summer regime occurs in the tropics (values 350–400 uatm and 25–30 ^∘C; Fig. 7c) and is of higher frequency in the observations than the model. In other words, the model underestimates the extent of the tropical summer regime but reproduces well the other parts of the summer regime. The transition regime shows a mix of the winter and summer regimes for both observations and model. The model results in this regime indicate higher frequency in the subpolar region than in the observations.

4.5 Model North Atlantic air–sea flux of CO₂ error analysis and bias attribution

The ocean carbon states can provide a framework for model assessment against the observations. In this section we seek to identify biases in the simulated flux of CO₂ and attribute them to leading biases in physical and biogeochemical processes.

In the previous section we used the same methodology as in the observations to obtain independently the model regimes and assess how different they are. However, when we want to identify the causes of the model biases, we have to use the observed regimes as the basis of the comparison and assign the model data to the observed regimes, by averaging the model data over those months that the observed regimes occur (Fig. 5b). This approach was highlighted in Williams and Webb (2009) for general circulation model evaluations of the cloud regimes.

Figure 8 depicts the air–sea flux of CO₂ composited over the observed temporal regimes in both observations (Fig. 8a) and model output (Fig. 8b). In the winter regime, model outgassing (in shades of blue) is confined only to the tropics, whereas in the observations there is also a tongue of outgassing at about 60^∘ N. Similarly, in the transition regime, the model has a more extended uptake region in the subpolar North Atlantic than in the observations. While the summer regime is better represented in the model than the other two regimes, all three regimes show that model uptake is stronger than in observations at mid and high latitudes and that outgassing is also stronger in the model at mid to low latitudes.

To trace the source of model biases in the air–sea flux of CO₂ we need a better understanding of the physical or biogeochemical processes that control the air–sea flux of CO₂ in the model. Using the clustering analysis results from the previous section, we can investigate the underlying processes that might be responsible for the bias.

The process attribution is performed using a Taylor expansion of the model bias as shown in Eq. (5). The model flux bias, ΔF, depends on the biases of pCO_2 sw, SST, salinity (SSS) and wind speed (wspd) such that

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{\Delta }F\sim {\displaystyle \frac{\partial F}{\partial p{\text{CO}}_{\mathrm{2}\mathrm{sw}}}}\mathrm{\Delta }p{\text{CO}}_{\mathrm{2}\mathrm{sw}}+{\displaystyle \frac{\partial F}{\partial \text{SST}}}\mathrm{\Delta }\text{SST}\\ \text{(5)}& {\displaystyle }& {\displaystyle }+{\displaystyle \frac{\partial F}{\partial \text{SSS}}}\mathrm{\Delta }\text{SSS}+{\displaystyle \frac{\partial F}{\partial \text{wspd}}}\mathrm{\Delta }\text{wspd},\end{array}$$

where Δq is the bias of the variable q, defined as the root mean squared error (RMSE) between the observations and the model, and q is any of the variables $\left\{p{\text{CO}}_{\mathrm{2}\mathrm{sw}},\text{SST},\text{SSS},\text{wspd}\right\}$. $\frac{\partial F}{\partial q}$ is a weight term that represents dependence of the flux on that variable and is determined by the slope of a linear fit in the scatter plot of the flux F with each variable q for each carbon state. Since the North Atlantic basin is a very broad basin, both zonally and meridionally, and because the carbon states' regional distribution (Fig. 5c) is quite complex, we identify areas where the linear fits will be more appropriate approximations of the {F,q} relationships. The subpolar region where the value pairs are −2 to 10 ^∘C and 50 to 350 uatm, a subtropical region (10 to 20 ^∘C, 300 to 350 uatm), and a tropical region (20 to 30 ^∘C, 300 to 400 uatm) are demarcated in Fig. S2. Results of the regional scatter plots and the linear fit for each regime are shown in Fig. S3 and are synthesized in Fig. 9. Each contribution term (each term on the right-hand side of Eq. 5) is calculated from the multiplication of the weights and the RMSEs. Figure 9 then shows that over most of the North Atlantic, the flux biases are attributed mainly to errors in the pCO_2 sw, although in subpolar regions other terms such as salinity biases and wind speed biases become important. It therefore makes sense to further investigate biases in pCO_2 sw and the processes these are attributed to, as presented in Eq. (2).

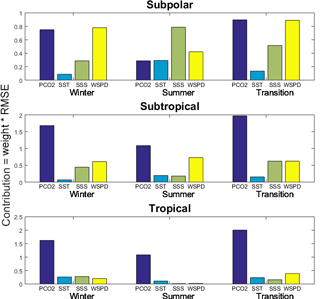
Figure 9 Contributions of each of the variables pCO₂, SST, SSS, and WSPD to the overall air–sea flux ΔF bias. The contributions are computed as the products of the weights and the RMSEs of each variable q as described in Eq. (5). See the text for a detailed explanation.

Similarly to Eq. (5),

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathrm{\Delta }p{\text{CO}}_{\mathrm{2}\mathrm{sw}}\sim {\displaystyle \frac{\partial p{\text{CO}}_{\mathrm{2}\mathrm{sw}}}{\partial \text{SST}}}\mathrm{\Delta }\text{SST}+{\displaystyle \frac{\partial p{\text{CO}}_{\mathrm{2}\mathrm{sw}}}{\partial \text{SSS}}}\mathrm{\Delta }\text{SSS}\\ \text{(6)}& {\displaystyle }& {\displaystyle }+{\displaystyle \frac{\partial p{\text{CO}}_{\mathrm{2}\mathrm{sw}}}{\partial \text{WSPD}}}\mathrm{\Delta }\text{WSPD}+{\displaystyle \frac{\partial p{\text{CO}}_{\mathrm{2}\mathrm{sw}}}{\partial \text{NITRATE}}}\mathrm{\Delta }\text{NIT}.\end{array}$$

We perform the Taylor expansion of the bias for each of the regimes that we computed, calculating the weights and RMSEs in the same way as described for CO₂ flux biases. The estimates of the linear fit slopes of the scatter plots are shown in Fig. S4 and the composites of the contributions in Fig. 10.

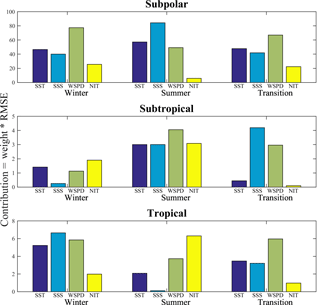
Figure 10 Contributions to the pCO_2 sw bias in the model from SST, SSS, wind speed (WSPD) and nitrate (NIT) in the winter, summer, and transitional regimes. Contributions are computed as in Fig. 9 (see details in the text). The entire North Atlantic is differentiated into subpolar, subtropical, and tropical regions to better account for regional differences in the model biases and obtain a better linear fit for the computation of the weights in Eq. (6).

Overall Fig. 10 shows that the biases in the subpolar region are larger than anywhere else in the North Atlantic basin, as the contributions to the bias in pCO_2 sw are an order of magnitude larger there. Specifically, in the subpolar region, wind speed biases emerge as responsible for the winter and transition regime biases in pCO_2 sw, while salinity biases dominate the summer bias in pCO_2 sw. In the winter and transitional months, the quasi-cyclonic subpolar gyre, driven by energetic winds and wind outbreaks, leads to Ekman divergence in the surface layer that controls the pCO_2 sw biases near the coast. At the same time, winter-time convective mixing is responsible for biases in the strength of the Meridional Overturning Circulation that are known to influence open ocean pCO_2 sw (Romanou et al,. 2017). In the summer regime, GISS model sea-ice concentration is higher than observed; hence, melting will lead to significant surface salinity biases. Inaccurate model representation of the magnitude and fluctuations of the cyclonic wind stress curl as well as the sea-ice retreat and associated salinity changes are probably responsible for deficient physical characterization of the model ocean circulation, which would result in misrepresentations of the pCO_2 sw and thus the CO₂ flux in the model.

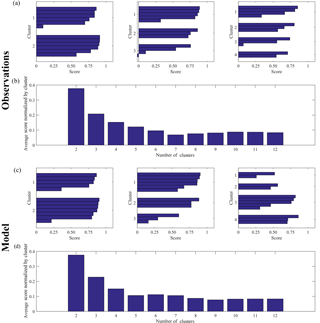
Figure 11 (a) Scores for each cluster analysis for k=2, k=3, k=4 for the observational data in the Southern Ocean where cluster k is the predetermined number of clusters and each bar represents the score per 2-D histogram. (b) Average scores of each clustering analysis for increasing k, from k=1 to k=12. (c) Scores for each cluster analysis for k=2, k=3, k=4 for the model data in the Southern Ocean. (d) Average scores of each clustering analysis for increasing k.

In the subtropics, nitrate is found to be the largest contributor for the winter regime biases, wind speed is the main contributor in the summer, and salinity is the main contributor for the transition regime. The subtropics are characterized at the surface by anticyclonic circulation and a strong western boundary current, the Gulf Stream. Gyre subduction supports downwelling which brings nutrients and pCO₂ to depth. Nitrate utilization by ocean biology during the winter regime is probably inaccurate in the model, while wind speed biases are known to be larger in the summer than the winter regime in the model.

In the tropics, biases in wind speed, nitrate and salinity are again found to be important. Here, nitrate biases, which are relatively higher in oligotrophic regions (Arteaga et al,. 2015), are probably due to misrepresentation of nitrogen fixation in the GISS climate model. Wind speed and salinity biases are associated with well-known biases in the intensity and position of the Inter Tropical Convergence Zone (ITCZ) that controls cloudiness, temperature gradient, and rainfall. The ITCZ moves north in the summer and south in the winter; therefore, a wind speed bias in the transition regime in the model could be explained by an inaccurate model reproduction of how the ITCZ affects the wind during its transitional movement. The ITCZ increases precipitation, thus decreasing salinity; therefore, how salinity changes by season as a result of the shifting ITCZ could explain the winter regime bias.

4.6 The Southern Ocean carbon states

The application of cluster analysis in the Southern Ocean is presented here similarly to in the North Atlantic, with the purpose of examining whether the technique will also be able to identify some known aspects of the Southern Ocean carbon cycle. For brevity, though, the observation-based and model regimes will be presented alongside one another and will be followed by the model-error attribution analysis.

As done for the North Atlantic basin, we look at probability density distributions of observations in the Southern Ocean which show that both SST and pCO_2 sw exhibit a broad range of values. Temperatures range between −3 and 20 ^∘C, whereas pCO_2 sw values span 20 to 400 uatm. The 12-monthly 2-D histograms of pCO_2 sw and SST in the Takahashi dataset are shown in Fig. S5.

Figure 11a shows the scores of each regime for k=2, 3, and 4 and Fig. 11b the results of the sensitivity criterion to the choice of k. Following the criterion established in Sect. 3, the largest score change is for k=3 and k=4. However, Fig. 11a shows that the overall score is better for k=3, because more months have larger individual scores, with the exception of 1 month (November) which has a slightly negative score. Additionally, visual inspection of apparent patterns in the 12-monthly 2-D histograms (Fig. S5) also corroborates the choice of k=3 as the optimal value for the number of clusters. Again, the small climatological dataset leads to some uncertainty in determining k.

A value of k=3 is also chosen for the model analysis based on Fig. 11c and 11d, which show that this is also the optimal number of clusters. There is added ambiguity in the choice of k here, in addition to that due to the small dataset, which arises from the fact that the Southern Ocean is a very broad basin zonally and different processes become important in different regions more so than in the narrow North Atlantic basin, which make the choice of k not as clear as it was in the North Atlantic.

The observed and model ocean carbon states are shown in Fig. 12. In the summer regime, which includes January, February and March (see Fig. 13 and the explanation below), the highest frequency pair values (i.e., the most persistent pairs) are found around 20 % of the time in the observations and 25 % of the time in the model for the ranges of 250–350 uatm and 0–5 ^∘C. Another range of pair values which also shows a high frequency of occurrence (25 %) is found for warmer temperatures (10–20 ^∘C) and the same range of pCO₂, but the GISS model misplaces it towards higher values of pCO₂ (350–400 uatm). The winter regime comparison shows that the model captures the low pCO₂, low temperature state (20–150 uatm, −3 to 0 ^∘C) well (30 % of the time in observations and in the model). The mid-range pCO₂, high temperature state (250–350 uatm, 10–20 ^∘C) is not as well represented in the model. The observations there show the highest frequencies of occurrence for higher pCO₂ (350–400 uatm), in contrast to the model for lower pCO₂ (250–350 uatm). Comparison between the transition regimes reveals much less correspondence between observations and the GISS model, considering the high frequency states in observations are quite different than in the model (e.g., observations of high frequency states: 20–150 uatm, −3 to 0 ^∘C; 250–350 uatm, 10–20 ^∘C; 350–400 uatm, 0–5 ^∘C; model high frequency state: 250–350 uatm, 0–10 ^∘C).

Figure 12 Comparison between the regimes in (a) the observations and (b) the model output.

4.6.1 Temporal attribution for the Southern Ocean carbon states

Temporal attribution, which is estimated using the method described in Sect. 4.1, is shown for both the model and the observations in Fig. 13. Note that all subsequent analysis considers the austral seasons when referring to “winter” and “summer”. The temporal attribution shows that the observations and model data are clustered in regimes that correspond to almost the same months. The only difference is that November is accounted for in the transition regime for the observations as opposed to the winter regime for the model. It is noted, however, that November is technically a “poorly matched” 2-D histogram in the observation cluster routine, as discussed earlier.

Figure 13 Monthly attribution of each ocean carbon regime in observations and the GISS climate model. Temporal attribution is based on the distance of each monthly 2-D histogram to the centroid of each cluster. Referring to austral seasons, blue denotes the cold month regime (winter regime), red the warm months (summer regime) and green the transition regime, since this is more a mix of the other two.

4.6.2 Spatial attribution of the Southern Ocean carbon states

In order to further explain the model and observed Southern Ocean regimes shown in Fig. 12, the frequencies of occurrence of each bin in the cluster are mapped onto the Southern Ocean regions (Fig. 14), where geographic nomenclature similar to that in Orsi et al. (1995) is used. In the coastal Antarctic divergence zone, SST varies within −3 to 3 ^∘C and pCO₂ 20–250 uatm, in the Antarctic convergence zone SST ranges within 3–10 ^∘C and pCO₂ 250–400 uatm, and in the subtropical convergence zone SST lies within 10–20 ^∘C and pCO₂ 250–400 uatm. Despite the strong temporal attribution agreement between the model and the observations, the regional attributions show much less correspondence. For example, in the summer regime, the observations show the highest frequency of occurrence between 250–350 uatm and 10–20 ^∘C along the subtropical convergence zone (roughly along 40^∘ S), while the highest frequency of occurrence for the model is for the pair 250–350 uatm and 0–5 ^∘C, occurring in the coastal region (poleward of the divergence zone along 60^∘ S). In the winter regime, both observations and the GISS model show the highest frequency of occurrence for the value pairs nearest to the coast where the pCO₂ is low and the temperatures coldest (20–150 uatm and −3 to 10 ^∘C). Further offshore, the model highest frequency values occur for lower pCO₂ (250–350 uatm) than in the observations (350–400 uatm). Lastly, in the transition regime, the model shows a much higher persistency of values in the range (250–350 uatm and 0–10 ^∘C) than in the observations.

Figure 14 Regional attribution of each regime for k=3 in the Southern Ocean in (a) the observations and (b) the GISS model simulations. Each spatial grid point for every month is associated with its relative frequency of occurrence in the cluster output, and then the months are averaged per regime to output the average frequency of occurrence in each regime. Model regimes are calculated using the monthly groups identified by the observations' temporal attribution.

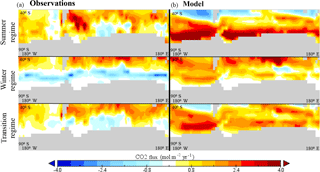
Figure 15 Composites of the CO₂ flux field over the regimes in the Southern Ocean for (a) the observations and (b) the GISS model. Both the observations and the model data are composited over the same months as determined by the temporal attribution of the observed regimes. Blue shades indicate outgassing, and red shades indicate uptake.

It is therefore evident that the GISS model does not reproduce well the observed ocean carbon states in the Southern Ocean. There is a tendency to persistently underestimate pCO₂-SST values closer to the coast and overestimate it near the subtropical convergence zone, during the warm season, whereas, during the cold season, the model captures well the divergence zone regime but the errors further offshore switch: the model now overestimates pCO₂-SST value-pair frequency of occurrence in the Antarctic convergence zone but is performing better in the subtropical convergence zone. The transition regime is not well represented, indicating that not enough regimes are chosen to adequately describe ocean carbon states in this small dataset.

4.6.3 Model Southern Ocean air–sea flux of CO₂ error analysis and bias attribution

Comparing the CO₂ flux composites on the observed regimes (Fig. 15) shows significant discrepancies between observations (Fig. 15a) and model (Fig. 15b). To better understand where these discrepancies come from, we perform an error attribution analysis, as in Sect. 4.1 above. In the summer regime (January through March), outgassing in the model is restricted to the subtropical convergence zone, whereas in the observations it is more localized and closer to Antarctica. At the same time, model uptake is stronger, confined to the coast and over a broader area than in the observations. This is consistent with the result from the previous section, where the model underestimates pCO₂ and SST in the Antarctic convergence zone. In the winter regime (June through October), the entire model basin is a sink for CO₂, whereas in the observations there is a zonally confined outgassing belt south of 50^∘ S and an uptake belt north of it. Again, this result is consistent with the earlier finding that the model winter regime is closer to the observed near the Antarctic coast. The transition regime shares a mix of the same discrepancies as in the summer and winter regimes.

Bias attribution is computed for the three zonally defined regions indicated in Fig. S6. Based on the bias computations in Eq. (5) for pCO_2 sw, SST, salinity, and wind speed with respect to CO₂ flux, pCO_2 sw is again shown to be the driving variable in most of the flux biases in the Southern Ocean (Fig. S7; Fig. S8 for scatter plots). We therefore seek to understand the processes that control the pCO₂ biases in the model, using the Taylor expansion in Eq. (6) (Fig. 16; Fig. S9 for scatter plots).

For almost all regimes and regions, biases in nitrate are large partly because of a lack of a closed, state-of-the-art nitrogen cycle representation in the climate model. On the other hand, observations are too scarce in the region, due to inclement weather and biases to specific seasons, so there is large observational uncertainty associated with the Takahashi climatology in the Southern Ocean. The model skill would be more adequately assessed as more in situ measurements are made (e.g., from the Southern Ocean Carbon and Climate Observations and Modeling, SOCCOM, experiment; Johnson et al., 2017). Nevertheless, the model underestimates surface nitrates in the Southern Ocean in particular because of a large nitrate deficit in the subsurface ocean which upwells in the subantarctic zone and flows into the Antarctic Circumpolar Current region. This is related to processes such as denitrification and accurate remineralization in the deep ocean. SST is the second-most dominating variable for biases in the coastal Antarctic. Inspection of the model biases shows that south of 70^∘ S the model water column is colder than in observations; hence, upwelling there will bring colder waters near the surface. Interestingly, surface salinity biases are relatively very important in the region south of the subtropical convergence zone, which suggests that a study of water mass formation in that region in the model and the observations would better explain the biases.

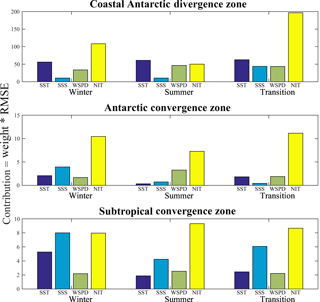
Figure 16 Contributions to the pCO_2 sw bias in the model from SST, SSS, wind speed (WSPD) and nitrate (NIT) in the winter, summer, and transitional regimes. The Southern Ocean is differentiated into the coastal Antarctic divergence zone (roughly polewards of 60^∘ S), Antarctic convergence zone (roughly 60–50^∘ S), and subtropical convergence zone (roughly 50–40^∘ S) to better account for regional differences in the model biases and obtain better linear fit for the computation of the weights in Eq. (6) (see Fig. S9).

5 Data availability

Data and analysis scripts can be accessed at https://data.giss.nasa.gov/oceans/carbonstates.

6 Conclusions

This proof-of-concept study presents the k-means cluster analysis and the determination of the regimes called “ocean carbon states” in observation-based data of the ocean carbon cycle. A method is described here to determine the optimal number of clusters for the cluster analysis. The study also explores how to characterize the ocean carbon states temporally and spatially in order to determine the physical–biogeochemical processes related to each carbon state. Composites of the CO₂ flux and a quantitative exploration of the effect of each field on pCO_2 sw bias are also demonstrated.

In this study, pCO₂ and SST were chosen as the two variables that co-determine the carbon states, based on the fact that they both play critical roles in the biogeochemistry and the physics of the ocean system and control the flux of CO₂. One may choose different variables and it would be interesting to see whether and how the regimes depend on the choice of variables.

We have also tested the importance of the choice of k. A main caveat of k-means cluster analysis is that k must be predetermined through reasoning that is subject to personal bias. However, we show that by assessing the clusters from multiple angles (i.e., the score plots, the sensitivity criterion visual inspection, analysing cluster outputs with increasing k, temporal attribution), it is possible to determine an optimal k that is semi-objective. Even so, in this proof of concept study, we acknowledge the uncertainty in our choice of k as a result of the small dataset of 12-monthly 2-D histograms, which occasionally results in there being only a small number of histograms per cluster.

The ocean carbon states we obtain from this climatological year dataset are interesting. We found that the subtropical North Atlantic is the dominant feature in the cold season regime (the months January through April). In the same regime, the subpolar North Atlantic also features prominently, which is associated with the high variability in this area due to sea ice retreat, the spring bloom and the winter–spring convection. In contrast, the tropical Atlantic dominates the warm months June through October, while the subtropical and subpolar regions play a smaller role. The transition regime, which is comprised of months that do not entirely fall into the winter or summer regimes, shows again the lower tropics and the subtropical gyre to be more active. We would expect that a longer dataset that includes natural variability as well as the effects of longer-term climate and anthropogenic trends would result in more carbon states and hence that it would be an interesting extension of the present study.

The NASA-GISS model carbon states in the North Atlantic are similar, both in temporal as well as spatial characterization, to the observed ones, with better model skill in the summer than in the winter. Specifically, the model overestimates the importance of the subtropical gyre and underestimates the subpolar gyre during the cold months. During summer, the model underestimates the tropics, but not significantly. The transition months are found to behave differently in the model, although that might be a result of the small size of our input datasets.

In the Southern Ocean, during the warmer months (January–March), the observational states are more persistent along 40^∘ S, the subtropical convergence zone, while the colder season has prominent states (higher persistency) mostly along the Antarctic coast. The transition regime shows a similar degree of variability across the entire Southern Ocean.

While the GISS model agrees in the temporal characterization of the ocean carbon states, it diverges from the observational spatial attribution, particularly in the summer and the transition regimes. It is of note here, however, that the Takahashi climatology is far more uncertain in the Southern Ocean (Takahashi et al., 2009) than it is in the North Atlantic, and therefore the model's lack of skill might not be as alarming. New observations in the area (e.g., from SOCCOM) will greatly benefit studies such as this.

Error analysis of the model response helps explain the GISS model biases. Applying k-means clustering analysis in the two main regions of the world that are known to be critical for the global ocean carbon cycle, namely the North Atlantic region and the Southern Ocean, defines the priorities for model improvement: in the North Atlantic biases in surface salinity, wind speed and surface temperature, whereas in the Southern Ocean priorities are nitrate and surface salinity. Clearly the GISS climate model would benefit from more realistic representation of the nitrogen cycle in the ocean as a whole.

The goal of this study is to enable us to apply this k-means clustering to “big” data, in order to find the interannual and regional patterns in larger, higher frequency climate datasets. This extended application will allow researchers to gain a much more comprehensive insight and intuition for physical systems by mechanistically and impartially grouping multiple variables that form the prominent features of these networks. Other variable pairs besides pCO₂ and SST will also be explored, such as CO₂ flux and chlorophyll, in order to assess other drivers in Eq. (1). Finally, higher order clustering and classification techniques will be analyzed in order to determine the most efficient and successful method for understanding the ocean carbon cycle.

All routines and datasets used in this study are freely available on the Ocean Carbon States page of the NASA Goddard Institute for Space Studies web portal (https://data.giss.nasa.gov/oceans/carbonstates).