The countrywide historical gravity dataset of Lithuanian territory

The historical gravity dataset of Lithuania consists of two files based on measurements carried out between 1951 and 1962: data of second and third order gravimetric network as well as data from gravity surveys. Raw data were collected by digitising the paper catalogues of gravimetric network stations and sheets of gravimetric map at a scale 1:200 000. The gravity data set covers the entire territory of Lithuania (65 000 km²). Raw data were collected by digitising the paper catalogues of gravimetric network stations and sheets of gravimetric map at a scale 1:200 000. Initially the gravity data were in Potsdam gravity system, geodetic coordinates of the gravity points – in the coordinate reference system Pulkovo 1942 (EPSG: 2499), and the heights of gravity points – in the Baltic normal height system of 1977 (EPSG code 5705). In the final countrywide set the gravity data are in the International Gravity Standardization Net of 1971 gravity system, geodetic coordinates – in European Terrestrial Reference System of 1989 coordinate reference system (EPSG:4258), and geodetic heights – in the European Vertical Reference System of 2007 (EPSG:5215). The total number of gravimetric network stations is 123, and the total number of gravity survey points is 10 660. The data were recorded into files applying DBF (Data Base Format) format. The historical gravity data set could be used for quasi-geoid modelling, for development of Earth geopotential models and for geological interpretation. Researchers will benefit in the process of evaluation and accuracy estimation of the developed products using high precision data of gravity network stations. Dataset is available at https://doi.org/10.5281/zenodo.15090241 (Šlikas et al., 2025).

1 Introduction

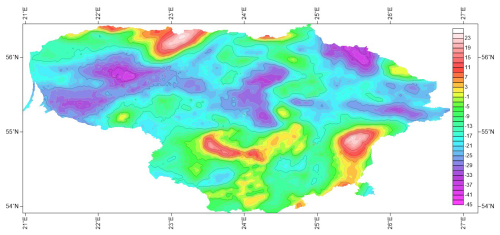
The historical gravity survey of the Earth`s gravity field in Lithuania was carried out in 1951–1962 (Paršeliūnas and Petroškevičius, 2007; Paršeliūnas et al., 2010; Petroškevičius, 2004; Petroškevičius et al., 2014). The data are tied to reference gravity stations in Vilnius, Panevėžys, Rīga, Daugavpils, Lida and Karaliaučius. In total 10 660 gravimetric points were observed (Fig. 1). On the basis of this gravity survey the gravimetric map at a scale 1:200 000 was generated. The gravity data was tied to the Potsdam gravity system, geodetic coordinates of the gravity points are in the coordinate reference system Pulkovo 1942 (EPSG:2499), and the heights of gravity points are in the Baltic normal height system of 1977 (EPSG code 5705). Investigations showed that the average accuracy of the gravity measurements determined from gravimetric map, is about 0.7 mGal (1 mGal = 10⁻⁵ m s⁻²). However, in some areas accuracy is much worse, as much as 3 mGal (Birvydienė, 2010). The gravimetric network of the third order (105 stations) was developed in 1952–1962, and the second order network (18 stations) was developed in 1968 (Paršeliūnas and Petroškevičius, 2007; Petroškevičius, 2004). The overview of historical gravity data set is presented in Fig. 1.

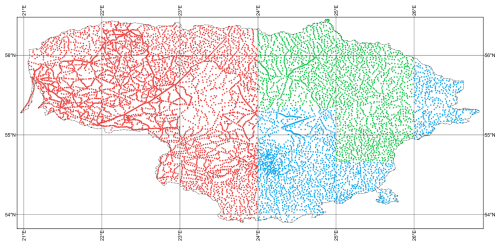
Figure 1 Distribution of the historical gravimetric points in the territory of investigation and compilation. Colours indicate the types of normal heights used in the compilation (see Fig. 5).

These harmonized data provide unprecedented insights into the gravity field of entire country, supporting diverse applications in geodesy, geophysics, geology, and related scientific fields. High-resolution gravity datasets offer critical information for analyzing Earth's gravitational field, refining geopotential models, and constructing precise geoid models. Furthermore, researchers will benefit from using high-precision gravity network points to evaluate and estimate the accuracy of these developed products.

Similar gravity data sets have been compiled in other countries at countrywide (APAT, 2005; Basic and Bjelotomic, 2014; Csapó and Völgyesi, 2002; Martelet et al., 2009; Meurers and Ruess, 2009; Stopar, 2016), regional (Zahorec et al., 2021; Bielik et al., 2006; Denker and Torge, 1998; Denker and Roland, 2005; Ågren et al., 2016) and global scales (Förste et al., 2014; Pavlis et al., 2012).

2 Experimental design, materials and methods

2.1 Historical gravity data sources

The historical gravity data set is based on two gravity data sources:

• Second and third order gravity network stations (18 and 105 gravimetric stations);

• Gravimetric maps at a scale 1:200 000 (10 660 gravimetric points).

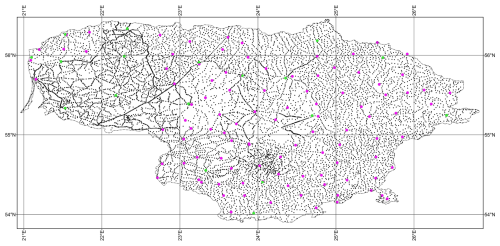
The data of the second and third order gravity network stations were collected by digitising the catalogues of the gravimetric stations. Distribution of the second and third order gravimetric stations in the territory of Lithuania is presented in the Fig. 2.

Figure 2 Distribution of the second and third order gravimetric stations (green dots – second order stations; magenta dots – third order stations).

The gravimetric measurements at second and third order network stations were carried out by relative gravimeters ΓAK-3M, ΓAK-4M, ΓAK-ΠT, ΓAK-7T. The standard deviation of the accelerations due to gravity does not exceed 0.35 mGal (Birvydienė, 2010). The coordinate reference system of Pulkovo 1942 (EPSG code 2499), the Krassowsky ellipsoid of 1940 (EPSG code 7024) and Baltic normal height system of 1977 (EPSG code 5705) were used for positioning of gravimetric points. The accelerations due to gravity were expressed in Potsdam system and utilised the Helmert normal gravity field.

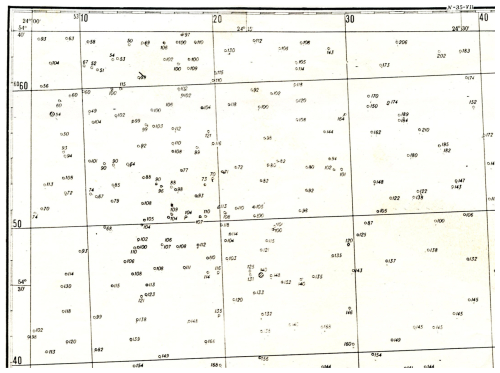
The gravimetric map was based on data from the gravimetric survey carried out in the period from 1951 till 1962 (Birvydienė, 2010). Gravimetric measurements were performed by relative gravimeters CH-3, ΓKA, ΓAK-3M, ΓAK-4M, ΓKM. Normal heights of the gravimetric points were measured by geometric-barometric levelling or estimated from topographic maps at a scale of 1:25 000. The third-class gravimetric network was used as base for the map. The coordinate reference system of Pulkovo 1942 (EPSG code 2499), the Krassowsky ellipsoid of 1940 (EPSG code 7024) and Baltic height system of 1977 (EPSG code 5705) were used for positioning of gravimetric points. The horizontal positions were determined from the topographic maps at a scale 1:25 000, 1:50 000 or even 1:100 000. On the basis of this gravity survey, the gravimetric map at a scale 1:200 000 was constructed applying Gauss–Krüger projection (EPSG code 2499). Examples of the gravimetric maps are presented in the Figs. 3 and 4.

Figure 3 Example of part of Bouguer anomaly map for which normal heights are not available (contour interval is 2 mGal) (The firm, 1965).

Figure 4 Example of a gravimetric map at a scale 1:200 000 containing the free air anomalies (in mGal) of gravimetric points (The firm, 1965). This map covers the same area as the map in Fig. 3.

The Bouguer gravity anomalies due to gravity were written at each point in the map. The total number of gravimetric points is 10 663. The Helmert's formula for the estimation of normal gravity field and the density of the Earth's crust δ=2.3 g cm⁻³ were used for calculations of the anomalies due to gravity. The gravity field is presented by isolines at every 2 mGal. The Bouguer anomalies due to gravity were calculated following Eq. (1) (Torge, 1989):

$$\begin{array}{}\text{(1)}& \mathrm{\Delta }{g}_{\mathrm{P}}^{\mathrm{B}}=g_{\mathrm{P}}-{\mathit{\gamma }}_{\mathrm{H}}^{\mathrm{0}}+\mathrm{0.3086}{H}_{\mathrm{77}}-\mathrm{0.0419}\mathit{\delta }\cdot H_{\mathrm{77}}\end{array}$$

where g_P – Potsdam system gravity acceleration measured at the point on the Earth surface; ${\mathit{\gamma }}_{\mathrm{H}}^{\mathrm{0}}$ – the acceleration of Helmert normal gravity field on equipotential ellipsoid surface, H₇₇ – normal height at point on the Earth's surface in the Baltic Height System of 1977. The accelerations of Helmert's normal gravity field on equipotential ellipsoid surface were obtained following Eq. (2) (Petroškevičius, 2004):

$$\begin{array}{}\text{(2)}& {\mathit{\gamma }}_{\mathrm{H}}^{\mathrm{0}}=\mathrm{978}\mathrm{030}\left(\mathrm{1}+\mathrm{0.005302}{\sin }^{\mathrm{2}}{B}_{\mathrm{42}}-\mathrm{0.000007}{\sin }^{\mathrm{2}}\mathrm{2}{B}_{\mathrm{42}}\right),\end{array}$$

where B₄₂ – the latitude of gravimetric point in Pulkovo 1942 coordinate reference system.

Unfortunately, the number of the map sheets containing normal heights of the gravimetric points was very limited (Fig. 5).

Figure 5 Types of map sheets used to determine the normal heights of the gravimetric points. Patterns indicate the types of map sheets used in the compilation: dots – normal heights interpolated from topographic map; cross-lines – map sheets containing the normal heights; lines – normal heights derived from Bouguer anomalies and free air anomalies.

To determine the normal heights of gravimetric points for the new calculations, two additional approaches were employed:

• Paper map sheets at a scale 1:200 000 with free air anomalies (Fig. 6) that were compared to maps sheets, containing the normal heights of gravimetric points (Fig. 7).

• Paper topographic map sheets at a scale 1:10 000 (Fig. 8).

Figure 6 Example of a map sheet containing the free air anomalies (in mGal) (The firm, 1965).

Figure 7 Example of a map sheet containing the normal heights of gravimetric points, but no gravity values (The firm, 1965). This map covers the same area as the map in Fig. 6.

2.2 Modern compilation of the historical gravity data set

Preparation of a modern, new compilation of the historical gravity data set includes three items:

• Introduction of the European Terrestrial Coordinate System of 1989 (ETRS89).

• Introduction of the European Vertical Reference System of 2007 (EVRS07).

• Introduction of the International Gravity Standardization Net of 1971 gravity system (IGSN71).

2.2.1 Introduction of the coordinate reference system ETRS89

One of the key problems in the unification of gravimetric databases is the homogenization of position, height and gravimetric coordinate systems used in each database. Through its historical development, each country has used and sometimes still uses local systems and their realisation, which are often based on reference systems that are tied to older ellipsoids or older geodetic reference networks and projections. These systems and their realisations thus contain several differences, which are responsible for large inhomogeneities, shifts, errors in position, height, and gravity. These errors are most evident in the mutual comparison of data from individual countries or when modern surveys are incorporated with older data.

To avoid these problems in the position of gravimetric points, all position data were transformed from local systems to the global system, i.e., the European Terrestrial Reference System 1989, which is accurate, homogeneous, and recommended for all European countries (Altamimi and Collilieux, 2024). A similar situation is in the height systems where countries use different types of physical heights, that are linked to different tide gauges and each country has a different practical implementation of the relevant height system (EVRS, 2020). The solution is again transformation to a uniform platform in the form of ellipsoidal heights in the ETRS89 system based on the ellipsoid GRS80 (Moritz, 1984, 2000).

The situation is similar in gravimetric reference systems, where especially the gravimetric databases that have been created for decades often use old gravimetric systems connected to the 1909 Potsdam system. An important step was therefore to convert these data into gravimetric systems, which are connected to absolute gravimetric points and measurements, such as IGSN71 (Morelli et al., 1974) or modern national systems connected with the recent absolute measurements, which are verified by international comparisons of absolute gravimeters (Francis et al., 2015).

The Coordinate Reference System of gravimetric points both from the historical catalogues and from gravimetric maps was Pulkovo 1942 system (EPSG code: 2499). To express the geodetic coordinates of the points in modern European Terrestrial Reference System of 1989 (ETRS89, EPSG code: 4258) the three steps algorithm was employed. In the first step the geocentric coordinates of the gravimetric points were calculated from the geodetic ellipsoidal coordinates expressed in Pulkovo 1942 system applying formulas from (Schödlbauer, 1981, 1982; Annoni et al., 2001) (see Algorithm A1 in Appendix).

In the second step the geocentric coordinates of the gravimetric points expressed in Pulkovo 1942 system were transformed to ETRS89 geocentric coordinates by applying standard Helmert's seven parameters transformation formula (Reit, 2010) (see Algorithm A2 in Appendix). Values of the transformation parameters between Pulkovo 1942 and ETRS89 systems were derived by analysing the geocentric coordinates of 45 geodetic points, evenly distributed across Lithuania (Fig. 9).

In the third step the ETRS89 ellipsoidal coordinates were calculated from the ETRS89 geocentric coordinates applying formulas from (Schödlbauer, 1981, 1982; Annoni et al., 2001) (see Algorithm A3 in Appendix).

2.2.2 Introduction the European vertical reference system EVRS07

EVRS07 (EPSG: 5215) is realized by geopotential numbers and normal heights of the United European Levelling Network (UELN) (Sacher et al., 2008; Ihde et al., 2008; Dragomir et al., 2011). The newest realisation of EVRS is EVRF2019 (EPSG: 1274). EVRF2019 is a zero-tide surface (Sacher and Liebsch, 2019). It should be noted, that the difference between the realisations in Lithuania is about 1 cm only and for calculations of historical gravity data set is negligible. Federal Agency for Cartography and Geodesy (BKG – Bundesamt fűr Kartographie und Geodesie), Germany, and the Reference Frame Sub-Commission for Europe (EUREF) have developed a formulae for transformation between the local height (vertical) systems and European Vertical Reference System of 2007 (Celms et al., 2014; Kadaj, 2018; Dragomir et al., 2011). In the historical gravity data set the normal heights of gravity points were expressed in Baltic Heights System of 1977 referred to tide gauge Kronstadt (BHS77) (see Algorithm A4 in Appendix). Distribution of the common points used for calculation of the transformation parameters is shown in Fig. 10.

In total there are 233 height benchmarks in Lithuania for which normal heights could be found in both height systems.

2.2.3 Introduction of the Gravity system IGSN71

IGSN71 is used here to harmonize legacy gravity data. In fact, IGSN71 is no longer considered the most accurate or modern reference for gravity data, so future work should integrate absolute gravity stations in the European Absolute Gravity Reference Network, and transformation offsets to newer national absolute reference values should be computed and documented. However, here the values of accelerations due to gravity g_p, digitised from catalogues and referred to the Potsdam gravity system were recalculated to the IGSN71 system (g₇₁) by simple subtraction of 14.0 mGal as the difference between the two gravity systems (Wollard, 1979; Torge, 1989; Petroskevicius, 2004) (see Algorithm A5 in Appendix). Figure 11 shows the spatial distribution of gravimetric points of all countrywide historical gravity data set, and Bouguer anomaly map is presented in Fig. 12.

3 Data availability

The historical gravity data set is available in the ZENODO repository at https://doi.org/10.5281/zenodo.15090241 (Šlikas et al., 2025). The data were recorded into files in the DBF (Data Base Format) format (Digital, 2012). The database structure is presented in Table 1.

Table 1 The database structure of the historical gravity data set.

4 Conclusions

In this study, the countrywide historical gravity data set was recompiled. It consists of two database files: data of gravity network points (123 stations) and data of gravity survey (10 660 points). The estimated accuracy of gravity network stations is about 0.2 mGal (second order stations) and 0.35 mGal (third order stations), and accuracy of the gravity survey points is about 0.7 mGal.

The transformation parameters and algorithms to introduce the European Terrestrial Coordinate System of 1989 (ETRS89), European Vertical Reference System of 2007 (EVRS07) and International Gravity Standardization Net of 1971 gravity system (IGSN71) were defined.

These data are useful in understanding the gravity field of Lithuania and could be used for quasi-geoid modelling, creating the geopotential models and for geological interpretation. Researchers will benefit during evaluation and accuracy estimation of developed products using high precision data of gravity network points.

Figure 8 Example of a topographic map sheet at a scale 1:10 000 (Topographic map, 1958).

Figure 9 Distribution of geodetic points used for the transformation parameters calculation.

Figure 10 Distribution of the common points used for calculation of the transformation parameters for the conversion of heights between elevation datums (233 points).

Figure 11 Spatial distribution of gravimetric points of the entire historical gravity data set (green dots – second order stations; magenta dots – third order stations; black dots – gravity survey points).

Figure 12 Bouguer anomaly map (contour interval is 2 mGal).

Appendix A

Algorithm A1. Convertion the ellipsoidal coordinates to the rectangular geocentric coordinates.

• Input.: the ellipsoidal coordinates: geodetic latitude B₄₂, geodetic longitude L₄₂, ellipsoidal height $H_{\mathrm{e}}^{\mathrm{K}}$ and parameters of ellipsoid a and f (in our case – Krassowsky 1940 ellipsoid: a=6 378 245 m, f=298.3).

• Output: the rectangular geocentric coordinates $X_{\mathrm{42}}^{\prime }$, $Y_{\mathrm{42}}^{\prime }$, $Z_{\mathrm{42}}^{\prime }$.

Calculation formulaes (CRS-Geo, 2025):

$$\begin{array}{}\text{(A1)}& {\displaystyle }& {\displaystyle }{X}_{\mathrm{42}}^{\prime }=\left(N_{\mathrm{K}}+H_{\mathrm{e}}^{\mathrm{K}}\right)\cos B_{\mathrm{42}}\cos L_{\mathrm{42}},\text{(A2)}& {\displaystyle }& {\displaystyle }{Y}_{\mathrm{42}}^{\prime }=\left(N_{\mathrm{K}}+H_{\mathrm{e}}^{\mathrm{K}}\right)\cos B_{\mathrm{42}}\sin L_{\mathrm{42}},\text{(A3)}& {\displaystyle }& {\displaystyle }{Z}_{\mathrm{42}}^{\prime }=\left(N_{\mathrm{K}}+H_{\mathrm{e}}^{\mathrm{K}}-N_{\mathrm{K}}{e}^{\mathrm{2}}\right)\sin B_{\mathrm{42}},\end{array}$$

here

$$\begin{array}{}\text{(A4)}& {\displaystyle }& {\displaystyle }{N}_{\mathrm{K}}={\displaystyle \frac{a}{\sqrt{\mathrm{1}-e^{\mathrm{2}}{\sin }^{\mathrm{2}}{B}_{\mathrm{42}}}}},\text{(A5)}& {\displaystyle }& {\displaystyle }{e}^{\mathrm{2}}=\mathrm{2}\cdot f-f^{\mathrm{2}}.\end{array}$$

Example. The Pulkovo 1942 (Krassowsky 1940 ellipsoid) ellipsoidal coordinates of gravimetric point are: B₄₂=55°15^′22.9^′′, L₄₂=23°52^′26.1^′′, $H_{\mathrm{e}}^{\mathrm{K}}=\mathrm{22.4}$ m. Calculated rectangular geocentric coordinates are:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{X}_{\mathrm{42}}^{\prime }=\mathrm{3}\mathrm{331}\mathrm{529.1}\mathrm{m},Y_{\mathrm{42}}^{\prime }=\mathrm{1}\mathrm{474}\mathrm{516.4}\mathrm{m},\\ {\displaystyle }& {\displaystyle }{Z}_{\mathrm{42}}^{\prime }=\mathrm{5}\mathrm{217}\mathrm{810.9}\mathrm{m}.\end{array}$$

Algorithm A2. Calculation the transformation parameters between Pulkovo 1942 and ETRS89 CRS,

• Input: the rectangular geocentric coordinates $X_{\mathrm{42}}^{\prime }$, $Y_{\mathrm{42}}^{\prime }$, $Z_{\mathrm{42}}^{\prime }$ in Pulkovo 1942 CRS.

• Output: the rectangular geocentric coordinates X₈₉, Y₈₉, Z₈₉ in ETRS89 CRS.

Calculation formulaes (Reit, 2010):

$$\begin{array}{}\text{(A6)}& \left(\begin{array}{c}{X}_{\mathrm{89}}\\ Y_{\mathrm{89}}\\ Z_{\mathrm{89}}\end{array}\right)=\left(\begin{array}{c}\mathit{\delta }x\\ \mathit{\delta }y\\ \mathit{\delta }z\end{array}\right)+R\left(\begin{array}{c}{X}_{\mathrm{42}}^{\prime }\\ Y_{\mathrm{42}}^{\prime }\\ Z_{\mathrm{42}}^{\prime }\end{array}\right)(\mathrm{1}+\mathit{\delta }m),\end{array}$$

where X₈₉, Y₈₉, Z₈₉ – rectangular geocentric coordinates of the points in ETRS89 system, $X_{\mathrm{42}}^{\prime }$, $Y_{\mathrm{42}}^{\prime }$, $Z_{\mathrm{42}}^{\prime }$ – rectangular geocentric coordinates of the same points in Pulkovo 1942 system, R – matrix of rotations:

$$\begin{array}{}\text{(A7)}& \mathbf{R}=\left(\begin{array}{lll}\mathrm{1}& +{\mathit{\omega }}_z& -{\mathit{\omega }}_y\\ -{\mathit{\omega }}_z& \mathrm{1}& +{\mathit{\omega }}_x\\ +{\mathit{\omega }}_y& -{\mathit{\omega }}_x& \mathrm{1}\end{array}\right).\end{array}$$

Values of the transformation parameters applied to geodetic coordinates of the gravimetric points in the gravity data set:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }\mathit{\delta }x=-\mathrm{40.5953}\mathrm{m};\\ {\displaystyle }& {\displaystyle }\mathit{\delta }y=-\mathrm{18.5498}\mathrm{m};\\ {\displaystyle }& {\displaystyle }\mathit{\delta }z=-\mathrm{69.3396}\mathrm{m};\\ {\displaystyle }& {\displaystyle }{\mathit{\omega }}_x=-\mathrm{0.0000121590}\mathrm{rad};\\ {\displaystyle }& {\displaystyle }{\mathit{\omega }}_y=-\mathrm{0.0000088812}\mathrm{rad};\\ {\displaystyle }& {\displaystyle }{\mathit{\omega }}_z=+\mathrm{0.0000126606}\mathrm{rad};\\ {\displaystyle }& {\displaystyle }\mathit{\delta }m=-\mathrm{0.0000042991}.\end{array}$$

Example. Input: geocentric coordinates in Pulkovo 1942 CRS:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{X}_{\mathrm{42}}^{\prime }=\mathrm{3}\mathrm{331}\mathrm{529.1}\mathrm{m},Y_{\mathrm{42}}^{\prime }=\mathrm{1}\mathrm{474}\mathrm{516.4}\mathrm{m},\\ {\displaystyle }& {\displaystyle }{Z}_{\mathrm{42}}^{\prime }=\mathrm{5}\mathrm{217}\mathrm{810.9}\mathrm{m}.\end{array}$$

Output: geocentric coordinates in ETRS89 CRS:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{X}_{\mathrm{89}}=\mathrm{3}\mathrm{331}\mathrm{567.8}\mathrm{m},Y_{\mathrm{89}}=\mathrm{1}\mathrm{474}\mathrm{398.6}\mathrm{m},\\ {\displaystyle }& {\displaystyle }{Z}_{\mathrm{89}}=\mathrm{5}\mathrm{217}\mathrm{752.3}\mathrm{m}.\end{array}$$

Algorithm A3. Convertion the rectangular geocentric coordinates to the ellipsoidal coordinates.

• Input: the rectangular geocentric coordinates X₈₉, Y₈₉, Z₈₉ and parameters of ellipsoid a and f (in our case parameters of GRS80 ellipsoid, a=6 378 137 m, f=298.257222101 (Moritz, 1984, 2000).

• Output: the ellipsoidal coordinates: geodetic latitude B₈₉, geodetic longitude L₈₉ and ellipsoidal height $H_{\mathrm{e}}^{\mathrm{80}}$.

Calculation formulaes:

$$\begin{array}{}\text{(A8)}& L_{\mathrm{89}}=\mathrm{arctg}\left(Y_{\mathrm{89}}/X_{\mathrm{89}}\right);\end{array}$$

Initial geodetic latitude:

$$\begin{array}{}\text{(A9)}& B_{\mathrm{0}}=\mathrm{arctg}\left(Z_{\mathrm{89}}/{\left(\left(\mathrm{1}-e_{\mathrm{80}}^{\mathrm{2}}\right)\left(X_{\mathrm{89}}^{\mathrm{2}}+Y_{\mathrm{89}}^{\mathrm{2}}\right)\right)}^{\mathrm{1}/\mathrm{2}}\right);\end{array}$$

here

$$\begin{array}{}\text{(A10)}& e_{\mathrm{80}}^{\mathrm{2}}=\mathrm{2}\cdot f-f^{\mathrm{2}}.\end{array}$$

Iterations till $B_i-B_{i-\mathrm{1}}>\mathrm{\Delta }$, where Δ is an appropriately chosen value defining the necessary precision of latitude B (in our case $\mathrm{\Delta }={\mathrm{0.1}}^{\prime \prime }$):

$$\begin{array}{}\text{(A11)}& {\displaystyle }& {\displaystyle }{N}_i={\displaystyle \frac{a}{\sqrt{\mathrm{1}-e_{\mathrm{80}}^{\mathrm{2}}{\sin }^{\mathrm{2}}{B}_{i-\mathrm{1}}}}};\text{(A12)}& {\displaystyle }& {\displaystyle }{H}_i^{\mathrm{e}}={\displaystyle \frac{Z}{\sin B_{i-\mathrm{1}}}}-\left(\mathrm{1}-e_{\mathrm{80}}^{\mathrm{2}}\right)N_i,\end{array}$$

$$\begin{array}{}\text{(A13)}& B_i=\mathrm{arctg}\left({\displaystyle \frac{Z_{\mathrm{89}}}{{\left(X_{\mathrm{89}}^{\mathrm{2}}+Y_{\mathrm{89}}^{\mathrm{2}}\right)}^{\mathrm{1}/\mathrm{2}}}}\cdot {\displaystyle \frac{\mathrm{1}}{\mathrm{1}-\left(e_{\mathrm{80}}^{\mathrm{2}}{N}_i\right)/\left(N_i+H_i^{\mathrm{e}}\right)}}\right).\end{array}$$

Example. The rectangular geocentric coordinates of gravimetric point are:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{X}_{\mathrm{89}}=\mathrm{3}\mathrm{331}\mathrm{567.8}\mathrm{m},Y_{\mathrm{89}}=\mathrm{1}\mathrm{474}\mathrm{398.6}\mathrm{m},\\ {\displaystyle }& {\displaystyle }{Z}_{\mathrm{89}}=\mathrm{5}\mathrm{217}\mathrm{752.3}\mathrm{m}.\end{array}$$

Calculated ETRS89 (GRS80 ellipsoid) ellipsoidal coordinates are:

$$B_{\mathrm{89}}=\mathrm{55}\mathit{°}{\mathrm{15}}^{\prime }{\mathrm{22.2}}^{\prime \prime },L_{\mathrm{89}}=\mathrm{23}\mathit{°}{\mathrm{52}}^{\prime }{\mathrm{19.1}}^{\prime \prime }{H}_{\mathrm{e}}^{\mathrm{80}}=\mathrm{77.1}\mathrm{m}.$$

Algorithm A4. Calculation the transformation parameters between BHS77 and EVRS07 height systems.

Formulae to transform BHS77 normal height to EVRS07 normal height is as follow Eq. (A14):

$$\begin{array}{}\text{(A14)}& \begin{array}{rl}{H}_{\mathrm{07}}& =H_{\mathrm{77}}+{\mathit{\alpha }}_{\mathrm{1}}+{\mathit{\alpha }}_{\mathrm{2}}{M}_{\mathrm{0}}\left(B_{\mathrm{89}}-B_{\mathrm{0}}\right)\\ & +{\mathit{\alpha }}_{\mathrm{3}}{N}_{\mathrm{0}}\left(L_{\mathrm{89}}-L_{\mathrm{0}}\right)\cos B_{\mathrm{89}},\end{array}\end{array}$$

here

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{H}_{\mathrm{07}}\text{–}\mathrm{normal}\mathrm{height}\mathrm{referred}\mathrm{to}\mathrm{EVRS}\mathrm{07}\mathrm{vertical}\mathrm{system};\\ {\displaystyle }& {\displaystyle }{H}_{\mathrm{77}}\text{–}\mathrm{normal}\mathrm{height}\mathrm{referred}\mathrm{to}\mathrm{BAS}\mathrm{77}\mathrm{height}\mathrm{system};\\ {\displaystyle }& {\displaystyle }{P}_{\mathrm{0}}\left(B_{\mathrm{0}},L_{\mathrm{0}}\right)\text{–}\mathrm{origin}\mathrm{for}\mathrm{the}\mathrm{height}\mathrm{transformation}\mathrm{in}\\ {\displaystyle }& {\displaystyle }\mathrm{Lithuania}\mathrm{with}\mathrm{geodetic}\mathrm{latitude}\mathrm{and}\mathrm{longitude}\mathrm{in}\mathrm{ETRS}\mathrm{89}\\ {\displaystyle }& {\displaystyle }\mathrm{CRS};\\ {\displaystyle }& {\displaystyle }{M}_{\mathrm{0}}\text{–}\mathrm{radius}\mathrm{of}\mathrm{curvature}\mathrm{in}\mathrm{the}\mathrm{meridian}\mathrm{at}\mathrm{the}\mathrm{point}{P}_{\mathrm{0}};\\ {\displaystyle }& {\displaystyle }{N}_{\mathrm{0}}\text{–}\mathrm{radius}\mathrm{of}\mathrm{curvature}\mathrm{of}\mathrm{the}\mathrm{prime}\mathrm{vertical}\mathrm{at}\mathrm{the}\mathrm{point}{P}_{\mathrm{0}};\\ {\displaystyle }& {\displaystyle }{\mathit{\alpha }}_{\mathrm{1}}\text{–}\mathrm{coefficient}\mathrm{of}\mathrm{the}\mathrm{displacement}\mathrm{in}\mathrm{vertical}\mathrm{direction};\\ {\displaystyle }& {\displaystyle }{\mathit{\alpha }}_{\mathrm{2}}\text{–}\mathrm{coefficient}\mathrm{of}\mathrm{the}\mathrm{slope}\mathrm{along}\mathrm{meridian};\\ {\displaystyle }& {\displaystyle }{\mathit{\alpha }}_{\mathrm{3}}\text{–}\mathrm{coefficient}\mathrm{of}\mathrm{the}\mathrm{slope}\mathrm{along}\mathrm{prime}\mathrm{vertical};\\ {\displaystyle }& {\displaystyle }{B}_{\mathrm{89}}\text{–}\mathrm{latitude}\mathrm{of}\mathrm{the}\mathrm{point}\mathrm{to}\mathrm{transform};\\ {\displaystyle }& {\displaystyle }{L}_{\mathrm{89}}\text{–}\mathrm{longitude}\mathrm{of}\mathrm{the}\mathrm{point}\mathrm{to}\mathrm{transform}.\end{array}$$

The formulas for M₀ and N₀ can be found in number of sources, for example (Tobler, 1964; Lenart, 2013, 2017):

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{N}_{\mathrm{0}}={\displaystyle \frac{a}{\sqrt{\left(\mathrm{1}-e_{\mathrm{80}}^{\mathrm{2}}{\sin }^{\mathrm{2}}{B}_{\mathrm{0}}\right)}}};\\ {\displaystyle }& {\displaystyle }{M}_{\mathrm{0}}={\displaystyle \frac{a\left(\mathrm{1}-e_{\mathrm{80}}^{\mathrm{2}}\right)}{{\left(\mathrm{1}-e_{\mathrm{80}}^{\mathrm{2}}{\sin }^{\mathrm{2}}{B}_{\mathrm{0}}\right)}^{\mathrm{3}/\mathrm{2}}}}={\displaystyle \frac{N_{\mathrm{0}}\left(\mathrm{1}-e_{\mathrm{80}}^{\mathrm{2}}\right)}{\mathrm{1}-e_{\mathrm{80}}^{\mathrm{2}}si{n}^{\mathrm{2}}{B}_{\mathrm{0}}}}\end{array}$$

where a – semimajor axis and $e_{\mathrm{80}}^{\mathrm{2}}$ – squared first eccentricity of GRS80 ellipsoid (Eq. A10).

Parameters of transformation between BHS77 and EVRS07 were calculated as follow:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{B}_{\mathrm{0}}=\mathrm{55}\mathit{°}{\mathrm{18}}^{\prime };L_{\mathrm{0}}=\mathrm{24}\mathit{°}{\mathrm{01}}^{\prime };{\mathit{\alpha }}_{\mathrm{1}}=\mathrm{0.1425}\mathrm{m};\\ {\displaystyle }& {\displaystyle }{\mathit{\alpha }}_{\mathrm{2}}={\mathrm{0.06076}}^{\prime \prime };{\mathit{\alpha }}_{\mathrm{3}}={\mathrm{0.03375}}^{\prime \prime }.\end{array}$$

The minimum value of residuals equal to −0.025 m and maximum value equal to +0.024 m were obtained. The standard deviation of transformation equal to 0.013 m was derived.

Example:

$$\begin{array}{ll}{\displaystyle }& {\displaystyle }{B}_{\mathrm{89}}=\mathrm{55}\mathit{°}{\mathrm{42}}^{\prime };L_{\mathrm{89}}=\mathrm{24}\mathit{°}{\mathrm{21}}^{\prime };H_{\mathrm{77}}=\mathrm{55.90}\mathrm{m};\\ {\displaystyle }& {\displaystyle }{H}_{\mathrm{07}}=\mathrm{56.06}\mathrm{m}.\end{array}$$

Algorithm A5. Calculation the gravity values tied to the Potsdam gravity system to the IGSN71 system.

The values of accelerations due to gravity g_p referred to the Potsdam gravity system were calculated to the IGSN71 system g₇₁ by simple subtraction of 14.0 mGal as the difference between the two gravity systems:

$$\begin{array}{}\text{(A15)}& g_{\mathrm{71}}=g_{\mathrm{p}}-\mathrm{14.0}.\end{array}$$

The free air anomalies due to gravity were calculated following Eq. (A16):

$$\begin{array}{}\text{(A16)}& \mathrm{\Delta }{g}_{\mathrm{71}}^{\mathrm{F}}=g_{\mathrm{71}}-{\mathit{\gamma }}_{\mathrm{80}}^{\mathrm{0}}-\mathrm{\Delta }\mathit{\gamma },\end{array}$$

here ${\mathit{\gamma }}_{\mathrm{80}}^{\mathrm{0}}$ – the accelerations of GRS80 normal gravity field on equipotential ellipsoid surface:

$$\begin{array}{}\text{(A17)}& {\mathit{\gamma }}_{\mathrm{80}}^{\mathrm{0}}={\mathit{\gamma }}_{\mathrm{80}\mathrm{e}}^{\mathrm{0}}{\displaystyle \frac{\mathrm{1}+k_{\mathrm{80}}{\sin }^{\mathrm{2}}{B}_{\mathrm{89}}}{\sqrt{\mathrm{1}-e_{\mathrm{80}}^{\mathrm{2}}{\sin }^{\mathrm{2}}{B}_{\mathrm{89}}}}},\end{array}$$

here ${\mathit{\gamma }}_{\mathrm{80}\mathrm{e}}^{\mathrm{0}}$, e₈₀, k₈₀ – parameters of GRS80 normal gravity field (Moritz, 2000); ${\mathit{\gamma }}_{\mathrm{80}\mathrm{e}}^{\mathrm{0}}=\mathrm{978}\mathrm{032.67715}$ mGal; $e_{\mathrm{80}}^{\mathrm{2}}=\mathrm{0.00669438002290}$; k=0.001931851353; B₈₉ – latitude of gravimetric point in ETRS89 system.

Corrections due to normal heights H₀₇ , i.e. free-air corrections, were calculated following Eq. (A18):

$$\begin{array}{}\text{(A18)}& \mathrm{\Delta }\mathit{\gamma }=-\mathrm{0.30855}\left(\mathrm{1}+\mathrm{0.00071}\cos \left(\mathrm{2}{B}_{\mathrm{89}}\right)\right)H_{\mathrm{07}}.\end{array}$$

Standard deviations of free air gravity anomalies were calculated following Eq. (A19):

$$\begin{array}{}\text{(A19)}& m_{\mathrm{l}}=\sqrt{m_{\mathrm{g}}^{\mathrm{2}}+m_{{\mathit{\gamma }}^{\mathrm{0}}}^{\mathrm{2}}+m_{\mathrm{\Delta }\mathit{\gamma }}^{\mathrm{2}}},\end{array}$$

where m_g – standard deviation of measured gravity acceleration (from the catalogue), $m_{{\mathit{\gamma }}^{\mathrm{0}}}$ – standard deviation of normal gravity acceleration ($m_{{\mathit{\gamma }}^{\mathrm{0}}}=\mathrm{1.4}{m}_{\mathrm{B}}^{\prime }$ $m_B^{\prime }$ – standard deviation of geodetic latitude in minutes), m_Δγ – standard deviation of free air reduction (m_Δγ=0.30855 m_H, m_H – standard deviation of normal height in meters).

Bouguer anomalies due to gravity were calculated following Eq. (A20):

$$\begin{array}{}\text{(A20)}& {\left(\mathrm{\Delta }{g}_{\mathrm{71}}^{\mathrm{B}}\right)}_{\mathrm{2.67}}=\mathrm{\Delta }{g}_{\mathrm{71}}^{\mathrm{F}}-\mathrm{\Delta }{g}_{\mathrm{2.67}},\end{array}$$

where correction for an infinite Bouguer slab was calculated following Eq. (A21):

$$\begin{array}{}\text{(A21)}& \mathrm{\Delta }{g}_{\mathrm{2.67}}=-\mathrm{2}\mathit{\pi }\cdot G\cdot \mathit{\delta }\cdot H_{\mathrm{07}},\end{array}$$

where Newtonian gravitational constant $G=\mathrm{6.6743}\times {\mathrm{10}}^{-\mathrm{8}}$ cm³ g⁻¹ s⁻², density of the Earth's crust δ=2.67 g cm⁻³.

Example: g_p=981 552.8 mGal; H₀₇=125.0 m; $B_{\mathrm{89}}=\mathrm{55}\mathit{°}{\mathrm{59.3}}^{\prime }$; g₇₁=981 538.8 mGal; $\mathrm{\Delta }{g}_{\mathrm{71}}^{\mathrm{F}}=-\mathrm{13.67}$ mGal; $(\mathrm{\Delta }{g}_{\mathrm{71}}^{\mathrm{B}}{)}_{\mathrm{2.67}}=-\mathrm{27.67}$ mGal; $m_{\mathrm{B}}={\mathrm{0.1}}^{\prime }$; m_H=0.5 m; m_l=0.7 mGal.

In the case of values taken from the gravimetric maps the values of accelerations due to gravity in IGSN71 system were calculated following Eq. (A22):

$$\begin{array}{}\text{(A22)}& g_{\mathrm{71}}={\left(\mathrm{\Delta }{g}_{\mathrm{P}}^{\mathrm{B}}\right)}_{\mathrm{2.3}}+{\mathit{\gamma }}_{\mathrm{H}}^{\mathrm{0}}-\mathrm{\Delta }\mathit{\gamma }-\mathrm{\Delta }{g}_{\mathrm{2.3}}-\mathrm{14.0},\end{array}$$

where $(\mathrm{\Delta }{g}_{\mathrm{P}}^{\mathrm{B}}{)}_{\mathrm{2.3}}$ – Bouguer anomalies due to gravity digitised from gravimetric map sheets and referred to the Potsdam gravity system, ${\mathit{\gamma }}_{\mathrm{H}}^{\mathrm{0}}$ – normal gravity value, Δγ – correction due normal height (Eq. A18), Δg_2.3 – correction for an infinite Bouguer slab:

$$\begin{array}{}\text{(A23)}& {\displaystyle }\begin{array}{rl}{\mathit{\gamma }}_{\mathrm{H}}^{\mathrm{0}}& =\mathrm{978}\mathrm{030}\cdot \left(\mathrm{1}+\mathrm{0.005302}{\sin }^{\mathrm{2}}{B}_{\mathrm{89}}\right.\\ & \left.-\mathrm{0.0000070}{\sin }^{\mathrm{2}}\left(\mathrm{2}{B}_{\mathrm{89}}\right)\right),\end{array}\text{(A24)}& {\displaystyle }\mathrm{\Delta }{g}_{\mathrm{2.3}}=-\mathrm{0.0419277}\cdot \mathit{\delta }\cdot H_{\mathrm{07}}\end{array}$$

where density of the Earth's crust δ=2.3 g cm⁻³.

In case when the normal heights of the gravimetric points are unknown, the normal heights in BHS77 system were calculated from values of free air anomalies and Bouguer anomalies following Eq. (A25):

$$\begin{array}{}\text{(A25)}& H_{\mathrm{77}}=\left[\mathrm{\Delta }{g}_{\mathrm{P}}^{\mathrm{F}}-{\left(\mathrm{\Delta }{g}_{\mathrm{P}}^{\mathrm{B}}\right)}_{\mathrm{2.3}}\right]/\mathrm{0.09637}\end{array}$$

here $\mathrm{\Delta }{g}_{\mathrm{P}}^{\mathrm{F}}$ – free air anomaly (from gravimetric map of free air gravity anomalies), $(\mathrm{\Delta }{g}_{\mathrm{P}}^{\mathrm{B}}{)}_{\mathrm{2.3}}$ – Bouguer anomaly due to gravity (from gravimetric map of Bouguer anomalies).

Example: $\mathrm{\Delta }{g}_{\mathrm{P}}^{\mathrm{F}}=\mathrm{4.1}$ mGal; $(\mathrm{\Delta }{g}_{\mathrm{P}}^{\mathrm{B}}{)}_{\mathrm{2.3}}=\mathrm{3.1}$ mGal; H₇₇=10.4 m.

Further, the free air and Bouguer anomalies were calculated following Eqs. (A16) and (A20).

Example: $B_{\mathrm{89}}=\mathrm{55}\mathit{°}{\mathrm{59.1}}^{\prime }$; H₀₇=10.4 m; $(\mathrm{\Delta }{g}_{\mathrm{P}}^{\mathrm{B}}{)}_{\mathrm{2.3}}=\mathrm{3.1}$ mGal; $\mathrm{\Delta }{g}_{\mathrm{71}}^{\mathrm{F}}=-\mathrm{13.8}$ mGal; $(\mathrm{\Delta }{g}_{\mathrm{71}}^{\mathrm{B}}{)}_{\mathrm{2.67}}=-\mathrm{14.99}$ mGal; m_Bg=0.7 mGal; m_H=0.5 m; m_l=0.7 mGal.