Data for modern soil chronometry using fallout radionuclides

We describe environmental gamma spectrometry data for >700 soil samples collected from >35 high-resolution quantitative soil profiles spanning global sites. The data are collected for the purpose of modern soil chronometry based on fallout radionuclides (FRNs) ⁷Be and ²¹⁰Pb, using the Linked Radionuclide Accumulation model (LRC). Cumulative gamma counting time for samples in the database exceeds 6.5 years. This is a living database to be augmented as data become available and corrected with improvements in data reduction, or identification of errors. Versions and changes will be indexed. Special attention is paid to measurement uncertainties in the dataset, and to how atmospheric or excess ²¹⁰Pb is defined in both geochemical and mathematical terms for use in the LRC model. Basic familiarity with gamma spectrometry and radionuclide decay chains is assumed. The data set can be accessed at https://doi.org/10.17632/cfxkpn6hj9.1 (Landis, 2025).

1 Introduction

We describe high-precision measurements of environmental radionuclides collected for the purpose of developing modern soil chronometry. Numerous problems such as atmospheric pollutant deposition and carbon sequestration require knowledge of the rates of soil processes that influence metals and carbon through time, but an appropriate chronometry system spanning years to centuries of environmental change has not been available until recent efforts to validate fallout radionuclide (FRN) chronometry (Landis, 2023; Landis et al., 2016, 2024a, b, c). Historically, the impediment to adoption of FRNs in soil systems has been the availability of sufficient instrumental resources to provide long counting times that are necessary for measurement of short-lived ⁷Be, in datasets large enough to develop appropriate age models (Kaste et al., 2011). Here, we report the fallout radionuclides ⁷Be and ²¹⁰Pb, together with bomb pulse ²⁴¹Am and ¹³⁷Cs, and ancillary radiogenic isotopes including ²²⁶Ra, ²²⁸Th, ²²⁸Ra, and others, that are used to construct and verify the Linked Radionuclide Accumulation model (LRC). These radionuclides are all measured concurrently by gamma spectrometry in the Fallout Radionuclide Analytics facility (FRNA) at Dartmouth College. The data are accessible at https://doi.org/10.17632/cfxkpn6hj9.1 (Landis, 2025).

LRC is an empirical age model that dates soil organic and mineral matter based on a mass balance comparison between the soil accumulative ⁷Be : ²¹⁰Pb ratio (R_acc) and the ⁷Be : ²¹⁰Pb atmospheric flux ratio (R_D) (Landis et al., 2016). The data presented currently include more than 700 samples from over 35 high-resolution quantitative soil pits collected using field methods adapted for this purpose, and more are being added each month (Fig. 1). The method is confirmed by accurately dating the bomb-pulse peak in ²⁴¹Am (or ¹³⁷Cs where appropriate) which is known to have occurred in 1963–1964 (Health and Safety Laboratory, 1977). The method is further corroborated by both novel ²²⁸Th : ²²⁸Ra chronometry and ¹⁴C approaches and yields uncertainties on the order of 10 % up to 100 years and 20 % up to 200 years (Landis, 2023; Landis et al., 2024a).

Figure 1 Site map for soils collected for modern soil chronometry.

The majority of sampled soils are what we refer to as “reference”, selected to minimize the potential for historical disturbance through development, land use, natural erosion or tree throw over the past 150 years or more. Additional sites may include experimental designs examining hillslope and alluvial or fluvial processes and should not be taken as representative of reference conditions, i.e. with an expectation that the nuclear bomb-pulse can be accurately dated. Implementation of the LRC model is described elsewhere (Landis et al., 2016). Additional details and challenges of environmental gamma spectrometry (Cutshall et al., 1983; Landis et al., 2012; Murray et al., 1987, 2018) or theories of related FRN age models can also be found elsewhere (Arias-Ortiz et al., 2018; Barsanti et al., 2020; Sanchez-Cabeza and Ruiz-Fernández, 2012). Any brief discussion of these topics here is intended only to contextualize the data and thereby provide an entry point for non-specialist readers. A basic understanding of gamma spectrometry and radionuclide decay chains is assumed.

Finally, data validation is discussed with respect to both analytical problems such as instrument calibration, as well as geochemical problems, namely the susceptibility of Rn to diffuse out of samples in the laboratory as well as from soils in situ. A priority of this manuscript is to demonstrate that routine environmental gamma spectrometry is capable percent-level precision that is expected from other capital analytical platforms such as inductively-coupled plasma optical or mass spectrometry used for elemental and isotopic analyses (ICPOES, ICPMS).

2 Methods

2.1 Instrumentation

Data are collected with six Mirion (formerly Canberra) Broad Energy intrinsic germanium detectors (BEGe) with carbon fiber endcaps and ultra-low background cryostats which are cooled with liquid nitrogen. The detectors are shielded with 10 cm of ultra-low background lead. Data acquisition is performed with Mirion DSA-1000 or Lynx digital signal processors running with Genie 2K software v.3. The specific BEGe detector design is important because it provides excellent efficiency at low gamma energies for ²¹⁰Pb acquisition without sacrificing efficiencies at high energies. Carbon fiber provides good transmission of the low energy ²¹⁰Pb emission which is otherwise attenuated by an aluminum endcap. Samples are typically run using a standardized four-day count time. Of two detector models, BEGe 3830 (38 cm² detector active area, 30 mm thickness) and larger BEGe 5030 (50 cm², 30 mm), the latter saves one day of counting and accomplishes in three days what the 3830 accomplishes in four.

2.2 Sample preparation and geometry

Foliage, litter, and soil samples are oven dried at 60°. Bulk soils are sieved or hand-picked to remove clasts and debris > 2 mm in diameter. Fine roots > 1 mm diameter or > 2 cm in length are removed by hand. Foliage and leaf litter (Oi and Oe horizon) are typically milled to <1 mm using a Wiley mill with stainless steel blades. Soil samples are loosely disaggregated as necessary by agate mortar and pestle and packed into 110 cm³ polyethylene petri dishes with snap closures. The petris are sealed with common electrical tape and rested for >2 weeks to allow for ²²²Rn ingrowth, although we will show that this approach does not quantitatively retain Rn (see also Murray et al., 1987, 2018). Our handling of the problem of Rn emanation from both laboratory samples and soils in situ is discussed below.

2.3 Calibration and Sample Self-Absorption

Gamma detector calibration is based on geometric efficiency, which is the proportion of photons emitted by the sample that are recorded by the detector, absent sample self-absorption of photons. Net efficiency includes self-absorption, which is dependent on each sample's specific elemental composition. We measure net efficiency directly by using a series of soils/sediment doped 1 % by weight with either uranium ore BL5 or thorium ore OKA2 which are available from Natural Resources Canada Certified Reference Material Project. Geometric efficiency for the standards is then calculated as the quotient of net efficiency and the standard self-absorption coefficient at each photopeak energy (described below). Geometric efficiencies are representative of the detector-sample geometric relationship and applicable to all sample unknown measurements. Efficiencies for photopeaks not represented in the standards are estimated by regression from adjacent photopeaks in the U or Th standards (e.g., ⁷Be, ²⁴¹Am, or ¹³⁷Cs; these are not known to have coincidence summing effects). Reported uncertainties on the standard activities is 0.2 % for U and 1.0 % for Th, and secular equilibrium is assumed for both.

Net efficiency for individual samples is calculated as the product of geometric efficiency determined from standards and the sample self-absorption at each energy of interest (Landis et al., 2012). To do this, self-absorption for each sample is measured using a planar uranium ore source (same diameter as sample) placed directly on top of the sample. This is performed as a second data acquisition following the sample “long count” which does not use the point source. Self-absorption at all energies is calculated using the method of (Cutshall et al., 1983), or in the case of non-uranium series radionuclides, is estimated by linear regression from the U-series photopeaks.

Calibration uncertainty estimated from geometric efficiencies of 6 standards of bulk density ranging from 0.5 to 200 g cm⁻³ is less than 2 % relative standard deviation for each of our detectors. Uncertainty of sample self-absorption derived from peak integration (below) contributes <1 %. Thus, our net efficiency calibration uncertainties are ∼2 % at the 1σ level.

2.4 Peak integration and activity calculation

A semi-automated peak integration routine is implemented in Excel worksheets (Fig. 2) (Landis et al., 2012). For each detector, peak shape parameters are measured across all energies either within the collected sample spectrum using peaks > 10 000 counts or using prior collection of a high-activity point source spectrum, by least-squares fitting of peaks using the Solver tool and unknowns μ, σ, L, H as below, where x is the channel energy, μ is the peak centroid, σ is Gaussian peak width, and L and H are low and high energy transitions of peak tails to logarithmic rather than Gaussian form.

$$\begin{array}{}\text{(1)}& p\left(x_i\right)=\left[\underset{-\mathrm{\infty }}{\overset{L}{\int }}{e}^{\frac{L\left(\mathrm{2}x-\mathrm{2}\mathit{\mu }+L\right)}{\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}}}}+\underset{L}{\overset{H}{\int }}{e}^{\frac{-{\left(x-\mathit{\mu }\right)}^{\mathrm{2}}}{\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}}}}\underset{H}{\overset{\mathrm{\infty }}{\int }}{e}^{\frac{H\left(\mathrm{2}\mathit{\mu }-\mathrm{2}x+H\right)}{\mathrm{2}{\mathit{\sigma }}^{\mathrm{2}}}}\right]/\underset{-\mathrm{\infty }}{\overset{\mathrm{\infty }}{\int }}p\end{array}$$

The peak shape model is then used to estimate the partial area of analyte peaks that are integrated digitally by summation of peak channel count rates. Partial peak integration reduces measurement uncertainty by avoiding peak tails which contribute disproportionately to integration error.

$$\begin{array}{}\text{(2)}& A={\displaystyle \frac{R}{f\cdot \mathit{\epsilon }\cdot p\cdot \mathit{\gamma }\cdot m}}\end{array}$$

Finally, radionuclide activity A [Bq kg⁻¹] is calculated following Eq. (2), where R is the integrated count rate (gross minus off-peak background count rate), f is the measured attenuation coefficient, ε^* is detector geometric efficiency, p is the partial peak integration area, γ is photopeak yield constant, and m is the sample mass [kg⁻¹] (Fig. 2).

Figure 2 Work flow for gamma spectrometry data reduction. Three Excel-based templates are used to process sample, attenuation, and calibration spectra. Required metrics for the fundamental calculation of Eq. (2), the parameters μ, σ, L, H, f, and ε^*, are determined as functions of photopeak energy (E).

2.5 Spectral Background Correction

In addition to off-peak background subtraction, all radionuclide peaks are also corrected for on-peak background contributions which are measured with composite background spectra totaling hundreds of days of count time. Backgrounds for each peak may variously include impurities in the detector housing and shielding, ambient Rn in the laboratory, artifacts of the gamma spectrum, and ambient construction materials in the laboratory facility.

2.6 Data Quality and Verification

Environmental gamma spectrometry is capable of producing percent-level precision on par with other capital analytical platforms such as ICP-MS. Precision in gamma spectrometry measures of radionuclide activity is easily documented because many radionuclides emit photons at multiple energies. These typically have variable coincidence summing effects that require correction at each energy, as well as sample self-absorption factors that also require correction at each energy. Concordance among measures of multiple photopeaks spanning the energy spectrum thus provides a robust estimate of precision.

For quality control measures we recommend reporting multi-line means and uncertainties for three radionuclides: ²²²Rn measured at ²¹⁴Pb (295, 352 keV) and ²¹⁴Bi (609 keV); ²²⁸Ra measured with up to four emission lines from ²²⁸Ac (209, 338, 463, 911 keV); and ²²⁸Th measured by ²¹²Pb (238 keV), ²⁰⁸Tl (538 keV), and possibly ²²⁴Ra (241 keV) (Fig. 3).

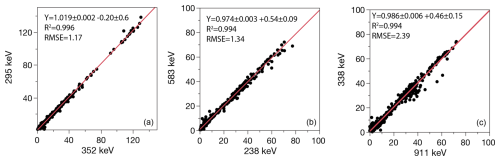
Figure 3 Correlations of multiple photopeaks for (a) ²²²Rn, (b) ²²⁸Th, (c) ²²⁸Ra. Lines show linear best fits.

The coefficient of variance (CV) or relative standard deviation (RSD) for multiple emission peaks for each of ²²²Rn, ²²⁸Th, and ²²⁸Ra provides an assessment of measurement accuracy and precision in the gamma spectrum (Fig. 4). These are in the 1 %–5 % range for typical crustal activity concentrations of 20 Bq kg⁻¹. ²²²Rn is important because it is often used as an indirect measure of ²²⁶Ra, with integration uncertainties 5–10 times lower (Fig. 4a), but also with this important caveat, that the actual values of the two measures may differ substantially due to geochemical disequilibrium caused by Rn leakage (Sect. 3.5).

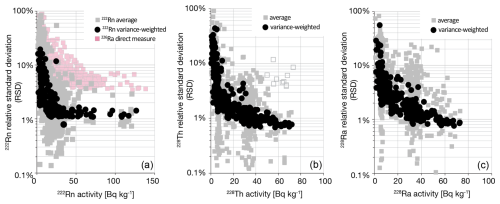
Figure 4 Average and variance-weighted average activities for radionuclides measured at multiple energies in the gamma spectrum, including (a) ²²²Rn, with comparison to direct measure of ²²⁶Ra; (b) ²²⁸Th; (c) ²²⁸Ra. ²²⁶Ra measurement is possible at a single emission line which is compromised by low photon yield and photopeak convolution with ²³⁵U, resulting in uncertainties 5–10 times higher than possible with, e.g., ²²²Rn daughter radionuclides.

2.7 Peak interference deconvolution

Multiple important radionuclides in the gamma spectrum suffer significant peak-peak overlap that requires deconvolution. Most notable are ⁷Be which has interference from both ²²⁸Ac (478 keV) and ²¹⁴Pb (280 keV) (Landis et al., 2012), and ²²⁶Ra which has interference from ²³⁵U at 185 keV and which approximately doubles its analytical uncertainty (Zhang et al., 2009). Our ⁷Be deconvolution regime is verified elsewhere using repeat measures of a single natural sample, since the known half-life of ⁷Be can be exploited to predict its change in concentration over monthly timescales (Landis et al., 2012). The ²²⁶Ra deconvolution regime can be tested against certified reference materials; however, the reported uncertainties for ²²⁶Ra in available standards typically exceeds 10 % and are therefore of limited use in verifying robust measurement of this radionuclide (more below in Sect. 8).

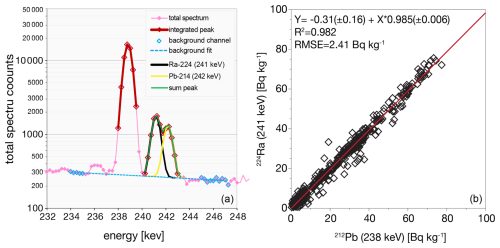
Deconvolution can also be tested using the measure of ²²⁴Ra (half-life 3.6 d, 241 keV) as a proxy for its parent radionuclide ²²⁸Th because of its photopeak overlap with ²¹⁴Pb at 242 keV. The peak deconvolution procedure is evaluated with the expectation that radioactive equilibrium is maintained, i.e., with a slope of 1 in correlation between the parent and daughter (Fig. 5). Here the slope = 0.985 ± 0.006 which shows a systematic error of just 1.5 ± 0.6 %.

Figure 5 (a) Measurement of ²²⁴Ra is possible in the gamma spectrum but requires deconvolution of its 241 keV emission from ²¹⁴Pb at 242 keV. (b) Accuracy of the ²²⁴Ra deconvolution procedure can be tested against ²¹²Pb (via ²²⁰Rn) measured at 238 keV.

3 Radionuclide measurements

3.1 ⁷Be and problem of detection

The defining limitation in LRC age model development is the problem of ⁷Be detection. The combination of low natural abundance, low photon yield (10.5 %), and short half-life (54 d) requires extraordinary efforts in both the logistics of sample collection and availability of instrument time to make these measurements possible. Samples should be measured within 1 month of collection and must be counted for 4 d or more per sample to define the ⁷Be soil depth profile (Fig. 6). Following these protocols ⁷Be may be detected to soil depths of 10 or more centimeters in humid or moist climates, which has important implications both for how soils are perceived to function and how age models are applied to soils (Landis et al., 2016).

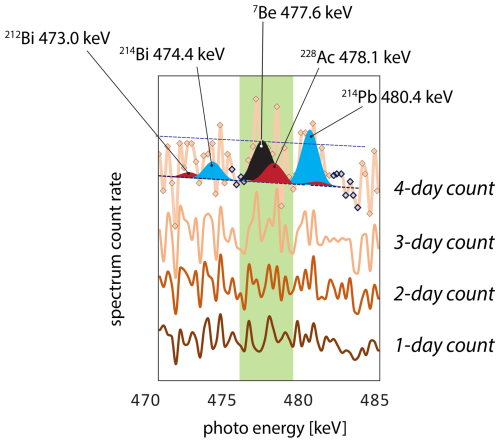
Figure 6 Elapsed measurement of the ⁷Be gamma photoregion over 1, 2, 3, and 4 d count times. The measured sample is soil from 5 cm depth, and ⁷Be activity is quantified as 1.8±1.0 Bq kg⁻¹ after 4 d. The modeled ⁷Be peak is shown in black, U-series peaks in blue, and Th-series peaks in red. MDL is shown with dashed line.

3.2 ²⁴¹Am and problem of detection

Demonstrating accuracy of LRC requires concordance with independent chronometers, and bomb-pulse ²⁴¹Am is the prime candidate due to its long half-life, limited solubility or bioavailability (in contrast to ¹³⁷Cs), and potential for its concurrent measurement in the gamma spectrum. The bomb-pulse has a well-known history of activity in the atmosphere (Appleby et al., 1991; Health and Safety Laboratory, 1977). Abundance of ²⁴¹Am is low, however, rarely exceeding 1 Bq kg⁻¹ in temperate soils, and is altogether undetectable in equatorial soils where fallout deposition was 10-times lower than mid-latitudes (Chaboche et al., 2021). Alternate measurement of Pu isotopes by ICPMS or AMS is becoming routine and may offer an alternative where ²⁴¹Am cannot be measured (e.g. Alewell et al., 2017).

3.3 ¹³⁷Cs and problem of geochemical mobility

In contrast to ²⁴¹Am, ¹³⁷Cs is easily measured in the gamma spectrum. However, it can be subject to biological cycling as a K analog especially where soil K may be deficient (Kaste et al., 2021). As a result, the shape of Am and Cs profiles can diverge remarkably (Fig. 7). ²⁴¹Am is always the preferred measure of bomb pulse. Still, where ²⁴¹Am and ¹³⁷Cs profiles appear consistent, ¹³⁷Cs may provide constraints on shape of the ²⁴¹Am profile when the latter is detection limited if it can be shown, e.g. by regression, that there is no systematic bias between the ²⁴¹Am and ¹³⁷Cs depth profiles or mass distributions.

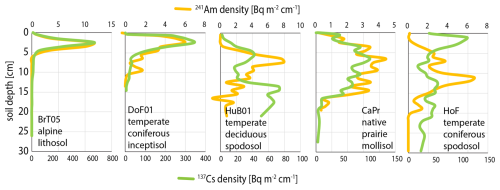
Figure 7 Depth profiles of ²⁴¹Am and ¹³⁷Cs in diverse soils. In all cases the cumulative ²⁴¹Am date is consistent with bomb-pulse peak of 1963–1964. Assigned calendar years are as follows: BrT05 = 1970.1, DoF01 = 1965.3, HuB01 = 1964.4, CaPr01 = 1964.2, HoF01 = 1958.1. In some cases, ¹³⁷Cs follows ²⁴¹Am closely, in others (especially spodosol) their divergence is pronounced and ¹³⁷Cs follows a “leaky cycle” whereby some portion may be strongly retained near the soil surface while any escaping this surface peak is rapidly flushed through the soil profile below.

3.4 Total ²¹⁰Pb

Total ²¹⁰Pb is the sum of both atmospheric (excess) and geogenic (supported) sources and is easily measured in gamma spectrum with BEGe detectors. The strongest source of error is self-absorption since this can vary by a factor of 2–3 through the soil profile. However, the low photon yield (4 %) can make measurement of supported ²¹⁰Pb challenging in soils with typical crustal uranium abundance. The four-day count time is thus important for providing adequate precision for defining ²¹⁰Pb_ex at the tail of its depth distribution (where ²¹⁰Pb_ex is calculated as ²¹⁰Pb_total minus ²²²Rn; see below).

3.5 ²²⁶Ra, the problem of radon emanation, and defining supported ²¹⁰Pb

The measure of ²²⁶Ra is important, in principle, for defining the activity of ²¹⁰Pb that is supported in soil by secular equilibrium with U-bearing minerals and organic matter (discussed in detail in Sect. 4). However, here we show that, due to endemic radioactive disequilibrium in soils, indirect measure of ²²²Rn should be preferred over direct measure of ²²⁶Ra for estimating supported ²¹⁰Pb. Secular equilibrium requires that radionuclides in a decay chain have equal activities, and we should observe this in the abbreviated chain ²²⁶Ra > ²²²Rn ≫ ²¹⁴Bi > ²¹⁴Pb ≫ ²¹⁰Pb provided that gaseous Rn can be retained within the sample (≫ indicates omitted radionuclide). Instead, we observe that ²¹⁴Pb and ²¹⁴Bi (indirect measures of ²²²Rn) underestimate ²²⁶Ra even in samples that are sealed and rested for the ingrowth period required for Rn to achieve equilibrium (5 half-lives or about 20 d) (Fig. 8). The obvious conclusion is that Rn emanates from packed soil samples during routine measure. Disequilibrium between ²²²Rn and ²²⁶Ra is difficult to assess in a single sample, because of high uncertainties on the ²²⁶Ra measure due in part to significant overlap from the primary ²³⁵U emission at 185.7 keV (Zhang et al., 2009).

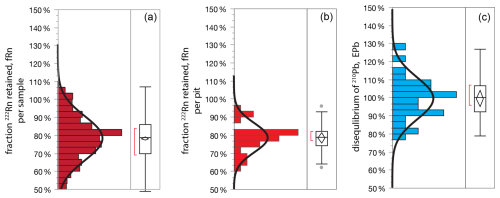
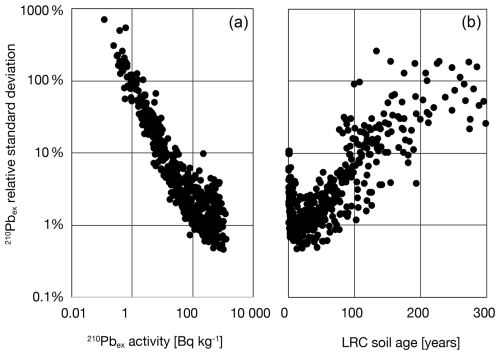
Figure 8 Rn retention by soils, (a) fraction ²²²Rn retained per sample in laboratory, calculated as ${}^{\mathrm{222}}\mathrm{Rn}{/}^{\mathrm{226}}\mathrm{Ra}$. The mean ²²²Rn disequilibrium factor fRn in this dataset on a per-sample basis is 77±15 % (SD, n=472, omitting samples with ²²⁶Ra < 20 Bq kg⁻¹). (b) Fraction ²²²Rn retained per soil pit, (c) laboratory disequilibrium between ²¹⁰Pb and ²²²Rn in deep soils, per soil pit, calculated as ePb = ${}^{\mathrm{210}}\mathrm{Pb}{/}^{\mathrm{222}}\mathrm{Rn}$.

In this dataset we quantify disequilibrium between ²²²Rn and ²²⁶Ra as fRn, or fraction Rn, which is simply the ratio of the two measures. (We acknowledge that the problem is somewhat more complicated because the effective volume of Rn in the detector shield will be greater than volume of the sample itself, due to its diffusion from the sample container into surrounding air). Among all soil pits the mean measured fRn = 79±1 % (± RSE, n=30) (Fig. 8). Importantly, the variance of fRn within a single pit is much smaller than among pits [p<0.0001], which means that fRn is a property of the geochemistry of individual soils (with respect to hosting of Ra in primary vs. secondary minerals, grain size, susceptibility to chemical weathering, geologic age, etc.).

3.6 Experimental confirmation of ²²⁶Ra accuracy and ²²²Rn emanation

Affirming the accuracy of ²²⁶Ra measurements is foundational for understanding Rn emanation, and therefore for interpreting ²¹⁰Pb in the soil profile. Here we confirm the accuracy of direct ²²⁶Ra measurements (186 keV) against certified reference materials (CRMs) (Fig. 9). Performance is excellent with standard 4 d count times (Fig. 9a). We note that analytical uncertainties thus achieved are typically far better than those of the certification process itself. This reflects the difficulties in robust measure of ²²⁶Ra which requires long count times and corrections for self-absorption and deconvolution (Tasker et al., 2019).

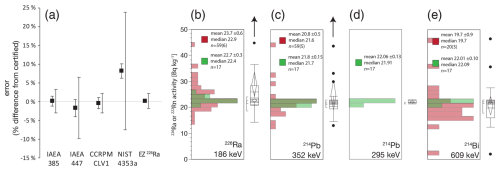
Figure 9 (a) FRNA values for ²²⁶Ra determination in certified reference materials IAEA-385 (Irish sea sediment), IAEA-447 (moss-soil), CCRMP CLV-1 (spruce needle), NIST-4353a (Rocky Flats soil). Eckert and Ziegler single isotope solution (EZ ²²⁶Ra) is used as an in-house calibration material. Error bars are 1σ standard deviations for analysis at FRNA, larger error bars show certification uncertainties. (b–e) Distributions of results for IAEA-385 certification measurements (red) and FRNA analysis (green) for individual emission lines of ²²⁶Ra and the ²²²Rn daughters ²¹⁴Pb and ²¹⁴Bi.

The IAEA-385 material is the most rigorously-calibrated soil standard available to date and is critical to our ability to validate high-quality gamma spectrometry (International Atomic Energy Agency, 2013; Pham et al., 2008). Even so, the original recommended ²²⁶Ra activity of 22.7 ± 0.7 Bq kg⁻¹ (Pham et al., 2005) is 3.6 % higher than the eventual certification value of 21.9 Bq kg⁻¹. The lower value derives from the averaging of direct ²²⁶Ra measurements with lower estimates from ²¹⁴Pb (352 keV) and ²¹⁴Bi (609 keV) (Fig. 9b–e). The latter should be viewed as suspect since both Rn emanation and coincidence summing losses can bias the ²²²Rn daughters too low. FRNA measurements appear to confirm a systematic ²²²Rn loss of 3.4 % as the difference between ²²⁶Ra activities (22.7 ± 0.3) and ²²²Rn (21.98 ± 0.07) [p=0.0186].

For analysis of sample unknowns we sought to confirm the accuracy of our ²²⁶Ra measures and therefore that Rn disequilibrium is due to Rn loss and not an analytical artifact (Syam et al., 2020). We performed an experiment with NIST-traceable ²²⁶Ra standard solution (Eckert and Ziegler; certified uncertainty <2 %). which is important to verify that ²²⁶Ra is measured accurately and with high enough activity to measure it with percent-level precision (here approximately 360 Bq kg⁻¹). A second calibrated ²²⁸Ra solution was prepared by dissolution of thorium ore OKA-2. Accuracy of both Ra source calibrations was previously confirmed by isotope-dilution thermal ionization mass spectrometry (Landis et al., 2018). Briefly, both the ²²⁶Ra and ²²⁸Ra standard solutions were co-precipitated in a wet synthesis of MnO₂ from KMnO₄ and MnCl₂ at pH ∼ 9. To replicate a typical soil sample in 110 cm³ petri geometry, the synthesized Ra-MnO₂ was air dried onto a bed of quartz sand. The Ra-Mn-sand thus produced represents a worst-case scenario for Rn emanation because all Ra is contained in amorphous or microcrystalline secondary mineral.

Samples were packed into our standard polypropylene petri as for a soil sample. The petri was first closed with electrical tape and measured serially to observe Rn ingrowth. Yields of both ²²⁶Ra and ²²⁸Ra are within error of 100 % of certified or expected values (Fig. 10). Short-lived ²²⁰Rn (aka thoron, half-life = 56 s) is fully retained by the sample, but grows in following the half-life of intermediary ²²⁴Ra (3.6 d) which is expelled from the initial suspension of MnO₂ by alpha recoil.

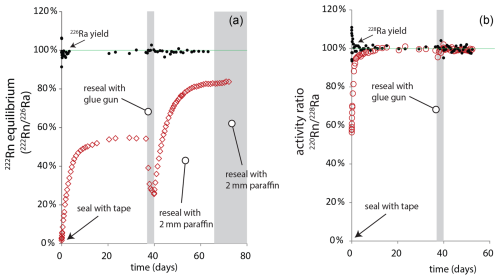
Figure 10 Experimental confirmation of ²²²Rn emanation from 110 cm³ soil laboratory samples, (a) ²²²Rn and ²²⁶Ra source, (b) ²²⁰Rn and ²²⁸Ra source. Closed symbols show yield of ²²⁶Ra or ²²⁸Ra from the experiment, open symbols show corresponding Rn yield or equilibrium as the $\mathrm{Rn}/\mathrm{Ra}$ activity ratio.

In contrast, for long-lived ²²²Rn we observed an equilibrium fRn of just 55 % after approximately thirty days. The sample was then resealed using hot glue, but this reduced Rn retention, presumably due to porosity in the glue that visibly forms upon cooling. Finally, the sample was encased in 2 mm of paraffin wax. This final step increased fRn to 85 %, but the impracticality of the method coupled with imperfect Rn retention is a fatal strike against its routine use in our laboratory.

Our subsequent efforts to seal samples under vacuum in aluminized Mylar bags improve Rn retention up to 90 %–95 % for our 110 cm³ petri (Mauring and Gäfvert, 2013), but we have not standardized this approach due to remaining uncertainty in precise quantification of retention, the creation of additional laboratory waste and, in the face of these problems, the uncertain value of improving the indirect measure of ²²⁶Ra to defining ²¹⁰Pb_ex (see below).

4 Defining excess Pb-210 (²¹⁰Pb_ex)

FRN age models are based on the atmospheric component of ²¹⁰Pb, which in soils and sediment must be separated mathematically from ²¹⁰Pb that is supported by in situ production from U-series decay in soil minerals. By convention atmospheric ²¹⁰Pb is measured as the excess over that which is supported (²¹⁰Pb_S) by its long-lived radioactive precursor ²²⁶Ra, i.e., ²¹⁰Pb_ex = ²¹⁰Pb minus ²²⁶Ra, with the assumption that ²²⁶Ra = ²¹⁰Pb_S. Due to analytical constraints described above, ²²⁶Ra is routinely measured indirectly using ²²²Rn with the assumption that equilibrium is maintained between the two. We have already shown this is not accomplished in typical sample preparation.

Further, there is the problem of Rn emanation from soils in situ: the very process that produces excess ²¹⁰Pb in the atmosphere yields a ²¹⁰Pb deficit in soil. This means that supported ²¹⁰Pb in soils is likely to be overestimated if measured by ²²⁶Ra. This leaves two open questions, (1) what is the correct metric for supported ²¹⁰Pb in situ, and (2) how do we measure this in routine data collection in the laboratory? To clarify these problems, we introduce the term Pb enrichment, ePb, which is the ratio of ²¹⁰Pb to ²²²Rn in deep soil samples believed free of atmospheric ²¹⁰Pb. Importantly, for all soil pits we have measured ePb = 102±3 % (± RSE, n=30) which means that supported ²¹⁰Pb is typically in equilibrium with measured ²²²Rn. This is best illustrated in the soil depth profile where total ²¹⁰Pb converges asymptotically with ²²²Rn, whereas both are overestimated by ²²⁶Ra (Fig. 11). Interestingly, this implies that Rn loss from the measured sample is comparable to loss in the soil in situ, and further that, as observed above, Rn emanation from standard laboratory samples relates to a physical property of the soil itself.

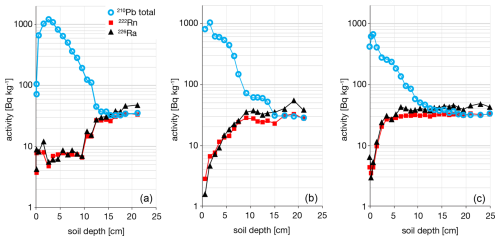
Figure 11 Defining excess ²¹⁰Pb in soils. (a) Hubbard Brook Experimental Forest (HuB01), (b) Experimental Lakes Area soil 302-1, (c) Harvard Forest LTER (HaF01). Total ²¹⁰Pb typically converges with ²²²Rn at depth which indicates that ²²²Rn is an appropriate estimate of supported ²¹⁰Pb.

We therefore conclude the following regarding the definition of ²¹⁰Pb_ex in soils,

1. ²²⁶Ra is not an appropriate direct measure of supported ²¹⁰Pb due to chronic emanation of ²²²Rn from the soils in situ.

2. in situ ²²²Rn emanation in the soil profile can be assessed directly by gamma measurements, as an asymptotic difference between ²²⁶Ra and ²¹⁰Pb in deep soils.

3. measure of ²²²Rn by daughters ²¹⁴Pb and ²¹⁴Bi provides excellent precision and reproducibility among multiple emission lines, 5–10 times better than possible with direct measure of ²²⁶Ra.

4. Rn emanation from the laboratory sample is both pronounced and systematic, despite sealing of containers and incubating >18 d following standard practice.

5. nonetheless, ²²²Rn measured in the sample typically converges with ²¹⁰Pb, or is asymptotic with ²¹⁰Pb, suggesting that ²²²Rn measure in the laboratory sample is the best available option for defining ²¹⁰Pb_ex in soil.

For defining ²¹⁰Pb_ex at each soil depth we use the following expression. The calculation therefore uses a direct measure of ²²²Rn at each depth to accommodate changes in soil organic matter, mineral abundance, and bulk density, but assumes a correction for Rn emanation rate for the full the soil profile (Landis et al., 2016):

$$\begin{array}{}\text{(3)}& {}^{\mathrm{210}}{\mathrm{Pb}}_{\mathrm{ex}}={}^{\mathrm{210}}{\mathrm{Pb}}_T-{}^{\mathrm{222}}\mathrm{Rn}\left(e\mathrm{Pb}\right)\end{array}$$

Calculation of ²¹⁰Pb_ex is not provided in the dataset but can be performed following Eq. (3). Propagated uncertainties in ²¹⁰Pb_ex when calculated by Eq. (3) are shown in Fig. 12.

Figure 12 Propagated uncertainties for ²¹⁰Pb_ex as function of (a) total ²¹⁰Pb_ex activity, (b) LRC soil age.

5 Demonstrating LRC concordance with bomb pulse ²⁴¹Am

Demonstrating concordance of LRC ages with independent chronometers is important for verifying both the suitability of soils for chronometry and veracity of data production (Landis et al., 2024b). We report ²⁴¹Am activities for this purpose, but it should be noted that peak bomb-pulse deposition is indicated at the layer of maximum ²⁴¹Am density (Bq m⁻² cm⁻¹) rather than activity concentration since the latter is skewed by changes in bulk density, especially at the soil surface. ²⁴¹Am density is readily calculated from the data provided. In some cases, the shape of ²⁴¹Am bomb-pulse peak can be grossly distorted due to acceleration and deceleration of colloid migration in the soil profile (Landis et al., 2024a), and in these cases the cumulative ²⁴¹Am curve becomes an alternate tool for identifying peak bomb fallout since the history of ²⁴¹Am in the atmosphere is well known (Appleby et al., 1991; Health and Safety Laboratory, 1977).

6 Assessing uncertainties on radionuclide measurements

Our reported uncertainties for radionuclide activities are internal estimates which are propagated from uncertainties on peak integration; this includes background subtraction, partial-peak integration fraction, and deconvolution where needed. These provide a direct assessment of measurement quality related to total radionuclide activity, spectral complexity, and related Poisson statistics. Uncertainties due to efficiency calibration and self-absorption correction are not included in reported uncertainties because they are fixed and therefore easily consolidated in a second step by propagating an additional 2 % uncertainty as described in Sect. 2.3. We have not established the extent to which calibration uncertainties may autocorrelated across different radionuclide energies. These external uncertainties are therefore assessed here for user consideration, for example, when comparing measurements in this dataset to those from other laboratories.

Z-scores to assess radionuclide uncertainty estimates

The accuracy of reported integration uncertainties can be assessed using multiple emission lines for a single radionuclide, since each must conform to the same true mean activity value. We show this by means of Z-score, which is the difference between emission line activities, normalized by the propagated uncertainty for the difference. The standard deviation of Z should be equal to 1 if the estimated integration uncertainties accurately represent the true distribution of random error in the measurements (Fig. 13). We observe standard deviations in Z of 0.8, 1.2, and 1.4 for ²²²Rn, ²²⁸Th, and ²²⁸Ra, respectively. These are close to 1 which implies that the integration uncertainties are robust. In the case of ²²⁸Th and ²²⁸Ra the real uncertainties are somewhat underestimated which means that uncertainties in calibration contribute an additional error, and one that is similar in scale to uncertainties in integration, i.e., if similar errors are propagated the result is a 40 % higher than either, $\surd ({\mathrm{1}}^{\mathrm{2}}+{\mathrm{1}}^{\mathrm{2}})=\mathrm{1.4}$.

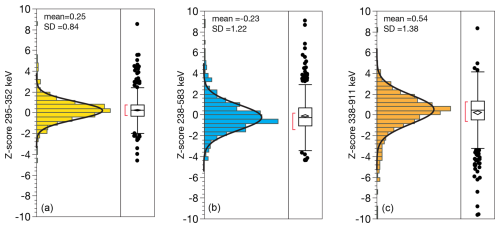
Figure 13 Distribution of Z-scores for multiple emission lines of (a) ²²²Rn (295, 352 keV); (b) ²²⁸Th (238, 583 keV); (c) ²²⁸Ra (338, 911 keV). Z expresses the difference between two measures in units of σ, calculated as the difference between two measures of activity, divided by propagated uncertainty of the two measures.

On the other hand, our prior assessment suggests that integration uncertainties are overestimated by on the order of 30 %, based on the unique experiment of measuring radioactive decay of ⁷Be since the true value of the sample is known based on its rate of decay, and estimated uncertainties can be evaluated against the observed dispersion of measurements around this known value (Landis et al., 2012). Overestimation of integration errors is consistent with our observed Z<1 for the ²²²Rn lines comparison above. That uncertainties for ²²⁸Th and ²²⁸Ra are greater than for ²²²Rn suggests that the interaction of coincidence-summing and self-absorption effects yields higher error in calibration, since these are not handled independently in our calibration routine, i.e., by using a Th point source instead of U for Th-series photopeaks. Future work is required to determine whether one ²²⁸Ra measurement may be preferred over others (e.g., among the ²²⁸Ac photopeaks at 209, 338, and 911 keV).

7 Spectrum accuracy evaluated using ²²⁸Th : ²²⁸Ra

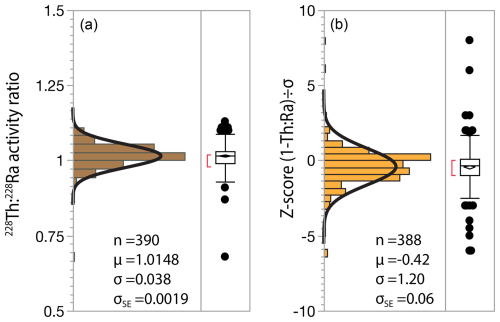
The ²²⁸Th : ²²⁸Ra ratio is an important metric for evaluating accuracy of gamma measurements since it can generally be assumed to have an equilibrium value of 1 due to short half-lives of 1.9 and 5.8 years, respectively. To ensure this is true we omit samples with LRC ages <20 years or ²²⁸Ra <10 Bq kg⁻¹ since these may have true ²²⁸Th : ²²⁸Ra disequilibrium due to variable uptake of Th and Ra during plant growth (Landis, 2023). The mean ²²⁸Th : ²²⁸Ra ratio for the data set is 1.015±0.038 SD, ±0.002 SE (n=390), showing a minor bias of 1.5 % which is within typical calibration uncertainty. Importantly, the standard deviation for Z (for the difference between ²²⁸Th : ²²⁸Ra and 1) = 1.20, which shows that the estimates of uncertainties are reasonable (Fig. 14).

Figure 14 Assessing analytical accuracy using the measured ²²⁸Th : ²²⁸Ra ratio in soils. (a) Measured ²²⁸Th : ²²⁸Ra ratio for all soils, (b) Z-score for difference between measured ratio and 1.

8 Certified Reference Materials

Availability of a few high-quality certified reference materials provides a means for external validation of environmental gamma data. We recommend IAEA-385 (sediment), IAEA-447 (moss soil), and NRC CLV-1 (spruce twig), since these have rigorous quality control and uncertainties low enough (typically <5 %) to allow verification of high-precision methods. Performance of our methods against these standards for radionuclides in addition to ²²⁶Ra is reported elsewhere with errors against certified values <5 % (Landis et al., 2012, 2016).

9 Detection limits

Detection limit applies to total radioactivity in the detector shield [Bq], which is the product of mass and concentration. This means that detection is inversely dependent on sample bulk density since the sample volume is fixed. Detection is also inversely dependent on sample count time following Poisson counting statistics. Finally, detection is also influenced by composition of the sample with respect to other elements and radionuclides because these influence photopeak backgrounds through Compton scattering. Because detection limits thus vary based on sample mass, composition, and count time they are not easily compiled and compared. We instead defer to reported uncertainties so that the value or weight of each datum can be independently assessed by users on this basis. Given this caveat, estimated detection limits for four-day count times, 100 g samples, and approximately crustal-average U and Th content are approximately as follows: ⁷Be (0.5 Bq kg⁻¹); ²¹⁰Pb (1.5 Bq kg⁻¹); ¹³⁷Cs (0.3 Bq kg⁻¹); ²⁴¹Am (0.15 Bq kg⁻¹); ¹⁸⁶Ra (2.5 Bq kg⁻¹); ²²²Rn (0.2 Bq kg⁻¹); ²²⁸Th (0.2 Bq kg⁻¹); ²²⁸Ra (1.0 Bq kg⁻¹).

10 Data versions, omissions, and error codes in the database

Multiple data reduction generations are represented in the database, with notable differences being the introduction of new photopeaks such as 209, 338, and 583 keV in later versions. Data fields are empty in preceding analyses.

In some rare cases (e.g., deep peat cores), samples that are unable to fill a 110 cm³ petri are run instead in 10 cm³ petris. The lower volume incurs a corresponding loss in data quality due to low total activity and resulting counting statistics. Data quality for the smaller 10 cm³ petri is poor and our use of them is rare. These data are not reported in this database at the present time, but may be provided upon request.

The error #NUM! in some uncertainty estimates is a peak integration error typically resulting for integration of small peaks that are near detection. This can propagate through deconvolution regimes, i.e. error in uncertainty of ²²⁸Ac integration will produce error in uncertainty for ⁷Be. For purposes of error propagation, the error can reasonably be estimated by assuming 100 % relative uncertainty, i.e., equal to the value. Future work aims to eliminate this error.

11 Reported data fields

The reported data are tabular in form and may be downloaded (below) as an Excel spreadsheet. Row one is data identifier 1. Row two is data identifier 2, and row three is column units or identifier 3. Subsequent rows list data per sample. Reported metadata and data include the following across columns:

1. column A: pit code: unique identifier for the soil pit.

2. column B: sample name: unique identifier for the soil pit depth interval.

3. column C: sample description: including horizon and/or depth interval.

4. column D: horizon code: soil taxonomic horizon description.

5. column E: interval mass [kg m⁻²]: total mass of fine soil fraction (<2 mm) for the collected depth interval.

6. column F: soil depth [cm]: starts at soil surface = 0 rather than at mineral soil surface.

7. column G: R_acc; accumulative ⁷Be : ²¹⁰Pb ratio for overlying soil layers used in implementation of LRC model.

8. column H: propagated uncertainty (1σ) for R_acc.

9. column I: relative standard deviation (RSD) of R_acc.

10. column J: count time [s] for collected gamma spectrum.

11. columns K-AP: paired columns with activity concentrations [Bq kg⁻¹] and internal uncertainties for the following radionuclide: ²¹⁰Pb (46 keV), ⁷Be (477 keV), ²⁴¹Am (60 keV), ¹³⁷Cs (662 keV), ²³⁴Th (63 keV), ²²⁶Ra (186 keV), ²²²Rn (295, 352, 609 keV), ²²⁸Th (238, 538 keV), ²²⁸Ra (338, 911 keV), ⁴⁰K (1460 keV).

12 Data availability

The data described in this manuscript are freely available to the public (https://doi.org/10.17632/cfxkpn6hj9.1; Landis, 2025).

13 Conclusions

The central limitation to advancing chronometry of modern terrestrial biogeochemistry, including atmosphere-soil interaction and soil processes, is availability of required radionuclide data. We hope that by providing a large, open-access dataset we can help catalyze interest among new research groups and funding agencies in making new investments towards similar data acquisition efforts.