A hydrogeomorphic dataset for characterizing catchment hydrological behavior across the Tibetan Plateau

Hydrologic and geomorphic processes are intricately linked within the Earth system, jointly characterizing terrestrial hydrological behaviors and biogeochemical cycles across diverse temporal and spatial scales. The Tibetan Plateau provides an ideal setting for investigating the interactions between hydrological and geomorphic processes in a largely pristine natural environment. Nonetheless, the interactions remain largely unknown due to challenging physical conditions and data limitations. This study presents the inaugural version of a hydrogeomorphic dataset encompassing 18 440 catchments across the region. The dataset comprises 18 hydrogeomorphic metrics along with, in particular, the width-function-based instantaneous unit hydrograph (WFIUH) of each catchment. We find that the peak flow of WFIUH is positively related to slope and curvature but negatively related to catchment area, perimeter, length and circularity. The relationships of time to peak with the hydrogeomorphic metrics are similar to those of peak flow but in an oppositive direction. Catchment concentration time shows a positive relationship with catchment size but a strong negative correlation with catchment slope. The validity of the derived WFIUH has been confirmed by its successful integration into an hourly hydrological model for simulating flash-flood events. Uncertainties in the WFIUH can be attributed to the resolution of the digital elevation model (DEM) and the methods employed for calculating flow velocity. The dataset is publicly available via the Zenodo portal: https://doi.org/10.5281/zenodo.8280786 (Guo and Zheng, 2023). It can contribute to advancing our understanding of catchment hydrological behaviors and can provide simple and fast-routing unit hydrograph calculation for ungauged catchments in the Tibetan Plateau and hence improve water resources management and disaster mitigation in the region and its downstream areas.

1 Introduction

Hydrologic and geomorphic processes are intricately linked within the Earth system, jointly characterizing terrestrial hydrological processes and biogeochemical cycles across diverse temporal and spatial scales. The interactions between these processes play a critical role in governing water flow, shaping landforms, and influencing sediment and nutrient transportation within ecosystems (Babar, 2005; Scheidegger, 1973; Sidle and Onda, 2004). The exploration of the interactions can be traced back to Horton's foundational contributions (Horton, 1945) and the classical works of Strahler (1957), Kirkby (1976), and Rodríguez-Iturbe and Valdés (1979). Since then, extensive endeavors have been undertaken in hydrology and geomorphology to investigate the hydrologic behavior of a catchment in response to its geomorphic attributes (Jenson, 1991).

Hydrogeomorphic data consisting of various geomorphic attributes (e.g., slope, elevation, curvature and catchment shape attributes) have demonstrated value in predicting hydrological behavior for ungauged basins (Esper Angillieri, 2008), mapping flood-prone zones (Lindersson et al., 2021) and determining the groundwater potential zones. On top of the morphologic or topographic metrics describing catchment properties, the geomorphologic instantaneous unit hydrograph (GIUH) introduced by Rodríguez-Iturbe and Vald́es (1979) is of utmost interest for hydrologists to derive hydrographs in the absence of hydrologic data (Bhaskar et al., 1997; Jain et al., 2000; Nasri et al., 2004; Nowicka and Soczynska, 1989; Kumar et al., 2007). The concept of GIUH was extended by Gupta et al. (1980) to theoretically deduce the unit hydrograph based on geomorphology, topographic parameters and hydrographic parameters. GIUH assumes that the probability distribution of the water droplet travel time is exponential, which, however, lacks practical physical meaning (Gupta and Waymire, 1983; Kirshen and Bras, 1983; Rinaldo et al., 1991). The assumption is arguable, and it is also challenging to determine flow velocity while deriving GIUH (Rodríguez-Iturbe and Valdes, 1979; Troutman and Karlinger, 1985). An alternative geomorphology-based unit hydrograph is based on the geomorphic width function (Kirkby, 1976). The width function is commonly considered to be one of the most important geomorphologic and hydrologic features in quantifying the influence of the river network on catchment hydrologic processes (Mesa and Mifflin, 1986; Naden, 1992), which determines the shape of the instantaneous unit hydrograph (Botter and Rinaldo, 2003). Franchini and O'Connell (1996) compared the width-function-based instantaneous unit hydrograph (WFIUH) against GIUH and suggested that WFIUH is more physically consistent and more practical.

The Tibetan Plateau is known as the water tower of Asia, supplying water to almost 2 billion people (Yao et al., 2012; Li et al., 2022; Mtamba et al., 2015). Hydrogeomorphic characteristics of catchments within the Tibetan Plateau are unique, with little human intervention (Yao et al., 2022; Mölg et al., 2014). The geographical uniqueness of the Tibetan Plateau provides ideal opportunities to explore the interactions between hydrologic and geomorphic processes. However, hydrogeomorphic data of catchments across the Tibetan Plateau are still too limited for a systematic investigation of the hydrogeomorphic process in the region. Particularly, the Tibetan Plateau is experiencing more extreme precipitation events and floods (Ge et al., 2019; Yang et al., 2022), which makes it imperative to develop a comprehensive hydrogeomorphic dataset to inform flood modeling and adaptive watershed management.

This research aims to provide an inaugural version of the hydrogeomorphic dataset for catchments over the Tibetan Plateau. The dataset includes 18 hydrogeomorphic measurements of 18 440 catchments within the plateau, which are derived from a high-resolution digital elevation model (DEM) or compiled from existing products. Most importantly and uniquely, the research provides the first dataset of WFIUH for each catchment, which can be used to investigate the spatial heterogeneity of hydrological behavior across the Tibetan Plateau. The derived WFIUHs are tested and validated as applied to flood modeling for gauged catchments. This dataset is expected to contribute to a better understanding of hydrogeomorphic processes and to facilitate hydrological modeling of catchments across the Tibetan Plateau.

2 Study area and data

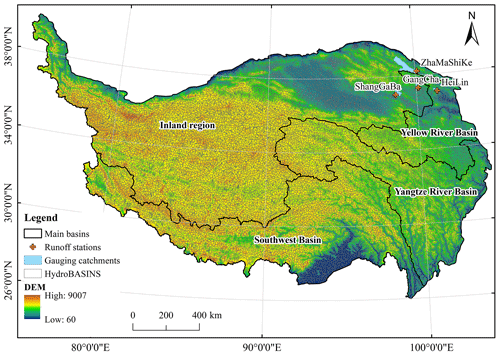
The Tibetan Plateau (TP) is situated between 26 to 40° N and 73 to 105° E and has a mean elevation of more than 4500 m, occupying about 2.5 × 10⁶ km². The TP is the highest and most extensive highland in the world. In addition to having the largest cryospheric extent outside the polar region, the TP also serves as the source region for all major rivers in Asia. Consequently, it has been widely acknowledged as the driving force behind both regional and global environmental change (Kang et al., 2010). The Mekong River, the Yellow River, the Yangtze River, the Yarlung Tsampo (Brahmaputra), the Indus and the Karnali all originate on the Tibetan Plateau and support hundreds of millions of people downstream. Due to the harsh and complex natural environment, the Tibetan Plateau is a typical ungauged area in China. Within the boundary of China, the Tibetan Plateau can be roughly divided into several basins, namely the inland-region basin, the Yellow River basin, the Yangtze River basin and the southwest basin (Fig. 1).

Figure 1 Elevation and boundaries of 18 440 HydroBASINS catchments across the Tibetan Plateau.

In this study, the hydrogeomorphic dataset we developed covers 18 440 catchments across the Tibetan Plateau. The boundaries of the catchments are determined according to the HydroBASINS dataset, where the 12th-level catchments are considered (https://www.hydrosheds.org/products/hydrobasins, last access: 19 March 2024). To successfully derive the width function for each catchment, the flow direction raster map must first be produced. The Tibetan Plateau has numerous endorheic basins (mainly in the inland region in Fig. 1), and the algorithms applied to determine flow directions of endorheic and exorheic basins can be slightly different (e.g., Prusevich et al., 2022). As this study does not focus on the algorithms determining flow direction but mainly on generating the WFIUH for flash-flood modeling, we use the flow direction raster map from HydroSHEDS (https://www.hydrosheds.org/hydrosheds-core-downloads, last access: 19 March 2024), which is based on the DEM from NASA's Shuttle Radar Topography Mission (SRTM) with a spatial resolution of around 90 m (Lehner et al., 2008).

The land cover data product FROM-GLC (Finer Resolution Observation and Monitoring-Global Land Cover released by Gong et al. (2019) is used in this study to estimate the Manning coefficient in calculating flow velocity. The spatial resolution of the land cover data is 10 m. It is resampled by the bilinear approach to be consistent with the flow direction map. For hydrological modeling validity, hourly rainfall and streamflow data of four hydrological stations are obtained from China's Annual Hydrological Report. Boundaries of the 18 440 catchments and locations of the hydrological stations are shown in Fig. 1.

3 Methods

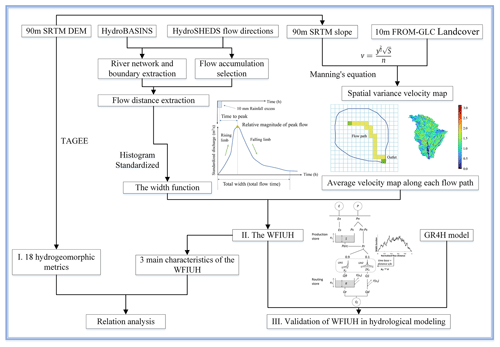
The overall framework for producing the hydrogeomorphic dataset for catchments over the Tibetan Plateau is shown in Fig. 2. The framework mainly consists of three procedures, i.e., extracting critical hydrogeomorphic metrics from the DEM or existing data products, deriving width function for catchments based on terrain analysis, and generating WFIUH for all catchments. The derived WFIUH is then tested by incorporating it into a hydrological model to simulate hydrological processes at a catchment scale.

Figure 2 Framework for developing catchment-scale hydrogeomorphic dataset of the Tibetan Plateau.

3.1 Catchment-scale hydrogeomorphic metrics

In this dataset, 18 hydrogeomorphic metrics at a catchment scale are retrieved from the DEM or compiled from existing datasets. The hydrogeomorphic metrics are closely related to hydrologic and geomorphic processes for the catchments, including area, the longitude of the centroid, the latitude of the centroid, mean elevation, slope, aspect, northness, eastness, perimeter, catchment length, catchment width, elongation, circularity index, form factor, shape index, Gaussian curvature, hillshade, horizontal curvature and vertical curvature. Definitions of each metric are shown in Table 1.

Several topographic and geomorphic attributes are gained from a package called Terrain Analysis in Google Earth Engine (TAGEE) (Safanelli et al., 2020) using Google Earth Engine platforms. The curvature shows the complexity of the undulation of the ground, and it is a quantitative measure of curvature degree and change point on the terrain surface. The horizontal curvature indicates the degree of curvature and the change of the surface along the horizontal direction, which could affect the convergence and dispersion of water flow. The vertical curvature is the degree of elevation change along the maximum slope of the ground slope, which could affect the speed of water flow, resulting in different erosion or accumulation rates. Mean curvature and the Gaussian curvature both characterize the comprehensive curvature features. According to Safanelli et al. (2020), northness and eastness can be derived from the aspect. The aspect and derived products, such as northness and eastness attributes, can be linked to the potential solar irradiation on the terrain. Mathematical expressions of these metrics, listed in Table 1, can be found in Florinsky (2016). It is worth noting that the shape index (SI) is a continuous numerical form of Gaussian landform classification proposed by Koenderink and Van Doorn (1992). The range of the shape index is −1 to 1. When the value is negative, the surface is concave, and when the value is positive, the surface is convex. When the absolute value of the shape index is within 0.5–1.0, the surface is elliptical. When the absolute value of the shape index is within 0–0.5, the surface is hyperbolic. The shape index expression is as follows:

$$\begin{array}{}\text{(1)}& \mathrm{SI}={\displaystyle \frac{\mathrm{2}}{\mathit{\pi }}}\arctan {\displaystyle \frac{H}{\sqrt{H^{\mathrm{2}}-K}}}.\end{array}$$

In the formula, H and K are parameters used to characterize the shape of the surface (such as ridge or valley, convex or concave). For illumination of the datasets, the expressions of circularity index (CI), form factor (R_f) and elongation ratio (R_e) are presented, respectively, as follows:

$$\begin{array}{}\text{(2)}& {\displaystyle }\mathrm{CI}={\displaystyle \frac{A_{\mathrm{catchment}}}{A_{\mathrm{circle}}}},\text{(3)}& {\displaystyle }{R}_{\mathrm{f}}={\displaystyle \frac{A_{\mathrm{catchment}}}{L_{\mathrm{catchment}}^{\mathrm{2}}}},\text{(4)}& {\displaystyle }{R}_{\mathrm{e}}={\displaystyle \frac{L_{\mathrm{circle}}}{L_{\mathrm{catchment}}}},\end{array}$$

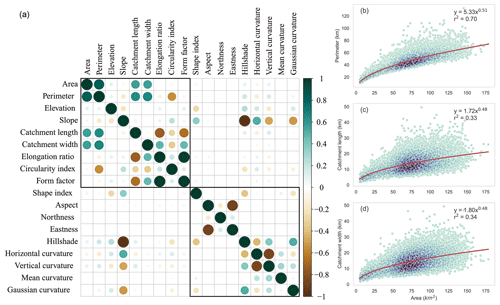
where A_catchment and L_catchment are the area and length of a catchment. A_circle is the area of a circle whose perimeter equals the watershed's perimeter. L_circle is the diameter of a circle that equals the catchment area. The circularity index represents the ratio of the catchment area to the area of a circle with an equivalent perimeter. It ranges between 0 and 1. The catchment is closer to a circular shape when presenting a higher CI value. The form factor is the ratio of catchment area to the squared catchment length. A higher R_f indicates a more fan-shaped catchment. The elongation ratio is the ratio of L_circle to catchment length. A smaller value of R_e reflects a more elongated catchment.

Metrics such as area, perimeter, catchment length, catchment width, elongation ratio, circularity index and form factor are retrieved from HydroBASINS sub-catchment shapes. The elevation and slope metrics are derived from the SRTM DEM, with a spatial resolution of around 90 m. Before retrieving the metrics for the Tibetan Plateau domain, all the maps are reprojected to the same coordination system.

Table 1 Descriptions of 18 hydrogeomorphic metrics provided in TPHGD dataset.

3.2 Width function from DEM

The width function (WF) of a catchment is more informative than a single hydrogeomorphic metric in reflecting runoff response to catchment landforms. The width function is defined as the probability measure at a given distance x to the outlet of the ith link measured along with the river network (Rinaldo et al., 1995). With the assumption that every water drop in the channel network travels to the outlet at the same velocity, mathematically, the width function W(x) is expressed as follows:

$$\begin{array}{}\text{(5)}& W\left(x\right)={\sum }_{i=\mathrm{1}}^{n}b(x;x_i^{\mathrm{u}},x_i^{\mathrm{d}}),\end{array}$$

where n is the number of links in the network, $x_i^{\mathrm{u}}$ and $x_i^{\mathrm{d}}$ are the distances of the upstream and downstream ends of link i from the outlet, and the function b(x) is expressed as

$$\begin{array}{}\text{(6)}& b\left(x;x_i^{\mathrm{u}}{x}_i^{\mathrm{d}}\right)=\left\{\begin{array}{cc}\mathrm{1},& x_i^{\mathrm{d}}\le x<x_i^{\mathrm{u}}\\ \mathrm{0},& \mathrm{otherwise}\end{array}.\right.\end{array}$$

Integrated along the longest flow path, the relationship between the catchment area and the width function can then be expressed as follows (Moussa, 2008):

$$\begin{array}{}\text{(7)}& \mathrm{area}=\underset{\mathrm{0}}{\overset{L_{\max }}{\int }}W\left(x\right)\mathrm{d}x.\end{array}$$

Therefore, for comparison among different catchments, the width function can be normalized as follows:

$$\begin{array}{}\text{(8)}& W^{\prime }\left(x^{\ast }\right)=W\left(x\right)/\mathrm{area},\text{ with }{x}^{\ast }=x/L_{max}.\end{array}$$

In this study, we develop the width function for each catchment based on the flow direction map from HydroSHEDS using the pysheds package in Python (https://github.com/mdbartos/pysheds, last access: 19 March 2024). Given the flow direction map, catchment delineation and river network extraction proceeded after the implementation of flow accumulation. The threshold of flow accumulation is set to be the 96th percentile of the total accumulation since it is an easy and efficient way compared with other more complex methods. (Passalacqua et al., 2010). Based on the derived river network, the flow distance of each DEM grid is computed, and the width function is estimated as the histogram of the catchment area (represented by the number of grids) against flow distance.

3.3 Width-function-based instantaneous unit hydrograph

The width function is closely related to the development of a geomorphic instantaneous unit hydrograph (Singh et al., 2014). The WF-based IUH (i.e., WFIUH) is the combination of the WF with any possible linear-routing scheme. If only the river network routing is taken into account, the convection–diffusion equation can be applied to calculate the WFIUH after stream network ordering (Franchini and O'Connell, 1996). The expression form of WFIUH becomes the following:

$$\begin{array}{}\text{(9)}& \mathrm{WFIUH}\left(t\right)=\underset{\mathrm{0}}{\overset{L_{max}}{\int }}{f}_x\left(t\right)W\left(x\right)\mathrm{d}x,\end{array}$$

where, f_x(t) represents the flow time distribution at the distance x along the river network in a watershed, and W(x) is the width function. L_max is the longest length of the stream network.

Equation (9) ignores hillslope routing within a catchment. The hillslope routing, however, could be a critical process in determining runoff response to rainfall and in shaping the IUH (Saco and Kumar, 2004). With the consideration of the effects of hillslope routing, it is proposed to combine the spatial distribution of flow velocity and the width function to derive WFIUH (Grimaldi et al., 2010), which is adopted in this study. Four approaches are commonly used to calculate flow velocity (Grimaldi et al., 2010), including Darcy–Weisbach's formula (Katz et al., 1995), Manning's formula, the Soil Conservation Service (SCS) formula (Haan et al., 1994) and the uniform-flow formula (Maidment et al., 1996). Making use of a remotely sensed land cover dataset, we herein adopt Manning's formula in our calculation, which is expressed as follows:

$$\begin{array}{}\text{(10)}& v={\displaystyle \frac{y^{\frac{\mathrm{2}}{\mathrm{3}}}\sqrt{S}}{n}},\end{array}$$

where n is Manning's roughness coefficient that is related to the land cover type of catchments (in m^−⅓ s).

To calculate the velocity, as shown in Fig. 2, a spatial map of the slope for each catchment is produced based on the DEM from SRTM. The 10 m FROM-GLC land cover data are then resampled to 90 m resolution to match with those of the DEM. Manning's roughness n for each 90 m grid was assigned according to the look-up table of land cover type against roughness (Table S1 in the Supplement).

4 Results

4.1 Spatial distribution of hydrogeomorphic characteristics

A total of 18 hydrogeomorphic metrics of 18 440 catchments across the Tibetan Plateau are provided in our dataset (TPHGD). Metrics of a small portion of catchments (< 1 %) are missing due to spatial mismatch or data quality. Figure 3 presents a statistical summary of the metrics, while Fig. 4 shows spatial patterns of the metrics across the Tibetan Plateau. As shown in Fig. 3, the area of the 18 440 catchments ranges between 4.8 and 216 km², with the perimeter varying from 9.8 to 132.7 km and the catchment mean elevation varying from 123.8 to 6180.9 m. Most of the catchments are located between 2200 and 6100 m. Catchments with higher elevations are in the western and central parts of the TP. Catchments in the western and southeast TP are steeper than other catchments in the TP. Catchment length and width are similar in their statistical distribution (Fig. 3), both largely between 1–30 km.

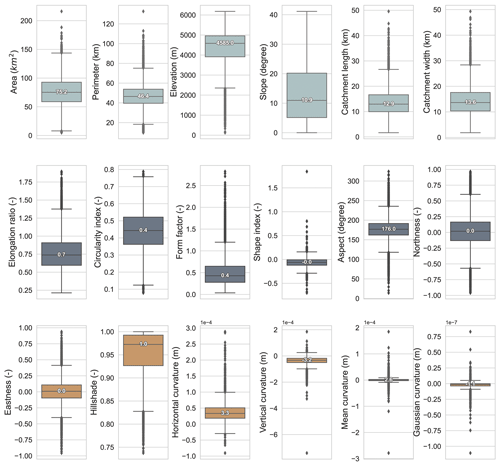
Figure 3 Statistical summaries of 18 hydrogeomorphic metrics for 18 440 catchments across the Tibetan Plateau.

Ranges of the elongation ratio, circularity index and form factor of the catchments are 0.2–1.9, 0.08–0.79 and 0.04–2.82, respectively. Around three-quarters of the catchments have an elongation ratio lower than 1, which means the majority of catchments tend to be elongated. Catchments in the central TP are more elongated (R_e>1.0) with a pinnate river network (R_f>1.0). Catchments located in the western and eastern TP are less elongated and more fan-shaped (Fig. 4). Most catchments show a concave hyperbolic land surface, with a shape index between −0.5 and 0, except for catchments located in the southeast TP. Most catchment aspects are between 150 and 200°, with their northness and eastness ranging between −0.25 to 0.25 and −0.5 to 0.5, respectively. This reveals that most catchments in the TP face southwest, south or southeast. The hillshade of most catchments is above 0.9 (Fig. 3). Catchments in the southeast TP have lower hillshade, suggesting that they are in the alpine and valley areas, with a higher shading effect. The curvature of a catchment affects the movement of water, sediment and biogeochemical matter. In addition to the horizontal and vertical curvatures, the Gaussian and mean curvatures for each catchment are recorded in our dataset as well. The median horizontal and vertical curvatures of all the TP catchments are around 0.33 × 10⁻³ and −0.32 × 10⁻³ m, respectively. Medians of mean and Gaussian curvature are 0.26 × 10⁻³ and −0.11 × 10⁻⁶ m, respectively. It is worth noting that the curvature metrics in our dataset represent those at a catchment scale, which are averages of each grid cell within the catchment. Hence, catchments with less curvature suggest a greater extent of flat or plain terrain within the catchment.

Figure 4 Spatial patterns of hydrogeomorphic metrics across the Tibetan Plateau.

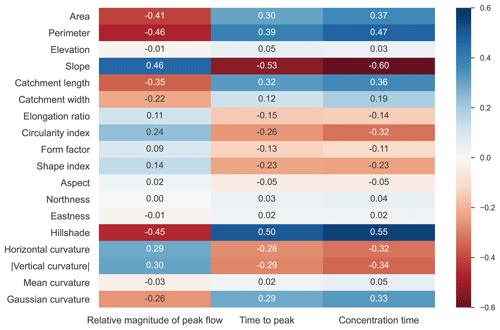
Figure 5 shows correlations among the 18 metrics. Catchment area (A_c) is found to be significantly correlated with catchment length (L_c), width (L_w) and perimeter (P_c) and could be represented by the power law (Fig. 5b, c, d). The relationship between A_c and L_c largely follows Hack's law (Rigon et al., 1996; Sassolas-Serrayet et al., 2018), which suggests a power law between the length of the river channel and the drainage area. The catchment perimeter is negatively correlated with the circularity index (with a correlation coefficient $r=-\mathrm{0.55}$). Elongation ratio, circularity index and form factor are highly related to catchment length, catchment width and perimeter, as can be expected according to Eqs. (2)–(4). The form factor and the elongation ratio are highly related (r=0.98). This may indicate that the elongation ratio and form index represent similar shape information of a catchment. The slope of the catchments is correlated negatively with hillshade ($r=-\mathrm{0.97}$), vertical curvature ($r=-\mathrm{0.49}$) and Gaussian curvature ($r=-\mathrm{0.53}$) but positively with shape index (r=0.36) and horizontal curvature (r=0.52). There is no significant correlation between catchment slope and elevation, with a correlation coefficient of no more than ±0.3.

Figure 5 Correlation between the 18 hydrogeomorphic metrics (a) and relationships between catchment area and catchment length, width and perimeter (b).

4.2 Classification of catchment width function

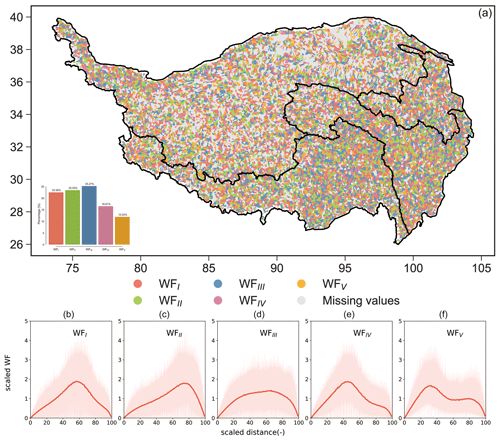
The width function of a catchment is a comprehensive curve reflecting the effects of landform on hydrological behavior and is used to develop the instantaneous unit hydrograph for catchments across the TP. In TPHGD, normalized width functions of 13 456 out of the 18 440 catchments are presented since it is less meaningful to derive the width function of a catchment with a relatively smaller area. The normalized width functions of the 13 456 catchments across the TP are grouped into five types by using the K-means unsupervised clustering approach and the gap statistic method.

The shapes of the five types of width functions are shown in Fig. 6. The first two types of width function both have a notable peak value in the curve (i.e., area proportion against distance to catchment outlet). However, the WF_I is peak-centered, while WF_II is peak-skewed. The shape of catchments characterized by these two types of width functions is typically elongated, with tributaries predominantly located in the upstream areas, resulting in relatively lengthy routing pathways. The third type of the width function (WF_III) is largely uniform-like without notable peaks. This width function type is often observed in catchments with larger overall areas or with a relatively consistent density of river networks extending from upstream to downstream. The fourth (WF_IV) and fifth (WF_V) types of width function are with dual peaks. The main difference between them is that the first peak in WF_IV is dominant, while the two peaks in WF_V are much closer in value. Catchments with WF_IV or WF_V are approximately parallel river systems, having more tributaries converging separately with catchment outlets than other catchments.

For the 13 456 catchments across the TP, the proportions of catchments with a specific width function type are 22.58 % (WF_I), 23.53 % (WF_II), 25.27 % (WF_III), 16.61 % (WF_IV) and 12.02 % (WF_V). As shown in Fig. 6, however, there is no clear spatial pattern in the width function across the TP. The spatial distribution characteristics of the width function are relatively random, and the obvious spatial aggregation characteristics of different classification width functions cannot be found in our dataset.

Figure 6 Typical width functions (b–f) and their spatial distribution across the Tibetan Plateau (a). At the bottom, the pink background indicates ranges of width function from the catchment subset of that type, while the red curve represents the median of the corresponding catchment subset.

4.3 WFIUH of catchments across the Tibetan Plateau

Based on the catchments' width functions, instantaneous unit hydrographs for each of the 13 456 catchments across the TP are derived and presented in the TPHGD dataset together with flow velocity estimated by Manning's approach for each grid cell. The time interval of the derived WFIUH is 30 min. There are some catchments located in the eastern continental basin whose WFIUH cannot be extracted due to large irrigation areas and canals. Herein, characteristics of the WFIUH indicated by peak flow magnitude (Q_p), time to peak (T_p) and concentration time (T_c, i.e., width of time base in WFIUH) for catchments across the TP are investigated. Their relationships with the 18 geomorphic metrics are also examined. The box plot of the relative magnitude of peak flow, time to peak and the total width of the WFIUH, as well as the spatial pattern of the three variables, is demonstrated in Fig. 7. This information can reveal the distribution features of the WFIUH of 13 456 catchments in the Tibetan Plateau, which may be valuable for flood risk decision-making and management in this region. As shown in Fig. 7, the relative magnitude of peak flow for most catchments ranges from 0.05 to 0.15, with the mean and median being 0.121 and 0.103, respectively. The smaller relative magnitude of the peak flow value represents a more uniform hydrograph distribution and a less obvious peak. The higher the Q_p, the more susceptible the catchment is to flash floods. Catchments with a higher Q_p are found in the northwestern or northern edge of the inland region (IR). Catchments in the central IR have relatively lower Q_p due to their smaller slopes. Catchments in the upper Yellow River basin (YLRB) and Yangtze River basin (YZRB) have correspondingly smaller Q_p than catchments in the lower YLRB and YZRB. Catchments in the southwest basin (SWB) have the highest Q_p as compared to catchments in the other three regions. Particularly, in the Nu River, Jinsha River, Lancang River and the Palong Zangbo area, Q_p can reach 0.2 and above, which explains well the high flood risks in those regions. In the middle and lower reaches of the Yarlung Zangbo River and the Shiquan River areas, the relative magnitude of peak flow is also higher than that of the whole Tibetan Plateau.

The time to peak in most catchments mainly ranges from 2 to 15 h, with mean and median T_p around 10.3 and 9.0 h, respectively. The spatial distribution of T_p across the Tibetan Plateau is similar to that of Q_p, suggesting that the shorter the T_p is, the higher the Q_p is. Catchment concentration time, however, varies from 10 to 35 h, with mean and median T_c around 18.3 and 16.5 h, respectively. Catchments with longer T_c are found in the central TP and YLRB. Catchments in the northwest IR and in the middle and lower reaches of the Yarlung Zangbo River, Palong Zangbo River and Nu-Jinsha-Lancang basins all have relatively short T_c (< 20 h). Regions that have high Q_p but short T_p and T_c are usually characterized by elongated catchments, a pinnate river network, higher slopes, and lower roughness.

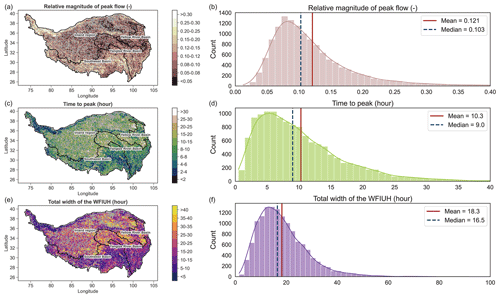
Figure 7 Distribution of WFIUH characteristics across the Tibetan Plateau. (a, c, e) Spatial distribution and (b, d, f) statistical distribution represented by histogram.

Figure 8 further shows the relationships of Q_p, T_p and T_c with the 18 hydrogeomorphic metrics in our TPHGD dataset. It is found that Q_p is positively related to slope, horizontal curvature and absolute vertical curvature. Q_p is negatively related to catchment area, perimeter, length and circularity. The relationships of T_p with the hydrogeomorphic metrics are similar to those of Q_p but in an oppositive direction. This suggests that a catchment with a larger, more circular shape may exhibit a more gradual rising limb in its hydrograph. T_c has a strong negative correlation with catchment slope as a steeper land surface can result in faster flow, hence shortening the traveling time of water flow. Unsurprisingly, T_c is positively related to catchment size, defined by area, perimeter and length.

Figure 8 Correlations between WFIUH characteristics and 18 hydrogeomorphic metrics.

4.4 Validity and uncertainty of derived WFIUH

The derived WFIUH in our TPHGD dataset is expected to represent the hydrological response function in a catchment, contributing in particular to generating a hydrograph of ungauged catchments in the Tibetan Plateau. To examine the validity, we have incorporated the derived WFIUH into a conceptual hydrological model, GR4H (Perrin et al., 2003). GR4H is a model with four parameters running at an hourly time step. The fourth parameter of GR4H (x4) represents the time base of a hypothetical unit hydrograph. In this study, the hypothetical unit hydrograph is replaced by our derived WFIUH, and the parameter x4 is then removed. The model was tested at four gauged catchments in the Tibetan Plateau for 48 flash-flood events from 2008 to 2016. The required inputs of the model (rainfall and potential evapotranspiration) and the observed hourly streamflow data are obtained from China's Annual Hydrological Report.

Overall, the model performs well for most of the flash-flood events as evaluated by NSE (Nash and Sutcliffe, 1970), bias in peak flow (BS_qp) and bias in time to peak (BS_tp) (Fig. 9). The simulated hydrograph is compared to the observed one for selected catchments and is shown in Fig. 9 as well. As shown in Fig. 9, the median NSE of the 48 flash events is around 0.67 for more than 50 % of the 48 flash-flood events, with an absolute value of BS_qp lower than 10 % and an absolute value of BS_tp lower than 3 h. Peak flows of 26 flood events are underestimated, while those of the other 22 events are overestimated, suggesting no systematic tendency in the modeling. The time to peak (T_p) of about two-thirds of simulated flood events lags behind the observed one, indicating uncertainties in the simulations.

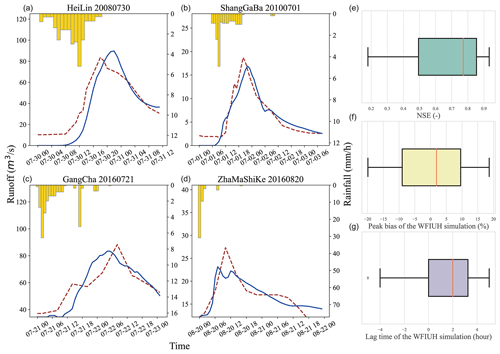
Figure 9 Performance of hydrological modeling by incorporating WFIUH into GR4H model. (a–d) Comparison between simulated and observed hydrograph for flash events at different catchments (dashed red curve is observed, solid blue curve is simulated) and (e, f, g) summary of overall model performance for 48 simulated flash-flood events.

Table 2 Files in the TPHGD dataset.

Uncertainties in the simulations cannot only be due to the uncertainties in the derived WFIUH but must also be due to uncertainties in model structure, model inputs and model parameters. In terms of WFIUH, its validity could be affected by the spatial resolution and sources of the DEM and the effectiveness of the method in estimating flow velocity. In this study, the DEM dataset from SRTM is used, which has a spatial resolution of 90 m. We find it challenging to derive WFIUH for catchments with relatively small areas and with highly complicated topography using the DEM from SRTM. Hence, a DEM with a higher spatial resolution can be conducive to improving the derivation of WFIUH for those catchments. It is worth noting that the uncertainties in WFIUH could be considerably affected by the estimate of flow velocity. In this study, Manning's approach is used to calculate flow velocity at each grid cell and then works with the catchment's width function to derive the WFIUH. Other approaches such as the Darcy–Weisbach formula (Katz et al., 1995), the Soil Conservation Service (SCS) formula (Haan et al., 1994) and the Maidment et al. (1996) uniform flow equation may result in a different estimate of flow velocity and hence of the subsequent WFIUH. In addition, the roughness coefficient in Manning's approach assigned for each grid cell is affected by the accuracy of the land cover map, leading to uncertainties in the estimated flow velocity. It has been reported that a higher deviation in the roughness coefficient could result in a higher deviation of the hydrograph peaks (Kalyanapu et al., 2009). Thus, a detailed evaluation of Manning's roughness in different land cover types using remote sensing skills is needed to reduce the uncertainties (Mtamba et al., 2015; Sadeh et al., 2018). For further exploration of the uncertainties in the future, in this version of the dataset, we also provide the width function for each catchment, which facilitates the derivation of WFIUH given different estimates of flow velocity.

5 Code and data availability

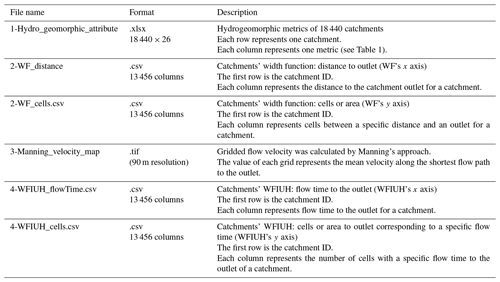
Our TPHGD dataset provides 18 hydrogeomorphic metrics for 18 440 catchments across the Tibetan Plateau together with the width function and WFIUH of 13 456 out of the 18 440 catchments. Table 2 lists the structure of the dataset and the formats of the files there. The 18 metrics of all catchments are presented in an Excel file. The catchment's width function is stored in two separate CSV files, one of which represents the distance to the catchment outlet (i.e., x axis in the WF plot), while the other represents the number of cells (equivalent to counts and represented by the y axis in the WF plot) at a given distance to the outlet. The gridded flow velocity map is presented as a tif file in Manning_velocity_map. Similarly to the catchment's WF, the WFIUH for each catchment is presented in two paired CSV files, WFIUH_flowtime.csv and WFIUH_cells.csv. The former provides flow time at a specific distance to the catchment outlet (i.e., the x axis in the WFIUH plot), while the latter provides the number of cells (equivalent to counts and represented by the y axis in the WFIUH plot) within the corresponding distance. The dataset is archived at and is openly accessible via the Zenodo portal: https://doi.org/10.5281/zenodo.8280786 (Guo and Zheng, 2023).

The Python scripts used for deriving WFIUH, curve fitting and classification are freely available at https://doi.org/10.5281/zenodo.10836824 (Guo, 2024). The dependency Python package (pysheds) used in deriving catchment WF is available at https://github.com/mdbartos/pysheds (Bartos, 2020).

6 Conclusions

The Tibetan Plateau provides an ideal setting for investigating the hydrological and geomorphic interactions between hydrological and geomorphic processes in a largely pristine natural environment, minimally impacted by human activities. The hydrological behaviors of catchments across the Tibetan Plateau, however, remain largely unknown due to its challenging physical conditions and data limitations. This study presents the inaugural version of a hydrogeomorphic dataset encompassing 18 440 catchments across the region. The dataset comprises 18 hydrogeomorphic metrics along with, in particular, the width function and width-function-based instantaneous unit hydrograph of each catchment. It can contribute to advancing our understanding of catchment hydrological behaviors in the Tibetan Plateau and hence improving water resources management and disaster mitigation in the region and its downstream areas. Particularly, the newly derived WFIUH can be conducive to flash-flood modeling in catchments with few hydrological observations.

According to the dataset provided, it is found that catchments with higher elevation are in the western and central parts of the TP, while catchments in the western and southeast TP are steeper than other catchments in the TP. Catchments in the central TP are more elongated, with a pinnate river network, and catchments in the western and eastern TP are less elongated and more fan-shaped. A power relationship (i.e., Hack's law) exists between catchment area and length. We also find that the peak flow of WFIUH is positively related to slope and curvature but negatively related to catchment area, perimeter, length and circularity. The relationships of time to peak with the hydrogeomorphic metrics are similar to those of peak flow but in an oppositive direction. Catchment concentration time shows a positive relationship with catchment size but a strong negative correlation with catchment slope as a steeper land surface can result in faster flow and, hence, a shortening of the traveling time of water flow.

The validity of the derived WFIUH has been confirmed by its successful integration into an hourly hydrological model for simulating flash-flood events. Uncertainties in the simulation may arise from factors such as model structure, model inputs, model parameterization and the derived WFIUH. Particularly, uncertainties in the WFIUH can be attributed to the resolution of the DEM and the methods employed for calculating flow velocity. These aspects warrant further exploration in future research endeavors.